Scarica

CBM a.s. 2012/2013
MATEMATICA ed ECONOMIA
Legge della domanda:
q = f(p)
Le variabili utilizzate sono:
q quantità richiesta di un bene (i cui valori vengono riportati sull’asse verticale)
p prezzo unitario
(i cui valori vengono riportati sull’asse orizzontale)
Attraverso rilevazioni statistiche si trovano vari tipi di funzioni di domanda q (si usa anche la
variabile d al posto di q), che sono sempre funzioni decrescenti del prezzo.
Alcuni esempi di funzione di domanda possono essere (i parametri a e b non sono mai numeri
negativi):
Lineare: q a bp ;
Parabolica: q
Iperbolica: q
Esponenziale: q
a
q
p
a bp 2 ;
a
c;
p b
a e
bp
;
L’inversa della funzione domanda è la funzione del prezzo, anch’essa decrescente, che si ottiene
q
ricavando p in funzione di q (ad es. se q 80 4 p si può ricavare p 20
).
4
Indicando con :
p p 2 p 1 la variazione assoluta del prezzo;
q
q2
p 2 p1
p1
q 2 q1
q1
q 1 la variazione assoluta della domanda;
la variazione relativa del prezzo;
la variazione relativa della domanda;
si definisce coefficiente di elasticità della domanda il numero positivo e
q
q q1 p1
q1
q p1
e= 2
p
p 2 p1 q1
p q1
p1
Esso permette di valutare come il mercato reagisce alla variazione di prezzo di un determinato bene.
Il coefficiente di elasticità ora definito si chiama anche elasticità d’arco perché misura l’elasticità
media (cioè l’elasticità del punto medio della corda che unisce i punti A(p1;q1) e B(p2;q2) che stanno
sul grafico della funzione di domanda q = f(p)) ed è un’approssimazione del valore esatto
dell’elasticità dei punti della curva di domanda compresi fra A e B.
Possiamo avere tre casi:
1
CBM a.s. 2012/2013
e>1
domanda elastica, in cui la variazione relativa della domanda è maggiore della
variazione del prezzo (è il caso dei beni voluttuari);
domanda anelastica;
domanda rigida (è il caso dei beni di prima necessità).
e=1
e<1
Gli elementi fondamentali che determinano l’elasticità di una domanda rispetto al prezzo sono:
- esistenza di sostituti: più ci sono buone alternative al prodotto, maggiore è l’elasticità;
- natura del bisogno:i beni di lusso hanno generalmente una domanda elastica rispetto al
prezzo, i beni di prima necessità hanno generalmente una domanda anelastica rispetto al
prezzo;
- il periodo di tempo: nel lungo periodo la domanda è in genere più elastica;
- il numero degli usi: maggiore è il numero di usi per cui il prodotto può essere destinato,
maggiore sarà la sua elasticità di prezzo;
- la quota di reddito spesa per quel prodotto.
Se la legge della domanda q = f(p) è espressa da una funzione continua e derivabile è possibile
considerare l’elasticità puntuale della domanda in un punto p (se q≠0 in quel punto), definita
p '
p 1 , cioè quando p 0 ; anch’essa si indica con e =
quando p 2
f ( p) .
q
Legge dell’offerta:
q = f(p)
Utilizziamo le grandezze p e q come in precedenza, ma q indica la quantità di un bene offerta sul
mercato. Si hanno diverse leggi dell’offerta, funzioni crescenti o non decrescenti, come ad
esempio(i parametri a e b non sono mai numeri negativi):
:
a bp ;
lineare q
q a bp ;
q
a
p b.
L’inversa della funzione di offerta (che si ottiene se si ricava p in funzione di q) si chiama
funzione di produzione.
Si può calcolare il coefficiente di elasticità dell’offerta seguendo lo stesso procedimento di quello
della domanda.
Equilibrio tra domanda e offerta
Il Mercato può configurarsi secondo tre regimi: Monopolio, Oligopolio e Concorrenza perfetta.
Monopolio: esiste una sola impresa in grado di produrre una determinata merce o di fornire un
servizio che non possono essere sostituiti da altre merci o servizi;la conseguenza sul mercato è
2
CBM a.s. 2012/2013
la mancanza di concorrenza e la possibilità per chi produce di fissare il prezzo di vendita a
propria discrezione.
Oligopolio:ci sono poche imprese in grado di produrre una determinata merce o di fornire un
servizio che non possono essere sostituiti da altre merci o servizi; le conseguenze sul mercato
sono simili a quelle determinate dal monopolio
Concorrenza perfetta: sul mercato di un prodotto opera un grande numero di imprese e di
compratori; in media, le imprese sono piccole; compratori e venditori conoscono perfettamente
tutte le transazioni del mercato; le conseguenze sul mercato sono che nessuno può influenzare il
mercatoimponendo le condizioni (prezzi, quantità scambiate,…) in cui avviene lo scambio di
beni e servizi che verrebbero prodotti al massimo dell'efficienza e cioè al prezzo e al costo più
bassi, e i consumatori otterrebbero la quantità massima di beni e servizi.
In condizioni di concorrenza perfetta, conoscendo le leggi della domanda e dell’offerta è possibile
determinare il prezzo di equilibrio (che è il prezzo per cui la quantità domandata è uguale alla
quantità offerta), con la corrispondente quantità domandata e offerta.
Per via analitica, tale prezzo si determina risolvendo l’equazione f ( p ) f * ( p ) dove d f ( p) è la
funzione di domanda e q f * ( p ) è la funzione di offerta e p è il prezzo.
Di questo problema è possibile fornire una rappresentazione grafica, e il prezzo di equilibrio è
l’ascissa del punto di intersezione delle curve grafico della funzione di offerta e della funzione di
domanda.
Costi di produzione
Si chiamano costi fissi i costi indipendenti dalla quantità prodotta.
Si chiamano costi variabili i costi che variano al variare della quantità prodotta (crescono
all’aumentare della quantità prodotta)
Si chiamano costi totali la somma fra i costi fissi e i costi variabili.
La funzione del costo totale, sempre crescente, è y Ctot (x) dove con y indichiamo il costo e con x
la quantità di merce prodotta, dove x≥0.
Ponendo x
0 si ottengono i costi fissi Cf = Ctot (0) .
Si possono presentare i seguenti tipi di funzioni di costo più diffuse:
 lineare y ax b ;


parabolica y ax 2 bx c (di cui si considera il ramo crescente);
esponenziale y ke x .
C ( x)
, x 0 , se si tiene conto
Definiamo la funzione costo medio(o costo unitario) come C m ( x)
x
C( x 2 ) C( x1 )
della totalità della merce prodotta, oppure come C m
se si fa riferimento al
x 2 x1
passaggio dalla produzione x 1 alla produzione x 2 .
Il punto di, minimo della funzione Costo unitario viene chiamato Punto di fuga in quanto se il
prezzo di vendita unitario del bene fosse inferiore al costo minimo unitario (Valore assunto nel
Punto di fuga) l’impresa sarebbe in perdita e dovrebbe andarsene dal mercato.
3
CBM a.s. 2012/2013
Col termine costo marginale unitario intendiamo il costo relativo ad una unità addizionale di
prodotto ed è definito dalla funzione Cm a ( x) C ( x 1) C ( x) .
Con il termine costo marginale si intende, quando esiste, la funzione derivata prima del costo totale
'
C ma ( x) Ctot
( x) .
Ricavi e utili di produzione
Nel caso di libera concorrenza (in cui il prezzo di vendita non dipende dalla quantità venduta,
perché l’impresa non ha potere d’influire sul prezzo, e il prezzo è per lei un dato) abbiamo che il
ricavo dalla vendita di una quantità x di merce è rappresentato dalla funzione R( x) p x ; in
regime di monopolio (in cui il prezzo di vendita è funzione della quantità venduta, perché l’impresa
ha un certo potere di mercato e sa che, per esempio, diminuendo il prezzo venderà più beni)
p f (x) , quindi R( x) f ( x) x .
Ricavo marginale: E’ la derivata prima del ricavo totale, cioè R' ( x) .
Utile (Profitto, Guadagno): E’ rappresentato dalla funzione U ( x)
( x)
G ( x)
R( x ) C ( x ) .
Per determinare la quantità x di merce prodotta (e quindi venduta) che consente di non essere in
perdita occorre trovare quei valori di x≥0 per cui U (x) 0 , cioè R( x) C ( x) 0 .
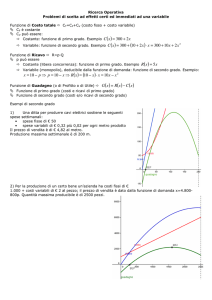
Chiamiamo Diagramma di Redditività la rappresentazione grafica su uno stesso piano cartesiano
delle funzioni di Costo, della funzione di Ricavo e dei Vincoli.
Un Punto di pareggio o BREAK EVEN POINT (abbreviato in B.E.P.) o Punto di equilibrio
economico è un punto di intersezione fra la funzione dei Costi totali e quella dei Ricavi.
Tale punto separa graficamente l’Area di Perdita (formata dai punti del piano compresi fra la
funzione dei Ricavi e quella dei Costi quando i ricavi sono minori dei costi) dall’Area di Guadagno
(formata dai punti del piano compresi fra la funzione dei Ricavi e quella dei Costi quando i ricavi
sono maggiori dei costi) e rappresenta quindi un punto in cui il guadagno è nullo.
La quantità di beni da produrre e vendere che ci consente di non lavorare in perdita si ottiene
trovando i valori x≥0 per cui U(x) ≥ 0.
I valori x≥0 per cui U(x) = 0 sono i valori della x dei B.E.P.
4