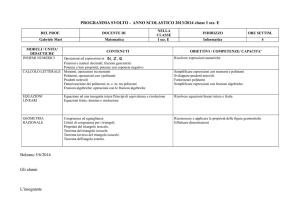
IISS PIETRO VERRI
PROGRAMMA DI MATEMATICA
CLASSE I F
Anno scolastico 2012/13
Docente prof. Maurizio Di Vasto
Aritmetica e algebra
Conoscenze
Abilità
1. NUMERI NATURALI
Divisibilità e scomposizione in fattori primi.
Massimo comun divisore e minimo comune
multiplo. Operazione di addizione e
moltiplicazione e loro proprietà. Potenze e loro
proprietà.
Saper scomporre un numero in fattori primi.
Saper determinare il massimo comun divisore e
il minimo comune multiplo di un insieme di
numeri.
Saper eseguire le operazioni tra numeri.
Saper applicare le proprietà delle operazioni.
2. NUMERI RAZIONALI
Frazioni e loro proprietà. Operazioni tra
frazioni. Confronto tra frazioni. Frazione
generatrice di un numero decimale. Proporzioni.
Saper operare con le frazioni.
Saper trasformare in frazione un numero
decimale.
3. NUMERI RELATIVI
Numeri interi. Operazioni con i numeri interi.
Numeri razionali relativi. Potenze ad esponente
negativo.
Saper operare con i numeri relativi.
4. NUMERI REALI
La rappresentazione sulla retta dei numeri reali.
5. CALCOLO LETTERALE
Monomi. Monomi simili. Monomi opposti.
Grado di un monomio. Operazioni con i
monomi: somma e differenza di monomi;
somma algebrica di monomi simili; prodotto di
monomi; potenza di un monomio; divisione di
due monomi; MCD e mcm di due o più
monomi. Polinomi: grado di un polinomio;
polinomi ordinati; polinomi completi.
Operazioni con i polinomi: prodotto di un
monomio per un polinomio; quoziente tra un
polinomio e un monomio; prodotto di polinomi.
Prodotti notevoli: quadrato di un binomio;
quadrato di un trinomio; prodotto della somma
di due monomi per la loro differenza; cubo di un
binomio; triangolo di Tartaglia; potenza di un
binomio. Divisione tra polinomi. Teorema del
resto. Regola di Ruffini. Scomposizione in
fattori di un polinomio: raccoglimento totale a
fattore comune; raccoglimento parziale a fattore
comune; trinomio scomponibile nel quadrato di
un binomio; scomposizione della differenza di
due quadrati; quadrinomio scomponibile nel
cubo di un binomio; scomposizione della
somma e della differenza di due cubi;
scomposizione del trinomio notevole;
scomposizione mediante la regola di Ruffini.
Saper operare con i polinomi
Saper applicare le regole dei prodotti notevoli
Saper scomporre un polinomio in fattori.
Saper semplificare una frazione algebrica.
Saper operare con le frazioni algebriche.
MCD e mcm di polinomi. Frazioni algebriche:
condizione di esistenza di una frazione
algebrica; frazioni equivalenti; proprietà
invariantiva delle frazioni algebriche;
Semplificazione delle frazioni algebriche;
riduzione di frazioni algebriche allo stesso
denominatore. Operazioni con le frazioni
algebriche: somma algebrica di frazioni
algebriche; prodotto di frazioni algebriche;
quoziente di frazioni algebriche; potenza di una
frazione algebrica.
6. EQUAZIONI DI I GRADO
Equazioni di I grado intere e numeriche
Saper risolvere un’equazione di I grado
Geometria
1. I PRIMI ELEMENTI
Termini primitivi. Assiomi e teoremi. Semirette,
segmenti e angoli. Il concetto di congruenza.
2. I TRIANGOLI
Spezzate e poligoni. La congruenza dei
triangoli. I tre criteri di congruenza. Proprietà
del triangolo isoscele; teorema della congruenza
degli angoli adiacenti alla base in un triangolo
isoscele.
Saper dimostrare il terzo criterio di congruenza
(LLL).
Saper dimostrare il teorema della congruenza
degli angoli adiacenti alla base in un triangolo
isoscele.
3. PARALLELISMO E PERPENDICOLARITÀ NEL PIANO
Rette perpendicolari. Teorema sulla bisettrice
dell’angolo al vertice in un triangolo isoscele
che è anche altezza e mediana. Teorema sulla
assenza di punti in comune tra due rette
perpendicolari a una stessa retta. Rette parallele.
Teoremi sul parallelismo di due rette tagliate da
una trasversale e relativi teoremi inversi.
Saper dimostrare il teorema sulla bisettrice
dell’angolo al vertice in un triangolo isoscele
che è anche altezza e mediana.
Saper dimostrare il teorema sulla assenza di
punti in comune tra due rette perpendicolari a
una stessa retta.
Milano, 8 giugno 2013
PROF. MAURIZIO DI VASTO
firmato Maurizio Di Vasto
GLI STUDENTI
firmato Liam Delle Piane
Sergest Islamaj
John Nicolas Helera