In un condensatore Q = C V Se V varia nel tempo v(t) i(t) = C dv(t)/dt

In un condensatore Q = C V
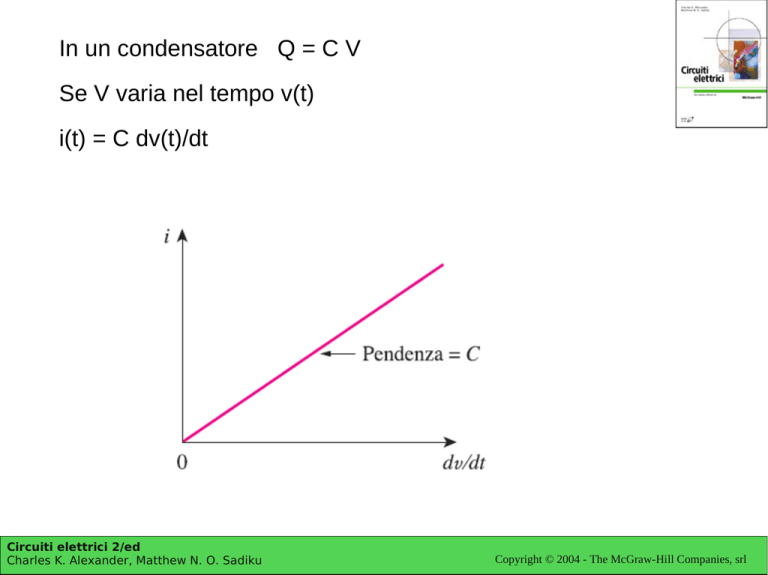
Se V varia nel tempo v(t)
i(t) = C dv(t)/dt
Circuiti elettrici 2/ed
Charles K. Alexander, Matthew N. O. Sadiku
Copyright © 2004 - The McGraw-Hill Companies, srl
Circuiti elettrici 2/ed
Charles K. Alexander, Matthew N. O. Sadiku
Copyright © 2004 - The McGraw-Hill Companies, srl
Ricordiamo che
V = E d = q /C = q / ( ε0 A/d)
L'incremento di energia durante la
carica di un condensatore
dU =dL =V dQ =( Q/C ) dQ
U=Ltot =
∫0
Qmax
(q/C) dQ =1/2 Qmax2/C = 1/2 C Vmax2
q(V)
L
V
L'energia immagazzinata in un condensatore di capacita' C pari a
C = ε A/d
Dopo essere stato caricato alla tensione V vale
U = ½ C·V2 = ½ (ε A/d)·V2 = ½ ε ·(A/d) · ( E·d )2 = ½ ε ( A·d ) E 2
Ma A·d e' il volume Vol del condensatore ( in m3)
Energia Uvol in un condensatore per unita' di volume ( Joule / m3)
Uvol = ½ ε E
2
L’energia nel condensatore considerato è immagazzinata
tra le armature conduttrici.
Si puo' dimostrare che tale espressione e' valida
anche per campi elettrici non omogenei
Attenzione: non toccate i condensatori senza esservi accertati
che sono stati scaricati !
U= 1/2 C V2
Si
No
La energia non puo' variare istantaneamente ( richiederebbe una
potenza infinita!)
QUINDI
La tensione ai capi di una capacita' deve essere continua nel tempo
Circuiti elettrici 2/ed
Charles K. Alexander, Matthew N. O. Sadiku
Copyright © 2004 - The McGraw-Hill Companies, srl