APPUNTI DI
CIRCUITI ELETTRONICI DIGITALI
Aprile - Giugno 2009
Appunti di elettronica digitale tratti dalle lezioni del corso di Circuiti Elettronici
Digitali L-A alla facoltà di Ingegneria Elettronica dell’Università di Bologna tenute
dal professor B. Riccò e raccolti da Francesco Conti
INDICE DEI CONTENUTI
Transistori MOS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Struttura del transistore MOS . . . . . . . . . . . . . . . . . . .
Caratteristiche statiche del transistore MOS . . . . . . . . . . .
Modello alle variazioni a bassa frequenza del transistore MOS
Funzionamento ad alta frequenza del transistore MOS . . . . .
Logica FCMOS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Invertitore CMOS statico . . . . . . . . . . . . . . . . . . . . . .
Buffer e tri-state . . . . . . . . . . . . . . . . . . . . . . . . . . .
Gate FCMOS . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Logiche non FCMOS . . . . . . . . . . . . . . . . . . . . . . . . . . .
Pass transistor e transfer gate . . . . . . . . . . . . . . . . . . .
Multiplexer a pass transistor . . . . . . . . . . . . . . . . . . . .
Circuiti domino . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ripartizione di carica nei circuiti dinamici . . . . . . . . . . . .
Circuiti sincroni . . . . . . . . . . . . . . . . . . . . . . . . . . .
Multivibratori . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Multivibratori bistabili . . . . . . . . . . . . . . . . . . . . . . .
Multivibratori monostabili . . . . . . . . . . . . . . . . . . . . .
Multivibratori astabili . . . . . . . . . . . . . . . . . . . . . . . .
Licenza . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4
4
5
7
9
12
12
17
18
20
20
21
22
23
24
25
25
27
28
30
INDICE DELLE FORMULE
(1) Capacità del canale per unità di area . . . . . . . . . . . . . . . . . . .
(2) Conducibilità estrinseca . . . . . . . . . . . . . . . . . . . . . . . . . .
(3) Conducibilità intrinseca . . . . . . . . . . . . . . . . . . . . . . . . . .
(4) Modello analitico del transistore NMOS . . . . . . . . . . . . . . . . .
(5) Tensione di soglia con effetto Body . . . . . . . . . . . . . . . . . . . .
(6) Transconduttanza gm . . . . . . . . . . . . . . . . . . . . . . . . . . .
(7) Conduttanza g0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(8) Transconduttanza di bulk αgm . . . . . . . . . . . . . . . . . . . . . .
(9) Corrente alle variazioni . . . . . . . . . . . . . . . . . . . . . . . . . .
(10) Tensione di overdrive . . . . . . . . . . . . . . . . . . . . . . . . . . .
(11) Soglia logica dell’invertitore CMOS . . . . . . . . . . . . . . . . . . .
(12) Fattori di forma nell’invertitore CMOS simmetrico . . . . . . . . . . .
(13) Fattori di forma nell’invertitore CMOS simmetrico ad area minima .
(14) Ritardo di propagazione dell’invertitore CMOS simmetrico . . . . .
(15) Formule di Elmore . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(16) Capacità d’ingresso di un gate CMOS . . . . . . . . . . . . . . . . . .
(17) Tempo di propagazione 10% − 90% con il metodo della resistenza
equivalente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(18) Tempo di propagazione 50% con il metodo della resistenza equivalente
(19) Dimensionamento del transistor con il metodo della resistenza
equivalente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(20) Buffer di massima efficienza . . . . . . . . . . . . . . . . . . . . . . . .
(21) Buffer con N invertitori . . . . . . . . . . . . . . . . . . . . . . . . . .
(22) Fattore di forma equivalente di una serie di n transistor . . . . . . . .
(23) Ripartizione di carica . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(24) Durata dell’impulso di un multivibratore monostabile . . . . . . . .
2
6
6
6
7
7
9
9
9
9
12
14
14
14
15
16
16
16
16
16
17
17
19
24
28
(25) Tempo di recupero di un multivibratore monostabile . . . . . . . . .
(26) Durata del segnale basso nell’astabile . . . . . . . . . . . . . . . . . .
(27) Durata del segnale alto nell’astabile . . . . . . . . . . . . . . . . . . .
3
28
29
29
TRANSISTORI MOS
Struttura del transistore MOS
Il transistore più diffuso in elettronica digitale è il MOSFET, ovvero Metal-OxideSemiconductor Field Effect Transistor, più comunemente detto transistore
MOS. Il fatto che il MOS sia a effetto di campo significa che esso è controllato
per mezzo di un campo elettrico, ovvero in tensione: sul terminale di controllo
non passa corrente di conduzione.
La struttura del transistore MOS è fondamentalmente quella di un condensatore non lineare in cui una delle armature è un conduttore (metal), in mezzo
c’è un dielettrico (oxide) e l’altra faccia è un semiconduttore (semiconductor). Il
campo elettrico che si forma in questo condensatore controlla la quantità di carica
in una regione detta canale, attraverso cui può quindi scorrere una corrente
controllata.
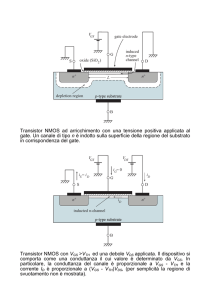
Figura 1: Schema di principio di un transistore NMOS
I transistori MOS si dividono in:
• n-channel o NMOS, in cui i portatori di carica nel canale sono elettroni
(negativi);
4
• p-channel o PMOS, in cui i portatori di carica nel canale sono lacune
(positive, si muovono più lentamente degli elettroni).
Inoltre, a seconda che il transistore funzioni inserendo carica nel canale o togliendone, è detto rispettivamente ad enhancement (arricchimento) o a depletion
(svuotamento). Il 90% dei transistor è del tipo enhancement.
Dal punto di vista circuitale, il MOS è un dispositivo a quattro morsetti: quello
di controllo è detto gate, quello da cui proviene la corrente (nel NMOS) è detto
drain, quello da cui esce è detto source e poi c’è un quarto terminale detto bulk o
body che costituisce il substrato su cui è costruito il transistore. Il bulk è formato
da un monocristallo di silicio debolmente drogato di tipo p, source e drain sono
invece in contatto con zone di silicio fortemente drogate di tipo n.
Il transistore MOS è controllato dalle tre tensioni VGS , VDS e VSB che nel
NMOS sono tutte positive. Le giunzioni SB, DB sono diodi in inversa e dunque
non conducono (se non una corrente piccolissima), per cui l’unica corrente
significativa è IDS . Il PMOS è simmetrico in tutto al NMOS: le sue tensioni sono
tutte negative e in esso la corrente scorre da source a drain, ma per il resto
funziona in modo assolutamente identico.
Figura 2: Schema circuitale di un transistore NMOS
Caratteristiche statiche del transistore MOS
Si può disegnare la transcaratteristica IDS (VGS ) tenendo costanti VSB = 0 e
VDS ≈ 100mV. Una VDS nulla annullerebbe ogni differenza fra source e drain
non permettendo lo scorrimento di corrento nel canale e spegnendo il transistore
(se invece fosse negativa, source e drain si scambierebbero poiché il transistore
MOS è simmetrico).
Dal grafico di IDS (VGS ) si può approssimativamente dedurre una tensione
di soglia VT (di solito circa 0.6V) prima della quale il transistore è spento e dopo
5
la quale si comporta approssimativamente come un resistore. Questa tensione
di soglia è un parametro determinato durante la produzione a partire da una
corrente minima considerabile significativa. In ogni caso essa non può essere né
troppo piccola (renderebbe il transistore difficile da spegnere) né troppo grande.
Variando VSB , si osserva una traslazione verso destra del diagramma, ovvero
un aumento della soglia. Questo effetto è detto effetto body.
L’altra caratteristica interessante del transistore MOS è IDS (VDS ), che è molto
simile a quella di un transistore bipolare (tranne per il fatto che le correnti in
gioco sono molto più piccole) ed è suddivisa in due regioni: una zona triodo
dove IDS dipende da VGS (nella prima parte, in cui la dipendenza è abbastanza
lineare, la zona è detta anche zona lineare) e una zona di saturazione dove la
dipendenza è estremamente limitata.
Nell’approssimazione che i transistori siano a canale lungo (non più valida per i transistori sub-micrometrici presenti nei moderni microprocessori), è
possibile derivare dal funzionamento fisico teorico del transistore NMOS un
modello analitico statico ai grandi segnali del transistore NMOS. Si introduce
l’approssimazione di canale graduale: che il canale sia costituito da uno strato di
carica appoggiato all’ossido in cui gli elettroni si spostano per via di un campo
elettrico trasversale E⊥ e uno longitudinale Ek considerabili separatamente. Il
campo E⊥ è dovuto, in questa approssimazione, alla tensione VGS e determina
come in un condensatore la quantità di carica presente nel canale; il campo Ek ,
dipendente da VDS , mette in moto le cariche del canale. Il moto delle cariche
è approssimato come ohmico, ovvero a velocità costante vdrift : anche questa
approssimazione decade con i campi intensi presenti nei transistori odierni.
Si definisce la capacità del canale per unità di area come
Cox =
εox
tox
(1)
dove tox è lo spessore dell’ossido e εox la sua costante dielettrica. Definita la
mobilità degli elettroni µn , si può definire la conducibilità estrinseca
β = µn Cox
W
L
(2)
e la conducibilità intrinseca
0
β = µn Cox
Il modello analitico del transistore NMOS è dunque dato da
6
(3)
• Spento (VGS < VT ):
IDS = 0
• Saturazione (VGS − VT < VDS ):
2
1 0 W VGS − VT (1 + λVDS )
IDS = β
2
L
(4)
• Triodo (VGS − VT > VDS ):
W
1 2
0
IDS = β
(VGS − VT )VDS − VDS
L
2
• Lineare (zona triodo con VDS → 0):
W
0
[VGS − VT ] VDS
IDS = β
L
La leggera di pendenza da VDS in zona di saturazione (regolata da un
parametro λ) è dovuta al fenomeno della modulazione di larghezza di canale.
La tensione di soglia VT è calcolabile in base ad un parametro VT 0 e all’effetto
Body:
hp
i
p
VT = VT 0 + γ
VSB + 2ΦF − 2ΦF
(5)
dove ΦF è un parametro senza particolare significato fisico nei transistor
odierni (in origine era il potenziale di Fermi).
In pratica il transistore si comporta come un circuito aperto se spento, come
un resistore controllato in tensione (dal condensatore gate-bulk) in regione lineare
e come un generatore di corrente dipendente in regione di saturazione.
Modello alle variazioni a bassa frequenza del transistore MOS
Per il transistore MOS si può derivare da questo modello un modello equivalente
alle variazioni a bassa frequenza: in esso compaiono una transconduttanza gm
W
0
gm = β
VDS
(in zona triodo)
L
p
(in zona di saturazione)
(6)
gm = β(VGS − VT ) = 2βIDS
7
Figura 3: Caratteristiche IDS (VGS ) e IDS (VGS ) di un NMOS senza modulazione di
larghezza di canale
8
una conduttanza d’uscita g0
g0 = β (VGS − VT ) − VDS
g0 = 0
g0 = IDS0 λ
(in zona triodo)
(in zona di saturazione con λ = 0)
(in zona di saturazione con λ , 0)
(7)
ed una transconduttanza di bulk αgm
1
α=γ √
2 VSB + 2ΦF
(8)
La corrente alle variazioni è dunque
iDS = gm vGS + g0 vDS + αgm vSB
(9)
Funzionamento ad alta frequenza del transistore MOS
Il funzionamento del transistore MOS a frequenza non nulla può essere valutato
mediante il modello a controllo di carica. In qualsiasi componente controllato
da una tensione V, se la tensione cambia da V1 a V2 , anche la carica contenuta
al suo interno deve per forza cambiare, e quindi deve scorrere della corrente.
Poiché la carica interna sarà funzione della polarizzazione (ovvero una Q(V)), è
sempre possibile definire una capacità differenziale
C=
dQ
dV
da cui la corrente che manca è una
i=
dQ
dV
=C
dt
dt
Le capacità differenziali di questo tipo costituiscono il principale effetto
capacitivo del MOS. Si tratta di capacità non lineari che cambiano molto a
seconda della polarizzazione del transistor. Esse derivano da effetti fisici diversi:
• CGD e CGS sono capacità differenziali che descrivono la variazione della
carica mobile del canale e sono quasi nulle a transistore spento. Dipendono
sia da VGS che da VGD . Se VDS = 0, il canale è orizzontale e
Qm = Cox (VGS − VT )
9
Figura 4: Capacità parassite del transistore MOS
Se si aumenta VGS , altra carica viene portata nel canale attraverso una
corrente che, poiché VDS = 0, sarà simmetrica. Dunque in questo caso
CGS = CGD . Se VDS , 0, invece, la corrente passa sempre più attraverso il
source e sempre meno attraverso al drain, fino ad arrivare a saturazione,
dunque CGS > CGD . Parallela a questa capacità, vi è una capacità costante
dovuta alla piccola zona di sovrapposizione fra il drogaggio n+ dei terminali
source e drain e il metallo del terminale di gate.
• CSB e CDB vengono dalla giunzione n+ p− , che è un diodo in inversa.
Anch’esse sono uguali per VDS = 0 e si differenziano per VDS > 0.
• CGB modella una complessa variazione di carica fra gate e bulk ed è trascurabile sopra soglia ma è la capacità caratteristica del transistore quando
esso è spento. Come già osservato prima, in senso trasversale il transistore
MOS è un condensatore: esiste una tensione, detta tensione di flatband
VFB (circa −1V), per cui esso è scarico (infatti, per via della giunzione,
non applicando nessuna tensione ci sarebbe un movimento di carica: il
condensatore si comporterebbe come una pila). Se la tensione fra gate e
bulk si riduce a 0, il gate tende a caricarsi positivamente sulla superficie a
contatto con l’ossido, mentre nel bulk, che non è un buon conduttore, la
carica negativa non si concentra tutta sulla superficie dell’ossido ma occupa
un’area più ampia. Infatti, gli elettroni, muovendosi verso l’interfaccia con
l’ossido dove si accumulano formando la carica mobile, lasciano scoperti
atomi di boro di drogaggio intrappolati nel cristallo che formano una carica
fissa (e nota), la maggior parte. Aumentando la VGS , il canale si riempie
sempre di più di carica mobile, finché questa non supera la carica fissa, e il
transistor si accende (VGS = VT ). Se si sposta una carica ∆Q da un punto
10
all’altro del silicio situato a distanza d, la variazione di campo elettrico sarà
∆E = ∆Q
dunque
ε
ε
∆Q
=
∆V
d
è un buon modello per la capacità differenziale. Essa diminuirà all’aumento
della tensione (poiché aumenta la distanza), ma quando la carica mobile
diventa rilevante torna ad aumentare.
Nella pratica, almeno per il calcolo a mano, si lavora spesso con valori fissi, con
il metodo del caso peggiore.
11
LOGICA FCMOS
Invertitore CMOS statico
In logica FCMOS (fully complementary MOS) si utilizzano insieme transistor
NMOS e PMOS per garantire alle porte logiche alcune utili proprietà. Innanzitutto,
un invertitore CMOS (il circuito FCMOS per eccellenza) è statico, ovvero mantiene
il proprio stato finché è mantenuto collegato all’alimentazione. Ha poi delle
buone proprietà come un’adeguata non-linearità, un ottimo swing logico (da 0 a
VDD ) ed è simmetrico.
Figura 5: Invertitore CMOS
Il funzionamento dell’invertitore è il seguente:
• per Vin = 0V, VGSn = 0V e dunque il transistore n è spento. VGSp =
−VDD quindi il transistore p è acceso. Fra VDD e massa non c’è corrente,
dunque l’uscita è necessariamente VDD . Tale situazone si mantiene anche
aumentando la Vin , fino a quando non si raggiunge la tensione necessaria
affinché VGS superi la tensione di soglia. Tale tensione è detta tensione di
overdrive:
Vov = VGS − VT
(10)
• per Vin = VDD , VGSn = VDD e VGSp = 0: la situazione è del tutto simmetrica alla precedente: anche qui la corrente è nulla e, poiché l’unico transistore
12
acceso è quello n, la tensione d’uscita è necessariamente 0 fino a quando
non si diminuisce Vi n fino a VDD − VT n
• nella zona intermedia, tutti i transistori sono accesi. Se
Vin − VT n > Vout
il transistore n è in zona triodo, mentre se
Vin − VT n < Vout
esso lavora in zona di saturazione; viceversa per il transistore p.
Figura 6: Caratteristica statica dell’invertitore CMOS
Quando entrambi i transistori sono in saturazione, dalle espressioni della
corrente si ricava che Vin non è più una funzione, bensì un numero:
βn
βp
(Vin − VT n )2 =
(Vin − VDD − VT p )2 ⇒
2
2
s
βn
⇒
(Vin − VT n ) = VT p − (Vin − VDD )
βp
13
Quindi qui la caratteristica è verticale e Vin è la soglia logica VLT . Nelle
altre due zone, la caratteristica statica si raccorda con le due zone a corrente
nulla.
La soglia logica o logic threshold VLT dell’invertitore si può trovare semplicemente risolvendo la precedente equazione:
r 0 W
βn ( )
VDD + VT p + VT n β 0 WL n
n ( L )p
r 0 W
VLT =
(11)
βn ( L )
n
1+
0
βn ( W
L )p
La scelta di una VLT simmetrica è generalmente la migliore. In tal caso,
VLT =
VDD
2
La condizione affinché l’invertitore sia simmetrico è che i due transistori abbiano
le stesse proprietà:
W
W
0
0
βn
= βp
L n
L p
Poiché la differenza fra la conducibilità intrinseca del transistore p e di quello n
sta nella differenza fra le mobilità di elettroni e lacune, si ricava facilmente che
µn W
W
=
(12)
L p µp L n
dove generalmente
µn
µp
≈ 2, 5 ↔ 3.
Volendo, spendendo un altro grado di libertà, si può progettare un gate ad
area minima e simmetrico ponendo
r
L
W
µn
=
=
(13)
L p
W n
µp
In realtà, l’invertitore ad area minima non è in generale il più conveniente:
infatti ci si priva di un grado di libertà che invece si rivela utile per controllare il
tempo di propagazione dell’invertitore.
Il transitorio dell’invertitore è legato al suo carico: un oggetto piuttosto
complesso poiché a carico di un gate ci saranno diversi altri gate oltre alle linee di
interconnessione. In prima approssimazione, considereremo le interconnessioni
14
dei semplici corticircuiti caratterizzati da R = 0, L = 0, C = 0: i gate a carico,
poichè il principale effetto parassita del transistore MOS sono le sue varie capacità,
costituiscono un carico di tipo capacitivo. La seconda approssimazione è che,
essendo tali capacità non lineari, le si assumeranno uguali ad una costante
(peggiorativa) Cin che definiremo come capacità d’ingresso di un invertitore
(per gate di tipo diverso, assumeremo la stessa Cin . Con tali approssimazioni,
consideriamo il transitorio in discesa. All’inizio VDD − VT n 6 V0 , dunque il
transistore è in saturazione:
dV0
IC = −CL
dt
dV0
= dt
−CL βn
(VDD − VT n
2
Integrando fra VDD e VDD − VT n (zona di saturazione), si ottiene che
τFsat =
CL VT n
βn
(VDD − VT n )2
2
Per la zona triodo si considera
−CL
βn
dV0
= dt
(VDD − VT n )V0 − 21 V02
e si integra fra VDD − VT n e VOLmax :
τFlin
1
2CL
=
βn 2(VDD − VT n )
2(VDD − VT n ) − VOLmax
log
VOLmax
Sommando le due componenti, si ottiene il tempo di discesa. Poiché, nel dimensionamento simmetrico, questo tempo coincide necessariamente con il tempo di
salita, la media fra i due, cioè il tempo di propagazione, è
1
VT n
2(VDD − VT n ) − VOLmax
2CL
1
τPD = W 0
+ log
V
−
V
V
−
V
2
VOLmax
β
DD
T
n
DD
T
n
n
L n
(14)
Gli effetti delle interconnessioni, in effetti, si possono riassumere approssimativamente sostituendo le interconnessioni con celle RC. In tal caso le formule di
Elmore permettono di stabilire un limite superiore per il ritardo delle celle:
T 1 = R1 C 1
T2 = (R1 + R2 )C2
T3 = (R1 + R2 + R3 )C3
...
15
(15)
Inoltre, ad alte frequenze, gli effetti di tipo propagatorio non sono più
secondari: dunque le linee di interconnessione devono essere modellate come
celle RLC. Un altro fenomeni che complica ulteriormente la modellizzazione è il
crosstalk: linee di interconnessione vicine possono accoppiarsi capacitivamente
e quindi scambiarsi parte del segnale.
Nel modello più semplice, le varie capacità parassite possono essere portate
tutte all’ingresso del gate: le capacità che operano fra ingresso e uscita vengono
moltiplicato per 1 − AV (effetto Miller). In questo modo, un modello ragionevole
per la capacità d’ingresso dell’invertitore è
!
W
W
+
Cin = Ki Cox L2
= Ki Cox (WL)n + (WL)p ≈ 10−14 F (16)
L n
L p
dove Ki è un coefficiente sull’ordine di 1-10 (se non segnalato, lo si suppone
uguale a 1). La Cout avrà anch’essa una forma simile. Questo modello è ampiamente semplificato, ma permette di capire il funzionamento di un circuito
senza complicazioni matematiche eccessive; per risultati più esatti è necessario
simularlo.
Un metodo ancora più semplificato per calcolare i tempi di propagazione è
considerare il transistor come una resistenza equivalente controllata da un transistore: tale resistenza è calcolata come una media della funzione dVdDS IDS (VDS )
ed è detta resistenza equivalente. In questo modo il resistore può essere trattato
esattamente come un comune circuito RC. Il tempo di salita o di discesa fra il
10% e il 90% è dunque
t10%−90% = Req CL log 10
(17)
mentre quello necessario per raggiungere la soglia logica è
t50% = Req CL log 2
(18)
Per il dimensionamento dei transistor, spesso conviene definire una resistenza
equivalente di riferimento, cioè quella per VGS = VDD per il transitorio 10% −
90% e con W
= 1. In tal caso, si può dimensionare un transistor utilizzando
L
questa formula:
W
Reqrif W
=
(19)
L n
Reqn
L rif
Ovviamente, lo stesso vale per transistori p.
16
Buffer e tri-state
Generalmente i gate CMOS devono tenere a carico capacità dell’ordine di
10−14 F. Se le capacità sono più grandi, come spesso accade quando si esce
dal chip, il modo più efficiente per gestirle mantenendo minimo il tempo di
propagazione è utilizzare una serie di N invertitori sempre più grandi di un fattore
G. Minimizzare il tempo di propagazione significa minimizzare τtot , essendo
τtip e Ctip rispettivamente il tempo di propagazione e la capacità d’ingresso
dell’invertitore a dimensionamento tipico:
τtot = (N + 1)τtip G
Ctip GN+1 = CL
da cui
Ponendo
si ottiene
G
CL
τtot =
log
log G
Ctip τtip
CL
1
N+1 =
log
log G
Ctip
dτtot
=0
dG
G=e
(20)
N = log
CL
Ctipica
−1
Questo è anche il buffer ad area minima. In ogni caso, volendo utilizzare un
diverso numero N di invertitori nel buffer, la soluzione migliore è porre
s
CL
(21)
G = N+1
Ctipica
Un altro problema che può essere risolto con l’utilizzo dei buffer, oltre a
grandi capacità a carico, è quello dei circuiti che condividono un’uscita. È chiaro
se le uscite di due circuiti in parallelo sono ad esempio uno 0 ed 1, si forma
sull’uscita comune un nodo di conduzione fra alimentazione e massa che non
dovrebbe esistere e che assumerà un potenziale intermedio fra 0 e VDD . Per fare
in modo che solo un circuito alla volta utilizzi una certa linea come uscita, e
dunque evitare questo problema, si utilizzano i buffer tristate: buffer controllati
da un segnale di enable che, se disattivato, porta l’uscita del buffer in uno stato
17
detto di alta impedenza. In tale stato tutti i transistor dello stadio finale del buffer
sono spenti e dunque il nodo d’uscita è ad alta impedenza. Un simile buffer
può essere realizzato facilmente anteponendo qualche stadio di circuiti logico
agli invertitori del buffer. Dal punto di vista del dimensionamento, tali porte
logiche (FCMOS) possono essere facilmente ricondotte ad invertitori e dunque
non costituiscono un problema ulteriore.
Gate FCMOS
L’invertitore CMOS costituisce la base su cui vengono costruiti tutti i gate FCMOS.
Tutti i gate sono costituiti da una rete di pull up di transistori PMOS e da una di
pull down di transistori NMOS, dimensionate generalmente in modo simmetrico.
La funzione logica della rete è già contenuta tutta in una delle due reti.
Figura 7: Gate FCMOS generico
La rete di pull up è posta fra uscita e alimentazione e ha il compito di
tenere alta la tensione d’uscita; la rete di pull down è posta fra uscita e massa
18
ed ha il compito esattamente opposto. La procedura per implementare una
funzione logica generica consiste solitamente nel ricondursi ad una forma del
tipo f = (. . . ). In una forma del genere, nella rete di pull down gli OR sono
costituiti da transistori in parallelo e gli AND da transistori in serie. Costruita
la rete di pull down, si può costruire in modo simmetrico la rete di pull down,
convertendo le serie in paralleli e i paralleli in serie.
Alcune difficoltà nel progetto di gate FCMOS più complessi dell’invertitore
sono:
• transistori con VSB non sempre nullo, quindi presenza dell’effetto Body;
• nodi di segnale non collegati a massa o alimentazione, quindi presenza di
capacità equivalenti verso massa;
• glitch dell’uscita, ovvero commutazioni non desiderate dovute al tempo di
propagazione non nullo;
• transistori in serie.
In particolare, il fatto di avere transistori in serie limita la corrente e dunque
rallenta i dispositivi. In prima approssimazione, non considerando l’effetto body,
due transistori si comportano come un unico MOS di lunghezza doppia, ovvero,
poiché I ∝ W
, un unico MOS che conduce la metà. Per non peggiorare il tempo
L
di propagazione, dunque, è necessario dimensionare con un fattore di forma
doppio rispetto al normale. In generale, per non sommare questo effetto a quello
della minore mobilità nei transistori p, si cerca di tenere le serie di transistori il
più possibile nella rete di pull down: ad esempio, il gate NAND è più piccolo del
cugino NOR (se µµnp = 3, il NOR occupa 14 unità di area e il NAND 10).
In generale, il fattore di forma equivalente di una serie di n transistor è
W
1 W
=
(22)
L eq n L
Per non diminuire la velocità del gate, è dunque necessario sovradimensionare
i transistor di un fattore n.
19
LOGICHE NON FCMOS
Pass transistor e transfer gate
Non tutte le funzioni logiche sono convenientemente implementate utilizzando
solo logica FCMOS. Il modo più semplice per utilizzare i transistor è sfruttarli
semplicemente come interruttori che permettono al segnale di passare oppure
no: i pass transistor. Il suo funzionamento di base è ovvio: quando si ha una
Figura 8: Pass transistor
tensione alta sul gate, il segnale passa, altrimenti non passa. Molto più complessi
e interessanti sono i suoi problemi:
• portare a 1 l’uscita significa fondamentalmente caricare una capacità CL ,
operazione che gli NMOS svolgono in modo non molto efficiente. Infatti l’aumento della tensione di uscita (con VDD in ingresso) diminuisce
l’overdrive:
Vov = VDS − VT n = VDD − VCL − VT n
Quando la tensione di uscita raggiunge VDD − VT n , il transistore si spegne,
e l’uscita non raggiunge mai la tensione di alimentazione;
• il problema al punto precedente è peggiorato dal fatto che VSB aumenta e
dunque VT n > VT 0 per l’effetto body;
• lo spegnimento del pass transistor (transizione 1 → 0 sul gate) porta alla
formazione di un partitore capacitivo fra la capacità CL a carico e la capacità
d’uscita del gate stesso: la tensione di uscita dunque si abbassa rispetto a
quella a pass transistor acceso; tale fenomeno è denominato ripartizione
di carica;
• anche in condizioni statiche, con il pass transistor spento, il nodo d’uscita è
ad alta impedenza e dunque la carica in esso contenuta tende a “sfuggire”
anche per effetti piccolissimi come la corrente in inversa dei diodi contenuti
nel transistor;
20
• il potenziale del condensatore è abbassato anche dalla carica contenuta
nel canale che, quando il transistore viene spento, defluisce verso drain e
source.
I numerosi problemi del pass transistor (comunque non sufficienti a renderlo
un oggetto inutile) sono in buona parte risolti nel transfer gate, che unisce un
transistor NMOS con un PMOS che ha caratteristiche simili ma complementari
(non è necessario che sia dimensionato in modo simmetrico). Il transfer gate
Figura 9: Transfer gate
compensa buona parte dei problemi del transfer gate e permette di portare a
VDD l’uscita.
Multiplexer a pass transistor
Figura 10: Multiplexer a 2 ingressi
21
Un utilizzo particolarmente interessante del pass transistor è il multiplexer,
circuito che permette di realizzare funzioni differenziate a seconda degli ingressi
Vi .
Con un MUX si può realizzare in teoria qualsiasi funzione logica; in pratica
questo avviene a scapito della velocità, in particolare per la presenza di serie
di molti transistor e per i difetti analizzati precedentemente. Ciononostante, la
semplicità di questo circuito lo rende comunque attraente dal punto di vista
progettuale.
Circuiti domino
Poiché in un circuito FCMOS la rete di pull down determina già l’intera funzione
logica, è possibile costruire un circuito che comprenda solo questa parte. Tale
circuito, però, sarà dinamico e non statico come un circuito FCMOS. Tale tipologia
di circuiti è detta domino o ripple.
Figura 11: Gate domino generico
Il funzionamento del gate domino si suddivide in una fase di precarica in cui
l’uscita OUT è incondizionatamente alta: CL = 0 e la “rete di pull up” costituita
unicamente da un transistore p mantiene alta l’uscita. Quando CL = 1, si passa
alla fase di valutazione, in cui la rete di pull down, attivata dal transistore n,
22
scarica il nodo OUT se necessario, a seconda degli ingressi e della funzione logica
implementata.
Di fatto, nella fase di precarica si assiste alla carica di un condensatore che
nella fase di valutazione può essere scaricato, se si forma un percorso conduttivo
verso massa, o mantenuto nel suo stato, nel caso che tale percorso non si ferma.
In quest’ultimo caso, il nodo OUT è collegato al resto del circuito mediante
transistori spenti: è un nodo ad alta impedenza che tenderà a scaricarsi in qualche
modo se CL non è abbastanza rapido. Questo rende i circuiti domino di tipo
dinamico. Tuttavia, non si tratta di circuiti sincroni poiché il segnale si propaga
come in un blocco combinatorio. L’invertitore alla fine del circuito serve sia ad
alzare la capacità per ridurre gli effetti di ripartizione di carica, sia per fare in
modo che i transistori del successivo gate rimangano spenti in fase di precarica.
La logica domino permette di ridurre l’area occupata da gate con molti
transistor (quasi alla metà che nel caso FCMOS) ma in cambio richiede un clock
e non è statica.
Ripartizione di carica nei circuiti dinamici
La ripartizione di carica o charge sharing è un fenomeno tipico dei circuiti
dinamici, in cui l’informazione viene immagazzinata temporanemante in nodi
ad alta impedenza sotto forma di carica elettrica.
Figura 12: Ripartizione di carica
Utilizzando un normale interruttore, che viene chiuso fra due capacità C1 e
C2 , s ha che
C1 V1 + C2 V2
Vf =
C1 + C2
Utilizzando un transistor, sono in gioco anche due capacità parassite CA e CB . Se
23
∆Φ è la variazione del clock che controlla il gate del pass transistor,
Vf =
V1 (C1 + CA ) + V2 (C2 + CB ) + ∆Φ(CA + CB )
C1 + C2 + CA + CB
(23)
La ripartizione di carica crea molti problemi per i circuiti dinamici, poiché
quando si formano nodi ad alta impedenza (ad esempio nei circuiti domino se
OUT non deve essere scaricato in fase di valutazione) si formano ovviamente
paralleli di capacità parassite. Tenere alte le tensioni dei nodi per un tempo
sufficiente è uno dei problemi principali di progetto nei circuiti dinamici.
Circuiti sincroni
Nei circuiti sincroni l’elaborazione avviene in due stadi, ripetuti in maniera successiva: una rete combinatoria che elabora i segnali binari in ingresso attraverso
opportune funzioni logiche, separati attraverso un interruttore (temporizzato
da un segnale di clock da blocchi di memoria che mantengono i valori ricevuti
al precedente intervallo di clock e alimentano altre reti combinatorie: e il ciclo
ricomincia. In questo modo l’elaborazione si “propaga” e in ogni periodo di clock
una rete combinatoria elabora il risultato che la precedente rete combinatoria ha
elaborato nel precedente periodo di clock.
Figura 13: Esempio di circuito sincrono con due clock sfasati
Il modo più inefficiente ma anche più semplice per far propagare l’elaborazione è mediante due clock sfasati Φ1 e Φ2 . È un metodo inefficiente, in quanto
bisogna conoscere e mantenere costanti lungo tutto il chip ben due parametri:
il periodo di clock (che deve essere paragonabile al tempo di propagazione
τPD ) e soprattutto lo sfasamento, che è molto difficile da tenere costante. Nei
chip moderni si usano dunque soluzioni differenti, ad esempio pass transistor
alternativamente n e p controllati da un unico clock.
Nei circuiti sincroni, il blocco di memoria può essere fondamentalmente di
due tipi: memoria statica, che sfrutta la retroazione positiva di due invertitori
per mantenere immagazzinato un dato, e memoria dinamica, che immagazzina l’informazione in una capacità (ad esempio nella capacità parassita di un
transistore MOS), ma solo per un breve periodo di tempo.
24
MULTIVIBRATORI
Multivibratori bistabili
I multivibratori sono circuiti che sfruttano la retroazione positiva di invertitori
per ottenere effetti particolari, quali memorizzare un dato, riportare un’uscita a
un certo livello dopo qualche tempo o produrre una oscillazione.
Figura 14: Bistabile fondamentale
Il multivabratore più semplice, detto bistabile, è costituito da due invertitori
chiusi in retroazione l’uno sull’altro. Un circuito di questo tipo ha tre punti di
equilibrio: due in cui gli invertitori lavorano in “regime digitale” (con 1 e 0) e a
guadagno praticamente nullo, e uno in cui tutte le tensioni corrispondono alla
soglia logica VLT , e il guadagno è molto elevato. Mentre i primi due punti sono
stabili, in quello ad alto guadagno basta una piccola perturbazione ed il circuito
si porta autonomamente in una delle due situazioni stabili (questa è la ragione
del suo nome).
Aggiungendo qualche circuito per controllare il dato, il bistabile può essere
reso adatto a memorizzare informazione in modo statico: questo tipo di circuiti
sono denominati flip-flop.
Figura 15: Flip-flop set-reset a livello logico
Il più semplice flip-flop set-reset (reso sincrono mediante l’aggiunta dei
due AND) ha una configurazione vietata: la 11 se è realizzato a NOR, la 00 a
NAND. Passando a tale configurazione, infatti, il circuito diventa instabile e
25
quindi l’uscita assume un valore casuale, o 0 o 1. Il clock impedisce all’uscita di
modificarsi fintantoché rimane a 0. Finché CK = 1, questo circuito però risente
di ogni cambiamento sugli ingressi (anche uno non voluto): si dice che esso è
sensibile ai livelli.
In effetti non è necessario usare tutti quei gate per implementare un flip-flop
SR: sono sufficienti 8 transistor. Il funzionamento del circuito ha comunque come
cuore una coppia di invertitori.
Figura 16: Flip-flop set-reset a livello circuitale
Per eliminare la sensibilità ai livelli, si può rendere sensibile il circuito solo
alle variazioni in un tempo pari al ritardo di propagazione di un invertitore,
come avviene nel flip-flop SR che segue.
Rimane ancora il problema degli ingressi vietati. Per eliminarlo, esistono
svariate altre tipologie di flip-flop, quali il JK e il D, realizzabili anteponendo a
un flip-flop SR altri circuiti logici. Inoltre, per utilizzare i flip-flop come linee
di ritardo, esiste una particolare configurazione di due flip flop in cascata,
detta master-slave. Tutte queste configurazioni sono molto utilizzate nei circuiti
dinamici
26
Figura 17: Flip-flop set-reset non sensibile ai livelli
Multivibratori monostabili
Il multivibratore monostabile è un circuito che tende ad assumere un unico valore
stabile, anche se viene commutato. La retroazione positiva rende piccolissimo il
tempo di propagazione, che tende ad essere nullo rispetto alla costante di tempo
RC del circuito.
Figura 18: Multivibratore monostabile
All’equilibrio, il condensatore C è un circuito aperto e così anche l’invertitore,
che ha necessariamente ingresso alto e uscita bassa. Dunque il nodo A si trova a
potenziale alto. Questo implica che in equilibrio C sia scarico. Il guadagno d’anello
è nullo e il circuito è stabile. Mandando Vin a 1, il nodo A passa istantaneamente
(per quanto detto prima sul tempo di propagazione) a 0 e, poiché in un tempo
nullo la tensione sul condensatore non può cambiare, trascina a 0 anche il nodo
B: questo effetto è denominato bootstrap. Trovandosi a potenziale basso ma
collegato a VDD attraverso una resistenza, il condensatore tenderà a ricaricarsi
portando in alto VB come un circuito di costante RC. Finché VB rimane sotto la
soglia logica VLT , l’uscita del circuito rimane alta (indipendentemente da Vin
27
che nel frattempo può tornare basso). Non appena VB supera VLT , l’invertitore
scatta portando a 0 l’uscita e facendo scattare la tensione VB a VDD + VLT (questo
fra l’altro è l’unico modo per portare in un circuito digitale una tensione più
alta dell’alimentazione). Dopo un tempo di scarica, anch’esso con costante RC,
il circuito si ritrova nella situazione iniziale. La durata dell’impulso prodotto,
sulla base di questo ragionamento, è data da
t
VB (t) = VB (∞) + VBin − VB (∞) e− RC
t
VLT = VDD (1 − e− RC )
per cui
∆t = RC log
VDD
VDD − VLT
(24)
Dopo la fine dell’impulso, prima di poterne produrre uno nuovo, bisogna
aspettare che il condensatore si scarichi. Considerandolo scarico a VB = 1, 1VDD
(in linea di principio ci vuole un tempo infinito per scaricarlo), il tempo di
recupero è data da
t
0, 1VDD = VLT e− RC
e quindi
∆tR = RC log
VLT
0, 1VDD
(25)
Multivibratori astabili
Figura 19: Multivibratore astabile
Il multivibratore astabile non ha un punto di lavoro stabile: l’unico punto di
equilibrio è la soglia logica poiché, in condizioni statiche, il primo invertitore
è retroazionato su se stesso e C è un circuito aperto. Se Vout commuta verso il
basso, significa che l’ingresso del secondo invertitore ha commutato verso l’alto,
28
ovvero che VA è sceso sotto VLT . VA cerca di risalire verso VDD , ma quando arriva
a VLT fa commutare gli invertitori e, per effetto bootstrap, è portato a VDD + VLT :
comincia quindi un transitorio di discesa, ma di nuovo quando arriva a VLT fa
commutare gli invertitori, e il ciclo ricomincia. L’astabile dunque genera un’onda
quadra digitale. Il duty cycle può essere calcolato in modo analogo alla durata
dell’impulso nel monostabile: l’intervallo di tempo in cui il segnale è basso è
τL = RC log
2VDD − VLT
VDD − VLT
(26)
mentre quello in cui il segnale è alto è
τH = RC log
VDD + VLT
VLT
(27)
Questo circuito, contrariamente alle apparenze, non può essere utilizzato per
generare il segnale di clock perché la costante RC non può essere troppo piccola
(altrimenti entrano in gioco capacità e resistenze parassite che la renderebbero
imprecisa). Per generare il clock si usano circuiti particolari con isteresi come il
trigger di Schmitt.
29
LICENZA
Questi appunti sono rilasciati sotto licenza Creative Commons BY-NC-SA.
Chiunque è libero
• di riprodurre, distribuire, comunicare al pubblico, esporre in pubblico,
rappresentare, eseguire e recitare quest’opera
• di modificare quest’opera
a patto che
• la paternità di questi appunti rimanga attribuita a me
• non vengano utilizzati per fini commerciali
• se modificati, vengano rilasciati nuovamente sotto licenza CC BY-NC-SA
Per ulteriori informazioni sulla licenza, visitate
http://creativecommons.org/licenses/by-nc-sa/3.0/deed.it
L’immagine sulla copertina, rilasciata sotto licenza Creative Commons BY, è
opera dell’utente naotakem su Flickr ed è reperibile all’indirizzo
http://www.flickr.com/photos/naotakem/148029355/
Gli appunti sono rilasciati senza alcuna garanzia sulla loro correttezza: sono
probabilmente pieni di lacune, errori (di battitura e/o di concetto) ecc. Se qualcuno
rilevasse un errore di questo genere, è pregato di segnalarlo con un commento
sul mio blog:
http://www.arunax.netsons.org
30