TECNICHE DI GESTIONE ,CONDUZIONE DI MACCHINE ED IMPIANTI
APPUNTI -CLASSI QUARTE
Gli appunti sono da integrare con gli argomenti e/o esercizi svolti nelle lezioni.
MODULO 1- RICHIAMI DI GEOMETRIA
FIGURE GEOMETRICHE SEMPLICI
Si indica con P= perimetro , A=area
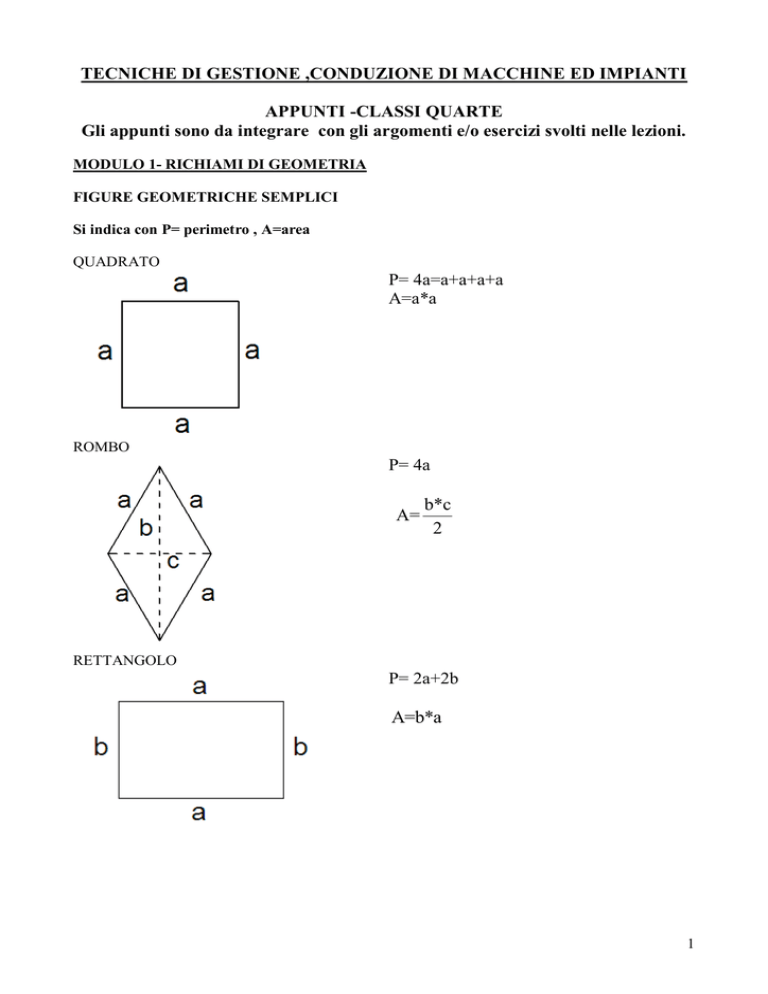
QUADRATO
P= 4a=a+a+a+a
A=a*a
ROMBO
P= 4a
A=
b*c
2
RETTANGOLO
P= 2a+2b
A=b*a
1
TRIANGOLO QUALSIASI
P= a+b+c
A=
c*h
2
La somma degli angoli interni di un
triangolo è di 180°
α+β+γ=180°
α= alfa, β=beta, γ=gamma
TRIANGOLO RETTANGOLO
HA UN ANGOLO DI 90°
P= a+b+c
l’area tratteggiata del triangolo è pari alla
metà dell’area del rettangolo di lati a,b
A=
a*b
2
Teorema di Pitagora.
si ha che c2 =a 2 +b2 ,
l’ipotenusa c è pari alla somma
dei quadrati dei due lati a, b.
quindi:
a 2 =c2 -b2 ; b2 =c2 -a 2
c= a 2 +b2
.
TRAPEZIO
P= d+a+f+c
.
A
(d a ) h
2
2
TRAPEZIO RETTANGOLO
P= d+a+h+c
.
A
(d a ) h
2
.
l’area A del trapezio può essere
calcolata come somma dell’area A1
del rettangolo di lati a,h e dell’area A2
del triangolo rettangolo di lati b , h
A=A1+A2
.
Esempio
P= 6+16+c+f
i lati c, d si ricavano con il teorema di
Pitagora.
c= 42 +72 8
f= 62 +72 9, 2
l’area A del trapezio può essere calcolata
come somma delle aree A1,A2,A3
A1=6*7= 42 cm2
A2=6*7/2=21 cm2
A3=4*7/2=14 cm2
A=A1+A2+A3=42+21+14=77 cm2
oppure
A=(16+6)*7 /2=77 cm2
3
CERCHIO DI RAGGIO R E CENTRO C
L (lunghezza della
circonferenza)=2*π*R
angolo giro =360°
π=pi greco ≈3.14
A (area)= π*R2
.
META’ CERCHIO RAGGIO R
L=2*π*R/2 (la lunghezza L è pari alla
metà della lunghezza del cerchio)
angolo piatto (uguale alla metà di
quello del cerchio) =360°/2=180°
A= π*R2/2 (l’area è uguale alla metà
dell’area del cerchio )
.
4
QUARTO DI CERCHIO RAGGIO R
L =2*π*R/4 (la lunghezza L è pari ad
un quarto della lunghezza del cerchio)
angolo (uguale ad un quarto di quello
del cerchio) =360°/4=90°
A = π*R2/4 (l’area è pari ad un quarto
dell’area del cerchio )
.
CORONA CIRCOLARE ( ANELLO)
P=2*π*R+2*π*r
(il perimetro è pari alla somma delle
lunghezze delle circonferenze di raggio
R e r)
A= π*R2- π*r2
(l’area è pari alla differenza tra l’area
del cerchio di raggio R e quella del
cerchio di raggio r)
.
CONVERSIONE DEGLI ANGOLI DA GRADI A RADIANTI
Angolo α tra due segmenti AO e BO.
Gli angoli possono essere espressi in gradi ( esempio 45°) oppure in radianti (esempio π/4)
Esiste una corrispondenza biunivoca tra l’angolo espresso in gradi ed il suo corrispondente espresso
in radianti.
Per convertire un angolo da gradi a radianti si usa la formula:
5
αrad =
π
α°
180
( angolo alfa in radianti)
esempio con α°=45°:
π
3.14
αrad =
45°=
45°=0.785 radianti
180
180
l’angolo giro α=360° corrisponde a α=2π radianti
l’angolo retto α=90° corrisponde a α=π/4 radianti
l’angolo piano α=180° corrisponde a α=π radianti
l’angolo α=270° corrisponde a α=3π/2 radianti
y
x
SETTORE CIRCOLARE DI RAGGIO R E ANGOLO α QUALSIASI
rad
L= R*α
(la lunghezza L
dell’arco è pari al raggio R
moltiplicato per l’angolo αrad del
settore espresso in radianti)
π R2
A=
α°
360
L’area A del settore circolare si trova
impostando la proporzione:
Angolo α°: 360° = Area del settore :
Area del cerchio
6
CALCOLO DI AREE DI FIGURE GEOMETRICHE COMPLESSE.
Il calcolo delle aree di figure geometriche piane può essere determinato tramite la somma o la
sottrazione delle aree delle figure geometriche semplici trattate, per geometrie più complesse è
conveniente l’utilizzo del software CAD 2D.
CALCOLO DELLA PERCENTUALE DI SFRIDO.
DEFINIZIONI
At= area totale del materiale dal lavorare ( tessuto, cuoio, etc)
Am= area totale del modello/sagoma che si intende realizzare
Asf= area di sfrido ( area del materiale di scarto a seguito del taglio)
%Sf= percentuale di sfrido
PIAZZAMENTO= posizionamento delle sagome sul tessuto da tagliare per ottenere la minore
percentuale di sfrido.
QUOTATURA DEL MODELLO= assegnazione di tutte le lunghezze (quote) per poterlo
riprodurre fedelmente .
Le sagome da realizzare vengono posizionate sul tessuto in lavorazione in modo da ottenere la
minor percentuale di sfrido (quindi minore scarto di materiale)
FORMULE DI CALCOLO
Asf=At - n*Am
n= numero di modelli uguali
%Sf=
Asf*100%
At
( si utilizza la proporzione %Sf: Asf=100% : At)
Se le sagome da realizzare hanno forme diverse l’area totale Am del modello sarà data dalla
somma delle aree di tutti i modelli
Am= A+B+F+E+P ( esempio figura seguente)
7
L’utilizzo di appositi software CAD permette il calcolo automatico del piazzamento delle sagome
in modo da ottenere la minor percentuale di sfrido .
8
ESERCIZI
esercizio 1
dimensioni in cm
Calcolare la percentuale di sfrido
At=40*18=720 cm2 (area totale tessuto)
9
Am=π*R2=3.14*52=78.5 cm2 (area totale modello)
Asf=At-n*Am=720- 4*78.5=406 cm2 (area sfrido)
%Sf=
Asf*100% 406*100%
56.3% (percentuale di sfrido)
At
720
lo scarto ( 56.3%) è pari a circa la metà del tessuto di partenza (100%)
esercizio 2
Calcolare la percentuale di sfrido e l’area del modello.
dimensioni in cm
Soluzione
At=22*36=792 cm2 (area totale tessuto)
in questo caso è più semplice calcolare prima l’area dello sfrido che è la somma delle aree A1, A2,
A3
Asf= A2+A1+A3
A1=A3=22*10/2 =110 cm2 (area del triangolo rettangolo)
A2= π*R2 /2=3.14*82/2≈100.5 cm2 ( area di metà cerchio di raggio R=8)
Asf= A2+A1+A3= 110+110+ 100.5 =320.5 cm2 (area sfrido)
10
dalla formula Asf=At-n*Am
n*Am=At-Asf
si ricava
( con n=1)
1* Am= 792-320.5=471.5 cm2 (area del modello)
%Sf=
Asf*100% 320.5*100%
40.5% (percentuale di sfrido)
At
792
esercizio 3
dimensioni in cm
11
Soluzione
At=34*40=1360 cm2 (area totale tessuto)
anche in questo caso è più semplice calcolare prima l’area dello sfrido come somma delle aree A1,
A2, A3
Asf= A2+A1+A3
A1=A3= π*R2 /4≈ 113 cm2 (area di un quarto di cerchio di raggio R= 12)
A2= 10*20=200 cm2 ( area del rettangolo)
Asf= A2+A1+A3= 113+113+ 200 =426cm2 (area sfrido)
dalla formula Asf=At-n*Am
n*Am=At-Asf
si ricava
( con n=1)
1* Am=1360-426=934 cm2 (area del modello)
%Sf=
Asf 100% 426 100%
31% (percentuale di sfrido)
At
1360
esercizio 4
Calcolare la percentuale di sfrido del modello seguente per n=3 sagome
dimensioni in cm
12
soluzione
Am=A1+A2+A3= 15*40+20*15/2 +30*20/2=600+150+300=1050 cm2
,
At=90*60= 5400 cm2
Asf=At-3*Am=5400-3*1050= 2250 cm2
%Sf= Asf*100% /At = 2250*100% / 5400= 41,6%
13
esercizio 5
Calcolare la percentuale di sfrido del modello seguente per n=1 sagome
dimensioni in cm
soluzione
Am=A1+A2+A3+A4+A5=3.14*122 /2+31*24+21*10+22*12/2+22*12/2
=226+744+210+132+132=1444 cm2
,
At=65*45=2925 cm2
14
Asf=At-1*Am=2925-1*1444= 1481 cm2
%Sf= Asf*100% /At = 1481*100% / 2925= 50,6%
esercizio 6
Calcolare l’area Am ( per la risoluzione si utilizza il settore circolare ed il triangolo rettangolo)
dimensioni in cm
soluzione
Am=A1-A2=3.14*202 /4 - 20*20/2=314- 200= 114 cm2
15
esercizio 7
Calcolare la percentuale di sfrido del modello seguente per n=1 sagome
dimensioni in cm
16
soluzione
At=3.14*452=6358,5 cm2
Am=A1+4*A2+4*A3+4*A4= 20*20+4*(10*30)+4*(10*20/2)+4*(3.14*102 /2) =
= 400+4*(300)+4*(100)+4*(157) ≈2628 cm2
Asf=At-1*Am=6358,5 -1*2628= 3730,5 cm2
%Sf= Asf*100% /At = 3730,5*100% / 6358,5 ≈ 58,7 %
CONVERSIONI DI LUNGHEZZE
m
1
dm
10
cm
100
mm
1000
procedendo da sinistra verso destra si moltiplica per 10 ad ogni salto di colonna
mentre da destra verso sinistra si divide per 10 ad ogni salto di colonna
esempio
m
23,5
dm
235
cm
2350
mm
23500
cm2
10000
mm2
1000000
CONVERSIONI DI AREE
m2
1
dm2
100
procedendo da sinistra verso destra si moltiplica per 100 ( si aggiungono 2 zeri) ad ogni salto di
colonna
17
mentre da destra verso sinistra si divide per 100 ( si tolgono 2 zeri) ad ogni salto di colonna
esempio
m2
23,5
dm2
2.350
cm2
235.000
mm2
23.500.000
Potenze in base 10.
10^2=100 , 10^3=1000, 10^4=10.000, 10^5=100.000 , 10^6=1.000.000
se l’esponente è negativo:
10^-2=1/100 =0,01 , 10^-3=1/1000=0,001 , 10^-4=1/10.000=0,0001, 10^-5=1/100.000 =0,00001 ,
10^-6=1/1.000.000 =0,000001
Esercizi
Convertire
245.000 mm2 in cm2
6,5 m2 in cm2
320 dm2 in m2
4230 cm2 in m2
FUNZIONE SENO E COSENO
18
In un piano cartesiano x,y di centro o dato un segmento OA di raggio R=1 che ruota in senso
antiorario di un angolo α misurato a partire dall’asse x , si definisce:
la funzione Y=sen α come lunghezza del segmento AM corrispondente all’angolo α
( i valori del seno dell’angolo α si trovano sull’asse y e sono compresi tra -1 ed 1)
la funzione X=cos α come lunghezza del segmento OM corrispondente all’angolo α
( i valori del seno dell’angolo α si trovano sull’asse x e sono compresi tra -1 ed 1 )
per α=0°
Y=sen0°=0 , X=cos0°=1
per α=90°
Y=sen90°=1 , X=cos90°=0
per α=180°
Y=sen180°=0 , X=cos180°=-1
per α=270°
Y=sen270°=-1 , X=cos270°=0
esempio se α=30°
Y=sen30°=0,5 , X=cos30°=0,866
Esercizio
Calcolare il seno e il coseno di :
α=135° , α=250° ,α=60°
APPLICAZIONE AL TRIANGOLO RETTANGOLO
Il triangolo di vertici OAM è un triangolo rettangolo, se R ha un valore diverso da 1 ( ad esempio
R=C)
si ha che:
il cateto verticale AM è a=c*sen α
il cateto orizzontale OM è b=c*cos α
19
Si definisce tangente dell’angolo α ( tg α) il rapporto tra il seno ed il coseno dell’angolo α che è
equivalente al rapporto tra i cateti a,b.
tg =
sen a
cos b
esempio: tg30°=0,577
se si conoscono i due cateti a, b del triangolo rettangolo e si vuole determinare l’angolo α
bisogna considerare ( sulla calcolatrice) la funzione inversa ( arcotg) della tangente.
a
arcotg
b
esempio: a=45 cm b=57 cm si trova
mentre per Pitagora c
α= arctg(45/57)≈ 38°
a 2 b2 452 572 72.6cm
20
esempio: determinare i cateti a,b data l’ipotenusa C=50 cm
soluzione :
a=50*sen35°= 28,6 cm
b=50*cos35°=40,9 cm
TEOREMA DEI SENI
Dato un triangolo qualsiasi
vale la regola che i lati sono proporzionali al seno degli angoli opposti.
a
c
b
sen sen sen
teorema dei seni
da cui si trovano :
b sen
c sen
,a
sen
sen
b sen
a sen
c
,c
sen
sen
c sen
a sen
b
,b
sen
sen
a
21
esempio si conoscono il lato b=29,71 cm e gli angoli α=51,7°, β=28,3°
si ha α+ β+γ=180°
da cui si ricava
l’angolo γ
γ=180°- α- β = 180°-51,7°-28,3°
=100°
dal teorema dei seni si trovano i lati a,c del triangolo:
b sen 29,71 sen51,7
49,1 cm
sen
sen 28,3°
a sen 49,1 sen100
c
61,6 cm
sen
sen51,7
a
22
esercizi.
dati i seguenti triangoli (1,2,3,4) ricavare i lati e gli angoli incogniti.
Soluzioni
Triangolo 1
β= 180- 90-31,5= 58,5° , a= 44,3*sen31,5°/sen90° ≈ 23,14
Triangolo 2
α= 180- 90-52,1≈ 37,9° , c= √(37,79^2+29,47^2) ≈ 47,9
, b=44,3*cos31,5°≈ 37,77
(teorema di Pitagora)
Triangolo 3
α=180-68-75,9≈ 36,1° , a= 46,74 *sen36,1°/sen68° ≈ 29,7 , c=46,74 *sen75,9° /sen 68°≈ 48,89
Triangolo 4
α= arctg(23,23/28,88)≈ 39,4° β= arctg(28,28/23,23) ≈ 50,59° , c=√(28,88^2+23,23^2) ≈ 36,59
23
IL PIANO CARTESIANO ORTOGONALE
Il piano cartesiano rappresenta il sistema di riferimento assoluto nel quale viene disegnato il
modello CAD ( anche il software autocad utilizza gli stessi principi trattati di seguito).
DISEGNO DI LINEE
Le linee vengono disegnate attraverso segmenti conoscendo le coordinate dei punti estremi
P1(x1,y1) e P2(x2,y2) del segmento .
i punti vengono indicati per semplicità con un numero e tra parentesi le coordinate (x,y) del punto
esempio
24
oppure conoscendo un punto estremo del segmento esempio P1(x1,y1) , la lunghezza L del
segmento ed il suo angolo α misurato in senso antiorario a partire dall’asse passante per P1
parallelo all’asse x
esempio
25
COSTRUZIONE DELLA GEOMETRIA TRAMITE PUNTI ASSEGNATI
Le figure geometriche vengono disegnate conoscendo le coordinate dei vertici in questo caso i
punti 1,2,3.,
per disegnare la geometria del modello si ricorre ad una tabella in cui vengono indicate le
coordinate x,y dei vari punti che costituiscono la geometria.
punto
1
2
3
4
5
...
x
40
-50
30
y
30
-20
-40
congiungendo successivamente i punti ottengo la figura geometrica desiderata in questo caso un
triangolo.
26
Nel caso siano presenti delle curve queste possono essere rappresentate attraverso archi di
circonferenze ( oppure curve particolari approssimate esempio spline).
Nella sagoma seguente i punti P1,P2 vengono uniti ( raccordati) attraverso un arco di cerchio di
centro C di coordinate (x,y)=(30,81) e raggio R=51.5 . Oltre alle coordinate dei punti P1,P2,P3,P4
dei segmenti occorre conoscere anche le coordinate del centro centro C della circonferenza.
DEFINIZIONE
RACCORDARE = unire 2 o più punti attraverso una linea curva
27
28
esempio : sagoma simmetrica rispetto l’asse y raccordata da un arco di cerchio di raggio r=20
costruzione tramite punti assegnati
costruzione tramite angoli e lunghezze delle linee
29












