Excel.book Page 437 Saturday, February 28, 2009 6:53 PM
Capitolo 54
Previsioni in presenza di eventi
speciali
■
Come è possibile determinare se vi sono fattori specifici che influiscono sul passaggio di clienti?
■
Come è possibile valutare la precisione di una previsione?
■
Come è possibile controllare se gli errori di previsione sono casuali?
Per un progetto degli studenti, si è cercato di prevedere il numero di clienti che visitano ogni giorno
la filiale Eastland Plaza della Credit Union presso la Indiana University (IU). Parlando con il direttore
della filiale è emerso che il numero di clienti era influenzato dai seguenti fattori:
■
Mese dell’anno
■
Giorno della settimana
■
Se nel giorno avvenivano pagamenti della facoltà o del personale
■
Se il giorno precedente o successivo era una vacanza
Come è possibile determinare se vi sono fattori specifici che influiscono sul passaggio di
clienti?
I dati raccolti sono contenuti nel foglio di lavoro Original del file Creditunion.xlsx, visualizzato
nella figura 54-1 della pagina successiva. Se si prova a eseguire una regressione su questi dati
utilizzando variabili fittizie (come descritto nel capitolo 48, “Integrazione di fattori qualitativi
nella regressione multipla”), in cui la variabile dipendente è il numero di clienti che arrivano
ogni giorno (dati della colonna E). Sarebbero necessarie 19 variabili indipendenti:
❑
11 per considerare il mese (12 mesi meno 1)
❑
4 per considerare il giorno della settimana (5 giorni lavorativi meno 1)
❑
2 per considerare i tipi di giorni di pagamento che si verificano ogni mese
❑
2 per considerare il fatto che un particolare giorno segua o preceda una vacanza
Microsoft Office Excel 2007 consente solo 15 variabili indipendenti, perciò questo l’approccio
appare problematico.
437
Excel.book Page 438 Saturday, February 28, 2009 6:53 PM
438
Microsoft Office Excel 2007 Analisi dei dati
Figura 54-1 Dati utilizzati per vedere il passaggio di clienti alla Credit Union
Quando un modello previsione di regressione richiede più di 15 variabili indipendenti, si può
utilizzare la funzionalità Risolutore di Excel per stimare i coefficienti delle variabili
indipendenti. Si può anche utilizzare Excel per calcolare i valori R-quadro tra le previsioni e
l’effettivo passaggio di clienti e la deviazione standard degli errori di previsione. Per analizzare
questi dati, ho creato un’equazione di previsione utilizzando una tabella di ricerca per “cercare”
il giorno della settimana, il mese e altri fattori. Quindi ho utilizzato il Risolutore per scegliere i
coefficienti per ogni livello di ciascun fattore che produce la somma minima di errori quadratici
(per ogni giorno, l’errore è uguale al numero di clienti effettivi meno il numero di clienti
previsti). Ecco i particolari.
Ho iniziato con il creare le variabili per gli indicatori (nelle colonne da G a J) per determinare
se il giorno prevede pagamenti del personale (SP), della facoltà (FAC), è prima di una vacanza
(BH) o è dopo una vacanza (AH) (vedere la figura 54-1). Ad esempio, nelle celle G4, H4 e J4
ho immesso 1 per indicare che il 2 gennaio era giorno di pagamento del personale, giorno di
pagamento della facoltà e cadeva dopo una vacanza. La cella I4 contiene 0 per indicare che il 2
gennaio non cadeva prima di una vacanza.
La nostra previsione viene definita da una costante (che aiuta a centrare le previsioni in modo
che siano più precise) e gli effetti per ogni giorno della settimana, per ogni mese, per un giorno
di pagamento del personale, per un giorno di pagamento della facoltà, per un giorno che cade
prima di una vacanza e per un giorno che cade dopo una vacanza. Ho inserito valori di prova
per tutti questi parametri (celle variabili del Risolutore) nell’intervallo di celle O4:O26,
visualizzato nella figura 54-2. Il Risolutore sceglierà quindi i valori che faranno in modo che il
modello aderisca meglio ai dati. Per ogni giorno, la previsione del numero di cliente sarà
generata dalla seguente equazione:
Excel.book Page 439 Saturday, February 28, 2009 6:53 PM
Capitolo 54
Previsioni in presenza di eventi speciali
439
Numero clienti previsti=Costante+(Effetto mese)+(Effetto giorno della
settimana)+(Eventuale effetto giorno pagamento personale)+(Eventuale effetto giorno
pagamento facoltà)+(Eventuale effetto prima di vacanza)+(Eventuale effetto dopo
vacanza)
Utilizzando questo modello, si calcola una previsione per il numero di clienti di ogni giorno
copiando da K4 a K5:K257 la formula
$O$26+CERCA.VERT(B4;$N$14:$O$25;2)+CERCA.VERT(D4;$N$4:$O$8;2)
+G4*$O$9+H4*$O$10+I4*$O$11+J4*$O$12
La cella O26 contiene il termine costante. CERCA.VERT(B4;$N$14:$O$25;2) raccoglie il
coefficiente del mese per il mese attuale e CERCA.VERT(D4;$N$4:$O$8;2) raccoglie il
coefficiente del giorno della settimana per la settimana attuale.
G4*$O$9+H4*$O$10+I4*$O$11+J4*$O$12 raccoglie gli (eventuali) effetti che si hanno se il
giorno attuale è SP, FAC, BH o AH.
Copiando da L4 a L5:L257 la formula (E4-K4)^2, si calcola l’errore quadratico per ogni giorno.
Quindi, nella cella L2, si calcola la somma degli errori quadratici con la formula
SOMMA(L4:L257).
Figura 54-2 Celle variabili e previsioni dei clienti
Nella cella R4 si calcola la media delle celle variabili del giorno della settimana con la formula
MEDIA(O4:O8), mentre nella cella R5 si calcola la media delle celle variabili del giorno del mese
con la formula MEDIA(O14:O25) Più avanti, si vincolerà l’effetto sul giorno medio del mese e
della settimana in modo che sia uguale a 0, garantendo così che un giorno del mese o della
settimana con effetto positivo abbia un numero di clienti superiore alla media e un giorno del
mese o della settimana con effetto negativo abbia un numero di clienti inferiore alla media.
Excel.book Page 440 Saturday, February 28, 2009 6:53 PM
440
Microsoft Office Excel 2007 Analisi dei dati
Si possono utilizzare le impostazioni del Risolutore visualizzate nella figura 54-3 della pagina
successiva per scegliere i parametri di previsione in modo da minimizzare la somma degli errori
quadratici.
Figura 54-3 La finestra di dialogo Parametri del Risolutore per la determinazione di
parametri della previsione
Il modello del Risolutore modifica i coefficienti per mese, giorno della settimana, BH, AH, SP,
FAC e costante in modo da minimizzare la somma dagli errori quadratici. Si vincola anche
l’effetto del giorno medio della settimana e del mese in modo che sia uguale a 0. Utilizzando il
Risolutore, si ottengono i risultati visualizzati nella figura 54-2. Ad esempio, si trova che il
venerdì è il giorno della settimana con il maggiore passaggio di clienti e il giugno è il mese con
più passaggi di clienti. Un giorno di pagamento del personale innalza la previsione (lasciando
immutati gli altri fattori; ceteris paribus in latino) di 397 clienti.
Come è possibile valutare la precisione di una previsione?
Per valutare la precisione della previsione, nella cella J1 si calcola il valore R-quadro tra le
previsioni e il numero di clienti effettivo. La formula utilizzata è RADQ(E4:E257;K4:K257)
Questa formula calcola la percentuale della variazione effettiva nel numero dei clienti, spiegata
nel modello previsionale. Si trova che le variabili indipendenti spiegano il 77% della variazione
giornaliera del numero di clienti.
L’errore per ogni giorno viene calcolato nella colonna M, copiando da M4 a M5:M257 la
formula E4-K4. Un’approssimazione vicina all’errore standard della previsione viene data dalla
deviazione standard degli errori. Questo valore viene calcolato nella cella M1 utilizzando la
formula DEV.ST(M4:M257) In tal modo, circa il 68% delle previsioni dovrebbe essere preciso
entro 163 clienti, il 95% dovrebbe essere preciso entro 326 clienti e così via.
Proviamo a individuare gli elementi esterni. Si ricordi che un’osservazione è un elemento
esterno se il valore assoluto dell’errore di previsione supera di due volte l’errore standard della
regressione. Selezionare l’intervallo M4:M257 e quindi fare clic su Formattazione condizionale
nella scheda Inizio. Successivamente, selezionare Nuova regola e, nella finestra di dialogo
Nuova regola di formattazione, scegliere Utilizzare una formula per specificare i criteri di
formattazione. Completare la descrizione della regola nella finestra di dialogo, come mostrato
nella figura 54-4 (per ulteriori informazioni sulla formattazione condizionale, vedere il
capitolo 22, “Formattazione condizionale”).
Excel.book Page 441 Saturday, February 28, 2009 6:53 PM
Capitolo 54
Previsioni in presenza di eventi speciali
441
Figura 54-4 Utilizzo della formattazione condizionale per evidenziare gli elementi esterni
Dopo avere scelto un formato con carattere rosso, le impostazioni di formattazione
condizionale visualizzeranno in rosso qualsiasi errore che supera 2* (deviazione standard degli
errori) come errore assoluto. Guardando gli elementi esterni, si trova che spesso il numero dei
clienti nei primi tre giorni del mese viene sottostimato. Inoltre, durante la seconda settimana di
marzo (interruzione primaverile), viene sovrastimato il numero e il giorno prima
dell’interruzione primaverile lo si sovrastima abbondantemente.
Per rimediare a questo problema, nel foglio di lavoro 1st Three Days sono state aggiunte celle
variabili per ognuno dei primi tre giorni del mese, per l’interruzione primaverile e per il giorno
che precede l’interruzione primaverile. Sono stati aggiunti valori di prova per questi nuovi
effetti nelle celle O26:O30. Copiando da K4 a K5:K257 la formula
$O$25+CERCA.VERT(B4;$N$13:$O$24;2)+CERCA.VERT(D4;$N$4:$O$8;2)+G4*$O$9+H4*
$O$10+I4*$O$11+J4*$O$12+SE(C4=1;$O$26;SE(C4=2;$O$27;SE(C4=3;$O$28;0)))
si includono gli effetti dei primi tre giorni del mese. (Il termine SE(C4=1;$O$26);SE(C4=2;$O$27;
SE(C4=3;$O$28;0))) raccoglie l’effetto dei primi tre giorni del mese). I coefficienti per
l’interruzione di primavera sono stati immessi manualmente nelle celle K54:K57. Ad esempio,
nella cella K52 è stato aggiunto +O29 alla formula e nelle celle K53:K57 è stato aggiunto +O30.
Dopo avere incluso le nuove celle variabili nella finestra di dialogo Risolutore, si trovano i
risultati visualizzati nella figura 54-5 della pagina successiva. Notare che i primi tre giorni del
mese aumentano di molto il numero dei clienti (probabilmente a causa degli aiuti governativi e
degli assegni della Previdenza Sociale) e che l’interruzione di primavera riduce il numero di
clienti. La figura 54-5 visualizza anche il miglioramento nella precisione della previsione. Il
valore R-quadro (RQ) è migliorato all’87% e ha ridotto l’errore standard a 122 clienti.
Excel.book Page 442 Saturday, February 28, 2009 6:53 PM
442
Microsoft Office Excel 2007 Analisi dei dati
Figura 54-5 Parametri delle previsioni e previsioni che includono l’interruzione di primavera
e i primi tre giorni del mese
Osservando gli errori di previsione per la settimana dal 24/12 al 31/12 (vedere la figura 54-6), si
vede che il numero di clienti per i giorni di quella settimana è stato notevolmente sovrastimato.
È stato anche sottostimato il numero di clienti della settimana prima di Natale. Un ulteriore
esame degli errori di previsione (spesso chiamati residui) ci mostra anche le seguiti particolarità:
❑
Il Giorno del Ringraziamento è diverso da una vacanza normale in quanto dalla Credit Union
passano di gran lunga meno clienti di quelli previsti per il giorno dopo il Ringraziamento.
❑
Nel giorno prima del Venerdì Santo passa un gran numero di clienti poiché le persone
lasciano la città per la Pasqua.
❑
Anche nella scadenza fiscale (16 aprile) c’è più clientela del previsto.
❑
La settimana prima che inizino i corsi autunnali alla Indiana University (ultima settimana
di agosto) non c’era molta clientela, probabilmente poiché gran parte del personale e dei
docenti si concede una “rapida vacanza estiva” prima della frenetica attività del semestre
autunnale.
Figura 54-6 Errori della settimana di Natale
Excel.book Page 443 Saturday, February 28, 2009 6:53 PM
Capitolo 54
Previsioni in presenza di eventi speciali
443
Nel foglio di lavoro Final mode, ho aggiunto le celle variabili per incorporare gli effetti di questi
fattori. Dopo avere aggiunto i nuovi parametri delle celle variabili, si è eseguito nuovamente il
Risolutore. I risultati vengono visualizzati nella figura 54-7. Il valore RQ è salito al 92% e l’errore
standard è sceso a 98,61 clienti! Si noti che nella settimana successiva al Natale il numero
giornaliero di clienti si è ridotto di 359; il giorno prima del Ringraziamento si sono aggiunti 607
clienti; il giorno dopo il Ringraziamento il numero di clienti si è ridotto di 161, e così via.
Figura 54-7
Parametri della previsione finale
Notare come è migliorato il modello di previsione utilizzando gli elementi esterni. Se gli elementi
esterni hanno qualcosa in comune (come ad esempio i primi tre giorni del mese), si può includere
il fattore comune come variabile indipendente e l’errore di previsione sarà ridotto.
Come è possibile controllare se gli errori di previsione sono casuali?
Un buon metodo di previsione dovrebbe creare errori o residui di previsione casuali. Per gli
errori casuali, si intende che gli errori non mostrano alcun modello distinguibile. Se gli errori di
previsione sono casuali, il segno degli errori dovrebbe cambiare (da più a meno o da meno a
più) circa la metà delle volte. Quindi, un test comunemente utilizzato per valutare la casualità
degli errori di previsione consiste nel guardare il numero di cambiamenti di segno negli errori.
Se si hanno n osservazioni, la non casualità degli errori è indicata dal fatto che si trovino meno
n–1
2
–
n
+
n
o più
n–1
2
Excel.book Page 444 Saturday, February 28, 2009 6:53 PM
444
Microsoft Office Excel 2007 Analisi dei dati
cambiamenti di segno. Nel foglio di lavoro Final Model, mostrato nella figura 54-8, ho
determinato il numero di cambiamenti di segno nei residui copiando dalla cella P5 a P6:P257 la
formula SE(M5*M4<0;1;0). Un cambiamento di segno nei residui avviene se e solo se il
prodotto di due residui consecutivi è negativo. Quindi la nostra formula produce 1 ogni volta
che si verifica un a cambiamento di segno nei residui. Ci sono 125 cambiamenti di segno. Nella
cella P1, ho calcolato
254 – 1
2
–
254 = 110.6
i cambiamenti di segno come discriminante dei residui non casuali. Quindi nel nostro caso si
hanno residui casuale.
Figura 54-8
Determinazione della casualità dei residui
È stata condotta un’analisi simile per prevedere il numero giornaliero di clienti che arrivano per
la cena in una grande catena di ristoranti. I fattori speciali corrispondevano alle vacanze. Si è
trovato che nel Super Sunday (il giorno del Super Bowl di football) era il giorno con meno
clienti, mentre San Valentino e la Festa della Mamma erano i più affollati. Inoltre, il sabato era
il giorno più affollato della settimana per la cena e il venerdì era il giorno più affollato della
settimana per il pranzo.
Problemi
1. Come si possono utilizzare le tecniche descritte in questo capitolo per predire le vendite
giornaliere di penne nel negozio Staples?
2. Avendo alcuni anni di dati, come si potrebbe incorporare una tendenza nell’analisi?
Excel.book Page 445 Saturday, February 28, 2009 6:53 PM
Capitolo 55
Introduzione alle variabili casuali
■
Che cos’è una variabile casuale?
■
Che cos’è una variabile casuale discreta?
■
Che cosa sono la media, la varianza e la deviazione standard di una variabile casuale?
■
Che cos’è una variabile casuale continua?
■
Che cos’è una funzione densità di probabilità?
■
Che cosa sono le variabili casuali indipendenti?
Nel mondo di oggi, l’unica cosa certa è che si devono affrontare molte incertezze. Nei nove capitoli
successivi verranno illustrate alcune potenti tecniche che è possibile utilizzare per tener conto
dell’incertezza nei modelli aziendali. Il componente chiave per integrare l’incertezza nella
modellazione è la comprensione dell’utilizzo delle variabili casuali.
Che cos’è una variabile casuale?
Qualsiasi situazione il cui risultato è incerto viene chiamata esperimento. Il valore di una variabile
casuale è basato sul risultato (incerto) di un esperimento. Ad esempio, lanciare una coppia di
dadi è un esperimento e una variabile casuale potrebbe essere definita come la somma dei valori
dei dadi. In questo caso, la variabile casuale potrebbe assumere uno qualunque dei valori 2, 3, e
così via, fino a 12. Come altro esempio, si consideri come esperimento la vendita di una nuova
console per videogiochi, per cui una variabile casuale potrebbe essere definita come la quota di
mercato di questo nuovo prodotto.
Che cos’è una variabile casuale discreta?
Una variabile casuale è discreta se può assumere un numero limitato di valori possibili. Ecco
alcuni esempi di variabili casuali discrete:
❑
Numero di concorrenti potenziali del proprio prodotto
❑
Numeri di assi estratti in una mano di poker a cinque carte
❑
Numero di incidenti automobilistici in cui si è coinvolti in un anno (speriamo 0!)
❑
Numero di punti che si vedono su un dado
❑
Numero di tiri liberi su 12 che Steve Nash realizza durante una partita di pallacanestro
445
Excel.book Page 446 Saturday, February 28, 2009 6:53 PM
446
Microsoft Office Excel 2007 Analisi dei dati
Che cosa sono la media, la varianza e la deviazione standard di una variabile casuale?
Nel capitolo 37, “Riepilogo dei dati mediante le statistiche descrittive”, sono state illustrate la
media, la varianza e la deviazione standard di una serie di dati. Sostanzialmente, la media di una
variabile casuale (spesso indicata con µ) è il valore medio della variabile casuale che ci si
attenderebbe se si eseguisse molte volte un esperimento. La media di una variabile casuale viene
detta spesso valore previsto della variabile casuale. La varianza di una variabile casuale (spesso
indicata da σ2) è il valore medio della deviazione quadratica dalla media di una variabile casuale,
che ci si attenderebbe se si eseguisse molte volte l’esperimento. La deviazione standard di una
variabile casuale (spesso indicata con σ) è semplicemente la radice quadrata della varianza.
Come accade con le serie di dati, la media di una variabile casuale è una misura sintetica del
valore tipico della variabile casuale, mentre la varianza e la deviazione standard misurano la
diffusione della variabile casuale rispetto alla sua media.
Come esempio di calcolo della media, della varianza e della deviazione standard di una variabile
casuale, si supponga di ritenere che il rendimento del mercato mobiliare nel prossimo anno sia
governato dalle seguenti probabilità:
Probabilità
Rendimento del mercato
.40
+20%
.30
0%
.30
-20%
Effettuando i calcoli a mano si ottiene quanto segue:
µ=0,40*(0,20)+0,30*(0,00)+0,30*(-0,20)=0,02 o 2%
σ2=0,4*(0,20-0,02)2+0,30*(0,0-0,02)2+0,30*(-0,20-0,02)2=0,0276
Quindi σ=0,166 o 16,6%.
Nel file Meanvariance.xlsx (visualizzato nella figura 55-1) ho verificato questi calcoli.
Figura 55-1 Calcolo della media, della deviazione standard e della varianza di una variabile
casuale
Ho calcolato la media del rendimento del mercato nella cella C9 con la formula
=MATR.SOMMA.PRODOTTO(B4:B6;C4:C6). Questa formula moltiplica ogni valore della
variabile casuale per la sua probabilità e somma i prodotti.
Excel.book Page 447 Saturday, February 28, 2009 6:53 PM
Capitolo 55
Introduzione alle variabili casuali
447
Per calcolare la varianza del rendimento del mercato, ho determinato la deviazione quadratica
di ogni valore della variabile casuale dalla media copiando da D4 a D5:D6 la formula =(B4)($C$9)^2. Quindi, nella cella C10 ho calcolato la varianza del rendimento del mercato come
deviazione quadratica media dalla media, con la formula =MATR.SOMMA.PRODOTTO
(C4:C6;D4:D6). Infine ho calcolato la deviazione standard del rendimento del mercato nella
cella C11, con la formula =RADQ(C10).
Che cos’è una variabile casuale continua?
Una variabile casuale continua è una variabile casuale che può assumere un valore molto grande
o, in qualsiasi caso, un numero infinito di valori. Ecco alcuni esempi di variabili casuali continue:
❑
Prezzo delle azioni Microsoft tra un anno
❑
Quota di mercato di un nuovo prodotto
❑
Dimensione del mercato di un nuovo prodotto
❑
Costo di sviluppo di un nuovo prodotto
❑
Peso di un neonato
❑
QI di una persona
❑
Percentuale dei tiri da tre punti realizzati da Dirk Nowitzki durante la prossima stagione
Che cos’è una funzione densità di probabilità?
Una variabile casuale discreta può essere specificata da un elenco di valori e dalla probabilità che
si verifichi ciascun valore della variabile casuale. Poiché una variabile casuale continua può
assumere un numero infinito di valori, non è possibile elencare la probabilità che si verifichi
ciascun valore della variabile casuale continua. Una variabile casuale continua è descritta
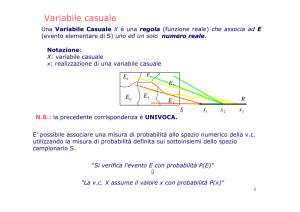
completamente dalla relativa funzione densità di probabilità. Ad esempio, la funzione densità di
probabilità per il QI di una persona scelta a caso viene visualizzata nella figura 55-2.
Figura 55-2 Funzione densità di probabilità per i QI
Excel.book Page 448 Saturday, February 28, 2009 6:53 PM
448
Microsoft Office Excel 2007 Analisi dei dati
Una funzione densità di probabilità (pdf) ha le seguenti proprietà:
❑
Il valore della pdf è sempre maggiore o uguale a 0.
❑
L’area sotto la pdf è uguale a 1.
❑
L’altezza della funzione di densità per un valore x della variabile casuale è proporzionale
alla verosimiglianza che la variabile casuale assume un valore prossimo a x. Ad esempio,
l’altezza della densità per un QI pari a 83 è approssimativamente la metà dell’altezza della
densità per un QI pari a 100. Questo ci dice che i QI prossimi a 83 hanno circa la metà
delle probabilità rispetto ai QI prossimi a 100. Inoltre, poiché la densità raggiunge il
valore massimo a 100, i QI prossimi a 100 sono i più probabili.
❑
La probabilità che una variabile casuale continua assuma un intervallo di valori è uguale
all’area corrispondente sotto la funzione di densità. Ad esempio, la frazione di persone
che hanno un QI compreso tra 80 e 100 è semplicemente l’area sotto la densità compresa
tra 80 a 100.
Che cosa sono le variabili casuali indipendenti?
Le variabili casuali in un insieme sono indipendenti se la conoscenza del valore di uno
qualunque dei loro sottoinsiemi non ci fornisce alcuna informazione sui valori delle altre
variabili casuali. Ad esempio, il numero di partite vinta dalla squadra di football della Indiana
University in un anno è indipendente dalla percentuale di rendimento di Microsoft nello stesso
anno. Sapere che la squadra dell’Indiana si è comportata molto bene non modificherebbe la
nostra percezione del rendimento delle azioni Microsoft durante l’anno.
Invece, i rendimenti delle azioni Microsoft e delle azioni Intel non sono indipendenti. Se
sappiamo che le azioni Microsoft ha avuto un rendimento elevato in un anno, molto
probabilmente le vendite di computer sono state alte e, molto probabilmente, l’anno è stato
positivo anche per Intel.
Problemi
1. Identificare le seguenti variabili casuali come discrete o continue:
❑
Numero di partite che Kerry Wood vince nella prossima stagione con i Chicago Cubs
❑
Numero che esce quando si fa girare la roulette
❑
Vendite di unità PC Tablet nel prossimo anno
❑
Durata di una lampadina prima di bruciare
2. Calcolare la media, la varianza e la deviazione standard del numero di puntini che appaiono
quando si lancia un dado.
Excel.book Page 449 Saturday, February 28, 2009 6:53 PM
Capitolo 55
Introduzione alle variabili casuali
449
3. Determinare se le seguenti variabili casuali sono indipendenti:
❑
Temperatura e vendite giornaliere di un banco di gelati
❑
Segno e numero di una carta estratta da un mazzo di carte da gioco
❑
Inflazione e rendimento del mercato mobiliare
❑
Prezzo di vendita e numero di unità vendute di un’automobile
4. Il prezzo attuale delle azioni di una società è $20. È in corso una scalata alla società. Se la scalata
ha successo, la quotazione azionaria della società aumenterà a $30. Se la scalata non riesce, la
quotazione azionaria scenderà a $12. Determinare l’intervallo di valori della probabilità di
successo della scalata, che renderebbe vantaggioso acquistare oggi l’azione. Si supponga che
l’obiettivo sia massimizzare l’utile previsto. Suggerimento: Utilizzare il comando Ricerca
obiettivo di Microsoft Office Excel 2007, discusso dettagliatamente nel capitolo 16, “Il
comando Ricerca obiettivo”.