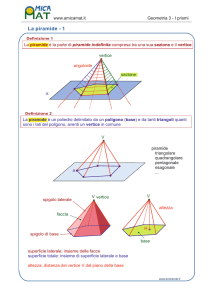
Piramidi
Esercizio guida
Dato un rettangolo ABCD di dimensioni AB
2√2 e BC 2 , tracciare la perpendicolare in A
al piano del rettangolo e indicare con V il punto della retta che ha distanza 2a da A. Calcolare la
misura degli spigoli della piramide VABCD.
8 = 2√3a
(teorema di Pitagora applicato al triangolo VAB)
VB= √4
VC
√94 12 = 4 (teorema di Pitagora applicato al triangolo VAC)
VD 2√2 (VAD triangolo rettangolo isoscele)
1. Una piramide ha per base un triangolo isoscele ABC di lati AB
vertice α = arcos
AC
2 e angolo al
. Sapendo che l’altezza AV misura 3a, calcolare la superficie della
piramide e l’angolo che la faccia VBC forma con il piano di base. [ superficie totale =
;
β = arcos ]
2. Una piramide retta di vertice V ha per base un triangolo equilatero ABC di lato 12a. Calcola
l’altezza e l’apotema della piramide sapendo che lo spigolo AV forma un angolo di 30° con
il piano di base.
[ altezza = 4 a; apotema = 2√7 ]
3. Una piramide retta di vertice V ha per base un quadrato ABCD di lato 4a. Calcola l’altezza e
l’apotema della piramide sapendo che lo spigolo AV forma un angolo di 30° con il piano di
base.
[ altezza = 2
; apotema = 2
]
4. Una piramide retta ha per base un quadrato di perimetro 48a. Sapendo che l’altezza della
piramide è 8a, calcolare la superficie laterale della piramide e l’angolo che le facce laterali
formano con il piano di base. [ 240a2 , α = artg ]
5. Una piramide retta a base quadrata ha apotema che forma un angolo α = artg con il piano
di base. Sapendo che il lato del quadrato misura 8a, calcolare la superficie della piramide. [
144a2 ]
6. Una piramide retta ha per base un quadrato di lato 6a, calcolare la superficie della piramide
sapendo che gli spigoli laterali formano con il piano di base un angolo α = arcsen . [ (36 +
12√41)a2]
7. Una piramide retta ha per base un triangolo equilatero, calcolare la superficie della piramide
sapendo che la sua altezza misura 8a e che le facce laterali formano un angolo α = arctg2
con il piano di base. [48√3 1 √5
]
8. E’ assegnato un triangolo isoscele ABC di lati AB AC 3 e angolo al vertice α =
arcos
. Sulla perpendicolare in A al piano del triangolo sia P il punto in corrispondenza
del quale il piano PBC forma un angolo di 30° con il piano del triangolo. Calcolare la
superficie della piramide PABC. [ 3 3√2 2√6
]
9. Una piramide retta di vertice V ha per base un quadrato ABCD di lato 4a e ha un’altezza
tale che le superfici laterali formano un angolo di 45° con il piano di base. A quale distanza
dal vertice si deve sezionare la piramide con un piano parallelo al piano di base per ottenere
una piramide VA’B’C’D’ che ha superficie pari al 25% di quella della piramide ABCD?
Quanto misurano le due superfici? [ distanza dal vertice = a; A = 16 1 √2 , A’ =
]
4 1 √2
10. Una piramide retta VABC ha per base un triangolo rettangolo ABC che ha il cateto AB =
1 √3
e l’angolo in B di 60°. Calcolare la superficie della piramide sapendo che
l’altezza misura . Qual è l’angolo α che le superfici laterali formano con il piano di base?
[ 1 √3
; α = 60° ]
11. Una piramide retta di vertice V ha altezza h = 3 a e per base un triangolo equilatero di lato
6 a. Calcolare
a) l’apotema della piramide
b) la superficie totale della piramide
c) l’angolo che ciascuna faccia della piramide forma con il piano di base.
[ a) 2√3 ; b) 27√3
; c) 60° ]
Esercizio guida
Una piramide di vertice V ha per base un quadrilatero ABCD che ha area 20 a2 e ha altezza 6a.
Calcolare a quale distanza dal vertice è stato tracciato il piano parallelo al piano di base che stacca
sulla piramide un poligono che ha area 15 a2.
VH’ = x
Per il teorema sulle sezioni parallele di un angoloide vale la proporzione:
20
: 15
6
:
Risolvendo la proporzione si ottiene x2 = 27a2 quindi
x = 3√3 .
12. Una piramide retta ha per base un esagono regolare di lato 4a. Sapendo che l’altezza della
piramide è 2a calcolare la superficie. A distanza dal vertice della piramide tracciare un
piano parallelo al piano di base e indicare con S’ la sezione ottenuta. Calcolare la superficie
della piramide che ha base S’ e vertice V. [ (48+24√3
; (3+ √3
]
13. Una piramide retta a base quadrata ha altezza 4a e le facce laterali formano un angolo α =
artg2 con il piano di base.
a) Calcolare la superficie della piramide.
b) Determinare a quale distanza dal vertice della piramide si deve tracciare un piano
parallelo al piano di base per ottenere una piramide che ha superficie laterale pari al
90% della superficie laterale della piramide assegnata.
[ a) 16 1
√5
2
; b) 6
]
14. Una piramide retta di vertice V ha per base un esagono regolare; l’apotema della piramide
misura 10a e forma un angolo α =arcsen con il piano di base. Calcolare la superficie della
piramide e l’angolo che ciascuno spigolo forma con il piano di base. Ricavare a quale
distanza dal vertice V si deve condurre un piano parallelo al piano di base per ottenere una
piramide la cui superficie laterale è metà di quella della piramide assegnata.
[ superficie = 192√3 , β= artg , distanza dal vertice = 4√2 ]
√
15. Un rettangolo ABCD ha i lati AB = 8 a e BC = 6 a; indicare con V il punto sulla retta
perpendicolare in B al piano del rettangolo tale che VB = 10 a.
a) Calcolare gli angoli che gli spigoli VB, VC, VD formano il piano di base della piramide
VABCD
b) Tracciato un piano α parallelo al piano di base e distante 5√2a dal vertice della
piramide, calcolare l’area della sezione staccata sulla piramide.
[ a) α = artg , γ
, δ=
; b) 24
]