ESAME di STATO 2001
Sessione suppletiva
Disegni a cura del prof. Cristiano DOMENICHELLI
Testi della prof.ssa Tiziana LA TORELLA
LICEO SCIENTIFICO “GALILEO FERRARIS”
ESAME DI STATO DI LICEO SCIENTIFICO
CORSO DI ORDINAMENTO
Sessione 2001
suppletiva
Indirizzo: SCIENTIFICO
Tema di: MATEMATICA
Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario.
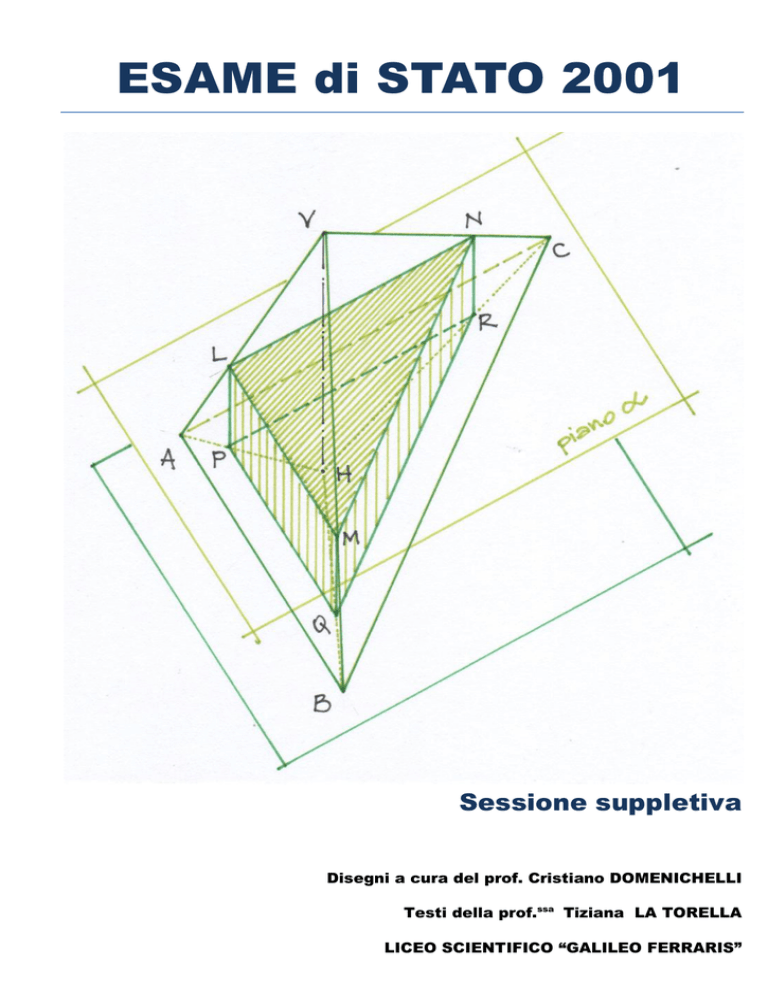
PROBLEMA 2
Una piramide retta, di vertice V, ha per base il triangolo ABC, rettangolo in A , la cui area è
dove
è una lunghezza assegnata. Si sa inoltre che
piramide forma con il piano della base ABC un angolo
,
e che il piano della faccia VAB della
tale che il
.
a) Calcolare l’altezza della piramide.
b) Controllato che essa è
, calcolare la distanza del vertice C dal piano della faccia VAB.
c) Condotto , parallelamente alla base ABC , un piano che sechi la piramide e considerato il
prisma retto avente una base coincidente con il triangolo sezione e per altezza la distanza di
dalla base ABC, calcolare per quale valore di tale distanza il prisma ha volume massimo.
d) Il prisma di volume massimo ha anche la massima area totale?
Breve introduzione:
Il problema è diviso in quattro parti e chiede :
a) la misura dell’altezza h della piramide, relativa alla base ABC quindi la ricerca del triangolo
rettangolo avente h come cateto verticale, noto l’angolo opposto al cateto h;
b) la misura dell’altezza h’ della piramide, relativa alla base ABV, noti il volume della piramide e la
superficie di ABV;
c) il volume del prisma , nota la proporzionalità tra altezza e base della piramide maggiore e
altezza e base della piramide minore;
d) la superficie totale massima.
Una piramide retta, di vertice V, ha per base il triangolo ABC, rettangolo in A , la cui area è
, dove
è una lunghezza assegnata. Si sa inoltre che
VAB della piramide forma con il piano della base ABC un angolo
e che il piano della faccia
tale che il
a) Calcolare l’altezza della piramide.
Data la relazione
, si calcolano nel triangolo ABC le misure dei cateti AB e AC e
dell’ipotenusa BC.
, per il teorema di Pitagora
.
Nota l’area del triangolo ABC,
, si calcolano i lati :
Per il teorema delle tre perpendicolari :
“Dal piede (H) di una perpendicolare (VH) ad un piano (ABC) , si traccia la perpendicolare HT
ad una qualsiasi retta (AB) del piano, quest’ultima (AB) risulta perpendicolare al piano
individuato da VH e HT”.
Il segmento HT, perpendicolare al lato AB, è anche raggio R del cerchio inscritto nel triangolo
rettangolo ABC :
.
Il triangolo VHK è rettangolo, per il teorema fondamentale della trigonometria
.
i teoremi sui triangoli rettangoli
L’altezza della piramide misura
.
punto a)
b) Controllato che essa è
, calcolare la distanza del vertice C dal piano della faccia VAB
La distanza del vertice C dalla faccia AVB è l’altezza CK=
della piramide.
relativa alla base ABV
Per determinare l’altezza della piramide relativa alla base ABV , si calcola il volume
della piramide e la superficie della base ABV .
Distanza tra il vertice C e la faccia VAB :
punto b)
c) Condotto , parallelamente alla base ABC , un piano che sechi la piramide e considerato
il prisma retto avente una base coincidente con il triangolo sezione e per altezza la
distanza di dalla base ABC, calcolare per quale valore di tale distanza il prisma ha
volume massimo.
Sia
la distanza tra il vertice V della piramide e il piano
, l’altezza del prisma è
Si considera la proporzionalità tra le due piramidi simili ABCV e LMNV:
punto c)