2 Numeri reali
M. Simonetta Bernabei &
Horst Thaler
Numeri interi positivi o
Naturali
0
1
2
3
Con i numeri Naturali è sempre
possibile fare l’addizione e la
moltiplicazione p.es.: 5+2 = 7; 3*4 = 12;
ma non sempre la sottrazione p. es.: 78 = -1.
Per poter effettuare sempre anche la
sottrazione occorre ampliare i n.
Naturali aggiungendo anche i numeri
interi negativi… -1 –2 –3 –4 …
4
…
Insieme numerico
+
*
Si
-
No
:
No
Si
Numeri interi con segno
o Relativi
Numeri interi positivi
o Naturali
…
-4
-3
-2
-1
0
1
Con i numeri interi Relativi è sempre
possibile fare l’addizione, la
moltiplicazione e la sottrazione p.es.:
5+3 = 8; 3*4 = 12; 7-8 = -1 ; ma non
sempre la divisione p.es.: 3/2 = 1,5
Per poter effettuare sempre anche la
divisione occorre ampliare i n. interi
Relativi aggiungendo anche tutte le
altre possibili frazioni mn
2
3
4
…
Insieme numerico
+
*
:
Si
Si
Si
No
I numeri Naturali
ampliati con i
numeri interi
relativi e
successivamente
con tutti i numeri
esprimibili sotto…
forma d frazione…
vengono detti
numeri Razionali
Insieme
numerico
+
*
:
Si
Si
Si
Si
Numeri esprimibili
come frazioni o
Razionali
Numeri interi positivi
o Naturali
-4
-3
-2
-1
0
1
2
m
n
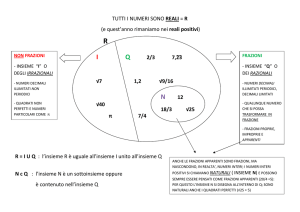
Tutti i numeri sono
esprimibili sotto forma di
frazione eccetto i numeri
decimali illimitati
aperiodici che vengono
detti Irrazionali
3
4
…
Numeri
decimali
illimitati
aperiodici o
Irrazionali
2
e
Numeri Reali
Numeri
Razionali
Numeri Naturali
NumeriRelativi
…
-4 -3
-2
-1
0
1
2
3
m
n
Tutti i numeri sono esprimibili sotto
forma di frazione eccetto i numeri
decimali illimitati aperiodici che
vengono detti Irrazionali
4
…
Numeri
decimali
illimitati
aperiodici o
Irrazionali
2
e
I Numeri interi positivi o Naturali sulla retta
orientata: la retta è in realtà una semiretta
costituita da un numero discreto di punti.
6 7 8 9 …
u
1
0
2
3
4
5
Numeri interi con segno o Relativi sulla retta
orientata (costituita da un numero discreto di
punti)
u
…
-6
-5
-4
-3
-2
-1
0
u
-3
-2
23
-1
21
1
2
4
5
6
7
8
9
…
Numeri esprimibili come frazioni o Razionali
rappresentati sulla Retta orientata : la retta
presenta ancora “buchi” determinati dai numeri
Irrazionali
1
0
1
2
3 13
e
2
2
4
Numeri Reali: Razionali ed Irrazionali sulla
retta reale; i numeri Reali “coprono”, in
modo continuo, tutti i punti della retta
orientata.
u
-3
3
-2
23
-1
21
0
1
2
1
2
2
e
3
13
4
Rappresentazione decimale di un reale
Numero periodico semplice
Numero periodico misto
Numero reale irrazionale
Corrispondenza biunivoca tra retta
e numeri reali
• Esiste una corrispondenza biunivoca tra l’
insieme dei numeri reali e i punti della retta:
ad ogni numero reale corrisponde uno ed un
solo punto sulla retta e viceversa ad ogni
punto della retta corrisponde un solo numero
reale.
Le operazioni in R
L’addizione, la sottrazione, la
moltiplicazione, la divisione e la radice
ennesima con radicando positivo sono
operazioni ben definite in R (il risultato
è sempre un numero reale)
La radice non è ancora ben
definita:
in alcuni casi non si può eseguire
• La radice pari di un reale
negativo non si può eseguire in
R: 2
4
7
Proprietà delle operazioni: commutativa
Proprietà delle operazioni: associativa
Proprietà Distributiva
• Proprietà distributiva della moltiplicazione
rispetto alla somma. Per ogni a,b,c in R
ab c ab ac
32 5 3 2 3 5
Elemento neutro della somma
• Esiste un unico numero, 0, tale che
preserva l’ identità rispetto alla somma.
a+0=ae0+a=a
per ogni a in A
• Aggiungendo 0 ad un numero a il
risultato della somma non cambia.
Elemento neutro della moltiplicazione
Inverso rispetto alla somma o
opposto
• Per ogni numero reale a esiste un unico
numero reale –a detto opposto tale che
la loro somma è uguale all’ elemento
neutro 0:
a + (-a) = 0
• In altre parole aggiungendo ad un
numero reale a il suo opposto il
risultato è 0.
Inverso rispetto alla moltiplicazione o
reciproco
• Per ogni numero reale a diverso da 0 esiste
un unico numero reale 1
1
a
a
• detto reciproco tale che il loro prodotto è 1:
1
a 1
a
• In altre parole moltiplicando ad un numero
reale a il suo reciproco il risultato è 1.
Proprietà
(a) a
1
(a ) a
1
a
a b a (b)
1 1
1
a : b a b a
b
1
Proprietà delle operazioni
Proprietà delle operazioni
a R,
a0 0a 0
a, b R,
(a ) b ab
(a ) (b) a b
a, b R : a, b 0
(ab) 1 a 1 b 1
• Legge di annullamento del prodotto: se
a b 0 a 0 _ o _ b 0
Proprietà delle operazioni
• Proprietà invariantiva della divisione:
a, b, c R
• con b, c 0
• si ha
a ac
b bc
Proprietà delle operazioni
• Somma di frazioni:
a, b, c, d R
• con b, d 0
• si ha
a b ad bd
b d
bd
Proprietà delle operazioni
• Prodotto di frazioni:
a, b, c, d R
• con b, d 0
• si ha
a c ac
b d bd
Potenza
Il prodotto di più numeri naturali uguali fra loro si abbrevia
mediante il simbolo di potenza. Se a è un numero reale e n
è un numero naturale maggiore di 1, si pone
a a a… a
se n > 1
n volte
an =
a
se n = 1
1
se n = 0 e a ≠ 0
00 non ha
significato.
27
PROPRIETA’ DELLE POTENZE
Dati a, b R, m, n Z
• 𝑎𝑛 𝑎𝑚 = 𝑎𝑛+𝑚 ,
• 𝑎
•
•
•
•
•
−𝑛
=
1
,
𝑛
𝑎
𝑎𝑛 : 𝑎𝑚 = 𝑎𝑛−𝑚 ,
𝑎: 𝑏 𝑛 = 𝑎𝑛 : 𝑏 𝑛 ,
(𝑎𝑏)𝑛 = 𝑎𝑛 𝑏 𝑛 ,
(𝑎𝑛 )𝑚 = 𝑎𝑛𝑚 ,
𝑎0 = 1,
a0
a0
b0
a0
Ordinamento dei numeri reali
• L’ insieme dei numeri reali R è totalmente
ordinato con la relazione binaria < che soddisfa
• (i) se a,b,c∈R sono tali che a<b e b<c, allora si
ha anche a<c (transitiva).
• (ii) se a<b, allora b non è minore di a
(antisimmetrica).
• (iii) se a, b ∈ R, allora una ed una sola delle
seguenti possibilità si verifica: a < b, oppure
a=b oppure b<a;
Proprietà delle disuguaglianze
a 0
2
Intervalli di R
a
b
[
]
(
)
b
a
a
[
(
]
a
b
)
b
Intervalli di R
]
a
[
a
)
(
a
a
Completezza di R
(Assioma di Dedekind)
• L’ insieme dei numeri reali R munito della
relazione d’ordine < è (ordinalmente)
completo, cioè dati due sottoinsiemi non vuoti
A e B di R tali che
• a≤b per ogni a∈A e per ogni b∈B, esiste un
elemento s ∈ R , detto elemento separatore,
tale che
• a ≤ s ≤ b per ogni a ∈ A e per ogni b ∈ B.
Valore assoluto
• Dato un numero reale 𝑥 si definisce modulo di
𝑥 e si indica con |𝑥| la seguente espressione:
𝑥 per 𝑥 ≥ 0
𝑥 =
−𝑥 per 𝑥 < 0
• Esempi: 2 = 2; −4 = 4