Geometria teoria

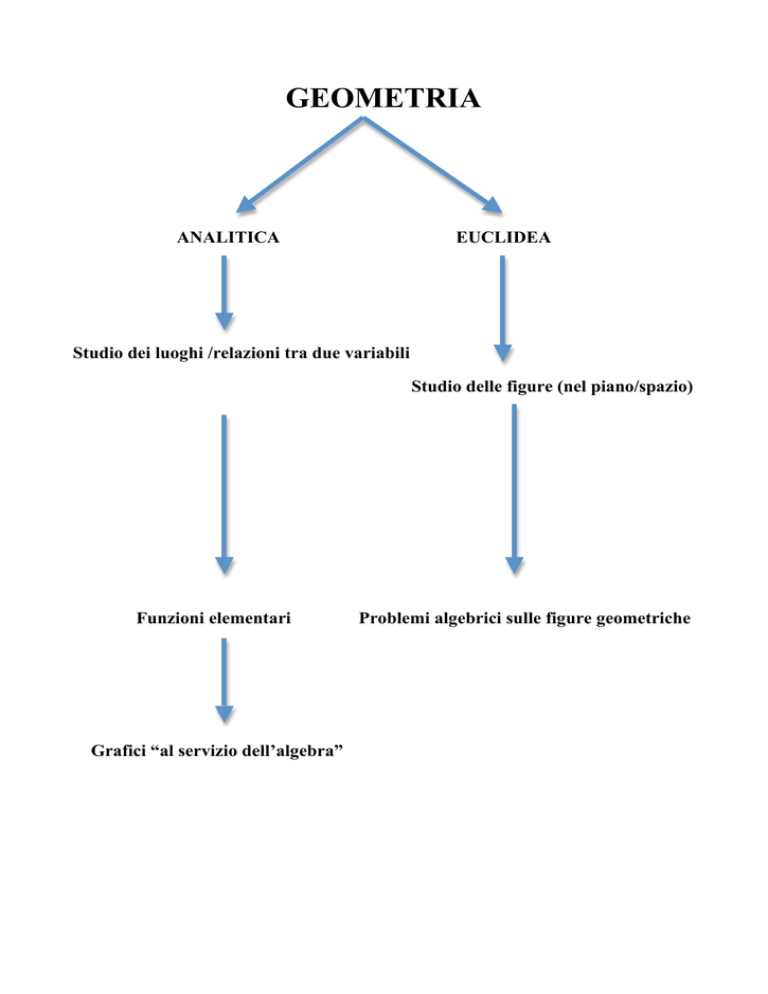
GEOMETRIA
ANALITICA
EUCLIDEA
Studio dei luoghi /relazioni tra due variabili
Studio delle figure (nel piano/spazio)
Funzioni elementari
Grafici “al servizio dell’algebra”
Problemi algebrici sulle figure geometriche
GEOMETRIA ANALITICA
LA RETTA
Equazione esplicita
y = mx + q
m = − a/b ; q = − c/b
r ≡ s ⇔ m1 = m2
q1 = q2
r // s ⇔
q1 ≠ q2
m1 = m2
Equazione implicita
a/a’ = b/b’= c/c’
a/a’ = b/b’≠ c/c’
r ⊥ s ⇔ m1 = − 1/m2 ( m1m2 = −1 )
ab’ – a’b = 0
ac’ – a’c = 0
bc’ – b’c = 0
ab’ – a’b = 0
ac’ – a’c ≠ 0
bc’ – b’c ≠ 0
aa’ + bb’ = 0
fascio per P (x0,y0) :
y – y0 = m( x – x0) ( esclude x = x0 )
retta per 2 punti P0 (x0,y0) P1 (x1,y1)
ax + by + c = 0
a(x – x0) + b(y – y0) = 0 a,b ∈ R
y – y0
____________
y1 – y0
=
x – x0
_____________
x1 – x0
distanza punto P0 (x0,y0) dalla retta :
y0 – (mx0 + q) 
d(P0 , r) =
_______________________
ax0 + by0 + c
d(P0 , r) =
_________________________
CONICHE
Sono rappresentate da equazioni di 2° grado :
ax2 + bxy + cy2 + dx + ey + f = 0 che verificano alcune condizioni.
La quantità Δ = b2 – 4ac ,detta discriminante della conica, le può classificare:
Δ <0
la conica è una circonferenza od un’ellisse
Δ =0
la conica è una parabola
Δ >0
la conica è una iperbole
CIRCONFERENZA
Equazione canonica: ( x –α)2 + (y – β)2 = r2
essendo C(α,β) il centro ed r il raggio
2
2
Equazione generale : x + y + ax + by + c = 0 con le condizioni :
 x2 e y2 hanno lo stesso coefficiente unitario
( o trasformabile in unitario)
 manca il termine xy
 a2 + b2 - 4c >0
LEGAMI FRA I COEFFICIENTI DELLE 2 EQUAZIONI:
a = −2α;
α = − a/2
b = −2β
β = − b/2
se α2 + β2 − c < 0 la circonferenza è degenere
c = α2 + β2 − r2
r=
se α2 + β2 − c = 0 la circonferenza si riduce al
r=
centro C.
PARABOLA
Parabola con asse di simmetria // asse y:
y = ax2 + bx + c
Parabola con asse di simmetria // asse x:
x = ay2 + by + c
SIGNIFICATO DEI PARAMETRI
a = concavità della curva
a > 0 → concavità verso l’alto
a > 0 → concavità verso destra
a < 0 → concavità verso il basso
a < 0 → concavità verso sinistra
b = traslazione asse di simmetria
b = 0 → asse ≡ asse y
b = 0 → asse ≡ asse x
ab>0 → asse traslato a sinistra dell’asse y
ab>0 → asse traslato sotto l’asse x
ab<0 → asse traslato a destra dell’asse y
ab<0 → asse traslato sopra l’asse x
c = traslazione verticale della curva= intersezione curva con asse // asse di simmetria
c = 0 → curva passa per origine
c = 0 → curva passa per origine
c >0 → curva interseca asse y sopra origine
c >0 → curva interseca asse x a destra origine
c < 0 → curva interseca asse y sotto origine
c < 0 → curva interseca asse x a sinistra origine
Elementi importanti
asse simmetria → x = −b/2a
asse simmetria → y = −b/2a
vertice → V( −b/2a, − Δ/4a)
vertice → V(− Δ/4a ,−b/2a)
fuoco
→ F(−b/2a, (1− Δ)/4a)
fuoco
→ F((1− Δ)/4a ,−b/2a)
direttrice → y = −(1+ Δ)/4a
direttrice → x = −(1+ Δ)/4a
ELLISSE
Ellisse con i fuochi sull’asse x
Ellisse con i fuochi sull’asse y
a>b
fuochi
→ F(±
Asse x = asse maggiore
b>a
, 0)
fuochi
→ F(0 , ±
Asse y = asse maggiore
)
eccentricità → e = c/a essendo c =
eccentricità → e = c/b essendo c =
quindi
quindi
se a = b → l’ellisse si riduce alla circonferenza di centro l’origine e raggio a
IPERBOLE
Iperbole con i fuochi sull’asse x:
fuochi
→ F(±
Asse x = asse trasverso
, 0)
fuochi
→ F(0, ±
Asse y = asse trasverso
eccentricità → e = c/a essendo c =
quindi e > 1
asintoti
→ y = ± b/a x
asintoti
Iperbole con i fuochi sull’asse y:
)
eccentricità → e = c/b essendo c =
quindi e > 1
asintoti
→ y = ± b/a x
Iperbole equilatera
→y=± x
asintoti
→y=± x
Iperbole equilatera riferita ai propri asintoti:
k > 0 iperbole nel 1° e 3° quadrante
xy = k
k < 0 iperbole nel 2° e 4° quadrante
Funzione omografica
c≠0
y=
altrimenti y = a/d x + b/d retta
con
ad – bc ≠ 0 altrimenti y = a/c e x ≠ - d/c retta // asse x privata di un punto
coincide con iperbole equilatera di centro C ( −d/c, a/c) e asintoti paralleli agli assi cartesiani.
GEOMETRIA EUCLIDEA PIANA
TRIANGOLO
CLASSIFICAZIONE
LATI
Equilatero
Isoscele
Scaleno
ANGOLI
Acutangolo
Rettangolo
Ottusangolo
ESISTENZA
• Un triangolo esiste se ogni lato è minore della somma degli altri due
• Un triangolo esiste se ogni lato è maggiore della differenza degli altri due
PROPRIETA’
• Unendo i punti medi di due lati si ottiene un segmento parallelo alterzo lato e congruente
alla sua metà
• A lato maggiore sta opposto angolo maggiore e viceversa
• A lato minore sta opposto lato minore e viceversa
• E’ l'unico poligono a cui è sempre possibile circoscrivere e in cui è sempre possibile
inscrivere una circonferenza
• La somma degli angoli interni è uguale ad un angolo piatto, ossia 180°
• Ogni angolo esterno è uguale alla somma dei due angoli interni non adiacenti
PUNTI NOTEVOLI
 assi = circocentro
 mediane = baricentro
€
bisettrici = incentro
€
€
 altezze = ortocentro
TEOREMI
Dato un triangolo rettangolo valgono:
• TEOREMA di PITAGORA
€
• TEOREMA1 di EUCLIDE
i 2 = c12 + c 22
c12 = i ⋅ p1
h 2 = p1 ⋅ p2
• TEOREMA2 di EUCLIDE
dove i = ipotenusa c1 /c 2 = cateti p1 / p2 = proiezioni h = altezza relativa all’ipotenusa
€
€
€
€
€
€
€
QUADRILATERI
E' possibile rappresentare graficamente la famiglia dei quadrilateri mediante la relazione di
inclusione ricordando che un parallelogramma e' anche un trapezio
Osserva che:
PARALLELOGRAMMI
Lati opposti paralleli
C.N
•
•
•
•
C.S
Lati opposti congruenti
Angoli opposti congruenti
Diagonali si intersecano punti medi
(Angoli adiacenti ogni lato supplementari)
RETTANGOLO ha gli angoli tutti congruenti
ROMBO ha i lati tutti congruenti
Da cui
QUADRATO ha lati e angoli tutti congruenti
TRAPEZI
Due lati paralleli = basi
CIRCONFERENZA e CERCHIO
Circonferenza è il luogo dei punti del piano che si trovano ad una distanza data, detta raggio della
circonferenza, da un punto fisso, detto centro della circonferenza.
PARTI DI UNA CIRCONFERENZA
Diametro è la massima distanza esistente fra due punti appartenenti alla stessa circonferenza e
misura il doppio del raggio
Corda (in arancio)
proprietà:
• due corde hanno la stessa lunghezza se e solo se sono equidistanti dal centro della
circonferenza,
• una retta perpendicolare ad una corda e passante per il suo punto medio, passa anche per il
centro della circonferenza,
• una corda passante per il centro della circonferenza è un diametro.
Arco (in verde)
Angoli al centro e angoli alla circonferenza
• Ogni angolo al centro e' doppio dell'angolo alla circonferenza che insiste sullo stesso arco
(insistere sullo stesso arco significa che il loro arco e' lo stesso )
• Esistono infiniti angoli alla circonferenza sottesi
dallo stesso arco
Per questo ogni triangolo inscritto in una semicirconferenza è
un triangolo rettangolo
Cerchio
E’la porzione di piano delimitata da una circonferenza,
PARTI UN CERCHIO
Settore circolare è la porzione di un cerchio racchiusa da due
raggi e da un arco di circonferenza
Segmento circolare ad una base e' la parte di cerchio compresa
fra una sua corda e la circonferenza
Segmento circolare a due basi e' la parte di cerchio compresa
fra la circonferenza e due sue corde parallele
Corona circolare è un insieme di punti del piano compresi tra due cerchi concentrici.
FORMULARIO
Rettangolo
Area = A = b ⋅ h
d = b2 + h 2
€
Quadrato
€
Area = A = l 2
l= A
d=l 2
l=
€
€
d 2
2
Parallelogramma
€
€
Area = A = b ⋅ h
Triangolo scaleno
€
b⋅ h
2
A = p( p − a)( p − b)( p − c ) formula di Erone, p=semiperimetro
Area = A =
Triangolo rettangolo
€
€
Area = A =
h=
€
€
a⋅ b
c
b⋅ c a⋅ h
=
2
2
Triangoli particolari
Rombo
Perimetro = 2 p = 4l
Area = A =
d1 ⋅ d2
2
d12 + d22
l=
4
€
€
Trapezio
€
Area = A =
(b1 + b2 ) ⋅ h
2
€
Circonferenza e cerchio
Circonferenza = C = 2πr ⇒ r =
Area = A = πr 2 ⇒ r =
€
Settore circolare
€
€
€
π ⋅ r ⋅ α°
Arco = l =
180°
π ⋅ r2 ⋅ α°
Area = A =
180°
A
π
C
2π
Poligono circoscritto a una circonferenza
Area = A = p ⋅ r ⇒ perimetro = 2 p =
2A
r
,
€
Triangolo inscritto in una circonferenza
Area = A =
a⋅ b⋅ c
4r
Relazioni tra i lati dei poligoni regolari e i raggi delle circonferenze inscritte e/o circoscritte
€
Triangolo equilatero
1
1
1 l
l
raggioinscritto = r = mediana = h = ⋅
3=
3
3
3
3 2
6
2
2
2 l
l
raggiocircoscritto = R = mediana = h = ⋅
3=
3
3
3
3 2
3
€
Quadrato
€
raggioinscritto = r =
1
2
raggiocircoscritto = R =
Esagono
€
d l 2
=
2
2
€
raggioinscritto = r = htriangolo =
raggiocircoscritto = R = l
€
€
l
3
2
GEOMETRIA EUCLIDEA SOLIDA
I poliedri regolari sono cinque solidi formati da poligoni regolari uguali tra loro:
poliedro
facce
TETRAEDRO
4 facce = triangoli equilateri
OTTAEDRO
8 facce = triangoli equilateri
ICOSAEDRO
20 facce = triangoli equilateri
ESAEDRO (CUBO) 6 facce = quadrati
DODECAEDRO
12 facce = pentagoni
FORMULARIO
Cubo
Sl = 4l 2
St = 6l 2
V = l3
Prisma
Diagonalecubo = D = l 3
€
€
€€
Sl = 2 p ⋅ h
St = Sl + 2Sbase
V = Sbase ⋅ h
diagonale = d = a 2 + b 2 + c 2
€
Piramide
€
€ €
2p⋅ a
= p⋅ a
2
St = Sl + Sbase
S ⋅h
V = base
3
Sl =
€
€ S = 2πr ⋅ h
l
Cilindro
2
S
=
2
π
r
⋅
h
+
2
π
r
= 2πr( h + r)
t
€
V = πr 2 ⋅ h
Cono
€
€
€
Sl = 2πr ⋅ h
€
St = πr ⋅ a + πr 2 = πr( a + r)
πr 2 ⋅ h
V=
3
€
Sfera
€
S = 4πr 2
€
€
V=
4 3
πr
3