NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE
ROBERTO GIAMBÒ
1. D EFINIZIONI E PRIME PROPRIET À
In queste note saranno presentate alcune proprietà principali delle funzioni convesse di
una variabile reale, partendo dalla loro definizione. La prima cosa da osservare è che la
convessità può essere definita senza far ricorso ad ipotesi di regolarità sulla funzione, come
ad esempio la derivabilità, anche se vedremo che la convessità implica di per sé un certo
grado di regolarità della funzione. Vedremo poi condizioni equivalenti alla convessità che
sussistono sotto ipotesi più forti di regolarità sulla funzione.
Definizione 1.1. Sia f : I ! R una funzione reale definita in un intervallo I ✓ R. Allora f
si dice convessa in I se, 8x1 , x2 2 I, x1 6= x2 ,
(1)
f ((1
t)x1 + tx2 ) (1
t)f (x1 ) + tf (x2 ),
8t 2 (0, 1).
Se la proprietà espressa dalla relazione (1) vale con il verso della disuguaglianza ” ”, la
funzione si dice concava1.
Osservazione 1.2. La proprietà (1) esprime la condizione geometrica che, comunque scelti
due punti distinti x1 , x2 2 I, i punti del grafico di f (x) tra x1 ed x2 non si trovano sopra il
segmento di retta secante il grafico stesso, di estremi (x1 , f (x1 )) e (x2 , f (x2 )).
Date: Versione del 18 settembre 2013.
1
Nel resto di queste note, ci occuperemo solo delle funzioni convesse. Osservando che f è concava se e solo
se f è convessa, risultati e considerazioni analoghi a quelli che vedremo valgono, con opportune modifiche,
anche per le funzioni concave.
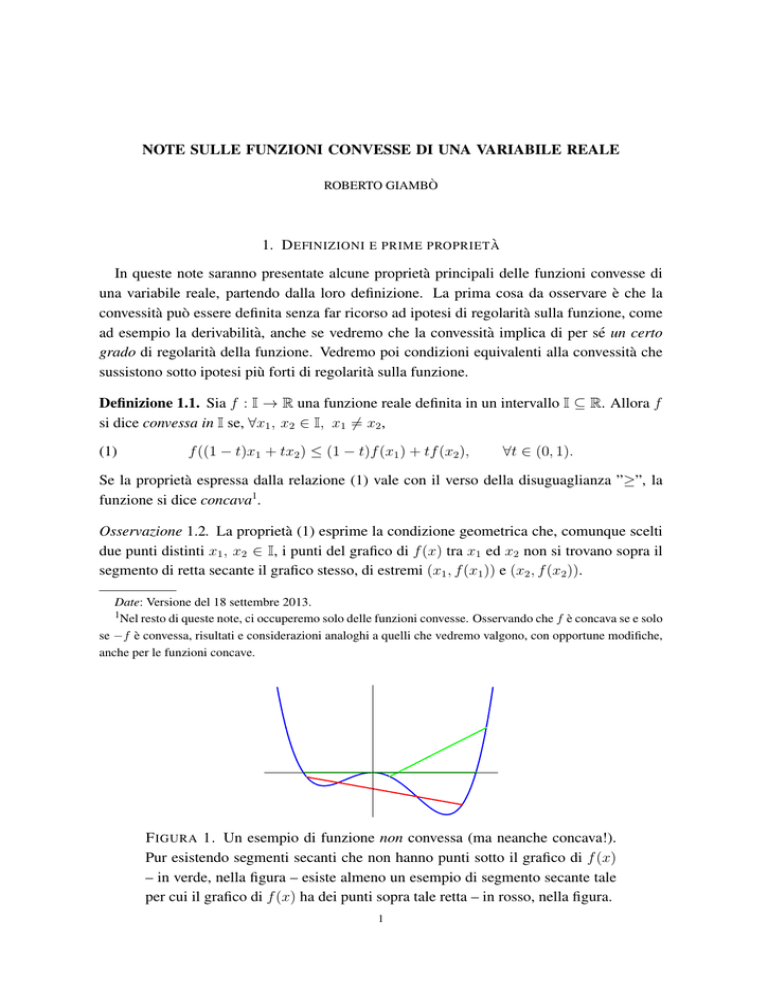
F IGURA 1. Un esempio di funzione non convessa (ma neanche concava!).
Pur esistendo segmenti secanti che non hanno punti sotto il grafico di f (x)
– in verde, nella figura – esiste almeno un esempio di segmento secante tale
per cui il grafico di f (x) ha dei punti sopra tale retta – in rosso, nella figura.
1
2
R. GIAMBÒ
F IGURA 2. Gli esempi dell’Osservazione 1.3. Una funzione convessa non
è necessariamente derivabile ovunque (vedi esempio a sinistra), e nemmeno
ovunque continua (vedi esempio a destra).
Quindi, è immediato constatare che la condizione di convessità si esprime equivalentemente come segue:
(2)
f (x) f (x1 ) +
f (x2 )
x2
f (x1 )
(x
x1
x1 ),
8x1 , x2 2 I, x1 < x2 , 8x 2 (x1 , x2 ).
Osservazione 1.3. Una funzione convessa non è necessariamente derivabile in tutto il dominio: si consideri ad esempio f (x) = |x| (vedi Figura 2). Inoltre, se l’intervallo di definizione contiene punti di frontiera, la funzione può anche non essere continua in tali punti: si
consideri ad esempio la funzione g(x) : [0, 1] ! R,
8
<1, x 2 {0, 1},
g(x) =
:0, x 2 (0, 1).
Vedremo però tra poco che la convessità implica almeno la continuità nei punti interni del
dominio (Corollario 1.5).
Preso x1 < x2 , osserviamo che la condizione (2) è equivalente alla seguente
(3)
f (x)
x
f (x1 )
f (x2 )
x1
x2
f (x1 )
,
x1
8x, x1 , x2 2 I, x1 < x < x2
f (x2 )
,
x2
8x, x1 , x2 2 I, x1 < x < x2 .
oppure, permutando x1 e x2 nella (2),
(4)
f (x)
x
f (x2 )
x2
f (x1 )
x1
Per l’arbitrarietà dei punti scelti, la condizione (3) esprime la proprietà che, fissato x0 ,
l’applicazione
f (x) f (x0 )
x 7!
x x0
che manda x nel rapporto incrementale di f in x0 , calcolato in x, è crescente a destra di x0
(cioè per x > x0 ). Analogamente, la condizione (4) esprime la proprietà che la medesima
applicazione è crescente a sinistra di x0 . Ricordando che le funzioni monotone ammettono
sempre limiti laterali, questo significa che i limiti laterali del rapporto incrementale di una
funzione convessa esistono sempre.
FUNZIONI CONVESSE
3
Inoltre, usando di nuovo la (2), si ha, per x 2 (x1 , x2 ),
(x2 x1 )f (x) (x2 x1 )f (x1 )+(f (x2 ) f (x1 ))(x x1 ) = (x2 x)f (x1 )+(x x1 )f (x2 )
) (x2
x1 )f (x) (x2
x)f (x) + (x
) (x2
x)(f (x)
x)f (x1 ) + (x
f (x1 )) (x
x1 )f (x2 )
x1 )(f (x2 )
f (x)),
da cui la proprietà (sostituendo x con x0 )
(5)
f (x1 )
x1
f (x0 )
f (x2 )
x0
x2
f (x0 )
,
x0
8x0 , x1 , x2 2 I, x1 < x0 < x2
che esprime la proprietà che l’applicazione rapporto incrementale di f in x0 assume a sinistra
di x0 valori non superiori di quelli che assume a destra. Quindi, se il punto x0 è interno
all’intervallo I di definizione della funzione, il limite destro del rapporto incrementale di f
in x0 (che esiste, per quanto detto poco fa) è limitato dal basso da un qualunque valore del
rapporto incrementale per x < x0 , e dunque è finito. Analogamente, il limite sinistro del
rapporto incrementale di f in x0 è limitato dall’alto da un qualunque valore del rapporto
incrementale per x > x0 , e dunque è finito anch’esso. La seguente proposizione riassume
quanto appena dimostrato.
Proposizione 1.4. Sia f : I ! R convessa. Allora, se x0 è un punto interno ad I, esistono la
derivata destra e sinistra di f in x0 , e si ha f+0 (x0 ) f 0 (x0 ). Se x0 è un punto di frontiera
per I, il limite del rapporto incrementale per x ! x0 esiste sempre, ma può non essere
finito.
Dalla proposizione 1.4 discende immediatamente il seguente
Corollario 1.5. Una funzione convessa f : I ! R è continua nei punti interni ad I.
Dimostrazione. Si usa un argomento analogo a quello necessario per provare che una funzione derivabile è continua. Sia x0 un punto interno ad I: esistendo allora le derivate laterali
di f 0 in x0 possiamo dire che, ad esempio,
lim+
x!x0
f (x)
x
f (x0 )
= f+0 (x0 ) 2 R
x0
e quindi
(6)
f (x)
f (x0 ) = f+0 (x0 )(x
x0 ) + q(x)(x
x0 ),
con limx!x+0 q(x) = 0. Passando al limite per x ! x+
f (x) =
0 nella (6) si ottiene limx!x+
0
f (x0 ). Analogamente si ragiona a sinistra di x0 .
⇤
Osservazione 1.6. Si noti che la Proposizione 1.4 non ci dice che f è derivabile nei punti
interni di I: le derivate laterali, infatti, possono non coincidere (si ripensi nuovamente all’esempio f (x) = |x|, per x0 = 0). Tuttavia, è possibile dimostrare il seguente risultato:
se f : I ! R è convessa, allora l’insieme dei punti in cui f non è derivabile è al più
numerabile. La dimostrazione di questo fatto si trova in appendice a queste note.
4
R. GIAMBÒ
Esercizio 1.7. Se f : I ! R è una funzione convessa (non necessariamente derivabile su
tutto I) che ammette un minimo relativo, allora si provi che esso è anche il minimo assoluto
di f .
2. C ONVESSIT À E DERIVABILIT À
Supponiamo ora che f una funzione reale definita in un intervallo aperto (a, b) ✓ R (non
necessariamente limitato), e che f (x) sia derivabile in tutti i punti di (a, b). Allora è possibile
caratterizzare la proprietà di convessità di f in (a, b) in due modi diversi. Vediamoli.
Teorema 2.1. Sia f (x) : (a, b) ! R derivabile. Allora, le seguenti tre proprietà sono
equivalenti:
(a) f (x) è convessa in (a, b);
(b) f 0 (x) è crescente in (a, b);
(c) f (x) f (x0 ) + f 0 (x0 )(x x0 ), 8x, x0 2 (a, b).
Dimostrazione. Dimostreremo che (a) , (c) e che (b) , (c). Si noti che la (c) esprime la
nota condizione che il grafico di f (x) non si trova mai al di sotto della tangente al grafico
stesso in un qualunque suo punto.
(a) ) (c):
Dalla condizione (3) si ottiene, passando al limite nel primo membro per x ! x+
1 , che
0
f (x1 )(x2 x1 ) f (x2 ) f (x1 ) se x1 < x2 per cui, rinominando x1 e x2 come x0 e
x rispettivamente, si ottiene la (c) nel caso x0 < x. Dalla (4) si ottiene invece, passando
sempre nel primo membro al limite per x ! x2 , che f 0 (x2 )(x2 x1 ) f (x2 ) f (x1 ) se
x1 < x2 , da cui, rinominando x1 e x2 come x e x0 rispettivamente, si ottiene la condizione
(c) per x < x0 .
(c) ) (a):
Sia x1 < x2 , e x0 2 (x1 , x2 ). Sia t(x) la retta tangente al grafico di f in x0 (quindi
t(x) = f (x0 ) + f 0 (x0 )(x x0 )) e sia s(x) la secante da x1 a x2 (per cui s(x) = f (x1 ) +
f (x2 ) f (x1 )
(x x1 )). Allora s(x1 ) = f (x1 ) per costruzione, e f (x1 ) t(x1 ) per l’ipotesi (c),
x2 x1
da cui s(x1 ) t(x1 ). Analogamente s(x2 ) t(x2 ). Ma s(x) e t(x) sono rette, dunque se
s t in x1 e in x2 , dovrà essere s(x) t(x), 8x 2 [x1 , x2 ] e dunque anche s(x0 ) t(x0 ).
Ma t(x0 ) = f (x0 ) per costruzione, dunque abbiamo provato che s(x0 ) f (x0 ), cioè che in
x0 il grafico della f non sta sopra la retta secante. Per l’arbitrarietà di x0 , tale proprietà vale
per qualunque x0 2 (x1 , x2 ), comunque scelti i punti x1 < x2 , per cui la f è convessa.
(b) ) (c):
Sia x > x0 . Dal teorema di Lagrange 9⇠ 2 (x0 , x) tale che f (x)x fx0(x0 ) = f 0 (⇠) f 0 (x0 ),
dove nell’ultima disuguaglianza si sfrutta l’ipotesi (b), ottenendo la (c) quando x > x0 . Si
ragiona analogamente quando x < x0 .
(c) ) (b):
Dall’ipotesi si ottiene, considerando due punti x1 e x2 :
FUNZIONI CONVESSE
5
f (x1 )
f (x2 ) + f 0 (x2 )(x1
x2 )
f (x2 )
f (x1 ) + f 0 (x1 )(x2
x1 ).
Sommando membro a membro e semplificando si ha
(f 0 (x2 )
f 0 (x1 ))(x1
x2 ) 0,
⇤
da cui il fatto che, quando x1 < x2 , f 0 (x1 ) f 0 (x2 ).
Esercizio 2.2. Sia f : (a, b) ! R una funzione convessa e derivabile, e sia x0 un punto
critico per f . Si provi che x0 è un punto di minimo globale.
Come corollario del Teorema 2.1 si ottiene una ben nota caratterizzazione delle funzioni
convesse nel caso in cui esse siano derivabili due volte.
Corollario 2.3. Sia f : (a, b) ! R derivabile due volte. Allora f è convessa in (a, b) se e
solo se f 00 (x) 0, 8x 2 (a, b).
Dimostrazione. Per ipotesi f è derivabile quindi, dal Teorema 2.1, f è convessa se e solo
se f 0 (x) è crescente. D’altra parte, essendo f 0 (x) derivabile una volta per ipotesi, il criterio
di monotonia per funzioni derivabili ci dice che f 0 (x) è crescente se e solo se (f 0 )0 (x) 0,
cioè se e solo se f 00 (x) 0.
⇤
3. C ONVESSIT À STRETTA
Iniziamo con il definire il concetto di convessità stretta. Una funzione qualunque f : I !
R definita in un intervallo I ✓ R, è detta strettamente convessa in I se la disuguaglianza (1)
è stretta, indipendentemente dalla scelta dei due punti distinti x1 , x2 2 I. Analogamente si
definiscono le funzioni strettamente concave.
Osservazione 3.1. Se f : (a, b) ! R è derivabile allora la convessità stretta è equivalente a
dire che f 0 (x) è strettamente crescente in (a, b), ed entrambe le condizioni sono equivalenti
a dire che
(7)
f (x) > f (x0 ) + f 0 (x0 )(x
x0 ),
8x, x0 2 (a, b), x 6= x0 .
L’argomento da usare per provare l’equivalenza di queste tre proprietà è lo stesso di quello
usato nel Teorema 2.1, con opportune modifiche. Si noti in particolare che, per provare l’analogo di (a))(c), occorre prima enunciare l’analogo della (3) nel caso di stretta convessità,
che è
f (x) f (x1 )
f (x2 ) f (x1 )
(8)
<
, 8x, x1 , x2 2 I, x1 < x < x2
x x1
x2 x1
ed osservare che, nel passaggio al limite per x ! x+
1 , si ha
(9)
f (x)
x
f (x1 )
x1
inf
x>x1
f (x)
x
f (x1 )
f (x)
= lim
x!x1
x1
x
f (x1 )
= f+0 (x1 ),
x1
6
R. GIAMBÒ
dove la prima uguaglianza nella (9) dipende dal fatto che il rapporto incrementale è una
funzione monotona (vedi Proposizione 1.4). Perciò, usando (8) e (9) si ottiene la condizione
con la disuguaglianza stretta, cioè la (7) nel caso x > x0 . Analogamente si ragiona nel caso
x < x0 , usando l’analogo della (4) nel caso di stretta convessità. Il resto dell’argomento può
essere ripetuto come nel Teorema 2.1, usando le disuguaglianze strette in luogo di quelle
larghe.
Esercizio 3.2. Sia f : (a, b) ! R è strettamente convessa e derivabile. Si provi che f
ammette al più un punto critico. Usare l’esercizio 2.2 per provare che se questo punto esiste,
esso è (l’unico) punto di minimo assoluto per f .
Osservazione 3.3. Sia f : (a, b) ! R derivabile due volte. Se la derivata seconda è strettamente positiva, f 00 (x) > 0, allora f 0 è strettamente crescente e quindi f è strettamente
convessa (vedi Osservazione 3.1). Ma questa è solo una condizione sufficiente, non necessaria, per avere f strettamente convessa: si prenda ad esempio f (x) = x4 che è due volte
derivabile e strettamente convessa, ma la cui derivata seconda si annulla per x = 0. Usando
però il criterio di monotonia stretta di una funzione, se f : (a, b) ! R è due volte derivabile,
si può provare che la convessità stretta equivale alla condizione seguente: f 00 (x) 0 in (a, b)
e non esiste alcun intervallo contenuto in (a, b) nel quale f 00 (x) si annulla identicamente.
A PPENDICE A. D ERIVABILIT À DI FUNZIONI CONVESSE
In questa sezione dimostreremo il Teorema enunciato nell’Osservazione 1.6.
Teorema A.1. Se f : I ! R è convessa, allora l’insieme dei punti in cui f non è derivabile
è al più numerabile.
Dimostrazione. Anzitutto, senza perdità di generalità si può supporre che I sia un intervallo
aperto. Sia allora g(x) = f+0 (x) f 0 (x) l’applicazione che associa ad un punto la differenza
tra le derivate laterali calcolate in quel punto (le quali esistono grazie alla Proposizione 1.4),
differenza che per la convessità di f è non negativa. Si proverà che l’insieme
A = {x 2 I : g(x) > 0}
è al più numerabile. Dividiamo la dimostrazione in passi.
(1) Fissato un qualunque intervallo chiuso e limitato [a, b] ⇢ I, e un qualunque n 2 N
positivo, allora l’insieme
⇢
1
n
Aa,b = x 2 [a, b] : g(x) >
n
contiene un numero finito di punti.
Infatti, fissati [a, b] ed n, supponiamo per assurdo che esista una successione infinita xj 2 Ana,b , e ordiniamo gli xj in modo tale che la successione sia strettamente
crescente. Detto k un numero intero tale che
(10)
k > n(f 0 (b)
f+0 (a)),
FUNZIONI CONVESSE
7
consideriamo l’insieme di punti
{xj }j=1,...,k .
Allora, la convessità implica che
f+0 (a) f 0 (x1 ) f+0 (x1 ) f 0 (x2 ) f+0 (x2 ) . . . f 0 (xk ) f+0 (xk ) f 0 (b),
e quindi da ciò segue che
(11)
0
f (b)
f+0 (a)
k
X
(f+0 (xk )
0
f (xk )) =
j=1
k
X
g(xj ) > k/ n,
j=1
dove nell’ultima disuguaglianza si è sfruttato il fatto che g(xj ) > 1/n. Dal confronto
tra (10) e (11) si ottiene una contraddizione.
(2) Fissato un qualunque intervallo chiuso e limitato [a, b] 2 I, l’insieme
Aa,b = {x 2 [a, b] : g(x) > 0}
è al più numerabile.
Infatti si osserva subito che
Aa,b =
1
[
Ana,b
n=1
e dunque è unione numerabile di insiemi finiti, per cui è al più numerabile.
A questo punto siamo in grado di provare l’ultimo passo, e cioè
(3) l’insieme A = {x 2 I : g(x) > 0} è al più numerabile.
Basta osservare che un qualunque intervallo aperto I può essere visto come unione
numerabile di intervalli chiusi e limitati (ad esempio, se I = (a, b), allora I =
1
1
[1
]). Poiché su ciascuno di questi intervalli chiusi l’insieme dei punti
n=1 [a + n , b
n
tali che f non è derivabile è al più numerabile, allora anche A, che è l’unione di tutti
questi insiemi di punti in cui f non è derivabile, sarà al più numerabile.
⇤
Esercizio A.2. Sfruttando un argomento simile a quello usato nella dimostrazione del Teorema A.1, mostrare che, data una funzione monotona f : I ! R, l’insieme dei punti in cui
f non è continua è al più numerabile.












