Cine%ca enzima%ca Copyright © 2013 Zanichelli editore S.p.A.
La cinetica delle reazioni
Conce, chiave • Le semplici equazioni di velocità descrivono il progredire delle reazioni di primo e di secondo ordine. • L'equazione di Michaelis-­‐Menten me<e in relazione la velocità iniziale di una reazione con la velocità massima e con la costante di Michaelis per un par=colare enzima e un dato substrato. • L'efficienza catali=ca complessiva di un enzima è espressa come kcat/KM. • Il grafico di Lineweaver-­‐Burk può essere u=lizzato per presentare i da= cine=ci e per calcolare i valori di KM e Vmax. Richiami di Cine=ca Chimica La cine=ca chimica studia la velocità e il meccanismo con cui procede una reazione chimica. La velocità di reazione è la velocita di trasformazione di questo o quel reagente o la velocità di formazione di questo o quel prodo<o. Reazioni elementari e molecolarità di reazione La maggior parte delle reazioni si prestano ad essere analizzate in una successione di fasi (reazioni elementari, o even= reaNvi) a ciascuna delle quali partecipano, una, due, o, molto più raramente, tre molecole. La molecolarità di un singolo evento reaNvo è il numero di molecole che vi prendono parte. Un evento monomolecolare vede la scissione di una sola molecola o il riordinarsi dei suoi atomi in una nuova disposizione. Se l’evento è bimolecolare, saranno due molecole ad urtarsi, scambiandosi energia, atomi, gruppi di atomi o subendo qualche altgro =po di trasformazione. Il meccanismo cine=co di una reazione è la sequenza di reazioni elementari che vi prendono parte. Meccanismo di reazione Data una determinata reazione chimica: Il meccanismo cine=co con cui procede è la sequenza di reazioni elementari che dai reagen= portano ai prodoN. Per es., Prima reazione elementare, monomolecolare Seconda reazione elementare, bimolecolare
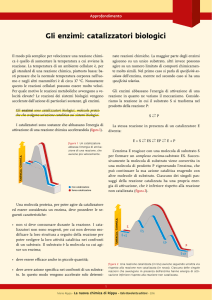
Equazione cine=ca di reazione La dipendenza funzionale della velocità di una reazione dalle concentrazioni delle specie reagen= è espressa dall’equazione cine=ca: La cui forma esplicita può essere di vario =po e deve essere caso per caso determinata sperimentalmente. Almeno nelle fasi iniziali, quando i prodoN non si sono ancora sufficientemente accumula=, la velocità della reazione risulta dire<amente proporzionale al prodo<o delle concentrazioni dei reagen= elevate ad opportuni esponen=, interi o frazionari (e talora anche nega=vi): Costante cine=ca e ordine di reazione La costante di proporzionalità dell’equazione cine=ca è funzione della temperatura ed è chiamata costante cine%ca (è numericamente uguale alla velocità di reazione quando tu<e le concentrazioni dei componen= sono unitarie). Si definisce ordine totale della reazione la somma degli esponen= a cui sono elevate le concentrazioni dei componen=; mentre i singoli esponen= rappresentano gli ordini parziali della reazione rispe<o a ciascun componente. Né l’equazione cine=ca, né gli ordini parziali di ciascuna specie partecipante alla reazione sono deducibili dall’equazione stechiometrica. InfaN, la forma dell’equazione cine=ca e l’ordine della reazione rispe<o a ciascun componente dipendono dal meccanismo con cui la reazione si svolge. Equazioni cine=che e reazioni elementari Equazione di Arrhenius CINETICA ENZIMATICA La cine%ca enzima%ca è lo studio delle velocità di reazione catalizzate da enzimi. Il suo studio consente di individuare il meccanismo di catalisi. Meccanismo cine+co In condizioni di velocità iniziale, [P] ~ 0, quindi possiamo trascurare la reazione che dai prodoN porta ad ES: Curva di progressione di una semplice reazione catalizzata da un enzima Stato stazionario Velocità iniziale Condizioni per lo studio della cine%ca enzima%ca [S]0 >> [E]0 dt tale che Δ[S] ~ 0 e [P] ~ 0 in pra=ca: Δ[S] < 10% Meccanismo cine%co di Michaelis Menten Secondo questo meccanismo semplificato, l'enzima libero (E) interagisce con il substrato (S), dando origine al complesso enzima-­‐substrato (ES, deUo anche complesso di Michaelis Menten), il quale si scomporrà originando il prodoUo della reazione enzima%ca (P) e riformando l'enzima libero Riassumendo schema%camente: dove i termini indica% con k rappresentano le costan% cine%che rela%ve alle diverse tappe elementari del meccanismo cine%co. In condizioni di velocità iniziale si ha che [P] ~ 0, quindi si può trascurare la tappa di reazione che dai prodoN porta a ES: Secondo questo meccanismo la tappa che limita l’intera reazione è la scomposizione del complesso ES nel prodoUo e nell’enzima libero, cioè la tappa reUa dalla costante cine%ca k2, deUa anche costante catali%ca. stadio lento
A questo punto si considera la condizione dello stato stazionario. In tale stato, la [ES] è costante, non perché il sistema abbia raggiunto l’equilibrio, ma perché la velocità di formazione di ES è esa<amente bilanciata dalla sua velocità di scomparsa. L’unica tappa implicata nella formazione di ES è re<a dalla costante cine=ca k1; le reazioni elementari che portano alla scomparsa di ES sono quelle re<e dalle costan= cine=che k-­‐1 e k2: Dopo lo stato prestazionario, la [ES] rimarrà costante in quanto: Riarrangiando: (per la conservazione della massa) (qui [S] coincide pra=camente con [S]0, in quanto si è nelle condizioni iniziali di reazione e, inoltre, [E]T è trascurabile rispe<o a [S]0) Si no% che visto che k2 e [E]0 sono costan%, il loro prodoUo è una costante e corrisponde alla velocità massima, Vmax. L'equazione di Michaelis-­‐Menten può anche essere espressa nella forma alterna%va (più usata): L'equazione di Michaelis-­‐Menten me<e, quindi, in relazione la velocità di formazione (iniziale) del prodo<o V0 con la concentrazione del substrato [S]. La curva di Michaelis-­‐Menten, un’iperbole re<angolare, descrive l'andamento della velocità di una reazione catalizzata da enzimi, al variare della concentrazione del substrato. Questa equazione è generalmente valida per gli enzimi non allosterici. Il modello cine=co di Michaelis Menten spiega come all'aumentare della concentrazione del substrato disponibile per una data quan=tà di enzima, la velocità della reazione aumen= in modo lineare con la [S] quando questa sia trascurabile rispe<o al valore Km. In corrispondenza di tale valore la reazione raggiunge il suo valore semimassimale (i.e., 1/2 Vmax). A [S] più elevate, la velocità della reazione tende a aumentare in modo non-­‐lineare e via via sempre più lentamente fino al raggiungimento di un valore massimo, chiamato velocità massima (Vmax). In questo punto è presente tanto substrato da saturare tu<o l'enzima presente in soluzione, perciò un'ulteriore aggiunta di substrato non servirebbe, in quanto non verrebbe più a<accato da enzimi, che sono tuN già lega= al substrato. KM
La costante di Michaelis-­‐Menten, KM, rappresenta la concentrazione di substrato necessaria, affinché la reazione abbia velocità pari a metà della velocità massima Essa equivale al seguente rapporto tra costan% di velocità: La costante di Michaelis-­‐Menten è una grandezza caraUeris%ca di ciascun enzima. Essa indica quan%ta%vamente l'affinità tra un enzima e il suo substrato: più basso è il valore di KM e più bassa sarà la concentrazione di substrato che permeUe di raggiungere un valore di velocità di reazione pari alla metà della velocità massima, il che indica un’alta affinità dell'enzima per il substrato. Viceversa, un alto valore di KM indica che sarà necessario più substrato per raggiungere una velocità di reazione pari alla metà della velocità massima, il che significa una minore affinità dell'enzima per il substrato. La cinetica di Michaelis-Menten
La costante di Michaelis-Menten: KM
La costante KM viene spesso associata all’affinità dell’enzima per il substrato. Questa relazione è matema%camente vera solo nel caso del meccanismo di Michaelis Menten, in cui si abbia che k2 << k-­‐1 e quindi si o,ene: k1
k2
Trascurabile rispe<o a k-­‐1 E+S
k-1
ES
E+P
KS = k-­‐1/k1 ≅ KM Dove KS è la costante di equilibrio (di dissociazione) definita dalla seguente equazione: KS = k-­‐1/k1 = [E][S]/[ES] Quindi, quando la velocità di formazione del prodoUo è molto bassa, la KM è una misura dell’inverso della forza di legame del substrato all’enzima. Costante Catalitica/Numero di
Turnover
Efficienza catali%ca: kcat/KM Quando [S]<<KM la maggior parte delle molecole di enzima è in forma libera e l’eq. di M.M. prende la forma: Limite fisico al valore di kcat/KM k2k1 < k2k1 + k-­‐1k1 ... kcat/KM<k1 Velocità di Diffusione: 108-­‐109 M-­‐1s-­‐1 I parametri della cinetica enzimatica
Velocità di Diffusione: 108-­‐109 M-­‐1s-­‐1 Perfezione catali=ca Grafico dei doppi reciproci
(di Lineweaver-Burk)
La cinetica delle reazioni
Punto di verifica • Scrivete le equazioni di velocità per una reazione di
primo ordine e per una di secondo ordine.
• Che differenze vi sono tra la velocità istantanea, la
velocità iniziale e la velocità massima di una reazione
enzimatica?
• Ricavate l'equazione di Michaelis–Menten.
La cinetica delle reazioni
Punto di verifica • Cosa rivelano i valori di KM e di kcat/KM riguardo a un
enzima? • Perché un enzima non può avere un valore del
rapporto kcat/KM più grande di 109 M–1 ·∙ s–1? • Scrivete l'equazione di Lineweaver-Burk (dei doppi
reciproci) e descrivete le caratteristiche di un grafico di
Lineweaver-Burk.