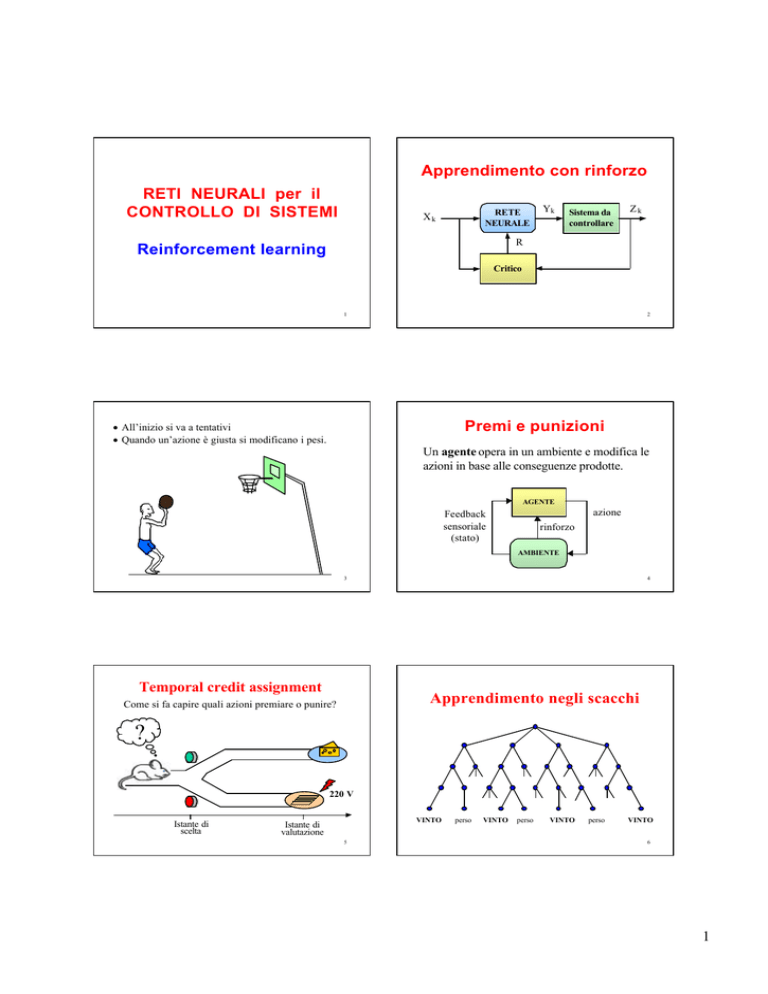
Apprendimento con rinforzo
RETI NEURALI per il
CONTROLLO DI SISTEMI
RETE
NEURALE
Xk
Yk
Sistema da
controllare
Zk
R
Reinforcement learning
Critico
1
2
Premi e punizioni
• All’inizio si va a tentativi
• Quando un’azione è giusta si modificano i pesi.
Un agente opera in un ambiente e modifica le
azioni in base alle conseguenze prodotte.
AGENTE
•
azione
Feedback
sensoriale
(stato)
rinforzo
AMBIENTE
3
Temporal credit assignment
4
Apprendimento negli scacchi
Come si fa capire quali azioni premiare o punire?
?
220 V
Istante di
scelta
VINTO
Istante di
valutazione
5
perso
VINTO
perso
VINTO
perso
VINTO
6
1
Modello a scatole
Modello a scatole (Michie/Chamber ‘68)
• Apprendimanto basato su punizioni.
BOX 1
Local demon A1
• Si quantizza lo spazio degli stati in N
regioni disgiunte (box).
Global
demon
A2
••
•
An
•
•
• Ogni volta che il sistema entra in uno stato
(box) viene scelta un'azione di controllo.
BOX m
SISTEMA
•
••
Local demon A1
220 V
A2
••
•
An
•
• Il controllore deve imparare a fare l'azione
che più ritarda la punizione.
critico
7
Modello neurale: ASE-ACE
Adaptive Search Element
(Barto-Sutton-Anderson, ‘83)
ASE: Associative Search Element
ACE: Adaptive Critic Element
ACE
8
r
r
x1
x2
Sistema in stato xi
xi = 1
xj = 0 ∀ j ≠ i
ASE
xn
r*
x1
stato
DECODER
xm
y
•
•
•
y
ASE
n
y( t) = sgn∑ wi xi + n (t)
i =1
SISTEMA
•
•
•
n(t) è una variabile gaussiana con
valor medio nullo e varianza σ2
9
Adaptive Search Element
Adaptive Search Element
I pesi dell’ASE sono aggiornati con la seguente legge:
n
y( t) = sgn∑ w i xi + n( t)
i =1
L’ASE può generare solo due azioni:
10
∆wi(t) = α r(t) ei(t)
a ++ (y = 1)
a −− (y = 0)
α
è una costante positiva ( learning rate)
r(t)
è il segnale di rinforzo
Quando il sistema è nello stato x i (xi = 1) si ha che:
r(t) =
• se wi = 0,
le
• se wi > 0,
a++ è scelta con maggiore probabilità
• se wi < 0,
a−− è scelta con maggiore probabilità
azioni a ++ e
a−− sono equiprobabili
11
ei(t)
−1
0
in caso di fallimento
altrimenti
è un segnale ( elegibilità) che introduce una
memoria a breve termine sulle sinapsi:
ei(t+1) = δ ei(t) + (1 − δ) y(t) x i (t)
12
2
Adaptive Search Element
Adaptive Search Element
∆wi(t) = α r(t) ei(t)
∆wi(t) = α r(t) ei(t)
ei(t+1) = δ ei(t) + (1 − δ) y(t) x i (t)
ei(t+1) = δ ei(t) + (1 − δ) y(t) x i (t)
Un fallimento (r < 0) riduce la probabilità di
scelta delle azioni recenti che lo hanno causato:
Un successo (r > 0) aumenta la probabilità di
scelta delle azioni recenti che lo hanno causato:
a ++ ⇒ ei(t) > 0 ⇒ ∆wi < 0
a ++ ⇒ ei(t) > 0 ⇒ ∆wi > 0
a −− ⇒ ei(t) < 0 ⇒ ∆wi > 0
a −− ⇒ ei(t) < 0 ⇒ ∆wi < 0
13
14
Elegibilità
Importanza dell’ACE
ei(t+1) = δ ei(t) + (1 − δ) y(t) x i (t)
• Man mano che i fallimenti si riducono, il sistema
tenderebbe ad imparare più lentamente.
∆wi(t) = α r(t) ei(t)
e 1(t)
x1
∆w1 = −α E1
• Allora si introduce un critico adattivo (ACE), che
genera un rinforzo secondario più informativo.
∆w2 = −α E2
• Osservando lo stato del sistema e i fallimenti,
l’ACE impara a prevedere gli stati pericolosi.
x2
e 2(t)
t1 t2
a+ a−−
t3
a+
• Esso genera un premio (r* > 0) se il sistema si
allontana da uno stato pericoloso; una punizione
(r* < 0 ) in caso contrario.
∆wn = −α En
e n(t)
xn
t4
FAIL
15
16
Adaptive Critic Element
x1
x2
p
ACE
xn
•
•
•
γp(t) − p(t-1)
Adaptive Critic Element
r
rinforzo
primario
+
x1
x2
p
ACE
r*
rinforzo
secondario
• L’ACE è addestrato in modo che p(t) converga
verso una previsione del rinforzo primario.
• Quindi, r* viene generato in funzione della
variazione della previsione.
17
xn
•
•
•
γp(t) − p(t-1)
r
rinforzo
primario
+
rinforzo
r* secondario
p =
n
∑ v i xi
i= 1
∆vi (t) = β [r(t) + p(t) − p(t−1)] τi(t)
τi(t+1) = λ τi (t) + (1 − λ) x i (t)
18
3
Rinforzo secondario
Rinforzo secondario
r *(t) = r(t) + γp(t) − p(t−1)
r *(t) = r(t) + γp(t) − p(t−1)
• Se (r = 0) incrementi della previsione si traducono
in premi (r* > 0 ), decrementi in punizioni (r* < 0).
• Se (r = −1),
−1 x i = 0 ∀i, quindi p(t) = 0. Dunque:
– Se il fallimento è stato predetto [p(t−1) = r(t)] si
ha r* = 0, tuttavia le azioni recenti sono state già
punite negli istanti precedenti.
p(t)
t
– Se il fallimento non è stato predetto [p(t−1) = 0]
si ha r* < 0, che comunque genera punizione.
-1
punizione
premio
punizione
19
20
Possibili Applicazioni
•
Pendolo inverso
Studiare l’apprendimento di semplici organismi.
θ
Es: formiche, vermi, topi ...
•
Controllo adattivo di sistemi di cui non sono note
le caratteristiche:
F
Es: pendoli inversi, guida automatica di veicoli
x
21
22
Guida automatica
Tendenze della ricerca
•
•
•
23
Sviluppare circuiti neurali hardware
velocizzare la risposta di reti molto grosse.
per
Studiare meccanismi di apprendimento più robusti
ed efficienti, per il controllo di robot autonomi.
Utilizzare le reti neurali per effettuare previsioni
di eventi sulla base della storia passata.
24
4












