La continuità di una funzione

La continuità di una funzione
Introduzione
L'argomento legato ai limiti di una funzione porta in modo diretto al concetto di continuità e,
conseguentemente, allo studio delle discontinuità di una funzione. La tematica si esaurisce, poi,
nella teoria del concetto di andamento asintotico con conseguente calcolo delgi asintoti della
funzione stessa.
Tali aspetti sono rilevanti ai fini della rappresentazione del tracciato grafico di una funzione, poichè
riescono a definire se, ed in che modo, puntare l'attenzione su particolari valori della variabile X, in
cui il tracciato grafico potrebbe interrompere la sua continuità.
A livello intuitivo il concetto di contuinuità non presenta particolari difficoltà nella sua comprensione,
essendo legato alla "continuità" del tratto con cui se ne disegna il grafico.
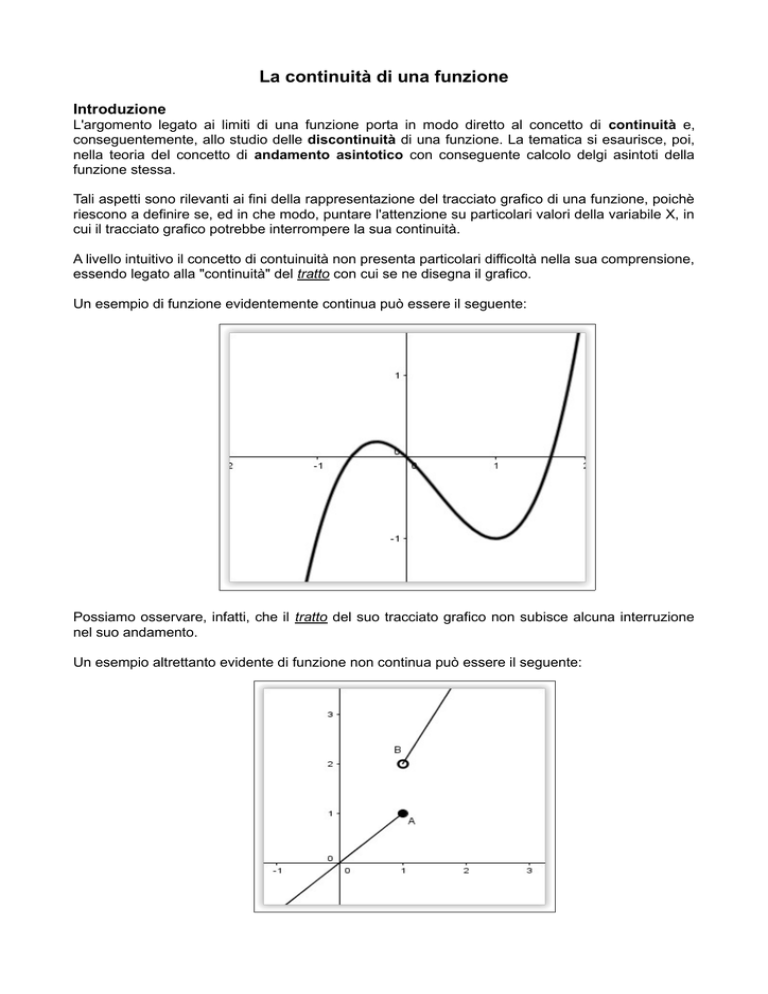
Un esempio di funzione evidentemente continua può essere il seguente:
Possiamo osservare, infatti, che il tratto del suo tracciato grafico non subisce alcuna interruzione
nel suo andamento.
Un esempio altrettanto evidente di funzione non continua può essere il seguente:
In questo caso il tracciato grafico della funzione subisce un'interruzione in prossimità di X = 1.
Ciò che questo capitolo si propone è di fornire adeguati strumenti per studiare rigorosamente la
continuità di una funzione, ed analizzare la tipologia di eventuali punti di discontinuità.
Funzioni continue
Vediamo ora come riuscire a stabilire se una funzione è continua, partendo dall'osservazione che è
possibile definire due tipi di continuità:
Continuità in un punto
Una funzione Y = f(x) si dice continua in un punto X = a se è verificata la seguente uguaglianza
lim f ( x)
lim f ( x)
=
=
−.
x →a
x → a +.
f (a )
In base all'uguaglianza possiamo osservare che una funzione risulta continua in un punto solo se il
suo andamento non subisce "interruzioni" in un intorno del punto considerato.
Esempio
Verificare che la funzione
f (x )=
x+2
è continua nel punto di ascissa x = 1
x
Applicando la definizione di continuità in un punto andiamo a verificare che i limiti sinistro e destro
per x che tende a 1 coincidono, ed il loro valore è uguale a f(1).
Per iniziare calcoliamo f(1)
f (1)=
1+2
=3
1
Andiamo adesso a calcolare il limite per difetto ed il limite per eccesso della funzione per x che
tende ad 1. E' facile verificare che i due limiti sono uguali ed il loro valore è proprio 3.
x+2
x+2
lim
=
=3
x
x
−.
+.
x →1
x →1
lim
Continuità in un intervallo
Una funzione Y = f(x) si dice continua in un intervallo se risulta essere continua in ogni punto
dell'intervallo.
E' evidente che per verificare la continuità di una funzione in un intervallo non è immaginabile
applicare la regola usata per la continuità in un punto a tutti gli infiniti punti dell'intervallo.
E' possibile, invece, rifarsi alla seguente regola:
Ogni funzione ottenuta come somma, differenza, prodotto o quoziente di funzioni continue nei
rispettivi domini, risulta essere a sua volta continua nel proprio dominio.
Esempio
Consideriamo la funzione f1(x) = x2 – 1 e la funzione f2 = x.
La funzione f1 è certamente continua nel suo dominio R, in quanto razionale intera di secondo
grado (parabola).
La funzione f2 è certamente continua nel suo dominio R, in quanto razionale intera di primo grado
(retta).
In base alla regola enunciata possiamo allora affermare che le seguenti funzioni risultano continue
nei rispettivi domini:
f3 = f1 + f2 = x2 – 1 + x
nel dominio D = R
f4 = f1 - f2 = x2 – 1 – x
nel dominio D = R
f5 = f1 * f2 = (x2 – 1) * x
nel dominio D = R
f
f=1=
f
6
2
x 2−1
x
nel dominio D = R - {0}
Punti di discontinuità
Una funzione sarà discontinua in un punto se non vale l'uguaglianza sulla quale si basa la
continuità.
Essendo un'uguaglianza a 3 (limite sinistro, limite destro e valore della funzione) è ovvio che essa
può fallire per vari motivi:
1. Il punto potrebbe essere al di fuori del dominio della funzione e, di conseguenza, il valore
f(a) potrebbe non essere calcolabile.
2. I valori del limite sinistro e destro potrebbero essere uguali fra loro, ma diversi da f(a).
3. I valori del limite sinitro e destro potrebbero essere diversi.
Negli esercizi sullo studio delle discontinuità è sempre necessario stabilire quali sono i punti in cui
la funzione è discontinua ed il motivo.
Esempio 1
Consideriamo la funzione f6 dell'esempio precedente che abbiamo visto essere continua in tutto il
suo dominio D = R – {0}.
La funzione risulta quindi discontinua nel punto x = 0. Il motivo è da ricondurre al
f ( x )=
x 2−1 motivo 1. del precedente elenco. Il valore 0, infatti, non fa parte del dominio della
x
funzione e, di conseguenza, il valore f(0) non è calcolabile.
Esempio 2
{3x
se x≠1
Consideriamo la funzione definita a tratti f ( x )=
ed osserviamo che il suo
1 se x=1
dominio è D = R.
Inoltre possiamo facilmente verificare che la funzione coincide con la retta y = 3x per ogni x
diversa da 1, ed è quindi continua in tale intervallo.
Resta da capire cosa accade per x = 1. Per indagare la natura di tale punto si prova ad applicare
la regola di continuità, calcolando i limiti destro e sinistro e verificando se coincidono con il valore
della funzione.
Dopo il calcolo possiamo osservare che la funzione non è continua nel punto x = 1 per il motivo 2.
dell'elenco precedente.
Infatti avremo:
lim f ( x)
lim f ( x)
=
=3
−.
x →1
x → 1+.
mentre f(1) = 1
I limiti destro e sinistro sono uguali tra loro, ma diversi dal valore della funzione.
Esempio 3
Consideriamo la funzione
f (x )=
1
ed osserviamo che il suo dominio D = R – {2}
x−2
Il numeratore è una costante e quindi continua su tutto R; il denominatore è una razionale intera di
primo grado (retta) e quindi continua su tutto R. La funzione f(x) è quindi continua in ogni punto del
suo dominio D. Calcolando i limiti destro e sinistro possiamo osservare che essi sono diversi:
lim f ( x)=−∞
lim f ( x)=+∞
mentre
−.
x →2
x → 2+.
Tipi di discontinuità
Le discontinuità in un punto non sono tutte uguali ma si distinguono in 3 specie in base a cosa
accade nel calcolo del limite destro e del limite sinistro:
Discontinuità di 1a specie (salto)
Nel punto x = a, si ha una discontinuità di prima specie se i limiti sinistro e destro sono diversi ed
entrambi finiti.
lim f ( x)= L1
x → a −.
lim f ( x)= L2
Con L1≠L2
x → a +.
Questo tipo di discontinuità viene anche detta "salto" perchè la quantità S = | L2 – L1 |
rappresenta l'entità del distacco tra le due funzioni nel punto x = a.
Esempio
{3x
se x≤1
Consideriamo la funzione f ( x )=
ed osserviamo che è una funzione definita a
−2x
se x>1
tratti.
Entrambi i tratti sono rappresentati da funzioni razionali intere di primo grado (rette) e quindi
continue su tutto R.
L'unico punto da indagare, quindi, è x = 1
Calcoliamo il limite destro e il limite sinistro
lim −2x=−2 e lim 3x=3
+.
−.
x →1
x →1
I due limiti sono diversi ma finiti, quindi la discontinuità è di prima specie ed il salto è S = 5
Nel seguente grafico possiamo osservare l'andamento della funzione intorno al punto x = 1.
Discontinuità di 2a specie
Nel punto x = a, si ha una discontinuità di seconda specie se almeno uno tra il limite sinistro e il
limite destro è infinito.
lim f ( x)= L
lim f ( x)=±∞
e
−.
x →a
x → a +.
oppure
lim f ( x)= L
lim f ( x)=±∞
e
−.
x → a +.
x →a
oppure
lim f ( x)=±∞
lim f ( x)=±∞
e
−.
x → a +.
x →a
Esempio
x+2
Consideriamo la funzione y=
ed osserviamo che è una funzione ottenuta dal quoziente
x−1 primo grado (rette) e quindi continue su tutto R. La
di due funzioni polinomiali di
funzione risulta quindi continua nel suo dominio D = R – {1}.
L'unico punto da indagare, quindi, è x = 1
Calcoliamo il limite sinistro e il limite destro:
x+2
x+2
=−∞
lim
=+∞
x−1
x−1
e
I due limiti sono infiniti e quindi la discontinuità è di
−.
+.
seconda specie.
x →1
x →1
lim
Nel seguente grafico possiamo osservare l'andamento della funzione intorno al punto x = 1.
Discontinuità di 3a specie
Nel punto x = a, si ha una discontinuità di terza specie se i limiti sinistro e destro sono uguali ed
entrambi finiti.
lim f ( x)= L
x → a −.
lim f ( x)= L
x → a +.
Questo tipo di discontinuità viene anche detta "eliminabile", vedremo con un esempio il perchè di
questa definizione e come si riesca ad eliminare la discontinuità.
Esempio
x 2−1
Consideriamo la funzione y=
ed osserviamo che è una funzione ottenuta dal
x−1 polinomiali di secondo (parabola) e di primo grado (retta)
quoziente di due funzioni
e quindi continue su tutto R. La funzione risulta quindi continua nel suo dominio D = R – {1}.
L'unico punto da indagare, quindi, è x = 1
Calcoliamo il limite sinistro e il limite destro:
x 2−1 0
=
x−1 0 Risolvendo la forma indeterminata otteniamo
−.
x →1
lim
lim x+1=2
−.
x →1
2
x −1 0
lim x+1=2
=
x−1 0 Risolvendo la forma indeterminata otteniamo
+.
x →1
+.
x →1
lim
I due limiti sono uguali e finiti quindi la discontinuità è di terza specie.
Nel seguente grafico possiamo osservare l'andamento della funzione intorno al punto x = 1.
Questa specie di discontinuità viene definita "eliminabile" in quanto è possibile ridefinire la funzione
in modo che la funzione risulti essere continua nel punto considerato, eliminando, di fatto, la
discontinuità.
In questo esempio possiamo ridefinire la funzione come segue:
{
2
x −1
y= x−1
2
se x≠1
se x=1
La funzione ottenuta è definita a tratti: il primo tratto riprende fedelmente la funzione di partenza,
conservando la continuità in ogni suo punto di competenza (x ≠ 1).
Nel punto x = 1, la discontinuità viene eliminata assegnando alla funzione il valore esattamente
uguale al risultato dei limiti destro e sinistro precedentemente calcolato. In questo modo riusciamo
a rendere vera la regola di continuità della funzione nel punto x = 1:
limite sinistro = limite destro = valore della funzione.
Gli asintoti
Strettamente legato alla continuità di una funzione è possibile analizzare l'eventualità che la
funzione presenti uno o più andamenti asintotici.
Si definisce asintoto una retta alla quale il tracciato grafico della funzione tende ad avvicinarsi
senza mai raggiungerla.
In relazione alle caratteristiche grafiche ed algebriche della retta possiamo avere:
•
•
•
Asintoto Verticale:
Asintoto Orizzontale:
Asintoto Obliquo:
la retta è verticale e la sua equazione è del tipo x = k.
la retta è orizzontale e la sua equazione è del tipo y = k.
la retta è obliqua e la sua equazione è del tipo y = mx+q.
Asintoto Verticale
Una retta di equazione x = k rappresenta un asintoto verticale per la funzione y = f(x) se si
verificano le seguenti condizioni:
•
•
il valore k è escluso dal dominio della funzione
limite sinistro e/o limite destro della funzione per x che tende a k non è finito.
Esempio
Si consideri la funzione
y=
1
e verifichiamo la presenza di eventuali asintoti verticali.
x−1
Iniziamo osservando che il dominio della funzione data è D = R -{1}. Di conseguenza la funzione
ha, potenzialmente un asintoto verticale nel punto di ascissa x = 1.
Andiamo a verificare l'andamento della funzione per x che tende a 1 per difetto.
1
1
= =−∞
x−1 0−.
x → 1−.
lim
Andiamo a verificare l'andamento della funzione per x che tende a 1 per eccesso.
1
1
= +. =+∞
x−1 0
x → 1+.
lim
Come possiamo osservare esitono le condizioni per poter affermare che la retta di equazione x = 1
è un asintoto verticale per la funzione data.
N.B. In questo caso l'asintoto viene definito "Bilatero" in quanto entrambi i limiti non sono finiti.
Nel grafico seguente una rappresentazione che evidenzia la presenza dell'asintoto.
Asintoto Orizzontale
Una retta di equazione y = k rappresenta un asintoto orizzontale per la funzione y = f(x) se si
verificano le seguenti condizioni:
•
•
i termini +∞ e/o -∞ non sono esclusi dal dominio della funzione
limite per x che tende a +∞ e/o -∞ è finito e vale k
Esempio
Si consideri la funzione
y=
2x+1
e verifichiamo la presenza di eventuali asintoti orizzontali:
x−1
Iniziamo osservando che il dominio della funzione data è D = R -{1}. Di conseguenza i termini +∞ e
-∞ non sono esclusi dal dominio della funzione.
Andiamo a verificare l'andamento della funzione per x che tende a +∞.
2x+1
= ∞
∞ = 2
x−1
x →+∞
lim
Andiamo a verificare l'andamento della funzione per x che tende a -∞.
2x+1
= ∞
∞ = 2
x−1
x →−∞
lim
Come possiamo osservare esitono le condizioni per poter affermare che la retta di equazione y = 2
è un asintoto orizzontale per la funzione data.
N.B. Anche in questo caso l'asintoto viene definito "Bilatero" in quanto entrambi i limiti rispettano la
definizione data.
Nel grafico seguente una rappresentazione che evidenzia la presenza dell'asintoto per x che tende
a -∞.
Asintoto Obliquo
Una retta di equazione y = mx + q rappresenta un asintoto obliquo per la funzione y = f(x) se si
verificano le seguenti condizioni:
•
i termini +∞ e/o -∞ non sono esclusi dal dominio della funzione
•
Esiste finito
m = lim
f ( x)
x
x →∞
•
Esiste finito
q = lim f ( x)−mx
x →∞
Esempio
Si consideri la funzione
y=
2x 2+1 e verifichiamo la presenza di eventuali asintoti orizzontali:
x−1
Iniziamo osservando che il dominio della funzione data è D = R -{1}. Di conseguenza i termini +∞ e
-∞ non sono esclusi dal dominio della funzione.
Andiamo a calcolare i possibili valori di m e di q.
m = lim
2x 2+1
2x 2+1
= 2
= 2
x (x−1)
x −x
x →∞
Il valore di m esiste, quindi possiamo procedere con il calcolo del valore di q
q = lim
2x 2+1
2x+1
−2x =
= 2
x−1
x−1
x →∞
Anche il valore di q esiste per cui sussitono le condizioni per poter affermare che la retta di
equazione y = 2x + 2 è un asintoto obliquo per la funzione data.
Nel grafico seguente una rappresentazione che evidenzia la presenza dell'asintoto.