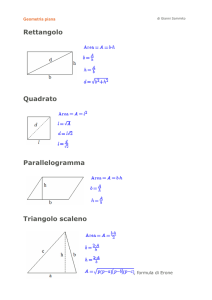
BOOK IN PROGRESS
MATEMATICA
GEOMETRIA
SECONDO ANNO
TOMO NR. 1
SOMMARIO DEL TOMO 1 – SECONDO ANNO
UNITÀ 6: LA CIRCONFERENZA E IL CERCHIO
6.1 Generalità
pag. 1
6.2 Simmetrie nella circonferenza e nel cerchio
pag. 3
6.3 Le parti della circonferenza e del cerchio
pag. 5
6.4 Proprietà delle corde di una circonferenza
pag. 11
6.5 Reciproche posizioni fra retta e circonferenza
pag. 23
6.6 Reciproche posizioni fra due circonferenze
pag. 27
6.7 Angoli alla circonferenza e corrispondenti angoli al centro
pag. 33
6.8 Tangenti condotte da un punto ad una circonferenza
pag. 41
ESERCIZI UNITÀ 6
Conoscenza e comprensione
pag. 47
Applicazione
pag. 54
Problemi. Corde e archi
pag. 61
Reciproche posizioni fra retta e circonferenza. Reciproche
posizioni fra due circonferenze
pag. 63
Angoli al centro e angoli alla circonferenza. Tangenti a una
circonferenza
pag. 65
Problemi di riepilogo
pag. 68
OLIMPIADI
pag. 71
UNITÀ 7: POLIGONI INSCRITTI E CIRCOSCRITTI. POLIGONI REGOLARI
7.1 Generalità
pag. 74
7.2 Punti notevoli di un triangolo
pag. 75
7.3 I quadrilateri inscritti e circoscritti
pag. 86
7.4 I poligoni regolari
pag. 96
ESERCIZI UNITÀ 7
Conoscenza e comprensione
pag. 104
Applicazione
pag. 109
1
Punti notevoli di un triangolo
pag. 111
Quadrilateri inscritti e circoscritti
pag. 112
Poligoni regolari
pag. 113
Problemi di riepilogo
pag. 114
OLIMPIADI
pag. 117
UNITÀ 8: L’ EQUIVALENZA DEI POLIGONI
8.1 Figure equivalenti
pag. 121
8.2 Somma e differenza di superfici
pag. 123
8.3 Poligoni equivalenti
pag. 129
8.4 Costruzione di poligoni equivalenti
pag. 139
8.5 I teoremi di Pitagora e di Euclide
pag. 144
8.6 Espressioni metriche dei teoremi di Pitagora e di Euclide
pag. 152
8.7 Aree dei poligoni – Area del cerchio
pag. 155
8.8 Applicazioni del teorema di Pitagora
pag. 157
8.9 Relazioni tra i lati dei poligoni regolari e i raggi delle circonferenze
inscritte e circoscritte
pag. 164
ESERCIZI UNITÀ 8
Conoscenza e comprensione
pag. 173
Costruzioni
pag. 180
Problemi
pag. 182
Primo teorema di Euclide
pag. 186
Teorema di Pitagora
pag. 187
Secondo teorema di Euclide
pag. 188
Problemi di riepilogo sull’equivalenza
pag. 189
Problemi sulle aree dei poligoni. Espressioni metriche dei teoremi di
pag. 191
Pitagora e di Euclide.
OLIMPIADI
pag. 195
2
UNITÀ 6
LA CIRCONFERENZA E IL CERCHIO
6.1 Generalità
Fissati nel piano un punto O ed un segmento r , si chiama circonferenza di centro O e raggio r il
luogo geometrico dei punti P del piano aventi distanza da O congruente al segmento r (fig. 1):
.P
.
//
.
O
//
r
.
PO = distanza di P da O = d (P, O)
PO ≅ r
fig. 1
Ovviamente ogni segmento avente per estremi il punto O ed un punto qualsiasi della circonferenza è
congruente al segmento r (e quindi tutti i raggi sono congruenti).
Si chiama corda il segmento che ha per estremi due punti qualsiasi della circonferenza (fig. 2):
Q
.
P.
.
PQ corda
O
fig. 2
Si chiama diametro ogni segmento che ha per estremi due punti della circonferenza e che contiene il
centro della circonferenza stessa (fig. 3):
A.
r
.
O
r
AB diametro
.B
AB ≅ 2 r
fig. 3
Il diametro è, quindi, una corda che contiene il centro della circonferenza. Gli estremi A e B del
diametro si dicono punti diametralmente opposti. La retta passante per A e B viene detta retta
diametrale.
3
Dato che il diametro è congruente al doppio del raggio, tutti i diametri di una stessa circonferenza
sono congruenti.
Le circonferenze si disegnano con il compasso: la punta metallica nel centro O ed apertura “uguale” al
raggio.
DISEGNA sul tuo quaderno tre circonferenze con centri in tre punti a tua scelta e raggi r = 3 cm,
r = 5 cm, r = 6 cm.
La circonferenza è una linea chiusa non intrecciata e divide il piano in tre sottoinsiemi disgiunti:
l’insieme dei punti la cui distanza dal centro è minore del raggio (punti interni alla
circonferenza);
l’insieme dei punti la cui distanza dal centro è congruente al raggio (punti della circonferenza);
l’insieme dei punti la cui distanza dal centro è maggiore del raggio (punti esterni alla
circonferenza).
In fig. 4 è data una circonferenza Γ e sono rappresentati un punto interno, un punto esterno e un punto
appartenente a Γ:
Q.
O
.
Q punto interno a Γ :
.P
OQ < r
P punto appartenente a Γ : OP ≅ r
T punto esterno a Γ :
OT > r
Γ
.T
fig. 4
Si dice cerchio di centro O e raggio r il luogo dei punti P del piano che hanno distanza da O minore o
congruente al raggio; in simboli:
{P∈ π /
PO < r ∨ PO ≅ r}.
Pertanto, il cerchio è la figura formata dall’insieme dei punti interni e dei punti appartenenti alla
circonferenza (fig. 5):
circonferenza
cerchio
La circonferenza è il contorno del cerchio.
.
O
Il punto O è il centro della circonferenza e del cerchio.
fig. 5
Il cerchio è una figura convessa [PERCHÉ?]
È intuitivo che due circonferenze/cerchi sono congruenti se e solo se hanno raggi congruenti.
4
6.2 Simmetrie nella circonferenza (e nel cerchio)
La circonferenza e il cerchio hanno infiniti assi di simmetria e un centro di simmetria.
Valgono infatti i seguenti teoremi:
TEOREMA
Ogni retta che contiene un diametro è asse di simmetria per la circonferenza / il cerchio.
Sia data una circonferenza Γ di centro O e raggio r. Consideriamo un diametro AB e la simmetria
assiale σAB di asse la retta AB.
Vogliamo dimostrare che, considerato un generico punto P di Γ, il suo corrispondente P', nella σAB,
appartiene ancora a Γ.
Quindi:
P.
Γ circonferenza di centro O
Hp.:
A
.
.
.
O
Γ
A, B, P ∈ Γ ; O ∈ AB
σAB : P → P'
B
Th.:
P' ∈ Γ
Dimostrazione
Nella σAB si ha:
σAB : O → O
perché O è un punto dell’asse di simmetria
e, poiché per ipotesi:
σAB : P → P' ,
si ha:
σAB : OP → OP' .
Dato che la simmetria assiale è una isometria, si ha:
OP ≅ OP'
e, poiché OP ≅ r, segue che:
OP' ≅ r
per la proprietà transitiva della congruenza,
cioè P' ∈ Γ .
5
[La figura seguente “sintetizza” il precedente teorema:
P.
*
A
.
.
.
O
B
*
.
Γ
P'
]
C.V.D.
Dal precedente teorema segue che la circonferenza e il cerchio hanno infiniti assi di simmetria che
sono le infinite rette passanti per il centro (rette del fascio di centro O), cioè le infinite rette che
“contengono” gli infiniti diametri.
TEOREMA
Il centro della circonferenza è centro di simmetria per la circonferenza / il cerchio.
Data la circonferenza Γ di centro O e raggio r, consideriamo la simmetria centrale di centro O, σo.
Vogliamo dimostrare che, considerato un generico punto A di Γ, il suo corrispondente nella σo
appartiene ancora a Γ.
Quindi:
Γ circonferenza di centro O
A
.
Hp.:
.
O
A∈ Γ
σo : A → A'
Γ
Th.:
A' ∈ Γ
Dimostrazione
Sappiamo per ipotesi che A ∈ Γ e che
σo : A → A' ,
quindi, per definizione di simmetria centrale, è:
OA ≅ OA'
e, poiché OA ≅ r, si ha che:
OA' ≅ r
per la proprietà transitiva della congruenza,
cioè A' ∈ Γ (fig. 6):
6
A.
.
. A'
O
Γ
fig. 6
C.V.D.
PROVA TU:
La circonferenza e il cerchio sono figure unite in ogni rotazione di centro O.
6.3 Le parti della circonferenza e del cerchio
Si dice arco ciascuna delle due parti in cui una circonferenza viene divisa da due suoi punti (fig. 7):
.B
A.
.
O
fig. 7
I punti A e B individuano due archi che si indicano con AB.
Spesso, per evitare confusione, si fissa un punto interno ad uno dei due archi che si vuole individuare
(fig. 8):
P
.
A.
.B
.
O
.
Q
fig. 8
Si hanno così gli archi APB e AQB; oppure, se vogliamo riferirci per esempio all’arco APB, diciamo
l’arco AB che contiene P o, ancora, l’arco AB che non contiene Q.
Alcuni parlano di “arco minore” / “arco maggiore”, ….. con qualche problema, però, nel caso in
cui gli estremi dell’arco siano punti diametralmente opposti.
7
Ad ognuno dei due archi individuati da due punti A e B della circonferenza “corrisponde” una sola
corda AB (corda sottesa dall’arco) ma ad ogni corda “corrispondono” due archi AB (archi sottesi
dalla corda) [fig. 9]:
.B
A.
.
O
fig. 9
o La corda AB è sottesa da ciascuno dei due archi AB.
o I due archi AB sono sottesi dalla corda AB.
Quando i due punti A e B sono diametralmente opposti, ognuno dei due archi viene chiamato
semicirconferenza (fig. 10):
.
A.
O
.B
semicirconferenza
fig. 10
Ogni corda divide il cerchio in due parti, ciascuna delle quali si chiama segmento circolare ad una
base.
In fig. 11, la corda AB delimita due segmenti circolari di base AB:
A.
segmento circolare di base AB
.B
.
segmento circolare di base AB
O
fig. 11
OSSERVAZIONE:
Il segmento circolare a una base si può pensare ottenuto dall’intersezione di un semipiano, la cui
origine contiene una corda, con un cerchio (fig. 12):
8
A .
.
B
.
O
fig. 12
Si dice altezza di un segmento circolare ad una base il segmento che ha come estremi il punto medio
della base e il punto d’intersezione dell’asse della base con la circonferenza (meglio, con l’arco del
nostro segmento circolare).
In fig. 13 abbiamo individuato un segmento circolare di base AB e altezza MH:
A.
H
.
*
.
M *
.B
.
O
fig. 13
Se la corda è un diametro (fig. 14), ognuno dei due segmenti circolari viene chiamato semicerchio:
.
A
O
Il semicerchio è ciascuna delle due
semicerchio
B
parti di piano comprese fra una
circonferenza ed un suo diametro.
fig. 14
Se consideriamo due corde parallele AB e CD, la parte di cerchio compresa tra le due corde si chiama
segmento circolare a due basi (AB e CD basi) [fig. 15]:
C.
A.
.
.D
.B
segmento circolare a due basi
O
fig. 15
9
OSSERVAZIONE:
Il segmento circolare a due basi si può pensare ottenuto dall’intersezione di una striscia, individuata da
due corde parallele (basi del segmento circolare) con un cerchio (fig. 16):
C.
A
.D
.
.
.
B
O
fig. 16
Si chiama altezza di un segmento circolare a due basi la distanza tra le due basi (fig. 17):
C.
A. .
H
.D
.B
.
CH altezza del segmento circolare
O
di basi AB e CD.
fig. 17
Si dice angolo alla circonferenza un angolo convesso avente per vertice un punto della circonferenza
e i lati entrambi secanti la circonferenza (fig. 18), oppure uno secante e l’altro tangente (fig. 19):
B
.
A.
.O
BAC angolo alla circonferenza.
.
I lati AB e AC sono entrambi secanti la circonferenza.
C
fig. 18
L’angolo alla circonferenza individua l’arco BC di colore rosso: si dice che l’angolo alla circonferenza
BAC insiste sull’arco BC;
10
oppure:
D
EDF angolo alla circonferenza.
.
Il lato DF è secante, il lato DE è tangente
E
O
alla circonferenza.
F
fig. 19
L’angolo alla circonferenza individua l’arco DF di colore blu: si dice che l’angolo alla circonferenza
EDF insiste sull’arco DF.
Si dice angolo al centro un angolo che ha il vertice nel centro di una circonferenza (fig. 20):
B
.
AOB angolo convesso
.
O
.
A
fig. 20
In fig. 20, i lati dell’angolo al centro intersecano la circonferenza in due punti A e B, individuando,
così, l’arco AB di circonferenza, (e la corda AB), interno all’angolo: si dice che l’angolo al centro
AOB insiste sull’arco AB o sottende l’arco AB .
In fig. 21, l’angolo convesso AOB insiste sull’arco AB di colore rosso mentre l’angolo concavo AOB
insiste sull’arco AB di colore blu.
B
.
.
O
.
A
fig. 21
11
OSSERVAZIONE:
Ad ogni angolo alla circonferenza “corrisponde” uno ed un solo angolo al centro che insiste sullo
stesso arco (fig. 22):
A
BAC angolo alla circonferenza che insiste
sull’arco BC.
O
.
All’angolo BAC → uno ed un solo angolo
B
al centro, l’angolo BOC, che insiste sullo
stesso arco BC.
C
fig. 22
La “corrispondenza” evidenziata non è però biunivoca; infatti ad un angolo al centro che insiste su un
certo arco, corrispondono infiniti angoli alla circonferenza che insistono sullo stesso arco (fig. 23):
A1
BOC angolo al centro che insiste sull’arco BC.
A
A2
BAC
angolo
circonferenza
O
.
alla
che
insiste sull’arco BC;
B
BA1C angolo alla
C
fig. 23
All’angolo BOC
circonferenza
che
insiste sull’arco BC;
BA2C angolo alla
circonferenza
che
insiste sull’arco BC;
……………….......
PROVA TU il seguente
TEOREMA
In ogni circonferenza se si verifica una delle seguenti congruenze:
•
due corde sono congruenti;
•
due archi sono congruenti;
•
due angoli al centro sono congruenti,
allora si verificano anche le restanti congruenze.
12
Si dice settore circolare ciascuna delle due parti di cerchio limitate da due raggi (fig. 24):
B
.
Ciascuna delle due parti colorate è un settore circolare
. α
.
O
α ampiezza del settore di colore fucsia.
A
fig. 24
OSSERVAZIONE:
Il settore circolare si può pensare ottenuto dall’intersezione di un angolo al centro con il cerchio (fig.
25):
B
.
.
O
.
A
fig. 25
6.4 Proprietà delle corde di una circonferenza
TEOREMA
In una circonferenza, ogni diametro è maggiore di qualsiasi corda non passante per il centro.
D
.
Γ circonferenza di centro O
C.
A.
.
O
Γ
.B
Hp.:
AB diametro
CD corda , O ∉ CD
Th.:
AB > CD
Dimostrazione
Congiungiamo gli estremi C e D della corda con il centro O della nostra circonferenza ottenendo, così,
il triangolo COD (fig. 26):
13
D
.
C.
.
A.
.B
O
Γ
fig. 26
Poiché in un triangolo la somma di due lati è maggiore del terzo lato, si ha:
OC + OD > CD
ed essendo OC e OD raggi, risulta:
OC + OD ≅ AB
e quindi:
AB > CD
C.V.D.
TEOREMA
In una circonferenza, l’asse di una corda passa per il centro della circonferenza stessa.
C.
Γ circonferenza di centro O
Hp.:
AB corda
CD asse di AB
A.
*
.
.
Γ
M *
.B
Th.:
CD diametro
D
Dimostrazione
Sappiamo che CD è l’asse della corda AB, cioè la perpendicolare ad AB passante per il suo punto
medio M.
Per dimostrare che CD è un diametro, basta far vedere che vi appartiene il centro O.
Ora, il centro della circonferenza è, per definizione, equidistante da tutti i punti della circonferenza e,
quindi, anche dagli estremi A e B della corda (fig. 27):
C
.
r
A.
*
Γ
.O
.
r
M *
.
D
.B
fig. 27
14
Pertanto il centro O appartiene all’asse di AB [ricorda che “l’asse di un segmento è il luogo dei punti
del piano equidistanti dagli estremi del segmento”].
C.V.D.
CIRCONFERENZA PER TRE PUNTI
Come conseguenza del precedente teorema si ha il seguente:
TEOREMA
Per tre punti non allineati passa una ed una sola circonferenza.
A.
Hp.: A, B, C punti non allineati
B.
Th.:
∃ circonferenza passante
per A, B, C
C.
Dimostrazione
Conduciamo gli assi dei segmenti AB e BC ed indichiamo con O il loro punto d’intersezione (esiste!
PERCHÉ?) [fig. 28]:
A.
M .
B.
*
.O
.
N*
.C
fig. 28
Si ha:
OA ≅ OB
perché O appartiene all’asse di AB;
OB ≅ OC
perché O appartiene all’asse di BC,
da cui segue:
OA ≅ OB ≅ OC
per la proprietà transitiva della congruenza.
Pertanto O è equidistante dai punti A, B, C e, quindi, è il centro della circonferenza passante per tali
punti (fig. 29):
15
.A
r
B.
r
.O
r
.
C
fig. 29
La circonferenza è unica perché è unico il punto d’intersezione dei due assi e, di conseguenza, è unico
il punto equidistante dai punti dati.
C.V.D.
OSSERVAZIONE:
Per la dimostrazione del teorema si possono condurre due qualsiasi tra i tre assi dei tre segmenti AB,
BC, AC.
COROLLARIO 1
Due circonferenze distinte non possono avere più di due punti di intersezione.
[Infatti se ne avessero tre, sarebbero la stessa circonferenza].
COROLLARIO 2
Una circonferenza non può avere tre punti allineati.
[Se una circonferenza avesse, infatti, tre punti allineati:
.O
.
.
.
A
B
C
A, B, C allineati
CONTINUA
gli assi delle corde AB e BC dovrebbero essere incidenti in O, per cui ……………………………....
……………………………………………………………………].
16
Ora giochiamo ….. con un po’ di circonferenze e “verifichiamo” con il disegno che:
per un punto del piano passano infinite circonferenze.
Dato, infatti, nel piano un punto P, osserviamo che ognuno degli infiniti punti O1, O2, O3, ….. ,
distinti da P, può essere considerato come centro di una circonferenza Γ1 , Γ2 , Γ3 , ….., di raggio
rispettivamente O1P , O2P , O3P , ….. (fig. 30):
Γ4
Γ2
.
.
O4 .
P
.
O2
O5
.
O1
.
O3
Γ1
Γ3
fig. 30
per due punti del piano passano infinite circonferenze.
Dati, infatti, nel piano due punti P e Q, conduciamo l’asse del segmento PQ ed osserviamo che
ognuno degli infiniti punti O1, O2, O3, … dell’asse può essere considerato come centro di una
circonferenza Γ1, Γ2 , Γ3 , ., di raggio rispettivamente O1P (o O1Q) , O2P (o O2Q) , O3P (o O3Q) , …..
(fig. 31):
Γ2
. O6
.O2
*
P
Γ1
Q
.O
1
*
. O3
. O4
O5 .
Γ3
fig. 31
per tre punti del piano, non allineati, passa una ed una sola circonferenza.
CONTINUA
Dati, infatti, nel piano tre punti L, M, N, non allineati ………………………………………….
(secondo la costruzione riportata in fig. 28, pag. 13).
17
TEOREMA
La perpendicolare condotta dal centro della circonferenza ad una sua corda dimezza la corda.
Γ circonferenza di centro O
Hp.:
.O
OH ⊥ AB
.
A.
AB corda
.B
H
Th.:
Γ
AH ≅ HB
Dimostrazione
Congiungiamo il centro O con gli estremi A e B della corda (fig. 32):
r
.O
r
.B
.
A.
H
Γ
fig. 32
e consideriamo i triangoli OAH e OBH; essi hanno:
OHA ≅ OHB
retti, per ipotesi;
OA ≅ OB
perché raggi;
OH
(o OH ≅ OH per la proprietà riflessiva della congruenza).
in comune
I due triangoli, avendo ordinatamente congruenti l’angolo retto, l’ipotenusa ed un cateto, sono
congruenti per il criterio di congruenza dei triangoli rettangoli. Avranno, pertanto, tutti gli elementi
corrispondenti congruenti, in particolare:
(“segnare AH e HB con il simbolo * ”).
AH ≅ HB
C.V.D.
[Al termine della teorema la figura si presenta come segue:
r
A.
*
Γ
.O
.
H
r
*
.B
]
18
TEOREMA INVERSO
La congiungente il centro O di una circonferenza con il punto medio M di una sua corda è
perpendicolare alla corda.
Γ circonferenza di centro O
.O
A.
*
.
M
Hp.:
*
AB corda
AM ≅ MB
.B
Γ
Th.:
OM ⊥ AB
Dimostrazione
Congiungiamo il centro O con gli estremi A e B della corda (fig. 33):
O
.
r
A.
*
r
.
M *
Γ
.B
fig. 33
e consideriamo i triangoli OAM e OBM; essi hanno:
AM ≅ MB
per ipotesi;
OA ≅ OB
perché raggi;
OM
(o OM ≅ OM per la proprietà riflessiva della congruenza).
in comune
I due triangoli, avendo ordinatamente congruenti i tre lati, sono congruenti per il terzo criterio di
congruenza dei triangoli. Avranno, pertanto, tutti gli elementi corrispondenti congruenti, in
particolare:
AMO ≅ BMO
ed essendo AMB piatto, si ha che gli angoli AMO e BMO sono retti e quindi:
OM ⊥ AB .
C.V.D.
[Questa volta, ... e quasi sempre in seguito, COMPLETA TU la figura].
19
TEOREMA
In una stessa circonferenza (o in circonferenze congruenti) corde congruenti hanno la stessa
distanza dal centro.
[Dimostriamo il teorema nel caso in cui le due corde appartengono alla stessa circonferenza].
D
.
Γ circonferenza di centro O
K.
~
C.
AB, CD corde
.O
A.
Hp.:
Γ
OH ⊥ AB
.B
~H.
AB ≅ CD
OK ⊥ CD
Th.:
OH ≅ OK
Dimostrazione
Osserviamo che le perpendicolari OH e OK, condotte da O alle corde, tagliano le corde nel loro punto
medio (teorema pag. 16), per cui:
perché metà di corde congruenti (“segnare AH, HB, CK e KD con il
AH ≅ HB ≅ CK ≅ KD
simbolo * ”).
Congiungiamo, ora, il centro O con gli estremi A e C (fig. 34):
D
.
C.
~K.
*
r
*
.O
r
A. *
Γ
.
~
H
*
.B
fig. 34
e consideriamo i triangoli OAH e OCK; essi hanno:
OHA ≅ OKC
retti, per ipotesi;
OA ≅ OC
perché raggi;
AH ≅ CK
per precedente osservazione.
I due triangoli, oltre all’angolo retto, hanno ordinatamente congruenti l’ipotenusa ed un cateto per cui
sono congruenti per il criterio di congruenza dei triangoli rettangoli. Avranno, pertanto, tutti gli
elementi corrispondenti congruenti, in particolare:
OH ≅ OK .
C.V.D.
Si effettua un’analoga dimostrazione se le corde appartengono a due circonferenze congruenti (questa
considerazione vale anche per i teoremi successivi).
20
TEOREMA INVERSO
In una stessa circonferenza (o in circonferenze congruenti) se due corde hanno la stessa distanza
dal centro, allora sono congruenti.
[Dimostriamo il teorema nel caso in cui le due corde appartengono alla stessa circonferenza]
D
.
Γ circonferenza di centro O
K.
C.
AB, CD corde
*
Hp.:
.O
*
A.
H
Γ
OK distanza di O da CD
.B
.
OH distanza di O da AB
OH ≅ OK
Th.:
AB ≅ CD
Dimostrazione
Congiungiamo il centro O con gli estremi A e C (fig. 35):
D
.
K.
C.
*
r
r
A.
.O
*
.
Γ
H
.B
fig. 35
e consideriamo i triangoli OAH e OCK; essi hanno:
OHA ≅ OKC ( ≅ 90°)
perché OH e OK distanze di O rispettivamente da AB e CD;
OA ≅ OC
perché raggi;
OH ≅ OK
per ipotesi.
I due triangoli, avendo ordinatamente congruenti l’angolo retto, l’ipotenusa ed un cateto, sono
congruenti per il criterio di congruenza dei triangoli rettangoli. Avranno, pertanto, tutti gli elementi
corrispondenti congruenti, in particolare:
AH ≅ CK.
Infine, poiché le perpendicolari condotte dal centro alle corde dividono ogni corda in due segmenti
congruenti, si deduce che, se le metà sono congruenti, saranno congruenti anche le corde stesse; cioè:
AB ≅ CD .
C.V.D.
21
TEOREMA
Se in una stessa circonferenze (o in circonferenze congruenti) due corde non sono congruenti,
allora anche le loro distanze dal centro non sono congruenti e, in particolare, la corda maggiore
ha distanza minore.
[Dimostriamo il teorema nel caso in cui AB e CD siano due corde della stessa circonferenza di centro
O, con AB > CD]
B
H
A
Γ circonferenza di centro O
Hp.:
.O
AB > CD
OH ⊥ AB
OK ⊥ CD
C
Γ
K
Th.:
D
OK > OH
Dimostrazione
Se le due corde non sono consecutive, “costruiamo” la corda BE consecutiva ad AB e cogruente a CD
(fig. 36):
B
H
A
.O
C
E
Γ
K
D
fig. 36
e diciamo OT la distanza di BE da O (fig. 37):
B
H
A
.
T
O
C
E
Γ
K
D
fig. 37
22
Poiché le corde CD e BE sono congruenti, si ha che le loro distanze dal centro sono congruenti
(teorema pag. 18), cioè OK ≅ OT.
Inoltre, da:
AB > CD ∧ CD ≅ BE
segue, per la proprietà della disuguaglianza tra segmenti, che:
AB > BE
e la stessa relazione vale fra le metà delle due corde, cioè:
BH > BT
(PERCHÈ BH è la metà di AB e BT la metà di BE?)
Consideriamo ora il triangolo BHT (fig. 38):
B
H
A
.
T
O
C
E
Γ
K
D
fig. 38
e osserviamo che, poiché in un triangolo al lato maggiore sta opposto l’angolo maggiore
(disuguaglianza triangolare), si ha:
(“segnare BTH e BHT rispettivamente con i simboli
BTH > BHT
.
e
”)
[fig. 39]:
B
H
A
.
.
T
O
C
E
Γ
K
D
fig. 39
23
per cui fra gli angoli HTO e THO, complementari rispettivamente degli angoli BTH e BHT, vale la
relazione opposta, cioè:
HTO < THO
e quindi:
OH < OT
perché nel triangolo HOT ad angolo minore si oppone lato minore,
che è lo stesso dire:
OH < OK
C.V.D.
TEOREMA INVERSO
Se in una stessa circonferenza (o in circonferenze congruenti) due corde hanno distanze dal
centro non congruenti, allora anche le corde non sono congruenti e, in particolare, è maggiore la
corda che ha distanza minore da esso.
PROVA TU a dimostrare il teorema, sempre nel caso in cui le due corde AB e CD appartengono alla
stessa circonferenza di centro O e la distanza di AB da O sia minore di quella di CD da O.
Riferisci, quindi, la dimostrazione alla seguente figura e ai dati riportati:
B
H
A
Γ circonferenza di centro O
Hp.:
.O
OH ⊥ AB
OK ⊥ CD
OH < OK
Γ
C
K
D
Th.:
AB > CD
(suggerimento: se le due corde non sono consecutive, “costruisci” la corda BE consecutiva a ….. e
congruente a ….. . Dimostrazione per assurdo)
24
6.5 Reciproche posizioni fra retta e circonferenza
Date la circonferenza Γ, di centro O e raggio r, ed una retta s, vogliamo studiare le posizioni che la
retta può assumere rispetto alla circonferenza.
Tracciamo dal centro O la perpendicolare OH alla retta s. Si possono presentare i seguenti casi:
1. retta esterna alla circonferenza (fig. 40):
Γ
.O
OH > OA
.
A
cioè
OH > r
s
.
H
fig. 40
COMPLETA:
In tal caso il punto H è esterno alla circonferenza e ogni altro punto P appartenente ad s, avendo
distanza da O …………………. di …… , perché il segmento di perpendicolare è ………………..
di ogni segmento ………………. , è …………………. alla circonferenza (fig. 41):
Γ
.O
.
A
.
H
Pertanto:
.
s
P
fig. 41
Γ ∩ s = ……. .
In tal caso la retta è esterna alla circonferenza.
Pertanto:
una retta è esterna ad una circonferenza se la sua distanza dal centro della circonferenza è
maggiore del raggio.
Viceversa:
Se la distanza di una retta dal centro di una circonferenza è maggiore del raggio, allora la retta è
esterna alla circonferenza (PROVA TU)
[e quindi “si ha” una condizione necessaria e sufficiente].
25
2. retta tangente alla circonferenza (fig. 42):
Γ
OH ≅ OA
.O
cioè
OH ≅ r
s
.
H ≡A
fig. 42
COMPLETA:
In tal caso il punto H “sta” sulla circonferenza e ogni altro punto P appartenente ad s, avendo distanza
da O …………………. di …… (perché il segmento di perpendicolare è …………………… di ogni
segmento ………………. , è …………………. alla circonferenza (fig. 43):
Γ
.O
.
H ≡A
.
s
P
fig. 43
Pertanto:
Γ ∩ s = {H}
H si dice punto di tangenza
In questo caso la retta è tangente alla circonferenza.
Pertanto:
una retta è tangente ad una circonferenza se la sua distanza dal centro della circonferenza è
congruente al raggio.
Viceversa:
Se la distanza di una retta dal centro di una circonferenza è congruente al raggio, allora la retta
è tangente alla circonferenza (PROVA TU)
[e quindi “si ha” una condizione necessaria e sufficiente].
26
3. retta secante la circonferenza (fig. 44):
Γ
OH < OA
.O
cioè
OH < r
s
.
H.
A
fig. 44
COMPLETA:
In tal caso il punto H è interno alla circonferenza. Prendiamo, allora, su s un punto P tale che PH ≅ r e
consideriamo il triangolo rettangolo OPH (fig. 45):
Γ
.O
.
P
s
.
H
fig. 45
Si ha che:
OP > … ,
perché, nel triangolo rettangolo OPH, il lato OP è ………………………
e quindi:
…>r,
per cui il punto … è esterno alla circonferenza.
Segue che il segmento HP unisce un punto interno (…) con un punto esterno (…) e pertanto deve
intersecare la ………….….………….. (postulato di continuità), diciamo nel punto E (fig. 46):
Γ
.O
. .
P …
.
s
H
fig. 46
27
Ripetendo lo stesso ragionamento con un punto Q, simmetrico di P rispetto ad H, e quindi tale che
QH ≅ r , si ha che il segmento QH ha un punto F in comune con la circonferenza (fig. 47):
Γ
.O
. .
PE
.
H
. .
s
FQ
fig. 47
Esistono, quindi, due punti E ed F, comuni alla retta s e alla circonferenza. In questo caso la retta s si
dice secante la circonferenza nei punti E ed F.
In simboli:
Γ ∩ s = {E, F} .
Pertanto:
una retta è secante ad una circonferenza se la sua distanza dal centro della circonferenza è
minore del raggio.
Viceversa:
Se la distanza di una retta dal centro di una circonferenza è minore del raggio, allora la retta è
secante la circonferenza (PROVA TU)
[e quindi “si ha” una condizione necessaria e sufficiente].
Tutto quanto detto ci permette di formulare il seguente teorema:
TEOREMA
Condizione necessaria e sufficiente affinchè una retta sia:
esterna ad una circonferenza è che la sua distanza dal centro sia maggiore del raggio;
tangente ad una circonferenza è che la sua distanza dal centro sia congruente al raggio;
secante ad una circonferenza è che la sua distanza dal centro sia minore del raggio.
In conclusione, QUANTI punti, al massimo, possono avere in comune una retta ed una circonferenza?
28
6.6 Reciproche posizioni fra due circonferenze
Date in un piano due circonferenze Γ1 e Γ2 , esaminiamo le possibili reciproche posizioni che esse
possono assumere.
Osserviamo innanzitutto che per tre punti allineati non passa alcuna circonferenza
(COROLLARIO 2, pag. 14), mentre per tre punti non allineati ne passa una sola (TEOREMA
pag. 13).
Pertanto, due circonferenze possono avere al massimo due punti di intersezione (COROLLARIO 1,
pag. 14).
Si possono presentare, quindi, i casi seguenti:
1° caso: circonferenze esterne (fig. 48):
.
r1
O1
r2
.
O2
Γ2
Γ1
fig. 48
Le circonferenze Γ1 e Γ2 sono esterne: la distanza fra i due centri è maggiore della somma dei due
raggi.
In simboli:
O1O2 > r1 + r2
COMPLETA:
Nel caso delle circonferenze esterne, ogni punto di Γ1 è ………………… a Γ2 e ogni …………… di
….. è ………………… a Γ1 .
Quindi:
Γ1 ∩ Γ2 = ……
Si ha:
•
due circonferenze Γ1 e Γ2 sono fra loro esterne se la distanza fra i due centri è maggiore
della somma dei due raggi.
29
Viceversa:
•
se la distanza fra i centri di due circonferenze è maggiore della somma dei due raggi,
allora le due circonferenze sono esterne.
[e quindi “si ha” una condizione necessaria e sufficiente].
2° caso: circonferenze tangenti esternamente (fig. 49):
.
O1
r1
. r2 .
T
O2
Γ2
Γ1
fig. 49
Le circonferenze Γ1 e Γ2 sono tangenti esternamente: la distanza fra i due centri è congruente alla
somma dei due raggi.
In simboli:
O1O2 ≅ r1 + r2
T si dice punto di tangenza
COMPLETA:
Nel caso delle circonferenze Γ1 e Γ2 , esse hanno un unico ……….. comune T, appartenente alla retta
..... ; ogni altro punto di …… è ……………… a Γ2 e ogni altro punto di …… è ……………… a
…… (cioè il centro di ognuna delle due circonferenze è ……………. all’altra).
Quindi:
Γ1 ∩ Γ2 = ……
Si ha:
•
due circonferenze Γ1 e Γ2 sono tangenti esternamente se la distanza fra i centri è
congruente alla somma dei due raggi.
Viceversa:
•
se la distanza fra i centri di due circonferenze è congruente alla somma dei due raggi,
allora le due circonferenze sono tangenti esternamente.
[e quindi “si ha” una condizione necessaria e sufficiente].
30
OSSERVAZIONE:
Nel caso esaminato, le due circonferenze hanno, nel punto T, la stessa retta tangente t che è
perpendicoalre alla congiugente O1O2 (fig. 50):
.
.
O1
Abbiamo “segnato” quattro angoli
.
T
retti; è vero che sono troppi?
O2
Γ2
Γ1
t
fig. 50
3° caso: circonferenze secanti (fig. 51):
A
r1
.
r2
.
.
O2
O1
.
B
Γ1
Γ2
fig. 51
Le circonferenze Γ1 e Γ2 sono secanti: la distanza fra i due centri è minore della somma dei due
raggi e maggiore della loro differenza.
In simboli:
r1 – r2 < O1O2 < r1 + r2
COMPLETA:
Nel caso delle circonferenze secanti, le due circonferenze Γ1 e Γ2 hanno ….. punti, … e … , in
comune e che non appartengono alla congiungente ……. .
Si ha:
•
due circonferenze Γ1 e Γ2 sono secanti se la distanza fra i due centri è minore della
somma dei raggi e maggiore della loro differenza.
Viceversa:
•
se la distanza fra i centri di due circonferenze è minore della somma dei raggi e maggiore
della loro differenza, allora le due circonferenze sono secanti.
[e quindi “si ha” una condizione necessaria e sufficiente].
31
4° caso: circonferenze tangenti internamente (fig. 52):
.
r1
.
.
O1 O2 r2 T
r1 > r2
Γ2
Γ1
fig. 52
Le circonferenze Γ1 e Γ2 sono tangenti internamente: la distanza fra i due centri è congruente alla
differenza dei due raggi.
In simboli:
O1O2 ≅ r1 – r2
T si dice punto di tangenza
COMPLETA:
Nel caso delle circonferenze tangenti internamente, le due circonferenze Γ1 e Γ2 hanno un unico
…….…... comune T, appartenente alla retta …. , e ogni altro punto di …….. è interno a ………… .
Quindi:
Γ1 ∩ Γ2 = ……
Si ha:
•
due circonferenze Γ1 e Γ2 sono tangenti internamente se la distanza fra i due centri è
congruente alla differenza dei due raggi.
Viceversa:
•
se la distanza fra i centri di due circonferenze è congruente alla differenza dei raggi,
allora le due circonferenze sono tangenti internamente.
[e quindi “si ha” una condizione necessaria e sufficiente].
OSSERVAZIONE:
Nel caso esaminato, le due circonferenze hanno, nel punto T, la stessa retta tangente t che è
perpendicolare alla retta O1O2 (fig. 53):
.
.
O1 O2
.
T
Γ2
Γ1
t
32
fig. 53
5° caso: circonferenza una interna all’altra (fig. 54):
.
.
r1
r1 > r2
O1 O2 r2
Γ2
Γ1
fig. 54
La circonferenza Γ2 è interna alla circonferenza Γ1 : la distanza fra i due centri è minore della
differenza dei raggi.
In simboli:
O1O2 < r1 – r2
COMPLETA:
Nel caso della circonferenza Γ2 , interna alla circonferenza Γ1 , si ha che ……….. punto di ….. è
……………. a Γ1 .
Quindi:
Γ1 ∩ Γ2 = ……
Si ha:
•
una circonferenza Γ2 è interna ad una circonferenza Γ1 se la distanza dei loro centri è
minore della differenza dei raggi.
Viceversa:
•
se la distanza fra i centri di due circonferenze è minore della differenza dei raggi, allora
una circonferenza è interna all’altra.
[e quindi “si ha” una condizione necessaria e sufficiente].
Tutto quanto detto ci permette di formulare il seguente teorema:
TEOREMA
Condizione necessaria e sufficiente affinchè due circonferenze siano:
esterne è che la distanza fra i centri sia maggiore della somma dei raggi;
tangenti esternamente è che la distanza fra i centri sia congruente alla somma dei raggi;
secanti è che la distanza fra i centri centri sia minore della somma dei raggi e maggiore della
loro differenza;
tangenti internamente è che la distanza fra i centri sia congruente alla differenza dei raggi;
interne una all’altra è che la distanza fra i centri centri sia minore della differenza dei raggi.
33
Come caso particolare di circonferenze una interna all’altra, si ha quello di due circonferenze che
hanno lo stesso centro (circonferenze concentriche) [fig. 55]:
.
O1 ≡ O2
Γ1
Γ2
fig. 55
La definizione si estende ovviamente ai cerchi concentrici.
Nel caso di due circonferenze concentriche, si definisce corona circolare la parte di piano limitata
dalle due circonferenze (fig. 56):
corona circolare
Γ1
Γ2
fig. 56
In altre parole, la corona circolare è l’insieme dei punti del cerchio di raggio maggiore che sono
esterni a quello di raggio minore.
Riassumendo si ha:
reciproche posizioni di due circonferenze
di raggi r1 e r2 , con r1 > r2
esterne
punti in comune
distanza fra i centri (d)
0
d > r1 + r2
tangenti esternamente
1
d ≅ r1 + r2
secanti
2
r1 – r2 < d < r1 + r2
tangenti internamente
1
d ≅ r1 – r2
interne
0
d < r1 – r2
concentriche
0
d =0
34
6.7 Angoli alla circonferenza e corrispondenti angoli al centro
Vale il seguente:
TEOREMA
Ogni angolo alla circonferenza è congruente alla metà dell’angolo al centro che insiste sullo
stesso arco.
Esaminiamo i casi che si possono presentare:
1° caso: i lati dell’angolo alla circonferenza sono entrambi secanti ed il centro appartiene ad uno di
essi.
V
Γ circonferenza di centro O
.
Hp.:
O
A
AVB angolo alla circonferenza
O ∈ VB
Th.:
Γ
AVB ≅
1
AOB
2
B
Dimostrazione
Indichiamo l’angolo alla circonferenza AVB con α e l’angolo al centro corrispondente AOB con β
(fig. 57):
V
α
.
O
β
A
Γ
B
fig. 57
Dobbiamo quindi dimostrare che α ≅
1
β.
2
Osserviamo, a tale scopo, che il triangolo OAV è isoscele sulla base AV perché:
OA ≅ OV
raggi della stessa circonferenza.
Segue che:
OAV ≅ OVA
perché angoli alla base di un triangolo isoscele (“indicare OAV con α”)
[fig. 58]:
35
V
α
.
α
O
β
A
Γ
fig. 58
B
Inoltre:
AOB ≅ OAV + OVA
perché AOB è un angolo esterno al triangolo OAV ed è quindi
congruente alla somma degli angoli interni non adiacenti ad esso
(secondo teorema dell’angolo esterno, unità 3, pag. 125)
e quindi:
β≅ α + α ≅ 2 α
cioè:
α≅
1
β.
2
C.V.D.
2° caso: i lati dell’angolo alla circonferenza sono uno secante, passante per il centro, e l’altro
tangente.
V
A
Γ circonferenza di centro O
Hp.:
.
AV tangente alla circonferenza
AVB angolo alla circonferenza
O
O ∈ VB
Γ
Th.:
AVB ≅
1
VOB
2
B
Dimostrazione
Basta osservare che l’angolo alla circonferenza AVB è retto e che l’angolo al centro corrispondente
VOB è piatto, per cui:
AVB ≅
1
VOB .
2
C.V.D.
36
3° caso: i lati dell’angolo alla circonferenza sono entrambi secanti e il centro della circonferenza è
interno all’angolo.
V
Γ circonferenza di centro O
Hp.:
O.
O ∉ VA ; O ∉ VB
Γ
B
A
AVB angolo alla circonferenza
Th.:
AVB ≅
1
AOB
2
Dimostrazione
Tracciamo il diametro VC (fig. 59):
V
O.
Γ
B
A
C
fig. 59
e osserviamo che:
AVC ≅
1
AOC (1° caso)
2
BVC ≅
1
BOC (1° caso)
2
e quindi, sommando membro a membro:
AVC + BVC ≅
1
1
AOC + BOC
2
2
cioè:
AVB ≅
1
1
(AOC + BOC) ≅ AOB
2
2
C.V.D.
37
4° caso: i lati dell’angolo alla circonferenza sono uno secante e l’altro tangente; il centro della
circonferenza è interno all’angolo.
V
A
Γ circonferenza di centro O
Hp.:
.O
Γ
AVB angolo alla circonferenza
O ∈ AVB
Th.:
B
AVB ≅
1
VOB (con VOB concavo)
2
Dimostrazione
Tracciamo il diametro VC (fig. 60):
V
A
.O
Γ
B
C
fig. 60
e osserviamo che:
BVC ≅
1
BOC (1° caso);
2
AVC ≅
1
VOC (2° caso),
2
e quindi, sommando membro a membro:
BVC + AVC ≅
1
1
BOC + VOC
2
2
cioè:
BVC+ AVC ≅
1
1
(BOC + VOC) ≅
VOB
2
2
C.V.D.
38
5° caso: i lati dell’angolo alla circonferenza sono entrambi secanti e il centro della circonferenza è
esterno all’angolo.
V
Γ circonferenza di centro O
.
Hp.:
O
A
AVB angolo alla circonferenza
O ∉ AVB
Th.:
Γ
B
AVB ≅
1
AOB
2
Dimostrazione
Tracciamo il diametro VC (fig. 61):
V
.
O
A
Γ
B C
fig. 61
e osserviamo che:
AVB ≅ AVC – BVC
ma:
AVC ≅
1
AOC (1° caso)
2
BVC ≅ …..
COMPLETA
……………………………………………………………………………………………………………
……………………………………………………………………………………………………………
……………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
39
6° caso: i lati dell’angolo alla circonferenza sono uno secante e l’altro tangente; il centro della
circonferenza è esterno all’angolo.
V
A
Γ circonferenza di centro O
Hp.:
AV tangente alla circonferenza
AVB angolo alla circonferenza
.O
O ∉ AVB
Γ
B
Th.:
AVB ≅
1
VOB
2
Dimostrazione
PROVA TU
(suggerimento: traccia il diametro VC …………………)
Come conseguenze del teorema sugli angoli al centro e alla circonferenza si hanno i seguenti:
COROLLARIO 1
Angoli alla circonferenza che insistono sullo stesso arco o su archi congruenti sono congruenti.
V
C
D
O
.
A
Γ
B
Dimostrazione
PROVA TU
(suggerimento: “confronta” ogni angolo alla circonferenza con il corrispondente angolo al centro).
Vale anche il viceversa:
Angoli alla circonferenza congruenti insistono su archi congruenti (PROVA TU).
40
COROLLARIO 2
Ogni angolo alla circonferenza che insiste su di una semicirconferenza è retto.
C
A
D
.
B
O
Dimostrazione
PROVA TU
Il COROLLARIO 2 può essere formulato nel seguente modo: “ogni triangolo inscritto in una
semicirconferenza è rettangolo”.
CURIOSITÀ
Il COROLLARIO 2 è detto anche “teorema di Dante” in quanto Dante Alighieri, nel Paradiso, al
canto XIII versi 101 – 102, riporta:
“o se del mezzo cerchio far si puote
triangol sì ch’un retto non avesse”
(commento: … o se in un semicerchio si possa inscrivere un triangolo che non sia rettangolo).
VICEVERSA:
Un triangolo rettangolo si può inscrivere in una circonferenza con il diametro coincidente con
C
l’ipotenusa.
Infatti, dato un triangolo rettangolo ABC, retto in C
(figura a lato), tracciamo la circonferenza passante
A
B
per i punti A, B, C (che ….………. ed è .….….…).
CONTINUA …………………………………………………………………………………………..
…………………………………………………………………………………………………………
Il COROLLARIO 2 permette di disegnare “correttamente” un triangolo rettangolo se si ha un
compasso e un righello.
Infatti ……….. CONTINUA …………………………………………………………………………
41
1° Problema risolto
Data la circonferenza Γ di centro O e raggio r, siano AB e CD due suoi diametri. Dimostra che il
quadrilatero ACBD è un rettangolo.
A
D
.
Γ circonferenza di centro O
Hp.:
O
C
CD diametro
Th.:
Γ
AB diametro
ACBD rettangolo
B
Dimostrazione
Per il COROLLARIO 2, pag. 39, si ha che:
•
il triangolo DAC è retto in A, perché inscritto nella semicirconferenza di diametro CD;
•
il triangolo ACB è retto in C, perché inscritto nella semicirconferenza di diametro AB;
•
il triangolo CBD è retto in B, perché inscritto nella semicirconferenza di diametro CD;
•
il triangolo BDA è retto in D, perché inscritto nella semicirconferenza di diametro AB.
Pertanto il quadrilatero ACBD, avendo tutti e quattro gli angoli retti, è un rettangolo.
C.V.D.
“Quando” il rettangolo ACBD “diventa” un quadrato?
[Ti aiuto con la figura che segue:
A
D
.
O
C
Γ
B
dove AB e CD ……………. CONTINUA]
42
6.8 Tangenti condotte da un punto ad una circonferenza
Siano dati nel piano una circonferenza Γ e un punto P.
Distinguiamo i seguenti casi:
1° caso: il punto P è interno alla circonferenza (fig. 62):
.P
Γ
fig. 62
Tutte le rette passanti per P (fascio di rette di centro P) sono secanti la circonferenza e quindi non
esiste alcuna retta tangente alla circonferenza passante per P.
2° caso: il punto P appartiene alla circonferenza (fig. 63):
.P
.
O
Γ
fig. 63
In tal caso esiste una ed una sola retta t tangente alla circonferenza passante per P (punto 2. pag. 24).
Tale retta è perpendicolare al raggio OP (fig. 64):
.P
.
t
O
Γ
fig. 64
43
3° caso: il punto P è esterno alla circonferenza (fig. 65):
.
.
O
P
Γ
fig. 65
In tal caso esistono due rette t1 e t2 tangenti a Γ, passanti per P. Tracciamo, infatti, la circonferenza di
diametro OP che è secante Γ in due punti T1 e T2 (fig. 66):
T1
.
Non conduciamo … per ora
le tangenti t1 e t2 .
O
.
Γ
.
.
P
.
T2
fig. 66
Basta, poi, osservare che i due triangoli OT1P e OT2P sono retti rispettivamente in T1 e in T2 in quanto
inscritti in una semicirconferenza e quindi le rette PT1 e PT2, perpendicolari rispettivamente ai raggi
OT1 e OT2, sono le tangenti t1 e t2 a Γ, passanti per P (fig. 67):
t1
T1
.
t1 e t2 rette tangenti a Γ passanti per P.
O
.
Γ
.
.
P
I segmenti PT1 e PT2 sono detti segmenti
di tangenza.
.
t2
T2
fig. 67
44
Si ha il seguente
TEOREMA
Se da un punto P, esterno ad una circonferenza di centro O, si conducono le due rette tangenti
ad essa, i segmenti di tangenza sono congruenti.
t1
T1
.
O
Γ circonferenza di centro O
Hp.:
.
.
PT1 ⊥ OT1
P
.
Γ
t2
P∉Γ
PT2 ⊥ OT2
Th.:
PT1 ≅ PT2
T2
Dimostrazione
Congiugiamo O con P (fig. 68):
t1
T1
.
O
.
.
P
.
Γ
t2
T2
fig. 68
e consideriamo i triangoli OPT1 e OPT2; essi hanno:
OT1P ≅ OT2P
perché entrambi retti;
OP
(o OP ≅ OP per la proprietà riflessiva della congruenza);
in comune
OT1 ≅ OT2
perché raggi della stessa circonferenza.
I due triangoli, oltre all’angolo retto, hanno due altri elementi ordinatamente congruenti (che non sono
i due angoli acuti) e quindi sono congruenti per il criterio di congruenza dei triangoli rettangoli.
Avranno, pertanto, tutti gli elementi corrispondenti congruenti, in particolare:
PT1 ≅ PT2.
C.V.D.
45
COROLLARIO 1
Data una circonferenza di centro O ed un punto P esterno ad essa, il segmento PO appartiene
alla bisettrice dell’angolo formato dalle due tangenti condotte dal punto P (PROVA TU).
COROLLARIO 2
Data una circonferenza di centro O ed un punto P esterno ad essa, il segmento PO appartiene
all’asse della corda che ha per estremi i punti di tangenza (PROVA TU).
Costruzioni geometriche (con squadra e compasso)
Data una retta t , sia O un punto non appartenente a tale retta . PROVA TU a “costruire” la
circonferenza di centro O e tangente aalla retta t .
Motiva la costruzione effettuata.
Data una retta t, PROVA TU a “costruire” la circonferenza tangente a t in un punto T e
passante per un dato punto A, distinto da T.
Motiva la costruzione effettuata.
Cosa succede se il punto A appartiene alla retta t ?
Date due rette s e t, PROVA TU a “costruire” la circonferenza tangente alle due rette,
conoscendo il punto T di tangenza con una di esse.
Esegui la costruzione nei seguenti casi:
a) le rette s e t sono parallele;
b) le rette s e t sono incidenti.
Motiva le costruzioni effettuate.
(suggerimento: nel caso a), manda la mediana della striscia individuata dalle rette ….. ;
nel caso b), manda le bisettrici degli angoli formati dalle rette ….. )
Date tre rette s , t , u , a due a due incidenti, PROVA TU a “costruire” la circonferenza
tangente alle tre rette.
Motiva la costruzione effettuata.
46
2° Problema risolto
Data una circonferenza Γ di centro O, sia AB un suo diametro. Traccia le rette tangenti, t1 e t2,
rispettivamente in A e in B. Conduci, poi, un’ulteriore retta t3, tangente a Γ, tale che:
t3 ∩ Γ = {C} ;
t3 ∩ t1 = {P} ;
t3 ∩ t2 = {Q} .
Dimostra che: PQ ≅ PA + QB.
.
Q
Γ circonferenza di centro O
O ∈ AB
C
.
t1, t2, t3 tangenti a Γ
P.
Hp.:
t3
.
.
A
t3 ∩ t1 = {P}
.
O
t3 ∩ Γ = {C}
B
t3 ∩ t2 = {Q}
Th.:
Γ
PQ ≅ PA + QB
t2
t1
Dimostrazione
Osserviamo innanzitutto che la retta tangente ad una circonferenza ed il raggio passante per il punto di
tangenza sono fra loro perpendicolari per cui la figura può essere subito “arricchita” come segue:
.
Q
C
.
P.
t3
.
.
A
O
“arricchimento” eseguito
.
B
…. per non dimenticare
Γ
t1
t2
47
Inoltre:
PA ≅ PC
perchè segmenti di tangenti condotte da P (punto esterno) alla circonferenza Γ ;
QB ≅ QC
perchè segmenti di tangenti condotte da Q (punto esterno) alla circonferenza Γ .
Pertanto, da:
PQ ≅ PC + QC
segue:
PQ ≅ PA + QB.
C.V.D.
48
ESERCIZI UNITÀ 6
Conoscenza e comprensione
1) Definisci la circonferenza.
2) Definisci il cerchio.
3) Le seguenti proposizioni sono vere o false?
a) La circonferenza è un sottoinsieme del cerchio.
V
F
b) Una corda è una linea che unisce due punti di una circonferenza.
V
F
c) Il diametro di una circonferenza è una corda.
V
F
d) Una corda è un segmento che ha per estremi due punti del cerchio.
V
F
e) Una corda è anche un diametro di una circonferenza.
V
F
f) Una corda è un segmento che ha per estremi due punti di una circonferenza. V
F
g) Un segmento passante per il centro di una circonferenza è un diametro.
V
F
h) Due circonferenze sono congruenti se hanno lo stesso raggio.
V
F
i) Due cerchi sono congruenti se hanno i raggi congruenti.
V
F
4) In una circonferenza, due punti sono diametralmente opposti se:
a) appartengono alla circonferenza;
b) hanno la stessa distanza dal centro;
c) sono gli estremi di un diametro;
d) sono gli estremi di una corda.
5) Completa le seguenti proposizioni in modo che risultino vere:
a) un punto è ……………….. alla circonferenza se la sua distanza dal centro è minore del
raggio;
b) un punto è esterno alla circonferenza se la sua distanza dal centro è ………………..... del
raggio;
c) un punto …………………….. alla circonferenza se la sua distanza dal centro è congruente
al raggio.
49
6) Quanti e quali sono gli assi di simmetria di una circonferenza? Spiega perché.
7) Quanti e quali sono i centri di simmetria di una circonferenza? Spiega perché.
8) Rispetto a quale trasformazione la circonferenza è una figura unita?
9) Che cosa si intende per arco di una circonferenza?
10) In quale caso un arco di circonferenza prende il nome di semicirconferenza?
11) Un settore circolare è l’intersezione di due insiemi di punti. Quali?
12) Un segmento circolare è l’intersezione di due insiemi di punti. Quali?
13) Che cosa si intende per altezza di un segmento circolare a due basi? E per altezza di un
segmento circolare ad una base?
14) Dai la definizione di angolo al centro e angolo alla circonferenza.
15) Cosa vuol dire che un angolo al centro o alla circonferenza insiste sull’arco AB?
16) In quale caso un angolo alla circonferenza e un angolo al centro si dicono corrispondenti?
17) Una sola delle seguenti proposizioni è vera. Quale?
La relazione che ad ogni angolo alla circonferenza associa il corrispondente angolo al centro:
a) è una funzione iniettiva;
b) è una funzione suriettiva;
c) è una funzione invertibile;
d) è una funzione;
e) non è una funzione.
18) La misura di una corda di una circonferenza, espressa in cm, è 25. Quale, fra i seguenti numeri,
può esprimere la misura, in cm, del raggio della circonferenza?
a) 10;
b) 13;
c) 8;
d) 12;
e) 3;
f) 28;
g) 9;
h) 12,5.
19) Una circonferenza ha il raggio di 8 cm. Quali delle seguente lunghezze, espresse in cm, possono
rappresentare corde della circonferenza? Motiva la tua risposta:
a) 7;
b) 10;
c) 18;
d) 2,7;
e) 16;
f) 20;
g) 0,3;
h) 9;
50
i) 8,2;
l) 12;
m) 15;
n) 16,1.
20) Vero o falso?
a) La distanza di una corda dal centro può essere maggiore del raggio della
V
F
b) Il centro di una circonferenza appartiene all’asse di una sua corda.
V
F
c) Il punto medio di una corda di una circonferenza appartiene alla perpendicolare
V
F
d) Se due corde hanno la stessa distanza dal centro, le due corde sono congruenti.
V
F
e) Due corde di una circonferenza tra loro parallele, hanno la stessa distanza dal
V
F
V
F
circonferenza.
alla corda passante per il centro della circonferenza.
centro della circonferenza.
f) La distanza di una corda dal centro è sempre minore del raggio della
circonferenza.
21) AB e CD sono due corde di una stessa circonferenza tali che AB > CD. Quale relazione esiste
fra le loro distanze dal centro della circonferenza?
22) Una sola delle seguenti proposizioni è vera. Quale?
a) Per tre punti distinti del piano passa una sola circonferenza.
b) Le circonferenze passanti per due punti del piano sono più di una, ma in numero finito.
c) Siano A e B due punti distinti del piano; i centri di tutte le circonferenze passanti per A e B
non sono allineati.
d) Se i centri di due circonferenze distinte appartengono all’asse del segmento AB, le due
circonferenze passano per gli estremi del segmento.
e) Tre punti di una circonferenza possono essere allineati.
23) Quando una retta è esterna ad una circonferenza? E quando è tangente? E quando è secante una
circonferenza?
24) Sia s una retta secante una circonferenza il cui raggio misura 5 cm. Quali, fra i seguenti numeri
può rappresentare la distanza, espressa in cm, di s dal centro della circonferenza?
a) 9;
b) 5;
c) 4,8;
d) 7;
e) 6.
51
25) Siano Γ una circonferenza di raggio r e v una retta. Se esiste almeno un punto di v la cui distanza
dal centro di Γ è minore di r, che cosa si può dire della posizione di v rispetto a Γ?
26) Siano Γ una circonferenza di raggio r ed a una retta. Se esiste almeno un punto di a la cui
distanza dal centro di Γ è maggiore di r, che cosa si può dire della posizione di a rispetto a Γ?
27) Siano Γ una circonferenza di raggio r e b una retta. Se esiste almeno un punto di b la cui
distanza dal centro di Γ è congruente ad r, che cosa si può dire della posizione di b rispetto a Γ?
28) Siano Γ una circonferenza di raggio r e d una retta. Se esiste un solo punto di d la cui distanza
dal centro di Γ è congruente ad r, che cosa si può dire della posizione di d rispetto a Γ?
29) Quante e quali posizioni possono assumere, reciprocamente, due circonferenze?
30) Una sola delle seguenti proposizioni è vera. Quale?
Se due circonferenze non hanno punti in comune, allora:
a) sono sicuramente una esterna all’altra;
b) sono tangenti;
c) sono sicuramente una interna all’altra;
d) nessuna delle precedenti affermazioni è corretta.
31) Siano Γ1 e Γ2 due circonferenze di centro, rispettivamente, O1 e O2 e di raggio, rispettivamente,
r1 e r2 (r1 > r2). Completa le seguenti proposizioni in modo che esse risultino vere:
a) se r1 + r2 < O1O2,
Γ1 e Γ2 sono ………………. ;
b) se r1 + r2 ….. O1O2,
Γ1 e Γ2 sono tangenti esternamente;
c) se r1 − r2 < O1O2 < r1 + r2, Γ1 e Γ2 sono ………………. ;
d) se r1 − r2 ≅ O1O2,
Γ1 e Γ2 sono ………………………………….. ;
e) se r1 − r2 > O1O2,
Γ1 e Γ2 sono ………………………………….. .
32) Siano A, B e V punti della circonferenza Γ di centro O, allora:
a) AOB è la metà di AVB;
b) AVB è il doppio di AOB;
c) AOB è il doppio di AVB;
d) AOB ≅ AVB;
52
e) AOB < AVB.
33) Che cosa si intende per corona circolare?
34) Perché angoli alla circonferenza che insistono sullo stesso arco o su archi congruenti sono
congruenti?
35) Sia AB il diametro di una circonferenza Γ e P un punto di Γ. Una sola delle seguenti
affermazioni è corretta. Quale?
a) APB è acuto;
b) APB è ottuso;
c) APB è retto.
36) Stabilisci se le seguenti proposizioni sono vere o false:
a) Un triangolo inscritto in una circonferenza può essere rettangolo.
V
F
b) Un triangolo inscritto in una semicirconferenza è sempre un triangolo
V
F
V
F
V
F
rettangolo.
c) Se il centro di una circonferenza non è interno ad un triangolo inscritto
in essa, il triangolo è sicuramente ottusangolo.
d) Se un triangolo inscritto in una circonferenza è acutangolo, allora il centro
della circonferenza è interno al triangolo
37) Sia P un punto del piano esterno ad una circonferenza Γ; quante sono le rette tangenti a Γ che
passano per P?
38) Che cosa si intende per segmento di tangenza o di tangente?
39) Una sola delle seguenti proposizioni è vera. Quale?
Se per un punto P del piano non passa alcuna retta tangente alla circonferenza Γ, allora:
a) P è esterno a Γ;
b) P è interno a Γ;
c) P è un punto di Γ.
40) Sia P un punto della circonferenza Γ di centro O e s una retta tangente a Γ passante per P; quale
delle seguenti affermazioni è corretta?:
53
a) l’angolo che OP forma con la retta s è ottuso;
b) l’angolo che OP forma con la retta s è acuto;
c) l’angolo che OP forma con la retta s è retto.
41) Le proposizioni che seguono si riferiscono alla seguente figura. Stabilisci se sono vere o false:
t1
H
.
P.
.
O..
D.
t1 e t2 tangenti per P alla circonferenza
.
K
t2
a) POH e OPK sono complementari.
V
F
b) Il triangolo HPK è isoscele.
V
F
c) HDK e HOP sono complementari.
V
F
d) HOK e HPK sono supplementari.
V
F
e) HK è perpendicolare ad OP.
V
F
f) HDK e HPK sono supplementari.
V
F
g) KHO ≅ HPO.
V
F
h) POK ≅ PKH.
V
F
i) HDK ≅ 2 HOK.
V
F
j) t1 ∩ t2 = {H, K).
V
F
k) Il triangolo HOK è equilatero.
V
F
l) DH è perpendicolare a t1
V
F
V
F
m) DH < 2 OH
54
Motiva le risposte.
42) In base alla seguente figura:
D
H
C
.
A
O
B
Γ
t
completa le varie affermazioni:
1.
O è il ……………………………………………………….………….;
2.
AB è il . ……………………………………………………………….;
3.
AO è ……………………………………………………….………….;
4.
CD è …………………………………………………………………..;
5.
OH è ……………………………………………………….………….;
6.
H è ...……...……………………………………………… …………..;
7.
t è ...…………………………………………………………………. .
43) Stabilisci se le seguenti proposizioni sono vere o false:
a) Un angolo che ha per vertice un punto della circonferenza è un
V
F
b) Due circonferenze che non hanno punti in comune sono esterne.
V
F
c) Due circonferenze secanti hanno tre tangenti comuni.
V
F
d) Due circonferenze esterne non hanno tangenti comuni.
V
F
e) Due circonferenze concentriche possono avere centri diversi.
V
F
f) Un angolo che ha per vertice un punto della circonferenza è un
V
F
angolo alla circonferenza.
55
angolo al centro.
g)
Da un punto appartenente ad una circonferenza si possono condurre
V
F
più di una tangente alla circonferenza stessa.
Applicazione
1) Riferendoti alla seguente figura, misura con la squadra le lunghezze dei segmenti indicati e
completa:
.B
OA ≅ …. cm.
.
A
O
OB ≅ ….cm
OA…. OB (inserisci uno dei simboli < , > , ≅ )
2) Che cosa rappresenta la seguente figura?
B
O
A
Riproduci la figura sul tuo quaderno e, senza far uso del goniometro, valuta, approssimativamente,
l’ampiezza dell’angolo convesso AOB.
3) Disegna una circonferenza di raggio qualsiasi e traccia le rette q, s, t, tra loro parallele, tali che:
q sia esterna alla circonferenza;
s sia secante la circonferenza;
t sia tangente alla circonferenza.
4) Riproduci sul quaderno l’angolo AOB della figura a lato.
A
Traccia la sua bisettrice b e prendi su di essa un
punto P, distante 5 cm dal vertice O. Conduci, poi, i
segmenti PH e PK, perpendicolari rispettivamente ai lati
OA e OB. Traccia, infine, la circonferenza di centro P
56
tangente ai lati dell’angolo dato.
Qual è il raggio di tale circonferenza?
O
B
5) Traccia la distanza OH della retta q dal centro O della circonferenza Γ di raggio r e completa le
relazioni riportate:
q ∩ Γ = ….
.O
OH …. r
Γ
q
6) Traccia la distanza OH della retta s dal centro O della circonferenza Γ di raggio r e completa le
relazioni riportate:
Γ
s ∩ Γ = ….
.O
OH …. r
.
A
.
B
s
7) Traccia la distanza OH della retta t dal centro O della circonferenza Γ di raggio r e completa le
relazioni riportate:
t
Γ
t ∩ Γ = ….
.
O
.
Come si chiama questo punto?
Perché?
57
Dopo aver disegnato una circonferenza Γ di centro O e raggio r = 4 cm , risolvi i seguenti esercizi:
8) Traccia una circonferenza Γ1 di centro O1 , distante da O di un segmento congruente a 3 cm, e
raggio r1 = 2 cm .
Come risultano Γ e Γ1 ?
9) Traccia una circonferenza Γ2 di centro O2 , distante da O di un segmento congruente a 3 cm, e
raggio r2 = 1 cm .
Come risultano Γ e Γ2 ?
10) Traccia una circonferenza Γ3 di centro O3 , distante da O di un segmento congruente a 5 cm, e
raggio r3 = 1 cm .
Come risultano Γ e Γ3 ?
11) Traccia una circonferenza Γ4 di centro O4 , distante da O di un segmento congruente a 2 cm, e
raggio r4 = 1 cm .
Come risultano Γ e Γ4 ?
12) Traccia una circonferenza Γ5 di centro O5 ≡ O e raggio r5 = 3 cm..
Come risultano Γ e Γ5 ?
13) Traccia una circonferenza Γ6 di centro O6 , distante da O di un segmento congruente a 8 cm, e
raggio r6 = 3 cm .
Come risultano Γ e Γ6 ?
Come deve variare r6 affinchè le circonferenze Γ e Γ6 mantengano la stessa posizione
reciproca?
14) Nella figura a lato è rappresentato il segmento OB ≅ OA + AB.
Riproduci sul tuo quaderno tale segmento e disegna la figura che si ottiene
.
facendo compiere al segmento OB una rotazione completa intorno ad O.
B
A
I punti A e B cosa descrivono?
E il segmento OB?
.
O
.
E il segmento OA?
58
E il segmento AB?
In ognuno dei seguenti esercizi è rappresentato un angolo alla circonferenza α. Disegna l’angolo al
centro corrispondente β e, data la misura di α, determina quella di β.
15)
A
α
.
α = 21° 8'
β = …….. = ………
O
B
C
16)
D
α
.
F
O
α = 74° 30'
β = …….. = ………
E
17)
L
α
α = 31° 30'
.
O
β = …….. = ………
M
N
59
18) Completa la seguente tabella sapendo che AVB è un angolo alla circonferenza e AOB è il
corrispondente angolo al centro:
AVB
24°
45°
AOB
20°
140°
68°
76°
44°
52°
Disegna, poi, una figura per ciascuna coppia di angoli corrispondenti.
Calcola l’ampiezza degli angoli indicati con i simboli x, y, … .
19)
C
.
x
48°
B
O
A
20)
C
.O
x
A
D
18°
B
21)
C
x
O.
D
y
42°
44°
A
B
60
22)
P
y 20°
O.
Q
S
36° x
R
23)
U
x
O.
T
40°
R
65°
S
24)
V
z
B
x
O.
t tangente in B alla circonferenza
20°
t
y
A
25)
.
A
x
t1 tangente in A alla circonferenza
O 28°
B
t2 tangente in B alla circonferenza
y
61
t1
C
t2
26) La somma di due angoli alla circonferenza è 114°. Sapendo che uno è i 9/10 dell’altro, qual è
l’ampiezza dei corrispondenti angoli al centro?
[108° ; 120°]
27) La somma di due angoli alla circonferenza è 96°. Sapendo che uno è triplo dell’altro, qual è
l’ampiezza dei corrispondenti angoli al centro?
[144° ; 48°]
28) La somma di due angoli alla circonferenza è 105° e la loro differenza è 47°. Qual è l’ampiezza dei
corrispondenti angoli al centro?
[152° ; 58°]
29) Qual è l’ampiezza degli angoli alla circonferenza che insistono rispettivamente su archi che sono
2 3 1 2 5
,
,
,
,
della circonferenza?
5 8 6 3 8
[108° ; ………]
30) Due angoli al centro hanno come somma 165° e sono uno i
2
dell’altro. Qual è l’ampiezza dei
3
corrispondenti angoli alla circonferenza?
[33° ; 49°30’]
31) Dividi un cerchio in tre settori circolari in modo che l’ampiezza del secondo sia
2
di quella del
5
primo e che l’ampiezza del terzo sia la metà di quella del secondo. Qual è l’ampiezza di ogni
settore?
[225° ; 90° ; 45°]
32) Dividi un cerchio in tre settori circolari in modo che il secondo abbia ampiezza doppia di quella del
primo e il terzo ampiezza pari alla somma dei primi due. Qual è l’ampiezza di ogni settore?
[60° ; 120° ; 180°]
62
33)
Dividi un cerchio in tre settori circolari in modo che le ampiezze del secondo e del terzo siano
rispettivamente
1
3
e
di quella del primo. Qual è l’ampiezza di ogni settore?
5
5
[200° ; 40°; 120°]
Problemi
Corde e archi
1) Siano date una circonferenza Γ, di centro O, e due sue corde AB e CD tra loro congruenti. Detto P
il punto di intersezione delle rette contenenti le due corde, dimostra che la congiungente PO è
bisettrice dell’angolo BPD.
2) In una circonferenza di centro O è data una corda AB la cui distanza dal centro è congruente alla
metà della corda stessa. Considerata la simmetria σs , di asse la retta s , contenente il diametro
parallelo ad AB, sia:
σs (A) = A' ;
σs (B) = B' .
Dimostra che gli archi AB, BB', B'A' e A'A sono congruenti.
3) Siano date una circonferenza Γ e due corde parallele AB e CD. Dimostra che se AB ≅ CD (figura
.D
a lato) allora il quadrilatero ABDC è un rettangolo.
C.
.
O
.B
.
A
4) Siano date una circonferenza Γ e due corde parallele AB e CD. Dimostra che se AB ≅ CD (nella
figura a lato AB > CD) allora il quadrilatero ABDC è un trapezio isoscele.
.D
C.
.
.B
O
.
A
63
5) Siano dati una circonferenza Γ, di centro O, e una sua corda AB. Considera su AB due punti C e D
tali che AC ≅ BD. Dimostra che il triangolo COD è isoscele.
6) Data una circonferenza Γ di centro O, sia OA un suo raggio. Dopo aver tracciato una corda BC
parallela ad OA (figura a lato), dimostra che il segmento BA biseca l’angolo CBO.
.C
.A
B.
.
O
7) Sia AB una corda di una circonferenza di centro O. Considerata la simmetria σs ,di asse la retta s ,
contenente il diametro CD, parallelo ad AB, sia:
σs (A) = A' ;
σs (B) = B' .
Dimostra che i triangoli ACA' e BDB' sono congruenti.
8) Siano dati una circonferenza di centro O e un suo diametro AB. Condotte le corde AC e BD,
parallele tra loro, dimostra che AC ≅ BD.
9)
Siano dati una circonferenza Γ, di centro O, ed una sua corda AB. Dopo aver prolungato la corda
di due segmenti congruenti AC e BD, dimostra che OC ≅ OD.
10) Data una circonferenza Γ, conduci due suoi diametri AB e CD. Dimostra che il quadrilatero
ADBC è un rettangolo.
11) Data una circonferenza Γ, conduci due suoi diametri AB e CD tra loro perpendicolari. Dimostra
che il quadrilatero ADBC è un quadrato.
12) In una circonferenza Γ, di centro O, considera due corde AB e CD, incidenti perpendicolarmente
nel punto E. Conduci da O le perpendicolari alle corde AB e CD ed indica con H e K i rispettivi
piedi delle perpendicolari.
64
Dimostra che il quadrilatero OHEK è un rettangolo.
Quando il quadrilatero OHEK è un quadrato?
13) Siano date una circonferenza Γ di centro O e una sua corda AB. Prolunga la corda di due segmenti
AC e BD congruenti fra loro. Dimostra che i triangoli AOD e BOC sono congruenti.
14) Sia data una circonferenza Γ di centro O e due sue corde AB e CD congruenti. Prolunga le due
corde di due segmenti BE e DF congruenti fra loro (figura a lato):
.B //
E.
*
A.
.O
C.
*
Γ
.
D //
.
F
Dimostra che il segmento EF ha per asse una retta diametrale.
(suggerimento: manda dal centro O le perpendicolari alle corde e considera i due triangoli
……….. )
Reciproche posizioni fra retta e circonferenza
Reciproche posizioni fra due circonferenze
15) Data una circonferenza Γ di centro O, sia s una retta secante Γ nei punti P e Q. Traccia un
diametro AB ed indica con H e K le proiezioni ortogonali rispettivamente di A e B sulla retta s.
Dimostra che OH ≅ OK.
16) Data una circonferenza Γ di centro O, sia s una retta secante Γ nei punti P e Q. Traccia un
diametro AB ed indica con H e K le proiezioni ortogonali rispettivamente di A e B sulla retta s.
Dimostra che HC ≅ DK.
17) Siano date due circonferenze concentriche Γ e Γ', di centro O e raggi rispettivamente r ed r', con
r < r'. Considera una retta s tale che:
65
s ∩ Γ = {A, B};
s ∩ Γ' = {C, D}.
Dimostra che i segmenti CA e BD , compresi fra le due circonferenze, sono congruenti.
18) Siano date due circonferenze concentriche Γ e Γ' di centro O e raggi rispettivamente r ed r', con
r < r'. Dimostra che:
1. due qualsiasi corde della circonferenza maggiore, tangenti a quella minore, sono congruenti;
2. il punto di tangenza di ogni corda è il punto medio della corda stessa.
19) Data una circonferenza Γ di centro O, siano q e s due rette parallele secanti Γ. Dimostra che gli
archi compresi fra le due parallele sono congruenti.
20) Siano date due circonferenze esterne:
Γ1 di centro O1 e raggio r1,
Γ2 di centro O2 e raggio r2,
con r1 ≠ r2.
Conduci le tangenti esterne s e t, comuni alle due circonferenze, e dimostra che tali tangenti si
incontrano sulla retta dei centri O1 e O2 (fig. a lato):
A
.
Γ1
B
.
.
.
O1
O2
.
D
.
s
Γ2
t
C
(suggerimento: la bisettrice di un angolo è il luogo dei punti …….. )
PERCHÈ abbiamo posto r1 ≠ r2?
21) Due circonferenze Γ1 e Γ2 , di centri rispettivamente O1 e O2, sono tangenti esternamente in un
punto T. Conduci da T una retta s che incontri ulteriormente la circonferenza Γ1 in A e la
circonferenza Γ2 in B. Dimostra che la retta tangente in A a Γ1 è parallela alla retta tangente in B
alla Γ2.
22) Siano date due circonferenze concentriche Γ e Γ' di centro O e raggi rispettivamente r ed r', con
r < r'. Siano:
66
AB un diametro della circonferenza Γ' ;
CD un diametro della circonferenza Γ, non contenuto in AB.
Dimostra che il quadrilatero ACBD è un parallelogramma.
Angoli al centro e angoli alla circonferenza
Tangenti a una circonferenza
24)
Sia dato il triangolo ABC, retto in C. Detto M il punto medio di AB, dimostra che:
1) BAC ≅
1
BMC;
2
2) ABC ≅
1
AMC.
2
25) Data una circonferenza Γ, sia BAC un suo angolo alla circonferenza. Detta AM la mediana
dell’arco sotteso dall’angolo BAC, conduci la corda CD parallela ad AM.
Dimostra che AD ≅ BM.
26)
Sia data una semicirconferenza di diametro AB. Conduci da B la retta t tangente alla
semicirconferenza e prendi su di essa un punto P tale che BP ≅ AB. Dimostra che il segmento AP
incontra la semicirconferenza nel suo punto medio M.
(suggerimento: angoli alla circonferenza …….. )
27)
Siano date una circonferenza Γ, di centro O, ed una sua corda AB. Conduci la tangente t in B a Γ e
prendi su di essa, nel semipiano individuato dalla retta AB contenente O, un punto C tale che CB
sia congruente alla corda AB.
Se:
AC ∩ Γ = {P},
dimostra che:
1) PB ≅ PC ;
2) BPC ≅ 2 .OBP .
28) Sia data una circonferenza Γ di centro O. Da un punto P, esterno a Γ, conduci una delle due tangenti
e dal punto di tangenza T manda la perpendicolare al segmento OP, indicando con H il piede di
tale perpendicolare.
Se :
67
Γ ∩ OP = {A},
dimostra che TA è bisettrice dell’angolo PTH.
29)
Siano date due circonferenze esterne Γ1 e Γ2 , di centri rispettivamente O1 e O2. Traccia due rette,
t1 e t2, tangenti comuni a Γ1 e Γ2 (figura a lato). Dimostra che i segmenti AB e CD sono
congruenti.
.A
.
D
.
.
O1
P
.
C
t2
.
.
O2
B
t1
Che cosa puoi dire del quadrilatero ACBD?
31) Siano dati una circonferenza Γ, di centro O, e un suo diametro AB. Condotta la corda AC
congruente al raggio, prolunga AB, dalla parte di A, di un segmento AD congruente ad AC.
Dimostra che il segmento DC è tangente a Γ.
32) Data una circonferenza Γ di centro O, siano AB e AC rispettivamente un diametro ed una corda.
Dai punti A e C manda le tangenti t1 e t2 a Γ. Dimostra che t1t2 ≅ 2 BAC.
33) Siano dati una circonferenza Γ, di centro O, e due corde congruenti AB e BC. Condotte dagli
estremi A, B, C rispettivamente le tangenti t1, t2, t3 a Γ e indicati con:
{D} = t1 ∩ t2 ;
{E} = t2 ∩ t3 ,
dimostra che i triangoli ABD e BCE sono congruenti.
34) Sia data una circonferenza Γ di centro O. Considera un arco AB e la corda ad esso sottesa. Detto M
il punto medio dell’arco AB, dimostra che la tangente in M a Γ è parallela alla corda AB.
“Scrivi” e “dimostra” la proposizione inversa.
(suggerimento: “se una corda e una tangente sono ………. )
68
35) Siano date due circonferenze Γ1 e Γ2 , tangenti internamente nel punto T, con Γ1 di raggio
maggiore a quello di Γ2. Dal punto A del diametro AT di Γ1 conduci le tangenti a Γ2 , indicando
con B e C i punti di intersezione con la tangente comune t.
Dimostra che il triangolo ABC è isoscele.
36) Nella figura a lato sono date due circonferenze Γ1 e Γ2 , di centri rispettivamente O1 e O2, tangenti
esternamente nel punto A.
Sapendo che le rette s, t, u sono le tangenti
comuni a Γ1 e a Γ2 e che:
u
.B
Γ1
s ∩ u = {F} ;
.
t ∩ u = {G},
.
.
1. F è il punto medio del segmento BC;
C
.
D
s
Γ2
.
A.
O1
dimostra che:
.F
O2
.
E
G
t
2. G è il punto medio del segmento DE;
3. il triangolo ABC è retto in A.
37) Siano dati una circonferenza Γ, di centro O, e un suo diametro AB. Dimostra che le rette tangenti a
Γ, condotte dagli estremi del diametro, sono parallele.
38) Siano date due circonferenze Γ1 e Γ2 , di centri rispettivamente O1 e O2, con Γ2 interna a Γ1.
Conduci le corde AB e CD di Γ1 , tangenti a Γ2 , parallele alla retta dei centri (figura a lato):
Γ1
B
Γ2
.
A
O1
.
O2
D
C
Dimostra che AB ≅ CD.
(suggerimento: osserva che le due corde hanno distanze ……….. )
39) Siano date due circonferenze Γ e Γ' tangenti esternamente e sia T il loro punto di contatto. Traccia
da T due rette q ed s secanti le circonferenze.
Sapendo che:
q ∩ Γ = {A, T}
69
q ∩ Γ' = {B, T}
s ∩ Γ = {C, T}
s ∩ Γ' = {D, T}
dimostra che AC // BD.
Problemi di riepilogo
40) Siano Γ1 e Γ2 due circonferenze tangenti esternamente nel punto T. Conduci da T due rette r ed s
che intersecano rispettivamente la circonferenza Γ1 nei punti A e B e la circonferenza Γ2 nei punti
C e D. Dimostra che i triangoli ABT e CDT hanno gli angoli a due a due congruenti.
(suggerimento: conduci da T la tangente comune …………)
41) Sia data una circonferenza Γ di centro O. Da un punto P di Γ conduci le corde PA e PB e siano M
ed N i rispettivi punti medi. Detto Q il punto medio del raggio PO, dimostra che MQ ≅ NQ.
(suggerimento: congiungi A e B con O; il segmento che unisce i punti medi di due lati di un
triangolo …….. )
42) Siano date due circonferenze Γ1 e Γ2 , secanti tra loro nei punti A e B. Conduci da A una retta s che
incontri ulteriormente Γ1 e Γ2 rispettivamente in C e D.
Dimostra che l’angolo CBD non varia al variare della retta s.
(suggerimento: conduci per A una ulteriore retta t secante le due circonferenze; angoli alla
circonferenza che insistono sullo stesso arco ……….. )
43) Sia dato un triangolo ABC, isoscele sulla base BC, con il vertice A centro di una circonferenza Γ di
raggio maggiore di ciascuno dei lati congruenti del triangolo. Detti P e Q i punti di intersezione
della retta BC con Γ, dimostra che BP ≅ CQ.
(suggerimento: considera i triangoli ABP e …….. )
44) Siano date una circonferenza Γ di centro O e due rette t1 e t2 , tangenti a Γ, con t1 // t2 . Sia t3
un’ulteriore tangente allla circonferenza tale che:
t3 ∩ t1 = {A} ,
t3 ∩ t2 = {B} .
Dimostra che il segmento AB è visto da O secondo un angolo retto.
45) Siano date due circonferenze Γ1 e Γ2 , tangenti esternamente nel punto T. Traccia da T la tangente t
comune alle due circonferenze e, da un punto P ∈ t, conduci le ulteriori tangenti alle circonferenze.
70
Se:
{A} = t ∩ Γ1 ,
{B} = t ∩ Γ2 ,
dimostra che il triangolo PAB è isoscele.
46) Dati una circonferenza Γ di centro O ed un punto P interno a Γ, conduci per P la corda di
lunghezza minima.
(suggerimento: unisci il centro O con P e traccia la corda AB, passante per P e perpendicolare
ad OP …….. )
47) Siano date due circonfrenze Γ e Γ', di centri rispettivamente O e O’, congruenti e tangenti
esternamente nel punto T. Conduci da T, dalla stessa parte rispetto alla retta dei centri, due corde
TA e TB, perpendicolari tra loro.
Dimostra che AB // OO’.
(suggerimento: conduci da T la tangente comune alle due circonferenze; angoli alla circonferenza
e angoli al centro …………… )
48) Siano dati una circonferenza Γ e un suo diametro AB. Indicati con M il punto medio di una delle
due semicirconferenze e con P un generico punto dell’altra semicirconferenza, dimostra che la
corda PM è bisettrice dell’angolo APB.
49) Siano dati una circonferenza Γ e un suo diametro AB. Conduci la corda AC e prolungala di un
segmento CD ≅ AC.
a) Dimostra che BD ≅ BA.
b) Traccia da A la perpendicolare ad AC ed indica con E l’ulteriore punto di intersezione con la
circonferenza. Prolunga AE di un segmento EF ≅ AE. Dimostra che i punti D, B ed F sono
allineati.
(suggerimento: indica l’angolo BAC con α e “osserva” gli angoli ACB e AEB ………. )
50) Date due circonferenze secanti Γ e Γ', siano A e B i loro punti di intersezione. Condotti i diametri
AC e AD, dimostra che i punti C, B e D sono allineati.
(suggerimento: “osserva ” gli angoli ABC e ABD ……… )
51) Sia data una circonferenza Γ di centro O. Prendi un punto P su Γ e conduci da tale punto due corde
qualsiasi PA e PB. Detti M, N e Q i punti medi rispettivamente di PA, PB e PO, dimostra che
MQ ≅ NQ.
71
(suggerimento: unisci i punti A e B con il centro O della circonferenza; i segmenti che uniscono i
punti medi …………………)
52) Siano dati una circonferenza Γ di centro O e due suoi archi congruenti AB e CD. Conduci da A e
da C rispettivamente le tangenti t1 e t2 a Γ. Dimostra che la distanza di B dalla t1 è congruente a
quella di D dalla t2.
53) Relativamente alla circonferenza di centro O, rappresentata nella figura a lato,
C
si sa che le corde AC e AD formano angoli congruenti con il diametro AB.
Dimostra, utilizzando la simmetria, che:
a)
AC ≅ AD ;
.
.
A .
O
B
b) AOC ≅ AOD .
D
54) Sia dato un triangolo ABC, isoscele sulla base AB. Traccia la circonferenza di centro C, secante i
lati CA e CB rispettivamente nei punti D ed E. Dimostra che il quadrilatero ABED è un trapezio
isoscele.
72
OLIMPIADI
55) ABC è un triangolo rettangolo in B non isoscele e D l’ulteriore intersezione del cerchio di diametro
BC con l’ipotenusa. Dire quali delle seguenti affermazioni è falsa (DF è la tangente alla
circonferenza in D):
a. BFD = 2 BAC
C
.
b. DF = FA
.D
c. DF biseca l’angolo BDA
d. DF biseca il segmento BA
.
O
e. FD = FB
.
.
.
B
F
A
[Gara Senior, 1992]
56) Siano AC e BC due corde di una circonferenza aventi un estremo in comune, M' sia il punto
dell’arco AC (non contenente B) equidistante da A e da C e M'' il punto dell’arco BC (non
contenente A) equidistante da B e da C.
Se H e K sono le intersezioni del segmento M'M'' con le due corde, si dimostri che CHK è
isoscele.
[Olimpiadi della Matematica, Gara Senior, 1993]
57) Supponiamo che nel cerchio in figura l’angolo BAC sia di 35°. Se CD è il diametro passante per
C, quanto vale BCD?
B.
a. 35°
b. 45°
c. 50°
C.
35°
.
O
.A
.D
d. 55°
[Giochi di Archimede, 1998]
73
58) PR e QR sono tangenti al cerchio in figura. Sapendo che l’arco PSQ è quattro volte l’arco PTQ,
allora l’angolo PRQ è:
a. 72°
.P
b. 90°
c. 105°
S.
d. 108°
.
T.
O
.R
.
e. 120°
Q
[Giochi di Archimede, Gara del biennio 3 dicembre 1997]
59) La lunghezza del lato di un quadrato posto su un piano è di 1 cm. Ogni vertice di questo
quadrato è centro di una circonferenza di raggio 1 cm, giacente nello stesso piano. In quanti punti
del piano si intersecano queste circonferenze?
a. 6
b. 8
c. 10
d. 12
e. 14
[Kangourou Italia – Cadet 15 marzo 2001]
60) ABC è un triangolo equilatero e B è il punto medio del segmento AD (vedi figura). Un punto E è
scelto nello stesso piano in modo che DE = AB. Si sa che la distanza tra C ed E è la massima
possibile. Quanto misura l’angolo BED ?
a) 45°
C
b) 30°
c) 20°
d) 15°
A
B
D
e) 10°
[Kangourou Italia – Cadet 15 marzo 2001]
74
61) Siano A, B, C tre punti su una circonferenza di centro O. Sia D un punto esterno alla circonferenza
situato sulla retta AB dalla parte di B. Sapendo che CBD = 72°, quanto misura l’angolo AOC ?
D
B
.
A.
.
.C
.
O
a) 135°
b) 144°
c) 153°
d) 162°
e) 171°
[Olimpiadi della Matematica, Giochi di Archimede, 2004]
62) E’ data una circonferenza di diametro AB e centro O. Sia C un punto sulla circonferenza (diverso
da A e da B) e si tracci la retta r parallela ad AC passante per O. Sia D l’intersezione di r con la
circonferenza dalla parte opposta di C rispetto ad AB. Dimostrare che DO è bisettrice di CDB.
[Olimpiadi della Matematica, gara provinciale 2007]
63) Sia AB una corda di una circonferenza e P un punto interno ad AB tale che AP = 2 PB. Sia DE la
corda passante per P e perpendicolare ad AB. Dimostrare che il punto medio Q di AP è
l’ortocentro di ADE.
[Olimpiadi della Matematica, gara provinciale 2008]
64) E’ dato un triangolo ABC rettangolo in A e con AC cateto maggiore; sia M il punto medio di BC,
N il simmetrico di A rispetto a BC, O l’intersezione fra la perpendicolare ad MN passante per N e
la retta contenente BC. Dimostrare che l’angolo OMN è il doppio dell’angolo ACB.
[Olimpiadi della Matematica, gara provinciale 2009]
75
UNITÀ 7
POLIGONI INSCRITTI E CIRCOSCRITTI. POLIGONI REGOLARI
7.1 Generalità
Un poligono si dice inscritto in una circonferenza /in un cerchio se tutti i suoi vertici appartengono
alla circonferenza.
In tal caso la circonferenza /il cerchio si dice circoscritta/o al poligono.
In fig. 1 è rappresentato il pentagono ABCDE che è inscritto nella circonferenza Γ:
D
E
C
A
Γ
B
fig. 1
In fig. 2 è rappresentato il quadrilatero ABCD che non è inscritto nella circonferenza Γ:
C
PERCHÈ?
D
A
B
Γ
fig. 2
Un poligono si dice circoscritto ad una circonferenza /ad un cerchio se tutti i suoi lati sono tangenti
alla circonferenza.
In tal caso la circonferenza / il cerchio si dice inscritta/o nel poligono ed il raggio si dice apotema del
poligono.
76
In fig. 3 è rappresentato l’esagono ABCDEF che è circoscritto alla circonferenza Γ:
F
.
E
.
.
apotema
Γ
.
D
.
C
.
.
A
B
fig. 3
In fig. 4 è rappresentato il quadrilatero ABCD che non è circoscritto alla circonferenza Γ:
D
.
C
.
PERCHÈ?
.
Γ
A
B
fig. 4
OSSERVAZIONE:
•
Data una circonferenza, è sempre possibile sia inscrivervi che circoscrivervi un poligono con
un qualsiasi numero di lati.
•
Dato un poligono qualsiasi, non è sempre possile inscriverlo o circoscriverlo ad una
circonferenza.
7.2 Punti notevoli di un triangolo
Abbiamo già parlato di ortocentro, baricentro, incentro e circocentro di un triangolo (pag. 155 e
successive TOMO 1, 1° anno).
Tali “punti” vengono detti punti notevoli di un triangolo (punti, cioè, in cui si incontrano
segmenti/rette particolari, come altezze, mediane, bisettrici, assi).
A tali punti si “aggiungono” gli ex-centri.
In questa unità approfondiremo l’argomento, grazie all’introduzione dei quadrilateri, della
circonferenza/del cerchio e dei poligoni inscritti e circoscritti ad una circonferenza/un cerchio.
77
TEOREMA
Gli assi dei lati di un triangolo passano per uno stesso punto che si chiama circocentro.
C
a asse di AB
b
o
c
Hp.:
c asse di AC
o
A
*
B
*
b asse di BC
Th.:
a ∩ b ∩ c = {O}
a
Dimostrazione
Osserviamo che due dei tre assi, per esempio a e b, sono incidenti in un punto O, in quanto l’angolo
ABC è minore di un angolo piatto (cosa succede nel caso dell’angolo ABC congruente ad un angolo
piatto?) [fig. 5]:
C
b
o
c
O.
A
o
*
*
a
B
fig. 5
Poiché l’asse di un segmento è il luogo dei punti equidistanti dagli estremi del segmento si ha:
OA ≅ OB
perché O ∈ a ;
OB ≅ OC
perché O ∈ b .
Segue:
OA ≅ OC
per la proprietà transitiva della congruenza
e quindi:
O∈ c
(PERCHÉ?)
Pertanto: a ∩ b ∩ c = {O} [fig. 6]:
COSTRUISCI TU LA FIGURA
[fig. 6]
C.V.D.
78
OSSERVAZIONE:
Ricordiamo che per tre punti non allineati (i vertici A, B, C del triangolo) passa una e sola
circonferenza (teorema pag. 13)
[fig. 7]:
C
.
A
O
B
fig. 7
Si ha quindi che esiste una (ed una sola!) circonferenza circoscritta al triangolo e poiché la
perpendicolare ad ogni corda condotta dal centro della circonferenza dimezza ……………………...
CONTINUA
……………………………………………………………………………
.
C.V.D.
Questo teorema permette l’affermazione che ogni triangolo può essere inscritto in una
circonferenza il cui centro è il punto di intersezione degli assi dei lati (circocentro del triangolo).
In realtà più che di una affermazione si tratta di una conferma in quanto hai già “verificato” con il
compasso che gli assi dei lati di un triangolo si incontrano in uno stesso punto (circocentro del
triangolo) che è il centro della circonferenza circoscritta al triangolo (pag. 158 Tomo 1, 1° anno).
Possiamo, pertanto, concludere che vale il seguente:
COROLLARIO
Ogni triangolo è inscrivibile in una circonferenza il cui centro è il circocentro del triangolo.
79
TEOREMA
Le bisettrici degli angoli interni di un triangolo passano per uno stesso punto che si chiama
incentro.
C
a bisettrice dell’angolo interno di vertice A
oo
Hp.:
c
A
c bisettrice dell’angolo interno di vertice C
b
a
..
b bisettrice dell’angolo interno di vertice B
B
Th.:
a ∩ b ∩ c = {I}
Dimostrazione
Osserviamo che due delle tre bisettrici, per esempio a e b, sono incidenti in un punto I, interno al
triangolo, in quanto formano, con la trasversale AB, angoli coniugati interni non supplementari
(PERCHÉ?) [fig. 8]:
C
oo
c
b
.
A .
.
a
a e b non possono essere parallele
I
B
fig. 8
Poiché la bisettrice di un angolo è il luogo dei punti equidistanti dai lati dell’angolo, indicati con:
•
H il piede della perpendicolare condotta da I al lato AB;
•
K il piede della perpendicolare condotta da I al lato AC;
•
T il piede della perpendicolare condotta da I al lato BC,
si ha che:
IK ≅ IH
perché I ∈ a
IH ≅ IT
perché I ∈ b
e quindi:
IK ≅ IT
per la proprietà transitiva della congruenza.
80
Pertanto il punto I, essendo equidistante dai lati dell’angolo C, appartiene alla bisettrice di tale angolo,
cioè I∈ c (fig. 9):
C
oo
K.
b I
.
..
.
A
.T
a
c
B
H
fig. 9
C.V.D.
OSSERVAZIONE:
Il punto I è quindi equidistante dai tre lati del triangolo ABC per cui esiste una (ed una sola!
PERCHÉ?) circonferenza con centro in I e raggio IH (o IT o IK) inscritta nel triangolo (fig. 10):
C
K.
A
T
.
.I
.
H
B
fig. 10
Il teorema precedente permette l’affermazione che ogni triangolo può essere circoscritto ad
una circonferenza il cui centro è il punto d’intersezione delle bisettrici degli angoli interni del
triangolo (incentro).
In realtà, anche qui, più che di una affermazione si tratta di una conferma in quanto hai già
“verificato” con il compasso che le bisettrici degli angoli interni di un triangolo si incontrano in uno
stesso punto (incentro del triangolo) che è il centro della circonferenza inscritta nel triangolo [pag.
157 Tomo 1, 1° anno].
Possiamo, pertanto, concludere che vale il seguente:
COROLLARIO
Ogni triangolo è circoscrittibile
ad una circonferenza che ha come centro l’incentro del
triangolo.
81
Di seguito riportiamo, senza dimostrarlo, il seguente teorema:
TEOREMA
Le bisettrici di due angoli esterni di un triangolo e la bisettrice dell’angolo interno non adiacente
ad essi passano per uno stesso punto che si chiama ex-centro (fig. 11):
.
I1 ex-centro
I1
o
C o
..
A
B
fig. 11
Nel caso della fig. 11, il teorema ci assicura l’esistenza di una circonferenza (circonferenza exinscritta al triangolo ABC) che ha come tangenti il lato BC e i prolungamenti degli altri due lati AB
e AC (fig. 12):
.
I1
o
C o
..
A
B
fig. 12
82
Analogamente si costruiscono le altre due circonferenze ex-inscritte (fig. 13):
.
I1
C
.
I2
A
B
. I3
fig. 13
OSSERVAZIONE:
Per ora (e rimarrà così!) possiamo dire che:
“Un triangolo ha quattro punti equidistanti dalle rette dei lati: l’incentro e i tre ex-centri”.
83
TEOREMA
Le altezze di un triangolo, o i loro prolungamenti, passano per uno stesso punto detto
ortocentro.
[Ci riferiamo ad un triangolo acutangolo quindi ……… ]
C
AK altezza relativa ad BC
K
Hp.:
CT altezza relativa ad AB
S
A
BS altezza relativa ad AC
B
T
Th.:
AK ∩ BS ∩ CT = {H}
Dimostrazione
Conduciamo da ogni vertice del triangolo la parallela al lato opposto e sia DEF il triangolo così
ottenuto (fig. 14):
D
E
C
K
S
A
B
T
F
fig. 14
(PERCHÈ le rette DE, EF, FD si incontrano a due a due?)
COMPLETA:
Osserviamo che i quadrilateri ABCD e AFBC sono parallelogrammi perché i lati opposti sono a due a
due paralleli e quindi:
AD ≅ BC
perché ……………………………..
AF ≅ BC
perchè ……………………………..
Segue:
AD ≅ ….
per la proprietà transitiva della congruenza.
84
Pertanto il punto A è il punto medio del segmento …. .
Inoltre AK, essendo perpendicolare a BC, è perpendicolare anche a DF (PERCHÉ?) e quindi risulta
…………. di DF.
Analogamente si dimostra che BS è asse di …. e che CT è ……. di …. .
Pertanto le rette che “contengono” le tre altezze del triangolo ABC coincidono con gli assi del
triangolo DEF per cui, in base al teorema di pag. 54, tali rette passano per uno stesso punto H.
C.V.D.
OSSERVAZIONE:
L’ortocentro del triangolo ABC coincide con il circocentro del triangolo DEF.
TEOREMA
Le mediane di un triangolo passano per uno stesso punto (baricentro), che divide ciascuna
mediane in due parti, delle quali quella che contiene il vertice è doppia dell’altra.
AM mediana relativa a BC
C
Hp.:
//
*
CP mediana relativa ad AB
M
N
//
*
A
/
AM ∩ BN ∩ CP = {G}
B
/
P
BN mediana relativa ad AC
Th.:
AG ≅ 2GM
BG ≅ 2GN
CG ≅ 2GP
Dimostrazione
Disegnamo “per bene” due delle tre mediane, per esempio le mediane AM e BN e indichiamo con G il
loro punto di intersezione (esiste! PERCHÉ?) [fig. 15]:
C
Non riportiamo la mediana CP
//
*
//
*
A
…… per una figura più “pulita”.
M
N
/
.
P
/
B
fig. 15
85
Congiungiamo N con M (fig. 16):
C
//
*
N
M
G.
*
A
//
.
/
B
/
P
fig. 16
ed osserviamo che il segmento NM unisce i punti medi dei lati AC e BC per cui si ha (teorema pag.
153 Tomo 2, 1° anno) che:
NM // AB ∧ NM ≅
1
AB .
2
(• )
Siano ora Q ed R i punti medi rispettivamente dei lati AG e BG del triangolo ABG e congiungiamo Q
con R (fig. 17):
C
//
*
N
*
o
oQ
A
M
G.
.
/
//
x
/
P
Rx
B
fig. 17
Osserviamo che il segmento QR unisce i punti medi dei lati AG e BG per cui si ha (teorema pag. … )
che:
QR // AB ∧ QR ≅
1
AB .
2
(• • )
Dalle relazioni ( • ) e ( • • ), segue, per la proprietà transitiva della congruenza, che:
NM // QR ∧ NM ≅ QR
per cui il quadrilatero NMRQ, avendo due lati opposti paralleli e congruenti, è un parallelogramma
(pag. 127 Tomo 2, 1° anno) [fig. 18]:
C
//
*
N
*
A
o
oQ
/
G.
M
x
.. / R
P
//
x
B
fig. 18
86
Poiché in un parallelogramma le diagonali si incontrano nel loro punto medio si ha:
NG ≅ GR
(“segnare NG con il simbolo x ”)
MG ≅ GQ
(“segnare MG con il simbolo o ”)
e
[fig. 19]:
C
//
*
N
x G. o
o
x
*
A
oQ
/
.
P
M
//
/
R x
B
fig. 19
Pertanto risulta:
AQ ≅ QG ≅ GM
e
BR ≅ RG ≅ GN
cioè:
AG ≅ 2GM
e
BG ≅ 2GN .
Ripetendo lo stesso ragionamento per un’altra coppia di mediane, per esempio AM e CP, si trova che
il loro punto comune G' le divide allo stesso modo e cioè:
AG' ≅ 2G'M
e
CG' ≅ 2G'P ,
per cui la mediana AM è divisa nello stesso modo sia dalla mediana BN che dalla mediana CP e
questo implica che G ≡ G', cioè le tre mediane passano per lo stesso punto G e ciascuna di esse viene
divisa da G in due parti tali che quella che contiene il vertice è doppia dell’altra.
C.V.D.
87
7.3 I quadrilateri inscritti e circoscritti
Parlando dei poligoni inscritti e circoscritti ad una circonferenza abbiamo visto che, dato un poligono
qualsiasi, non è sempre possibile inscriverlo oppure circoscriverlo ad una circonferenza (a differenza
di quanto accade per i triangoli).
Puoi facilmente osservare …… e verificare che per qualsiasi poligono valgono le seguenti “regole”:
•
un poligono è inscrittibile in una circonferenza se gli assi dei suoi lati si incontrano tutti nello
stesso punto;
•
un poligono è circoscrittibile ad una circonferenza se le bisettrici dei suoi angoli si incontrano
tutte nello stesso punto.
Tali “regole” rappresentano in realtà “condizioni necessarie e sufficienti” perché un poligono sia
rispettivamente inscrittibile e circoscrittibile.
Le “regole” su esposte valgono per qualsiasi poligono e, quindi, anche per i quadrilateri per i quali,
però, si dimostrano anche i seguenti teoremi:
TEOREMA (sui quadrilateri inscritti)
Se un quadrilatero è inscrittibile in una circonferenza, allora i suoi angoli opposti sono
supplementari. [condizione necessaria]
A
Hp.:
ABCD inscritto in una
circonferenza di centro O
.
D
O
Th.:
B
BAD supplementare di BCD
ABC supplementare di ADC
C
Dimostrazione
Osserviamo innanzitutto che basterà dimostrare uno solo dei due punti della tesi perché l’altro si
dedurrà immediatamente dal fatto che la somma degli angoli interni di un quadrilatero è congruente
a due angoli piatti.
Indichiamo, pertanto, l’angolo BAD con α e l’angolo BCD con β (fig. 20):
A
α
.
D
O
B
β
C
fig. 20
88
e dimostriamo che α è supplementare di β, cioè che:
α + β ≅ 1 angolo piatto .
Congiungiamo il centro O con B e D (fig. 21):
A
α
.
D
O
B
β
C
fig. 21
e osserviamo che:
•
l’angolo convesso BOD è un angolo al centro che insiste sull’arco BD che contiene C;
•
l’angolo BAD è un angolo alla circonferenza che insiste sullo stesso arco BD,
quindi:
BOD ≅ 2 BAD
perché ogni angolo al centro è congruente al doppio dell’angolo alla
circonferenza che insiste sullo stesso arco,
cioè:
BOD ≅ 2 α .
Così:
•
l’angolo concavo BOD è un angolo al centro che insiste sull’arco BD che contiene A;
•
l’angolo BCD è un angolo alla circonferenza che insiste sullo stesso arco BD,
quindi:
BOD ≅ 2 BAD
cioè:
BOD ≅ 2β
[fig. 22]:
A
α
2β
O
.
D
2α
B
β
C
fig. 22
89
Poiché:
2α + 2β ≅ 2 angoli piatti
si ha:
α + β ≅ 1 angolo piatto
[Per la 2a parte del teorema vale l’osservazione riportata in precedenza, oppure si ripete un
ragionamento analogo].
C.V.D.
TEOREMA (inverso del precedente)
Un quadrilatero con gli angoli opposti supplementari è inscrittibile in una circonferenza.
[condizione sufficiente]
Osserviamo, ancora una volta, che la somma degli angoli interni di un quadrilatero è congruente a 2
angoli piatti per cui, se due angoli opposti sono supplementari, allora lo sono anche gli altri due.
Pertanto il teorema può essere enunciato nel seguente modo:
Un quadrilatero con una coppia di angoli opposti supplementari è inscrittibile in una
circonferenza.
C
ABCD quadrilatero
Hp.:
B
D
BAD + BCD ≅ 1 angolo piatto
(ABC + ADC ≅ 1 angolo piatto)
Th.:
ABCD è inscrivibile in una circonferenza
A
Dimostrazione
Poiché per tre punti non allineati passa una ed una sola circonferenza (teorema pag. 13), esiste una
circonferenza Γ che passa, per esempio, per A, B e C. Dobbiamo dimostrare che la circonferenza Γ
passa anche per D.
Ragioniamo per assurdo e supponiamo che la circonferenza Γ, passante per A, B e C, non passi anche
per D.
Si possono presentare due casi:
90
1° caso: Il punto D è esterno alla circonferenza Γ che interseca il lato CD nel punto E (fig. 23):
C
E.
.O
D
A
B
Γ
fig. 23
In tal caso osserviamo che il quadrilatero ABCE risulta inscritto nella circonferenza Γ (fig. 24):
C
E.
.O
D
A
B
Γ
fig. 24
per cui si ha:
ABC + AEC ≅ 1 angolo piatto
perché ABC e AEC sono angoli opposti di un quadrilatero
inscritto in una circonferenza,
e poiché:
ABC + ADC ≅ 1 angolo piatto
per ipotesi,
si ha:
AEC ≅ ADC
perché supplementari dello stesso angolo ABC.
Quest’ultima congruenza è un assurdo perché l’angolo AEC, esterno al triangolo CDE, deve essere
maggiore di ciascuno degli angoli interni ad esso non adiacente (teorema pag. 40 Tomo 1, 1° anno),
cioè, in particolare, deve essere:
AEC > ADC .
Per “non cadere” in un assurdo, la circonferenza Γ deve, quindi, passare anche per D.
C.V.D.
Nell’ultima parte del teorema, invece di utilizzare il 1° teorema dell’angolo esterno di un triangolo,
PROVA TU a pervenire alla tesi utilizzando il parallelismo.
(suggerimento: gli angoli AEC e ADC risultano angoli corrispondenti ……… )
91
2° caso: Il punto D è interno alla circonferenza Γ che interseca il prolungamento del lato CD nel
punto E (fig. 25):
C
D
.O
E
B
Γ
A
fig. 25
In tal caso osserviamo che ……………………………………CONTINUA TU ……………………
....……………………………………………………………………………………………………...
C.V.D.
I due teoremi precedenti si possono riassumere nel seguente:
TEOREMA
Condizione necessaria e sufficiente perché un quadrilatero sia inscrittibile in una circonferenza
è che gli angoli opposti siano supplementari.
Questo teorema permette di stabilire quando quattro punti appartengono ad una stessa circonferenza;
si può, infatti, affermare che:
“quattro punti appartengono ad una stessa circonferenza se il quadrilatero da essi individuato ha gli
angoli opposti supplementari”.
(ovviamente basta che due …………………… )
OSSERVAZIONE:
Per quanto detto sui poligoni inscrittibili (pag. 86), puoi verificare, anche con il disegno, che, se un
quadrilatero è inscrittibile in una circonferenza, il punto di intersezione dei quattro assi dei lati del
quadrilatero è il centro della circonferenza circoscritta.
92
COROLLARIO 1
Ogni rettangolo è inscrittibile in una circonferenza (PROVA TU).
COROLLARIO 2
Ogni quadrato è inscrittibile in una circonferenza (PROVA TU).
COROLLARIO 3
Ogni trapezio isoscele è inscrittibile in una circonferenza (PROVA TU).
Cosa puoi dire circa l’inscrittibilità di un rombo in una circonferenza?
TEOREMA (sui quadrilateri circoscritti)
In un quadrilatero circoscritto a una circonferenza la somma di due lati opposti è congruente
alla somma degli altri due.
[condizione necessaria]
C
.
.
Hp.: ABCD circoscritto ad una circonferenza
D
Th.:
.O
.
.
A
AB + CD ≅ AD + BC
B
Dimostrazione
Siano E, F, G e H i punti di tangenza rispettivamente dei lati AB, BC, CD e DA con la circonferenza
(fig. 26):
C
G
.
.F
D
.O
H.
A
.
E
B
fig. 26
93
Osserviamo che ogni vertice del nostro quadrilatero può essere considerato come un punto esterno alla
circonferenza dal quale vengono condotte le tangenti alla circonferenza stessa.
Si ha quindi (teorema pag. …) che:
AE ≅ AH
segmenti di tangenti condotte dal punto A;
BE ≅ BF
segmenti di tangenti condotte dal punto B;
CF ≅ CG
segmenti di tangenti condotte dal punto C;
DG ≅ DH
segmenti di tangenti condotte dal punto D.
Pertanto si ha:
AB + CD ≅ (AE + EB) + (CG + GD) ≅ (AH + BF) + (CF + DH) ≅ (AH + DH) + (BF + CF) ≅
≅ AD + BC
[GIUSTIFICA le congruenze riportate].
C.V.D.
TEOREMA INVERSO
Un quadrilatero è circoscrittibile ad una circonferenza se la somma di due lati opposti è
congruente alla somma degli altri due.
[condizione sufficiente]
C
D
Hp.: AB + CD ≅ AD + BC
Th.: ABCD è circoscrittibile in una circonferenza
A
B
Dimostrazione
Osserviamo che le bisettrici di due angoli interni del quadrilatero, per esempio degli angoli A e B, si
intersecano in un punto O (PERCHÉ?) che è equidistante dai lati AD, AB e BC.
Esiste, pertanto, una ed una sola circonferenza Γ tangente ai tre lati del quadrilatero.
Dobbiamo dimostrare che Γ è tangente anche al quarto lato CD.
Supponiamo per assurdo che Γ non risulti tangente a CD.
Tracciamo allora dal punto C la retta tangente a Γ che interseca la retta del lato AD in un punto E.
94
Si possono presentare due casi:
1° caso: il punto E è interno al lato AD (fig. 27):
C
D
E
Γ
A
B
fig. 27
In tal caso il quadrilatero ABCE risulta circoscritto a Γ per cui vale la relazione:
AB + CE ≅ AE + BC
e poiché per ipotesi è:
AB + CD ≅ AD + BC
sottraendo, membro a membro, dalla seconda relazione la prima, si ha:
AB + CD – (AB + CE) ≅ AD + BC – (AE + BC)
cioè:
AB + CD – AB – CE ≅ AD + BC – AE – BC
Semplificando, si ha:
CD – CE ≅ AD – AE
cioè:
CD – CE ≅ DE
e ancora:
CD ≅ DE + CE.
Quest’ultima congruenza è assurda per la disuguaglianza triangolare relativa al triangolo CDE (ogni
lato di un triangolo è minore della somma degli altri due).
Per “non cadere” in un assurdo, la circonferenza Γ deve, quindi, essere tangente anche al lato CD per
cui il quadrilatero ABCD è circoscritto a Γ.
C.V.D.
95
2° caso: il punto E è esterno al lato AD, cioè appartiene al suo prolungamento (fig. 28):
C
E
D
Γ
A
B
fig. 28
CONTINUA TU ……………………………………………………………………………………...
C.V.D.
I due teoremi precedenti si possono riassumere nel seguente:
TEOREMA
Condizione necessaria e sufficiente affinchè un quadrilatero sia circoscrittibile ad una
circonferenza è che la somma di due lati opposti sia congruente alla somma degli altri due.
OSSERVAZIONE:
Per quanto detto sui poligoni circoscrittibili (pag. 86), puoi verificare, anche con il disegno, che, se è
un quadrilatero è circoscrittibile ad una circonferenza, il punto di intersezione delle quattro bisettrici
degli angoli interni del quadrilatero è il centro della circonferenza inscritta.
COROLLARIO
Un quadrilatero con i lati tutti congruenti tra loro si può circoscrivere ad una circonferenza
(PROVA TU).
Relativamente alla circoscrittibilità dei seguenti quadrilateri:
•
quadrato;
•
rombo;
•
(generico) parallelogramma;
•
(generico) rettangolo,
cosa puoi dedurre in base all’ultimo corollario?
96
Problema risolto … o quasi
Siano dati una circonferenza Γ di centro O ed un suo diametro AB. Preso un punto C su Γ, conduci dal
punto A la perpendicolare alla retta OC ed indica con H il piede di tale perpendicolare: Detta K la
proiezione di C sul diametro AB, dimostra che:
1. AH ≅ CK;
2. Il quadrilatero convesso AHKC è inscrittibile in una circonferenza.
O centro della circonferenza Γ
C
Hp.:
O ∈ AB
AH ⊥ OC
.
A
O
K
CK ⊥ AB
B
1. AH ≅ CK
H
Γ
Th.:
2. AHKC è inscrittibile in una
circonferenza
Dimostrazione
Consideriamo i triangoli AOH e COK; essi hanno:
AHO ≅ CKO
entrambi retti per ipotesi;
AO ≅ OC
perché raggi della stessa circonferenza;
AOH ≅ COK
perché angoli opposti al vertice.
I due triangoli, avendo oltre all’angolo retto due altri elementi ordinatamente congruenti (che non sono
gli angoli acuti), sono congruenti per il criterio di congruenza dei triangoli rettangoli. Avranno,
pertanto, tutti gli elemento corrispondenti congruenti, in particolare AH ≅ CK e, quindi, è dimostrato
il punto 1.
Per dimostrare il punto 2., osserviamo il quadrilatero AHKC (fig. 29):
C
.
A
O
K
B
H
Γ
fig. 29
Poiché il triangolo AHC è retto in H, si ha che tale triangolo è inscritto nella semicirconferenza di
diametro AC e analogamente ……… CONTINUA TU
97
7.4 I poligoni regolari
Un poligono si dice regolare se ha tutti i lati e tutti gli angoli fra loro congruenti.
In altre parole, un poligono è regolare se è equilatero ed equiangolo.
Sono esempi di poligoni regolari:
•
il triangolo equilatero (che è anche equiangolo: è l’unico poligono regolare che ha tre lati);
•
il quadrato.
In particolare osserviamo che:
o il rombo e il quadrato sono i quadrilateri equilateri;
o il rettangolo e il quadrato sono i quadrilateri equiangoli.
Pertanto, il quadrato è l’unico quadrilatero regolare.
Vi sono, inoltre, pentagoni regolari, esagoni regolari, ettagoni regolari, ….… , poligoni regolari di n
lati ( ∀ n > 4).
[fig. 30]:
pentagono regolare
esagono regolare
ottagono regolare
fig. 30
98
TEOREMA
Ogni poligono regolare è sia inscrittibile che circoscrittibile e le due circonferenze (circoscritta è
inscritta) sono concentriche.
[Riferiamo il teorema, per semplicità, ad un esagono regolare, sottolineando che esso vale per un
qualsiasi poligono di n lati, con n ≥ 3 ].
E
*
D
*
Hp.:
*
F
AB ≅ BC ≅ CD ≅ DE ≅ EF ≅ FA
A≅ B≅ C≅ D≅ E≅ F
C
*
*
A
*
Th.:
B
1. ABCDEF è inscrittibile in una
circonferenza Γ1
2. ABCDEF è circoscrittibile in una
circonferenza Γ2
3. le circonferenze Γ1 e Γ2 hanno lo
stesso centro
Dimostrazione
Tracciamo due qualsiasi bisettrici degli angoli interni dell’esagono, per esempio degli angoli A e B e
sia O il loro punto di intersezione (PERCHÈ tali bisettrici si incontrano?)
[fig. 31]:
E
*
D
*
*
O.
F
C
*
*
A
*
B
fig. 31
Osserviamo che tali bisettrici bisecano gli angoli A e B in angoli tutti e quattro congruenti tra loro
perché metà di angoli congruenti per ipotesi (A ≅ B).
Quindi:
OAF ≅ OAB ≅ OBA ≅ OBC (“segnare tali angoli con il simbolo . ”)
[fig. 32]
99
E
*
D
*
*
O.
F
*
.
.
*
A
C
. .
*
B
fig. 32
Il triangolo AOB è quindi isoscele sulla base AB per cui:
(“segnare OA e OB con il simbolo
OA ≅ OB
” ).
Congiungiamo O con il vertice C (fig. 33):
E
*
D
*
*
O.
F
*
.
.
A
*
C
. .
*
B
fig. 33
Consideriamo, ora, i triangoli ABO e BCO; essi hanno:
OB in comune
(o OB ≅ OB per la proprietà riflessiva della congruenza);
AB ≅ BC
per ipotesi:
OBA ≅ OBC
per precedente dimostrazione.
I due triangoli, avendo due lati e l’angolo fra essi compreso ordinatamente congruenti, sono
congruenti per il 1° criterio di congruenza dei triangoli. Avranno, pertanto, tutti gli elementi
corrispondenti congruenti, in particolare:
OA ≅ OC
(“segnare OA e OC con il simbolo
OAB ≅ OCB
(“segnare OCB con il simbolo . ”).
”);
Segue, per la proprietà transitiva della congruenza, che:
OA ≅ OB ≅ OC
e
OAB ≅ OBA ≅ OBC ≅ OCB
100
per cui il triangolo BCO, congruente al triangolo ABO, è isoscele sulla base BC (fig. 34):
E
*
D
*
*
O.
F
*
.
.
*
A
. C
. .
*
B
fig. 34
Analogamente si dimostra che sono isosceli e congruenti fra loro tutti i triangoli ottenuti
congiungendo O con i vertici del poligono (fig. 35):
E
. . *
D
. .
*
F
*
.
.
*
O
.
.
*
A
. C
.
.
. .
*
B
fig. 35
Il punto O è, pertanto, equidistante da tutti i vertici del poligono per cui è il centro della circonferenza
Γ1 circoscritta al poligono (fig. 36):
E
F
D
O
.
C
Γ1
A
B
fig. 36
Inoltre O è anche il punto d’incontro delle bisettrici degli angoli interni dell’esagono per cui, per una
proprietà delle bisettrici (teorema pag. 131 Tomo 1, 1° anno), O è anche equidistante dai lati del
poligono e quindi è il centro della circonferenza inscritta nel poligono (fig. 37):
101
E
D
o
o
F
.
o O
Γ2
O è il centro sia della circonferenza
o
C
circoscritta che di quella inscritta.
o
o
A
B
fig. 37
C.V.D.
OSSERVAZIONE:
Nei poligoni regolari, grazie al teorema precedente, possono essere individuati alcuni elementi
particolari.
Riferendoci all’esagono ABCDEF e alle circonferenze circoscritta e inscritta della fig. 38 si riportano
gli elementi particolari del poligono:
E
D
.O
F
A
H
C
B
fig. 38
Il centro: è il centro O della circonferenza circoscritta e inscritta;
il raggio: è il raggio della circonferenza circoscritta (in figura il segmento OA);
l’apotema: è il raggio della circonferenza inscritta (in figura il segmento OH).
102
Continuiamo lo studio delle proprietà dei poligoni inscritti e circoscritti dimostrando i seguenti
teoremi:
TEOREMA
Se si divide una circonferenza in n parti congruenti (n ≥ 3), il poligono ottenuto congiungendo
successivamente i punti di divisione è regolare.
[Riferiamo il teorema alla suddivisione di una circonferenza in sei parti congruenti, sottolineando che
esso vale per la suddivisione di una circonferenza in n qualsiasi parti congruenti, con n ≥ 3].
A
*
*
B
F
*
O
.
Hp:
AB ≅ BC ≅ CD ≅ DE ≅ EF ≅ FA
Th:
ABCDEF poligono regolare
*
C
E
*
*
D
Dimostrazione
Ai fini della dimostrazione, dobbiamo far vedere che il poligono ABCDEF (esagono) ha lati e angoli
tutti congruenti tra loro, cioè:
AB ≅ BC ≅ CD ≅ DE ≅ EF ≅ FA
e
A≅ B≅ C≅ D≅ E≅ F .
A tale scopo, osserviamo che:
AB ≅ BC ≅ CD ≅ DE ≅ EF ≅ FA perché corde sottese da archi congruenti (teorema pag. 10)
[“segnare i lati AB, BC, CD, DE, EF, FA con il simbolo
”];
e inoltre:
A≅ B≅ C≅ D≅ E≅ F
perché angoli alla circonferenza che sottendono archi congruenti
(COROLLARIO 1 pag. 38) [“segnare gli angoli A, B, C, D, E, F
con il simbolo
”]
[fig. 39]:
103
A
*
*
B
F
*
O
.
*
C
E
*
*
D
fig. 39
(per dimostrare la congruenza degli angoli potevamo considerare i triangoli AOB, BOC, …………..
CONTINUA
………………………...)
C.V.D.
TEOREMA
Se si divide una circonferenza in n parti congruenti (n ≥ 3), il poligono circoscritto che ha i lati
tangenti nei punti di divisione è regolare.
[Riferiamo il teorema alla suddivisione di una circonferenza in sei parti congruenti, sottolineando che
esso vale per la suddivisione di una circonferenza in n qualsiasi parti congruenti, con n ≥ 3].
t1
A
G.
.
*
AB ≅ BC ≅ CD ≅ DE ≅ EF ≅ FA
t6
.N
t1 tangente in A alla circonferenza
*
B.
t2 tangente in B alla circonferenza
.F
H. *
t2
O
t5
* .M
.
C.
Hp.:
I t3
.
D
t6 tangente in F alla circonferenza
t1 ∩ t2 = {G} ; t2 ∩ t3 = {H} ;
.E
.*
……………………………………
t3 ∩ t4 = {N} ; t4 ∩ t5 = {L} ;
*.
L t4
t5 ∩ t6 = {M} ; t6 ∩ t1 = {N} .
Th.:
GHILMN poligono regolare
Dimostrazione
Ai fini della dimostrazione, dobbiamo far vedere che il poligono GHILMN (esagono) ha lati e angoli
tutti congruenti tra loro, cioè:
GH ≅ HI ≅ IL ≅ LM ≅ MN ≅ NG
e
G≅ H≅ I≅ L≅ M≅ N .
104
A tale scopo, osserviamo che:
AB ≅ BC ≅ CD ≅ DE ≅ EF ≅ FA perché corde che sottendono archi congruenti (“segnare le corde
AB, BC, … con il simbolo
”);
e inoltre:
GAB ≅ GBA ≅ HBC ≅ HCB ≅ ICD ≅ …..NFA ≅ NAF perché
angoli
alla
circonferenza
che
insistono sullo stesso arco o su archi
congruenti
(“segnare
gli
angoli
alla
circonferenza GAB, GBA, … con il
simbolo . ”)
[fig. 40]:
t1
B. .
.
G.
*
A
..
t6
.N
*
.F
H. *
t2
O
.
C.
Ci limitiamo a “segnare” solo alcune
*.
.
corde e qualche angolo alla circonferenza
.E
.*
I t3
.
D
*.
L t4
fig. 40
Pertanto i triangoli GAB, HBC, ICD, ….. , NAF sono triangoli isosceli tutti congruenti tra loro.
CONTINUA TU
Segue che il poligono ABCDEF ha …………………………………...................................................
C.V.D.
105
ESERCIZI UNITÀ 7
Conoscenza e comprensione
1) Cosa vuol dire che un poligono è inscritto in una circonferenza?
2) Cosa vuol dire che un poligono è circoscritto ad una circonferenza?
3) Quali sono i punti notevoli di un triangolo?
4) Il centro di quale circonferenza è detto ex-centro di un triangolo?
5) Vero o Falso?
a) Se un poligono è circoscritto ad una circonferenza, tutti i suoi punti sono
V
F
V
F
V
F
d) Se un triangolo è inscritto in una circonferenza, il centro della circonferenza V
F
esterni ad essa.
b) Se un poligono è inscritto in una circonferenza, i suoi lati sono corde della
circonferenza.
c) Un triangolo ottusangolo non può essere circoscritto ad una circonferenza.
coincide con l’incentro del triangolo.
e) Se una circonferenza è inscritta in un triangolo, l’incentro del triangolo è il
V
F
f) Un triangolo ammette un solo ex-centro.
V
F
g) La circonferenza inscritta e quella circoscritta ad un triangolo possono
V
F
h) Il baricentro di un triangolo equilatero è il centro della circonferenza ad esso V
F
centro della circonferenza.
essere concentriche.
circoscritta.
i) Un poligono concavo non può essere circoscritto ad una circonferenza.
V
F
j) In un circonferenza si può inscrivere un poligono concavo.
V
F
k) Se un poligono è inscritto in una circonferenza, esso è sicuramente convesso. V
F
l) Se le bisettrici dei vertici di un poligono convesso passano per uno stesso
V
F
m) Se una circonferenza è circoscritta ad un poligono convesso, gli assi dei lati V
F
punto, il poligono è inscrittibile in una circonferenza.
del poligono passano per uno stesso punto.
106
6) Esponi la CNES affinchè un quadrilatero si inscrivibile in una circonferenza.
7) Esponi la CNES affinchè un quadrilatero sia circoscrivibile ad una circonferenza.
8) Una sola delle seguenti proposizioni è vera. Quale?
a) Un trapezio è sempre inscrittibile in una circonferenza.
b) Se due angoli consecutivi di un quadrilatero sono supplementari, esso è inscrittibile in una
circonferenza.
c) Se due angoli opposti di un quadrilatero sono complementari, il quadrilatero è inscrittibile
in una circonferenza.
d) Se due angoli opposti di un quadrilatero sono supplementari, esiste sicuramente una
circonferenza circoscritta al quadrilatero.
e) Se due angoli opposti di un quadrilatero sono supplementari, esiste sicuramente una
circonferenza inscritta nel quadrilatero.
9) Sia Γ una circonferenza circoscritta al quadrilatero ABCD; quali, fra le seguenti, possono essere
le ampiezze degli angoli del quadrilatero?
a) A = 83° ; B = 75° ; C = 80° ; D = 122°.
b) A = 73° ; B = 96° ; C = 108°; D = 83°.
c) A = 106° ; B = 93° ; C = 74° ; D = 87°.
d) A = 80° ; B = 110°; C = 100°; D = 80°.
e) A = 87° ; B = 87° ; C = 97° ; D = 97°.
10) Il quadrilatero FGKL è inscritto in una circonferenza Γ di centro O; l’ampiezza dell’angolo FOG
è 114° e quella di FKL è di 45°; qual è l’ampiezza di LFG?
a) 66°;
b) 21°;
c) 78°;
d) 80°;
e) non si può determinare.
107
11) Sia Γ una circonferenza inscritta nel quadrilatero ABCD; quali, fra le seguenti, possono essere le
misure dei lati del quadrilatero?
a) AB = 42 cm; BC = 73 cm; CD = 60 cm; AD = 30 cm.
b) AB = 52 cm; BC = 52 cm; CD = 32 cm; AD = 35 cm.
c) AB = 55 cm; BC = 20 cm; CD = 32 cm; AD = 68 cm.
d) AB = 25 cm; BC = 35 cm; CD = 42 cm; AD = 18 cm.
e) AB = 25 cm; BC = 35 cm; CD = 35 cm; AD = 25 cm.
12) Il quadrilatero PQRS è circoscritto ad una circonferenza; i lati PQ e SR misurano,
rispettivamente, 14 cm e 18 cm, il lato PS è i
a) 19;
b) 22;
c) 18;
d) 8;
2
di SR. Qual è la misura di QR?
3
e) 20.
13) Quale dei seguenti poligoni non è circoscrivibile ad una circonferenza?
a) trapezio rettangolo;
b) quadrato;
c) rombo;
d) trapezio isoscele;
e) rettangolo.
14) Osserva la figura e stabilisci se le seguenti proposizioni sono vere o false.
t2
.T
.
O.
t1 e t2 rette tangenti alla circonferenza
D
.
S
t1
a) Il quadrilatero OTDS è circoscrivibile ad una circonferenza.
V
F
b) S è un punto della circonferenza circoscritta al triangolo OTD.
V
F
c) Il punto medio di OD è il centro della circonferenza circoscritta a OTDS.
V
F
d) Il centro della circonferenza inscritta nel quadrilatero OTDS appartiene
V
F
ad OD.
108
15) Dai la definizione di poligono regolare.
16) Vero o Falso?
a) I vertici di un poligono regolare dividono la circonferenza circoscritta in archi V
F
congruenti.
b) I centri della circonferenza inscritta e di quella circoscritta ad un poligono
V
F
c) L’apotema di un poligono regolare è il raggio della circonferenza circoscritta V
F
regolare sono punti distinti.
al poligono.
d) Il lato di un quadrato è congruente al doppio del raggio della circonferenza
V
F
V
F
inscritta nel quadrato.
e) Il diametro di una circonferenza è congruente alla diagonale del quadrato in
essa inscritto.
Considera i seguenti quadrilateri e completa secondo le indicazioni date:
17)
D
C
INSCRITTIBILE
SI
NO
Perché ……………………
B
A
18)
D
INSCRITTIBILE
75°
A
C
SI
NO
105°
Perché ……………………
B
109
19)
D
C
INSCRITTIBILE
135°
SI
B
A
NO
Perché ……………………
20)
C
INSCRITTIBILE
*
*
SI
*
120°
D
B
NO
Perché ……………………
A
21)
A
40°
*
B
INSCRITTIBILE
*
SI
D
35°
NO
Perché ……………………
C
110
Applicazione
1)
Nella tabella seguente sono date le ampiezze degli angoli opposti A e C di un insieme di
quadrilateri. Completa la tabella secondo le indicazioni riportate:
2)
A
C
A+C
Il quadrilatero è inscrittibile?
(scrivere SI o NO)
64°
116°
……
……
71°
110°
……
……
29°
151°
……
……
60° 28' 15''
119° 31' 45''
……
……
106° 59' 12''
73° 48''
……
……
63° 38''
116° 22''
……
……
Le ampiezze di due angoli di un quadrilatero inscritto in una circonferenza sono 46° 30' 18'' e
114° 25' 35''. Calcola le ampiezze degli altri angoli.
[133° 29' 42'' ; 65° 34' 25'']
3)
Sia dato un quadrilatero ABCD inscritto in una circonferenza. Sapendo che gli angoli di vertici
A e B hanno ampiezza rispettivamente di 58° 37'' e 60° 29' 15'', calcola l’ampiezza degli angoli
di vertici C e D.
[121° 59' 23'' ; 119° 30' 45'']
4) Sia dato un quadrilatero ABCD inscritto in una circonferenza. Sapendo che l’angolo A ha
ampiezza 81° 21' 12'' e che l’angolo B è congruente ai 2/3 di tale ampiezza, determina
l’ampiezza degli angoli B, C, D.
[54° 14' 8'' ; 98° 38' 48'' ; 125° 45' 52'']
5) In un quadrilatero inscritto in una circonferenza la somma di due angoli è 185° 41' 34'' e la loro
differenza è 31° 15' 38''. Determina l’ampiezza dei quattro angoli del quadrilatero.
[108° 28' 36'' ; 77° 12' 58'' ; 31° 31' 24'' ; 102° 47' 2'']
111
6) Nella tabella seguente sono date le lunghezze dei lati, espresse in cm, di un insieme di quadrilateri.
Completa la tabella secondo le indicazioni riportate:
AB
BC
CD
DA
AB + CD
BC + DA
Il quadrilatero è circoscrittibile?
(scrivere SI o NO)
29
34
35
20
…..
…..
…..
42
27
18
33
…..
…..
…..
35
29
18
24
…..
…..
…..
46
52
39
23
…..
…..
…..
59
46
32
45
…..
…..
…..
7) Sia ABCD un quadrilatero circoscritto ad una circonferenza. Sapendo che AB e il lato opposto CD
misurano rispettivamente 50 cm e 27 cm, determina le misure di BC e di DA, con BC ≅ 2 . DA.
[19 cm ; 38 cm]
8) Sia ABCD un quadrilatero circoscritto ad una circonferenza. Sapendo che la somma dei lati
. e che AB ≅ 2 .CD, determina le misure dei lati del
opposti AB e CD è congruente a 63 cm
quadrilatero nel caso in cui BC ≅
3
DA .
4
[42 cm ; 27 cm ; 21 cm ; 36 cm]
9) Dato il quadrilatero ABCD, figura a lato, completa la seguente
D
C
tabella in modo che il quadrilatero sia inscrittibile e circoscrittibile
(le misure dei lati sono espresse in cm):
B
A
AB
BC
CD
DA
A
35
20
…
32
…
26
1/2 AB
15
…
62°
…
2 CD
42
2/3 CD
B
C
D
109°
…
…
…
98°
…
…
74°
89°
2/3 DA
…
1/2 AB
96
2C
…
…
3B
…
78
2 DA
1/3 BC
79°
49°
…
…
112
10) Calcola l’ampiezza dell’angolo indicato con il simbolo x :
D
C
x
A
86° .
O
38°
B
Problemi
Punti notevoli di un triangolo
1) Sia data una circonferenza Γ in cui è inscritto un triangolo ABC, isoscele sulla base BC. Detto O
l’incentro del triangolo, siano rispettivamente D ed E gli ulteriori punti d’intersezione delle rette
BO e CO con Γ.
Dimostra che:
1) Il quadrilatero ADOE è un rombo;
2) ABC ≅ (EAD – BAC).
2) Dato un triangolo ABC, sia G il suo baricentro. Detto M il punto medio del segmento AG, conduci
dai punti G ed M le parallele al lato BC. Dimostra che tali parallele dividono i lati AB e AC in tre
segmenti fra loro congruenti.
3) Dato un triangolo ABC, siano M, N e P i punti medi rispettivamente dei lati AB, BC e AC.
Dimostra che:
1) I triangoli ABC e MNP hanno lo stesso baricentro;
2) L’ortocentro del triangolo MNP è il circocentro del triangolo ABC.
4) Dimostra che in ogni triangolo rettangolo la distanza del baricentro dal vertice dell’angolo retto è
congruente alla terza parte dell’ipotenusa.
5) Dato un triangolo ABC, sia H il suo ortocentro. Dimostra che il vertice C è l’ortocentro del
triangolo ABH.
113
6) Dato un triangolo ABC, retto in A, sia AH l’altezza relativa all’ipotenusa BC. Prendi un punto P
interno al segmento BH e conduci da tale punto la parallela al cateto AB. Detto K il punto
d’intersezione di tale parallele con l’altezza AH, dimostra che K è l’ortocentro del triangolo PAC.
(suggerimento: detto T il punto d’intersezione della retta PK con il cateto AC, il punto K ……)
Quadrilateri inscritti e circoscritti
7) Siano dati una circonferenza Γ ed un quadrilatero ABCD in essa inscritto, con le rette dei lati DA
e CB incidenti in un punto E. Dimostra che i triangoli ABE e DCE hanno gli angoli ordinatamente
congruenti.
8) Sia dato un trapezio ABCD circoscritto ad una circonferenza Γ di centro O. Dimostra che i
triangoli aventi per vertici il centro della circonferenza e gli estremi dei lati non paralleli sono
rettangoli.
9) Siano dati il rombo ABCD e la circonferenza di centro O in esso inscritta. Dimostra che il
quadrilatero che si ottiene congiungendo i punti di contatto tra il rombo e la circonferenza è un
rettangolo.
10) Siano dati una circonferenza Γ di centro O, un suo diametro AB e una corda CD perpendicolare ad
AB. Dimostra che il quadrilatero ACBD è circoscrittibile ad una circonferenza.
11) Dato un trapezio isoscele circoscritto ad una circonferenza Γ di centro O, dimostra che il triangolo
avente per vertici O e gli estremi di un lato obliquo è rettangolo.
12) Siano dati una circonferenza Γ di centro O e un punto P esterno a Γ. Conduci da P le tangenti alla
circonferenza ed indica con S e T i punti di contatto. Dimostra che il quadrilatero PSOT è
inscrittibile e circoscrittibile.
13) Dato un triangolo rettangolo, considera la circonferenza inscritta e dimostra che il suo diametro è
congruente alla differenza fra la somma dei cateti e l’ipotenusa.
14) Sia dato un trapezio ABCD circoscritto ad una semicirconferenza. Dimostra che la base maggiore
è congruente alla somma dei lati obliqui.
(suggerimento: unisci il centro della semicirconferenza con gli estremi della base minore …..)
114
15) Sia dato il quadrilatero ABCD inscritto in una circonferenza. Dopo aver condotto le diagonali AC
e BD, dimostra che gli angoli ACD e ABD sono congruenti.
Sai dire quali sono tutte le coppie di angoli congruenti?
Poligoni regolari
16) Dato un poligono regolare, dimostra che il poligono ottenuto unendo i punti medi dei suoi lati è
ancora regolare.
17) Dato un pentagono regolare ABCDE, conduci due diagonali (non uscenti dallo stesso vertice).
Dimostra che tali diagonali si intersecano in parti corrispondenti congruenti e che la maggiore di
esse è congruente al lato del pentagono. Classifica, poi, i poligoni in cui resta suddiviso il
pentagono.
18) Dato un esagono regolare PQRSTU, conduci le diagonali PR, PT e QU.
Dimostra che:
1. le diagonali PS e PT dividono la diagonale QU in tre parti congruenti;
2. l’angolo QPT è retto.
19) Sia dato un esagono regolare inscritto in una circonferenza Γ. Dimostra che il lato dell’esagono è
congruente al raggio di Γ.
20) Dato un esagono regolare ABCDEF, considera la diagonale AD. Dimostra che i due quadrilateri in
cui viene suddiviso l’esagono sono due trapezi isosceli congruenti.
21) Sia dato un esagono regolare ABCDEF inscritto in una circonferenza di centro O. Dimostra che
l’apotema dell’esagono è congruente alla metà del lato del triangolo equilatero inscritto nella
stessa circonferenza.
22) Sia PQRSTU un esagono regolare. Prolunga i lati UP ed RQ ed indica con V il punto di
intersezione di tali prolungamenti.
Dimostra che PQV è un triangolo equilatero.
23) Dato l’esagono regolare ABCDEF, conduci le diagonali AC, BD, DF e AE. Dimostra che i punti
di incontro di tali diagonali individuano un rombo.
115
24) Dato un pentagono regolare ABCDE, conduci due diagonali non uscenti dallo stesso vertice.
Dimostra che le due diagonali si tagliano in due parti di cui la maggiore è congruente al lato del
pentagono.
D
(suggerimento: riferendoti alla seguente figura
.
*
*
E
108°
C
F.
*
*
.
A
*
B
completa la dimostrazione “ragionando” sugli angoli)
Problemi di riepilogo
25) In una circonferenza Γ di centro O è inscritto un trapezio isoscele ABCD con la base maggiore AB
coincidente con un diametro della circonferenza. Condotte le diagonali AC e BD che si incontrano
in P, dimostra che P è l’ortocentro del triangolo ABE ottenuto prolungando i lati obliqui del
trapezio.
26) Dimostra che in ogni triangolo rettangolo la somma dei due cateti è congruente alla somma dei
diametri delle circonferenze inscritta e circoscritta al triangolo.
27) Dato un triangolo acutangolo PQR, siano:
PS l’altezza relativa al lato QR;
QT l’altezza relativa al lato PR;
PS ∩ QT = {U}.
Dimostra che il quadrilatero RTUS è inscrittibile in una circonferenza.
28) Dimostra che il raggio della circonferenza circoscritta ad un triangolo equilatero ABC è doppio del
raggio della circonferenza inscritta.
(suggerimento: dal centro O conduci l’apotema OH relativa al lato AB ……)
29) Dato un qualsiasi triangolo acutangolo, dimostra che la circonferenza avente per diametro un lato
del triangolo interseca gli altri due lati nei piedi delle rispettive altezze.
116
30) Dato un triangolo ABC, retto in A, siano:
M il punto medio del cateto AB,
N il punto medio del cateto BC,
P il punto medio del cateto AC.
Dimostra che il quadrilatero APMN è inscrittibile in una circonferenza.
31) Sia dato un triangolo equilatero ABC. Prolunga i lati AB, BC e CA, dalle parti rispettivamente di
B, C e A, dei segmenti BD, CE e AF congruenti tutti ai lati del triangolo equilatero.
Dimostra che:
1. il triangolo DEF è equilatero;
2. le circonferenze circoscritte ai triangoli ABC e DEF sono concentriche.
32) Siano dati una circonferenza Γ di centro O ed un suo diametro AB. Conduci, da parti opposte
rispetto al diametro AB, due corde AC e AD.
Dimostra che il quadrilatero che ha per vertici A, O e i punti medi delle corde AC e AD è
inscrittibile in una circonferenza.
33) Due rette r ed s, distinte e tra loro parallele, sono tagliate da una trasversale t rispettivamente nei
punti A e B. Conduci le bisettrici degli angoli alterni interni di vertici A e B ed indica con C e D i
loro punti di intersezione. Dimostra che il quadrilatero ACBD è inscrittibile in una circonferenza e
determinane il centro.
34) In una circonferenza Γ di centro O, è inscritto un triangolo ABC, isoscele sulla base AB.
Congiungi il vertice C con O e sia D il punto d’intersezione del prolungamento di CO con la
circonferenza. Dimostra che il triangolo ABD è isoscele sulla base AB.
35) Ad una circonferenza Γ di centro O è circoscritto un triangolo ABC, retto in C. Sia:
AC ∩ Γ = {H};
BC ∩ Γ = {K}.
Dimostra che il quadrilatero CHOK è un quadrato.
36) Sia dato un triangolo ABC, retto in C. Sul prolungamento del cateto AC, dalla parte di A, prendi il
punto D tale che AD ≅ AB. Dimostra che il quadrilatero ADEB, con E punto qualsiasi sul
prolungamento di BC, dalla parte di B, non è circoscrittibile ad una circonferenza.
117
37) Siano date due circonferenze Γ e Γ', tangenti internamente nel punto A. Conduci il diametro AB
della circonferenza maggiore Γ e, dal suo estremo B, traccia le tangenti BS e BT alla circonferenza
Γ'. Dimostra che il quadrilatero ASBT è circoscrittibile.
38) Sia dato il triangolo ABC, isoscele sulla base BC. Traccia la semicirconferenza di diametro BC ed
indica rispettivamente con D ed E i punti di intersezione della semicirconferenza con i lati AB e
AC. Detto F il punto d’intersezione tra BE e CD, dimostra che il quadrilatero ADFE è inscrittibile.
39) Sia dato un triangolo ABC inscritto in una circonferenza. Detto H l’ortocentro del triangolo,
riferendoti alla figura a lato:
C
E
D
G
H
.
A
F
B
dimostra che BC è bisettrice dell’angolo HBG.
(suggerimento: confronta gli angoli dei triangoli ADC e BCE; angoli alla circonferenza ……….)
118
OLIMPIADI
40) Dato un triangolo acutangolo ABC, siano U e V i piedi delle altezze uscenti dai vertici A e B.
Dimostra che l’asse di UV passa per il punto medio di AB.
[Olimpiadi della Matematica, Gara Senior, 1989]
41) Sia ABCD un quadrilatero convesso inscrivibile in una circonferenza e tale che le diagonali AC e
BD siano perpendicolari. Detto P il punto d’intersezione di AC e BD, dimostra che la
perpendicolare da P a ciascun lato biseca il lato opposto.
[Olimpiadi della Matematica, Cortona, 1995]
42) Sia ABC un triangolo tale che l’angolo ACB = 60°. Sia M il punto medio del lato AB e siano H e
K i piedi delle altezze che partono, rispettivamente, da B e da A. Dimostra che HMK è equilatero.
(suggerimento: ABHK è inscrivibile ….. )
[Olimpiadi della Matematica, Gara provinciale, 2001]
ˆ = 120° e AB = AC = 1. Quanto misura il raggio del
43) Sia ABC un triangolo isoscele tale che BAC
cerchio circoscritto?
a) 2;
b)
3
;
2
c)
2
;
2
d) 1;
e) nessuna delle precedenti
[Olimpiadi della Matematica, gara provinciale 2002]
44) Sia data una stella a cinque punte inscritta in una circonferenza. Quanto vale la somma degli
angoli con vertice nelle punte della stella?
a. 100°
b. 150°
c. 180°
d. 200°
e. i dati a disposizione sono insufficienti.
[Olimpiadi della Matematica, Giochi di Archimede, 2003]
119
45) In un triangolo ABC si tracciano le bisettrici da B e da C che incontrano rispettivamente i lati AC
e AB in D ed E. Detto I il punto d’incontro delle bisettrici, si sa che il quadrilatero IDAE è
inscrivibile in una circonferenza. Allora l’angolo in A vale:
a. 30°
b. 45°
c. 60°
d. 90°
e. non si può determinare in modo univoco
[Olimpiadi della Matematica, Giochi di Archimede, 2004]
46) In un triangolo, per ogni coppia di lati consecutivi, i due assi dei lati e la bisettrice dell’angolo
formato dai due lati si incontrano in uno stesso punto. Possiamo affermare che:
a. non esiste un triangolo con questa proprietà.
b. il triangolo è equilatero
c. il triangolo ha un angolo di 30°
d. il triangolo è rettangolo
e. il triangolo ha un angolo di 45°
[Olimpiadi della Matematica, Giochi di Archimede, 2005]
47) In un pentagono convesso ABCDE i lati BC, CD, DE sono uguali. Inoltre ogni diagonale è
parallela a un lato.
Dimostrare che ABCDE è un pentagono regolare.
[Cortona, 1989]
48) Dato un triangolo acutangolo ABC inscritto in una circonferenza di centro O, si tracci la bisettrice
dell’angolo BAC; detta D la sua intersezione con BC, si conduca da D la perpendicolare alla retta
AO e si supponga che essa incontri la retta passante per A e per C in un punto P interno al
segmento AC.
Si dimostri che AP = AB.
[Gara nazionale, 1995]
120
49) Sia ABCD un quadrilatero in una circonferenza γ. Dette rispettivamente A', B', C', D' le
intersezioni di γ con le bisettrici degli angoli in A, B, C, D del quadrilatero assegnato, si dimostri
che A'B'C'D' è un rettangolo. In quali casi A'B'C'D' è un quadrato?
La medesima costruzione può essere applicata a A'B'C'D' per ottenere un rettangolo A''B''C''D'', e
così via. Si descrivano i rettangoli così ottenuti.
[Gara Senior, 1992]
50) Un triangolo è tale che esiste un cerchio che passa per tutti i punti che
C
dividono ciascun lato in tre parti uguali. Provare che ABC è equilatero.
A
B
[Gara Senior, 1989]
51) Dimostrare che un pentagono inscritto in una circonferenza e tale che
D
ogni sua diagonale sia parallela a un lato, è necessariamente regolare.
E
[Gara provinciale, 1999]
C
.
A
B
52) Si consideri un quadrato di lato unitario; inscriviamo al suo interno una circonferenza e all’interno
di questa un esagono regolare. Quanto misura il lato dell’esagono?
.
[Giochi di Archimede, 1998]
121
53) Su una circonferenza consideriamo cinque punti che chiamiamo,
ordinatamente, A, M, B, C, D, e sia M equidistante da A e da B
(vedi figura). Siano, inoltre, E ed F rispettivamente le
intersezioni di MD con AC e di MC con BD. Si dimostri che il
quadrilatero CDEF è inscrivibile in una circonferenza.
[Olimpiadi della Matematica, gara nazionale 1989]
54) Sia Γ una circonferenza fissata e ABC un triangolo in essa inscritto. Se A', B', C' sono le
intersezioni delle bisettrici uscenti rispettivamente da A, B, C con Γ, dimostrare che esse sono le
altezze del triangolo A'B'C'.
[Olimpiadi della Matematica, gara nazionale 1991]
122
UNITÀ 8
L’EQUIVALENZA DEI POLIGONI
Il problema
Il signor X vuole calcolare l’area del terreno, adiacente alla sua casa, di forma rettangolare con i lati
che misurano 12 cm e 7 cm.
Applicherà con naturalezza e sicurezza la formula A = b · h , che esprime l’area di un rettangolo di
base b ed altezza h ( formula che ha imparato fin da piccolo).
Insieme al signor X, vogliamo, però, chiederci: “perché l’area del rettangolo si calcola in quel modo?”
Più in generale: “perché l’area di una determinata figura si calcola applicando le formule che
conosciamo?”
8.1 Figure equivalenti
Ricordiamo che viene detta figura piana, o superficie piana (finita), la parte di piano delimitata da
una o più linee chiuse non intrecciate (fig. 1):
fig. 1
[Nel nostro lavoro useremo indifferentemente i due termini]
Ad ogni figura piana si può associare la sua estensione, cioè la caratteristica di occupare una certa
parte di piano. [L’estensione è un concetto primitivo. Ricordi cosa significa?]
Ci chiediamo se è possibile definire un metodo per stabilire, per esempio, se alcune delle figure
precedenti delimitano la stessa “estensione”; cioè, se occupano la stessa parte di piano.
Sappiamo che due figure congruenti si possono sovrapporre, così che il contorno dell’una coincida
perfettamente con il contorno dell’altra e siamo portati a dire che hanno la stessa estensione (fig. 2):
123
C
C'
B
B'
D
D'
ABCD ≅ A'B'C'D'
A
A'
ABCD ≅ A'B'C'D'
⇒
fig. 2
ABCD =. A'B'C'D'
Nel caso di due figure A e B non congruenti, se, sovrapponendole, si ha che B contiene A, si dice che A
è meno estesa di B ( o A è suvvalente a B) o, anche, che B è più estesa di A ( o B è prevalente ad A)
[fig. 3]:
B
A è suvvalente a B
oppure
B è prevalente ad A
A
fig. 3
Ma come si opera quando le figure non sono sovrapponibili o lo sono solo in parte?
Nella pratica capita spesso di dover confrontare le estensioni di figure diverse fra loro: per esempio
due pareti di forma diversa; ebbene, se per dipingere due pareti, una rettangolare e l’altra quadrata, si è
utilizzata la stessa quantità di vernice, diciamo che le due pareti, pur avendo forma diversa, hanno la
stessa superficie; così un pavimento è più grande di un altro se ci vogliono più mattoni dello stesso
“tipo” per ricoprirlo; ecc.
Per poter dire se due regioni piane hanno, o non hanno, la stessa superficie, da un punto di vista
geometrico, però, si devono avere criteri ben precisi.
Diamo la seguente definizione:
Due figure piane si dicono equiestese se hanno uguale estensione.
Se F1 ed F2 sono due figure equiestese, si scrive F1 =. F2 (si legge “F1 è equiesteso a F2”).
La relazione di equiestensione gode delle seguenti proprietà che si assumono come assiomi:
proprietà riflessiva:
ogni figura F è equiestesa a se stessa ( F =.F );
proprietà simmetrica: se una figura F1 è equiestesa ad una figura F2, allora la figura F2 è equiestesa alla
figura F1 ( F1 F2 =.⇒ F2 F1 );=.
proprietà transitiva: se una figura F1 è equiestesa ad una figura F2 e F2 è equiestesa ad una figura F3 ,
.
allora F1 è equiestesa a F3 ( F1 =. F2 ∧ F2 =.F3 ⇒ F1 =F3 ).
124
La relazione di equiestensione è, quindi, una relazione di equivalenza per cui l’insieme delle figure
piane si può ripartire in classi di equivalenza: ad ogni classe appartengono tutte e sole le figure piane
che hanno la stessa estensione (area).
Poiché la relazione di equiestensione è una relazione di equivalenza, due figure equiestese si dicono,
anche, equivalenti.
Enunciamo il seguente assioma (legge di tricotomia o di esclusione):
Date due figure A e B, fra di esse sussiste una sola fra le seguenti relazioni:
.
• A = B (A ha la stessa estensione di B);
•
A<B
(A è meno estesa di B);
•
A>B
(A è più estesa di B).
8.2 Somma e differenza di superfici
Si chiama somma di due superfici piane A e B, non aventi punti in comune o aventi in comune solo
punti appartenenti al loro contorno, la superficie F formata dall’unione dei punti di A e di B.
In simboli:
F=A+B.
Le superfici A e B sono dette parti di F .
Il concetto di somma può ovviamente essere esteso a più di due superfici.
Esempio 1:
Le superfici A e B non hanno punti in comune (fig. 4):
A
B
fig. 4
La superficie F1 = A + B è formata dall’unione dei punti delle due parti distinte (fig. 5):
A
B
F1 = A + B
fig. 5
125
Esempio 2:
Le superfici C e D hanno in comune punti del loro contorno (fig. 6):
D
C
fig. 6
La superficie F2 = C + D è formata dall’unione dei punti delle due superfici date (fig. 7):
F2
F2 = C + D
fig. 7
La somma di superfici gode della proprietà commutativa e di quella associativa (PROVA TU a
scrivere tali proprietà).
Se una superficie F è somma di due superfici A e B, si dice che B è la differenza tra F ed A (o, anche,
che A è la differenza tra F e B).
In simboli:
B=F-A
(A = F - B)
Due figure F1 e F2, ottenute come somma di parti congruenti, hanno la stessa estensione e si
dicono equicomposte.
Date le figure A, B, C (fig. 8):
A
B
C
fig. 8
“componiamole” in modo diverso (fig. 9):
F1
F2
fig. 9
Le figure F1 e F2 sono equicomposte per cui avranno la stessa estensione.
126
Due figure, che si possono suddividere in modo che siano formate da parti congruenti, hanno la
stessa estensione e si dicono equiscomponibili.
Osserviamo le figure F1 e F2 (fig. 10):
B
B
C
A
A
C
F1
F2
fig. 10
Le figure F1 e F2 possono essere scomposte nello stesso numero di parti ordinatamente congruenti, per
cui risultano equiscomponibili e perciò sono equivalenti.
Non vale sempre il viceversa; esistono, infatti, figure equivalenti che non sono, però, equiscomponibili
(per esempio, un cerchio e un quadrato equivalenti non possono essere scomposti in uno stesso
numero di parti ordinatamente congruenti).
Le figure, ottenute per sottrazione di parti congruenti, hanno la stessa estensione e si dicono
equiscomponibili.
Consideriamo due rettangoli A e B tra loro congruenti (fig. 11 ):
A
B
fig. 11
127
Se, da ciascuno dei due rettangoli dati, “togliamo” due quadrati congruenti, otteniamo le figure F1 e F2
(fig. 12 ):
F1
F2
fig. 12
Le figure F1 e F2 sono equiestese perché ottenute ritagliando, appunto, da rettangoli congruenti, due
quadratini congruenti.
Le figure F1, F2 ed F3 hanno la stessa estensione perché ottenute sottraendo, da quadrati congruenti,
quattro quadratini congruenti (fig. 13 ):
F1
F2
F3
fig. 13
128
Alcuni giochi matematici, antichissimi, consistono nella scomposizione di figure piane / solide e nel
ricomporre la figura di partenza o nell’ottenere una figura nuova. Il più noto fra questi è il gioco
cinese noto come Tangram: un quadrato composto da sette forme geometriche (pezzi o tessere),
precisamente cinque triangoli rettangoli isosceli, un quadrato e un parallelogramma (fig.14):
fig.14
Con i sette pezzi del Tangram è possibile costruire tantissime figure differenti, sia geometriche che di
oggetti o animali (fig.15):
129
fig.15
PROVA TU a costruire altre figure, procedendo come segue:
1. prendi un cartoncino;
2. disegna un quadrato con lato a piacere;
3. traccia le diagonali e tutti i segmenti che uniscono i punti medi dei lati del quadrato;
4. colora le parti ottenute, come illustrato in fig. 14 (ovviamente puoi utilizzare altri colori);
5. ritaglia le parti colorate.
….. Hai costruito il tuo TANGRAM!
Per iniziare il lavoro, mescola le tue tessere e cerca di ricostruire il quadrato iniziale.
Ce l’hai fatta? Penso proprio di sì.
Procedi, allora, nella costruzione di nuove figure e ….. buon lavoro!
Puoi osservare che le figure ottenute non hanno la stessa forma per cui non sono congruenti ma sono
tutte composte con i sette pezzi dello stesso tangram, cioè dallo stesso numero di parti congruenti.
Sono, quindi, tutte figure che, pur diverse tra loro, risultano equiscomponibili.
130
8.3 Poligoni equivalenti
♦ Equiscomponibilità fra parallelogrammi
TEOREMA
Due parallelogrammi sono equivalenti se hanno ordinatamente congruenti le basi e le altezze
corrispondenti.
D
C
I
G
ABCD parallelogramma
EFGI parallelogramma
*
A
H
*
//
B
//
E
Hp.: AB ≅ EF
DH ⊥ AB ; IK ⊥ EF
K
F
DH ≅ IK
Th.: ABCD =. EFGI
Dimostrazione
Mediante un movimento rigido, trasportiamo il parallelogramma EFGI sul parallelogramma ABCD in
modo che la base EF coincida con AB e che i lati GI e CD e siano nello stesso semipiano rispetto alla
retta del lato AB. Poiché i due parallelogrammi hanno le altezze congruenti, i lati CD e GI giaceranno
sulla stessa retta (parallela ad AB).
Si distinguono quattro casi:
1° caso) G coincide con C e I coincide con D (fig. 16):
D ≡I
C ≡G
A ≡E
B ≡F
fig. 16
I due parallelogrammi si sovrappongono punto per punto per cui sono congruenti e quindi equivalenti.
2° caso) I lati CD e GI hanno “una parte” in comune (fig. 17):
D
A ≡E
I
C
B ≡F
G
fig. 17
131
Osserviamo che:
o il parallelogramma ABCD è formato dal trapezio ABCI e dal triangolo AID;
o il parallelogramma ABGI è formato dallo stesso trapezio ABCI e dal triangolo BGC.
Consideriamo, allora, i triangoli AID e BGC; essi hanno:
AD ≅ BC
perché lati opposti del parallelogramma ABCD;
AI ≅ BG
perché lati opposti del parallelogramma ABGI;
DI ≅ CG
perché differenza di segmenti congruenti (DC ≅ IG ∧ IC ≅ IC).
I due triangoli, avendo i tre lati ordinatamente congruenti, sono congruenti per il 3° criterio di
congruenza dei triangoli.
[PROVA TU a dimostrare la congruenza dei triangoli AID e BGC utilizzando, invece, il 1° criterio
di congruenza dei triangoli].
Si ha quindi che:
ABCD =. ABGI perché somme di poligoni congruenti (ABCI ≅ ABCI ∧ ADI ≅ BGC),
cioè:
ABCD =. EFGI
3° caso) I lati CD e GI hanno solo un estremo in comune (fig. 18):
C ≡I
D
A ≡E
G
B ≡F
fig. 18
Osserviamo che:
o
il parallelogramma ABCD è formato dai triangoli ABC e ADC;
o
il parallelogramma ABGI è formato dallo stesso triangolo ABC e dal triangolo BGI.
Consideriamo, allora, i triangoli ADC e BGI; essi hanno:
AD ≅ BC
perché lati opposti del parallelogramma ABCD;
AC ≅ BG
perché lati opposti del parallelogramma ABGI;
DC ≅ GI
CONTINUA TU
perché …………………………………………………………………………….
.
I due triangoli, avendo ………………………………………………………………………………...
……………………………………………………………………………………………………….. .
I parallelogrammi ABCD e ABGI sono ………………… e, quindi, …………………….. .
132
4° caso): I lati CD e GI non hanno punti in comune (fig. 19):
C
D
I
G
T
BC ∩ AI = {T}
A ≡E
B ≡F
fig. 19
Osserviamo che:
o il parallelogramma ABCD è formato dal trapezio ATCD e dal triangolo ABT;
o il parallelogramma ABGI è formato dal trapezio BGIT e dallo stesso triangolo ABT.
Consideriamo i triangoli ADI e BCG; essi hanno:
AD ≅ BC
perché ……………………………………………………….. ;
…………
……………………………………………………………….. ;
…………
……………………………………………………………….. .
I due triangoli, avendo ………………………………………………………………………………...
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
[Osserva che se ai triangoli ADI e BCG “togli” il triangolo ……………………………………….....
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………].
COROLLARIO
Un parallelogramma è equivalente ad un rettangolo che ha la base e l’altezza rispettivamente
congruenti alla base e all’altezza del parallelogramma.
La conseguenza diretta dal teorema precedente è “visualizzata” nelle figg. 20 e 21:
D
C
H
G
*
*
A
I
//
B
E
//
F
fig. 20
133
D ≡I
A
C ≡G
E
B
F
fig. 21
Illustra le figure al tuo insegnante.
♦ Equiscomponibilità fra parallelogramma e triangolo
TEOREMA
Un parallelogramma è equivalente ad un triangolo che ha la base congruente alla base del
parallelogramma ed altezza doppia di quella del parallelogramma.
G
ABCD parallelogramma
D
C
Hp.:
DH ⊥ AB ; GK ⊥ EF
EF ≅ AB
GK ≅ 2 DH
//
A H
//
E
B
K F
Th.:
ABCD =. EFG
Dimostrazione
Trasportiamo il triangolo EFG sul parallelogramma ABCD in modo che la base EF coincida con AB
(fig. 22):
G
D
A ≡E
C
K B ≡F
fig. 22
134
Conduciamo dal vertice G la parallela GI al lato AD del parallelogramma ed indichiamo con L ed M,
rispettivamente, i punti d’intersezione dei lati EG e FG con il lato DC (fig. 23):
G
M C
D L
I
A ≡E
K B ≡F
fig. 23
Poiché:
GK ≅ 2 DH
per ipotesi,
si ha:
AG ≅ 2AL ⇒ AL ≅ LG
(“segnare AL e LG con il simbolo
”)
per la corrispondenza di
e
BG ≅ 2BM ⇒ BM ≅ MG (“segnare BM e MG con il simbolo * ”)
Talete [fig. 24]:
G
*
M C
D L
I
*
A ≡E
K B ≡F
fig. 24
Consideriamo i triangoli ADL e GIL; essi hanno:
AL ≅ LG
per precedente osservazione;
DAL ≅ LGI
perché angoli alterni interni formati dalle parallele AD e GI tagliate dalla
trasversale AG (“segnare DAL e LGI con il simbolo . ”) ;
ALD ≅ GLI
perché angoli opposti al vertice (“segnare ALD e GLI con il simbolo ”).
[fig. 25]:
135
G
.
*
M C
D L
I
*
.
A ≡E
K B ≡F
fig. 25
I due triangoli, avendo un lato e i due angoli ad esso adiacenti ordinatamente congruenti, sono
congruenti per il 2° criterio di congruenza dei triangoli.
Seguendo lo stesso procedimento, si dimostra che sono congruenti i triangoli BCM e GIM (PROVA
TU) [fig. 26]:
G
.
*
D L
I
.
A ≡E
.M C
.
*
K B ≡F
fig. 26
Pertanto:
ABCD =. ABML + ADL + BCM =. ABML + GIL + MIG =. ABML + LMG =.ABG
cioè il parallelogramma ABCD e il triangolo ABG, o EFG, sono equicomposti e quindi equivalenti.
C.V.D.
Il teorema può essere formulato nel seguente modo:
Un parallelogramma è equivalente ad un triangolo che ha la stessa altezza del parallelogramma
e base doppia di quella del parallelogramma.
PROVA TU a dimostrarlo.
[suggerimento: il parallelogramma e il triangolo risultano equicomposti nello stesso quadrilatero e in
due triangoli tra loro congruenti].
136
TEOREMA
Un parallelogramma è equivalente al doppio di un triangolo che ha la stessa base e la stessa
altezza del parallelogramma (fig. 27).
D
C
*
//
A
H
B
fig. 27
PROVA TU a dimostrarlo, riferendoti alla fig. 27 .
[suggerimento: il parallelogramma risulta diviso dalla diagonale BD in due triangoli tra loro
congruenti].
Come conseguenza degli ultimi due teoremi si ha il seguente:
TEOREMA
Due triangoli che hanno basi congruenti ed altezze congruenti sono equivalenti.
PROVA TU a dimostrarlo.
[suggerimento: i due triangoli sono ordinatamente equivalenti a parallelogrammi che risultano tra loro
equivalenti] .
OSSERVAZIONE:
Dato il triangolo ABC, se conduciamo da C la parallela alla base AB, si ha che gli estremi della base
formeranno, con un qualsiasi punto di tale parallela, triangoli che risultano tutti equivalenti tra loro
(teorema precedente) .
[fig. 28]:
C3
C
A
C1
C2
B
fig. 28
137
♦ Equiscomponibilità fra triangolo e trapezio
TEOREMA
Un trapezio è equivalente ad un triangolo avente come base la somma delle basi del trapezio e
per altezza la stessa altezza.
Dimostrazione
Dato il trapezio ABCD (fig. 29):
D
A
C
H
B
fig. 29
Prolunghiamo la base AB di un segmento BE ≅ DC (“segnare BE e DC con il simbolo * ”);
congiungiamo D con E ed indichiamo con F il punto d’intersezione tra DE e BC [fig. 30]:
D
*
C
F
A
H
B
*
E
fig. 30
Vogliamo dimostrare che:
ABCD =. AED
Consideriamo i triangoli BEF e CDF; essi hanno:
BE ≅ CD
per costruzione;
BEF ≅ CDF
perché angoli alterni interni formati dalle parallele BE e CD con la trasversale
DE (“segnare BEF e CDF con il simbolo . ”);
EBF ≅ DCF
perché angoli alterni interni formati dalle parallele BE e CD con la trasversale
BC (“segnare EBF e DCF con il simbolo
”).
[fig. 31]
138
D
. *
C
F
A
H
B
*
.
E
fig. 31
I due triangoli, avendo un lato e i due angoli ad esso adiacenti ordinatamente congruenti, sono
congruenti per il 2° criterio di congruenza dei triangoli.
Il trapezio ABCD, formato dal quadrilatero ABFD e dal triangolo CDF, è, quindi, equiscomponibile
con il triangolo AED, formato dallo stesso quadrilatero ABFD e dal triangolo BEF (congruente al
triangolo CDF):
Pertanto:
ABCD =. AED
C.V.D.
♦ Equiscomponibilità tra poligono circoscritto e triangolo
TEOREMA
Ogni poligono circoscritto ad una circonferenza è equivalente ad un triangolo che ha per base il
perimetro del poligono e per altezza il raggio della circonferenza inscritta nel poligono.
[Senza perdere in generalità, riferiamo il teorema ad un esagono ABCDEF circoscritto ad una
circonferenza di centro O].
Dimostrazione
E
D
F
r
.
O
C
A
B
Congiungiamo ogni vertice dell’esagono con il centro O della circonferenza ( fig. 32 ):
139
r
fig. 32
Si ottengono tanti triangoli, aventi come base un lato del poligono e per altezza il raggio della
circonferenza, per quanti sono i lati del poligono (nel nostro caso 6).
Riportiamo, poi, su una retta s, consecutivamente, tanti segmenti per quanti sono i lati del nostro
poligono, precisamente i segmenti:
GI ≅ AB,
IL ≅ BC,
LM ≅ CD,
MN ≅ DE,
NP ≅ EF,
PQ ≅ FA (fig. 33):
.
.
.
.
.
.
.
G
I
L
M
N
P
Q
s
fig. 33
Prendiamo, in uno dei due semipiani individuati dalla retta s, un punto T che abbia distanza da s pari
ad un segmento TK congruente al raggio della circonferenza, cioè TK ≅ OH. Congiungiamo T con gli
estremi dei segmenti riportati (fig. 34):
r
s
K
fig. 34
Osserviamo che ognuno dei 6 triangoli ottenuti ha la base congruente ad un lato del poligono e tutti
hanno la stessa altezza, congruente al raggio della circonferenza.
Pertanto, per il teorema di pag. 15, si ha che:
TGI =. OAB ; TIL =. OBC ; TLM =. OCD ; TMN =. ODE ; TNP =. OEF ; TPQ =. OFA
Quindi:
ABCDEF =. TGQ
perché somma di triangoli equivalenti.
C.V.D.
140
COROLLARIO
Un poligono regolare è equivalente ad un triangolo che ha la base congruente al perimetro del
poligono e l’altezza congruente all’apotema (del poligono).
PROVA TU a dimostrarlo ( osserva che un poligono regolare è sempre …)
Quanto fatto finora ci permette di confrontare, in termini di equivalenza, alcuni poligoni particolari:
parallelogrammi, rettangoli, triangoli, quadrati, trapezi, poligoni circoscritti, poligoni regolari.
Abbiamo anche visto che è possibile determinare un triangolo equiesteso ad un rettangolo, ad un
parallelogramma, ad un trapezio, ad un poligono circoscritto ad una circonferenza, ad un poligono
regolare.
La maggior parte dei teoremi ci ha permesso, quindi, di passare da un particolare poligono di quattro
lati ad uno di tre lati, ad esso equivalente.
E se abbiamo un poligono con un numero generico n di lati?
E, in generale, come si fa a stabilire quando due poligoni qualsiasi sono equivalenti?
Il problema di stabilire se due poligoni qualsiasi sono equivalenti si risolve con un procedimento che
generalizza quanto fatto in precedenza e, precisamente, permette di determinare un triangolo
equiesteso a un dato poligono convesso con un qualsiasi numero di lati.
8.4 Costruzione di poligoni equivalenti
1 Trasformazione di un poligono convesso di n lati (n > 3) in un altro, ad esso equivalente, con n-1
lati, cioè con un lato di meno.
Sia dato, per esempio, l’esagono convesso ABCDEF (fig. 35):
E
D
F
C
A
B
fig. 35
Fissiamo tre vertici consecutivi, ad esempio C, D, E, e conduciamo, per il vertice medio D, la retta r
parallela alla diagonale EC (fig. 36):
141
E
D
F
C
r
A
B
fig. 36
Indichiamo con G il punto d’intersezione della retta del lato BC con tale parallela e uniamo E con G
(fig. 37):
E
D
F
G
C
A
r
B
fig. 37
Osserviamo che i triangoli ECD e ECG sono equivalenti in quanto hanno la stessa base EC e le altezze
congruenti perché segmenti di perpendicolari compresi tra rette parallele.
Ora:
• l’esagono ABCDEF è formato dal pentagono ABCEF e dal triangolo ECD;
• il pentagono ABGEF è formato dallo stesso pentagono ABCEF e dal triangolo ECG,
e, poiché i triangoli ECD e ECG sono equivalenti, si ha:
ABCDEF =. ABGEF perché somma di figure equivalenti.
Il poligono dato è stato così trasformato in un altro poligono, ad esso equivalente, e con un lato di
meno.
142
2 Trasformazione di un poligono convesso in un triangolo ad esso equivalente.
Applicando più volte la costruzione descritta al punto 1, si ottiene ogni volta un nuovo poligono,
equivalente a quello precedente, ma con un lato sempre in meno, fino ad avere un triangolo.
3 Trasformazione di un poligono convesso in un rettangolo ad esso equivalente.
Innanzitutto si trasforma il poligono in un triangolo equivalente e, successivamente, il triangolo in un
parallelogramma (teorema pag. 132) e questo in un rettangolo equivalente (teorema pag. 131).
4 Trasformazione di un triangolo in un altro equivalente e con un lato di lunghezza assegnata.
Dato il triangolo ABC, di base AB, si vuole costruire un altro triangolo, ad esso equivalente, con un
lato congruente ad un segmento assegnato DE.
Escludendo il caso banale in cui AB ≅ DE (in tal caso, il triangolo dato risolve il nostro problema), si
possono presentare i seguenti due casi:
1° caso): AB < DE (fig. 38):
C
A
B
.
.
D
E
fig. 38
Dimostrazione
Riportiamo sulla semiretta AB, a partire da A, il segmento AF ≅ DE (“segnare AF e DE con il simbolo
// ”) [fig. 39]:
C
A
//
B
.
.
F
D
//
.
E
fig. 39
Congiungiamo C con F; tracciamo da B la parallela a CF ed indichiamo con G il suo punto
d’intersezione con AC. Uniamo, poi, G con F (fig. 40):
143
C
G
//
A
B
F
fig. 40
Osserviamo che i triangoli CGB e FGB sono equivalenti perché hanno la stessa base GB e altezze
congruenti in quanto distanze fra rette parallele.
Analogamente sono equivalenti i triangoli CFB e CFG (PROVA TU).
Pertanto:
ABC =. AGB + CGB
;
AFG =. AGB + FGB
ma:
CGB =. FGB
e, quindi:
ABC =. AFG .
2° caso) AB > DE (fig. 41):
C
A
B
.
.
D
E
fig. 41
Dimostrazione
PROVA TU
[Segui il procedimento precedente].
5 Trasformazione di un triangolo in un altro, ad esso equivalente, avente un’altezza assegnata.
PROVA TU
[Segui il procedimento di cui al punto 4].
144
6 Trasformazione di un poligono convesso in un triangolo, ad esso equivalente, avente un lato
assegnato (caso particolare del punto 2).
PROVA TU
[Considera un poligono generico e procedi come nel punto 1, fino ad ottenere un triangolo. Trasforma
il triangolo in un altro triangolo, ad esso equivalente, con il lato assegnato (punto 4)].
7
Trasformazione di un poligono convesso in un rettangolo, ad esso equivalente, avente una
dimensione (base o altezza) congruente ad un segmento assegnato (caso particolare del punto 3).
PROVA TU
[Considera un poligono generico e, procedendo come nel punto 6, trasforma il poligono in un
triangolo con un lato congruente alla dimensione assegnata per il rettangolo. Costruisci, poi, il
rettangolo avente una delle due dimensioni congruente a quella attribuita al triangolo e l’altra
congruente alla metà dell’altezza del triangolo].
Grazie alle trasformazioni dei poligoni, siamo, ora, in grado di stabilire se due dati poligoni, P1 e P2,
sono equivalenti.
Procediamo, infatti, nel seguente modo:
I
Trasformiamo i due poligoni, P1 e P2 , in due triangoli, T1 e T2 , con T1 =.P1 e T2 P=. 2 ( punto
1-costruzione di poligoni equivalenti) per cui confrontare i due poligoni equivale a confrontare
i due triangoli.
II Trasformiamo uno dei due triangoli ottenuti, per esempio T1, in un triangolo T'1, ad esso
equivalente, con un lato, scelto come base, congruente alla base di T2 ( punto 4-costruzione di
poligoni equivalenti).
III Trasformiamo T'1 e T2 in due rettangoli, R1 ed R2 , aventi per basi le basi congruenti dei due
triangoli, con R1 ≅ T'1 e R2 ≅ T2 .
IV Confrontiamo i due rettangoli R1 ed R2 che, avendo le basi congruenti, possono portare ai seguenti
casi:
a) se le due altezze sono congruenti, i due rettangoli sono congruenti e, dunque, equivalenti; di
conseguenza, sono equivalenti i due poligoni;
b) se le due altezze non sono congruenti, i due rettangoli non sono congruenti e, dunque, non sono
equivalenti; di conseguenza, non sono equivalenti i due poligoni.
145
8.5 I teoremi di Pitagora e di Euclide
Negli studi precedenti hai applicato, dal punto di vista numerico, il teorema di Pitagora e i teoremi di
Euclide; ora, rivisitiamo questi teoremi dal punto di vista dell’equivalenza, per poi ritornare
sull’espressioni numeriche di tali teoremi.
PRIMO TEOREMA DI EUCLIDE
In un triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo che ha
per dimensioni l’ipotenusa e la proiezione di quel cateto sull’ipotenusa.
Riferendoci alla figura precedente, il teorema afferma che il quadrato Q costruito sul cateto AB è
equivalente al rettangolo R i cui lati sono la proiezione BH del cateto AB sull’ipotenusa e l’ipotenusa
stessa; cioè:
Q =. R (tesi) .
La tesi può anche essere espressa nel modo seguente:
q(AB) =. r (BH , BC) .
146
Dimostrazione
Prolunghiamo il lato FG, dalla parte di G, e indichiamo con I e J i punti di intersezione di tale
prolungamento rispettivamente con le rette dei lati DB ed EH del rettangolo (fig. 42):
fig. 42
Consideriamo i triangoli BFI e ABC; essi hanno:
BF ≅ AB
perché lati del quadrato Q;
BFI ≅ BAC
perché entrambi retti;
FBI ≅ ABC
perché complementari dello stesso angolo IBA.
I due triangoli, avendo un lato e i due angoli ad esso adiacenti ordinatamente congruenti, sono
congruenti per il 2° criterio di congruenza dei triangoli. Avranno, pertanto, tutti gli elementi
corrispondenti congruenti, in particolare:
BI ≅ BC.
Osserviamo inoltre che il quadrilatero ABIJ è un parallelogramma perché i lati opposti sono paralleli
per costruzione.
147
Ora consideriamo il parallelogramma ABIJ ( indicato in figura con P ) e il quadrato ABFG (indicato in
figura con Q) [fig. 43]:
fig. 43
Essi hanno la stessa base AB e la stessa altezza BF quindi sono equivalenti; cioè:
Q =. P .
Anche il rettangolo BDEH ed il parallelogramma ABIJ sono equivalenti perché hanno le basi BI ≅ BD
( perché ? ) e la stessa altezza BH; cioè:
R =. P .
Per la proprietà transitiva dell’equivalenza delle figure piane si ha:
Q =. R .
C.V.D.
Vale anche il teorema inverso. PROVA TU ad enunciarlo.
148
TEOREMA DI PITAGORA
In ogni triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente alla somma dei
quadrati costruiti sui due cateti.
Riferendoci alla figura precedente, il teorema afferma che il quadrato Q3 costruito sull’ipotenusa BC è
equivalente alla somma del quadrato Q1, costruito sul cateto AB, e del quadrato Q2, costruito sul
cateto AC; cioè:
Q3 =. Q1 + Q2 (tesi)
La tesi può anche essere espressa nel modo seguente:
q(BC) =. q(AB) + q(AC) .
Per dimostrare il teorema prolunghiamo l’altezza AH dalla parte di H; in questo modo il quadrato Q3
viene diviso in due rettangoli R1 ed R2 (fig. 44):
149
fig. 44
Per il primo teorema di Euclide si ha che:
Q1 =. R1
∧
Q2 =. R2
e, poiché:
Q3 =. R1 + R2 ,
segue che:
Q3 =. Q1 + Q2.
C.V.D.
Vale il seguente:
TEOREMA (INVERSO DEL TEOREMA DI PITAGORA)
Se in un triangolo la somma dei quadrati costruiti su due lati è equivalente al quadrato costruito
sul terzo lato, allora il triangolo è rettangolo.
PROVA TU a dimostrarlo.
[suggerimento: costruisci un triangolo rettangolo con i cateti congruenti a due lati del triangolo dato
….. teorema di Pitagora …..].
150
SECONDO TEOREMA DI EUCLIDE
In un triangolo rettangolo il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente
al rettangolo che ha per dimensioni le proiezioni dei cateti sull’ipotenusa.
Riferendoci alla figura precedente, il teorema afferma che il quadrato Q, costruito sull’altezza AH
relativa all’ipotenusa, è equivalente al rettangolo che ha per dimensioni le proiezioni CH e BH dei
cateti sull’ipotenusa (DH ≅ BH); cioè:
Q =. R
(tesi)
La tesi può anche essere espressa nel modo seguente:
q(AH) =. r (BH , HC) .
Per dimostrare il teorema, costruiamo il quadrato di lato AH ed il rettangolo che ha per dimensioni BH
( proiezione di AB sull’ipotenusa BC) e BJ ≅ BC (fig. 45):
fig. 45
151
Ora costruiamo il quadrato Q1 di lato AB e il quadrato Q2 di lato BH (fig. 46):
fig. 46
Per il primo teorema di Euclide, il quadrato Q1 è equivalente al rettangolo R1 (BJKH), cioè:
Q1=. R1.
Per il teorema di Pitagora applicato al triangolo ABH si ha:
Q1 =. Q + Q2
e, di conseguenza, risulta:
R1 =. Q + Q2.
Sottraendo ad ambo i membri dell’equivalenza la stessa figura Q2 si ha:
R1 – Q2 =. Q
e, osservando che la differenza di figure che compare al primo membro è il rettangolo NJKD che
indichiamo con F, si ottiene:
Q =. F .
[vedi fig. 47]:
152
fig. 47
Le dimensioni del rettangolo F sono:
ND ≅ BH
∧
NJ ≅ BJ – BN;
ma:
BJ ≅ BC
per costruzione,
e
BN ≅ BH
perché lati dello stesso quadrato,
per cui possiamo scrivere:
NJ ≅ BC – BH ≅ HC.
Segue che il rettangolo F ha per dimensioni BH e HC che sono proprio le proiezioni dei cateti
sull’ipotenusa.
C.V.D.
Vale anche il teorema inverso.
PROVA TU ad enunciarlo.
153
8.6 Espressioni metriche dei teoremi di Pitagora e di Euclide
Al fine di un lavoro organico e, ancor di più, per le applicazioni pratiche, anticipiamo, rispetto al tema
“la misura delle grandezze”(oggetto di studio nell’unità successiva), le espressioni metriche dei
teoremi di Pitagora e di Euclide.
Sarà necessario richiamare alcuni concetti, come la lunghezza dei segmenti e le aree di poligoni
(triangolo, rettangolo, quadrato …), che hai studiato negli anni precedenti.
In particolare, devi ricordare che la misura di un segmento (lunghezza) e quella di una superficie
(area) sono numeri che esprimono quante volte l’unità di misura scelta, [il metro (m) o il centimetro
(cm), per esempio, per la misura di un segmento; il metro quadrato (m2) per la misura di una
superficie], è contenuta nel segmento o nella superficie in esame.
Inoltre:
dati i segmenti AB, BC, CD, ….. , le scritture AB, BC, CD, ….. stanno ad indicare, rispetto ad una
medesima unità di misura, le corrispondenti misure dei segmenti.
Vogliamo, quindi, riscrivere le relazioni espresse dal teorema di Pitagora e dai teoremi di Euclide,
utilizzando le misure delle grandezze interessate e tenendo altresì conto che, quando si passa dalle
grandezze alle relative misure, le relazioni di equivalenza si trasformano in uguaglianze.
Riferiamo le nostre osservazioni ad un triangolo ABC, retto in A, e alle relative notazioni riportate in
fig. 48:
A
B
H
C
fig. 48
AB cateto ; AB = c
AC cateto ; AC = b
BC ipotenusa; BC = a
AH altezza relativa all’ipotenusa ; AH = h
BH proiezione del cateto AB sull’ipotenusa ; BH = c'
CH proiezione del cateto AC sull’ipotenusa ; CH = b'
fig. 48
154
Così, l’enunciato del primo teorema di Euclide assume la forma seguente:
In ogni triangolo rettangolo l’area del quadrato costruito su un cateto è uguale all’area del
rettangolo che ha per dimensioni l’ipotenusa e la proiezione del cateto stesso sull’ipotenusa.
O ancora:
In ogni triangolo rettangolo il quadrato della misura di un cateto è uguale al prodotto della
misura dell’ipotenusa per la misura della proiezione del cateto stesso sull’ipotenusa.
In forma metrica, tale teorema è espresso dalle uguaglianze:
b 2 = a . b'
;
c 2 = a . c'
Dal momento che a, b, c, h, b', c' sono numeri reali positivi (rappresentano, infatti, lunghezze),
possiamo applicare le regole del calcolo algebrico, per cui si ha:
b=
a ⋅ b'
;
c=
a ⋅ c'
(e, ovviamente, si possono applicare le formule inverse).
Così, l’enunciato del teorema di Pitagora assume la forma seguente:
In ogni triangolo rettangolo l’area del quadrato costruito sull’ipotenusa è uguale alla somma
delle aree dei quadrati costruiti sui cateti.
O ancora:
In ogni triangolo rettangolo il quadrato della misura dell’ipotenusa è uguale alla somma dei
quadrati delle misure dei cateti.
In forma metrica, tale teorema è espresso dalle uguaglianze:
a 2 = c2 + b2
Applicando le regole del calcolo algebrico, si ha:
a=
b2 + c2
E ancora:
b2 = a 2 – c 2 da cui b =
a2 − c2
c2 = a 2 – b 2 da cui c =
a 2 − b2
155
Così, l’enunciato del secondo teorema di Euclide assume la forma seguente:
In ogni triangolo rettangolo l’area del quadrato costruito sull’altezza relativa all’ipotenusa è
uguale all’area del rettangolo che ha per dimensioni le proiezione dei cateti sull’ipotenusa.
O ancora:
In ogni triangolo rettangolo il quadrato della misura dell’altezza relativa all’ipotenusa è uguale
al prodotto delle misure delle proiezioni dei cateti sull’ipotenusa.
In forma metrica, tale teorema è espresso dall’uguaglianza:
h 2 = b' . c'
Applicando le regole del calcolo algebrico, si ha:
h=
b' ⋅ c'
(e, ovviamente, si possono applicare le formule inverse).
Esempi
I cateti d in triangolo ABC, retto in C, misurano 45 cm e 60 cm. Determina il perimetro del triangolo e
le proiezioni dei cateti sull’ipotenusa.
A
AC ⊥ BC
Hp:
AC = 45 cm
BC = 60 cm
B
H
2p = ?
C
AH = ?
BH = ?
Applicando il teorema di Pitagora al triangolo rettangolo ABC si ha:
AB 2 = AC 2 + BC 2 ⇒ AB =
AC 2 + BC 2 =
45 2 + 60 2 = 2025 + 3600 = 5625 = 75 cm
2p = AB + BC + CA = 75 cm + 60 cm + 45 cm = 180 cm.
Per il 1° teorema di Euclide si ha:
2
2025 cm 2
AC 2 (45 cm)
=
=
= 27 cm
AC = AB ⋅ AH ⇒ AH =
AB
75 cm
75 cm
2
BH = AB – AH ⇒ 75 – 27 cm = 48 cm
(Per calcolare BH si poteva applicare ancora il 1° teorema di Euclide).
156
8.7 Aree dei poligoni – Area del cerchio
Come il signor X (pag. 121), applichiamo con naturalezza e sicurezza le formule relative all’area dei
poligoni e del cerchio, per poi giustificare in seguito tali formule.
Parallelogramma
A = b⋅h
h
b
Rettangolo
h
A = b⋅h
b
Quadrato
A=l2
l
Triangolo
h
A=
b⋅h
2
p=
a+b+c
(semiperimetro)
2
A=
p( p − a)( p − b)( p − c)
b
c
b
a
(formula di Erone: conseguenza del teorema di Pitagora – permette di calcolare l’area di un
triangolo, note le lunghezze dei suoi lati)
157
Rombo
D
d
h
Trapezio
A=
D⋅d
2
A=
( B + b) ⋅ h
2
o
A = b⋅h
b
b
h
B
Cerchio
C = 2π r
O
r
A= πr 2
( π = 3,14 )
Poligono circoscritto
ad una circonferenza
A = p⋅r
O
r
p = semiperimetro del poligono
Poligono regolare
A = p⋅a
.O
a = apotema del poligono (a = r)
a
p = semiperimetro del poligono
158
8.8 Applicazioni del teorema di Pitagora
Triangolo equilatero
C
l
l
h
A
H
l
B
Siano:
AB = BC = CA = l
CH = h .
∧
Ricordiamo che nel triangolo equilatero l’altezza CH relativa ad AB è anche mediana di AB (e
bisettrice dell’angolo in C) per cui:
AH = HB =
l
.
2
Applicando il teorema di Pitagora al triangolo rettangolo ACH (o BCH), si ha:
AC 2 = AH 2 + CH 2 ;
cioè:
2
l
2
2
2
2
2
2
2
2
2
l 2 = ( )2 + h2 ⇒ l = l + h2 ⇒ 4 l = l + 4 h ⇒ 4 l – l = 4 h ⇒ 3 l = 4 h
2
4
da cui:
l2 =
4 2
h ⇒ l =
3
4 2
2h
2h
h =
=
3 ;
3
3
3
cioè:
l =
2h
3
3
h =
l
3 .
2
o, anche:
h2=
3 2
l ⇒ h =
4
3 2
l
l =
3;
4
2
cioè:
Così, l’area del triangolo equilatero, nota la lunghezza del lato, è data da:
l⋅h
A=
=
2
l⋅
l
3
l2
2
=
3;
2
4
cioè:
A=
l2
3 .
4
159
A questo punto, è utile ritornare sul nostro triangolo equilatero e osservare le relazioni tra le ampiezze
degli angoli e le lunghezze dei lati nei due triangoli rettangoli in cui il triangolo ABC resta diviso
dall’altezza AH (ovviamente limitiamo le nostre osservazioni ad uno solo dei due triangoli. Perché?)
[fig. 49]:
C
30°
l
l
3
2
60°
l
2
A
H
B
fig. 49
Osserviamo che il triangolo ACH, retto in H, ha gli angoli acuti di 30° e 60° (fig. 50):
C
30°
l
l
3
2
60°
l
2
A
H
fig. 50
Si ha che:
• il cateto opposto all’angolo di 30° è la metà dell’ipotenusa;
•
il cateto opposto all’angolo di 60° è la metà dell’ipotenusa per
3 (i che è lo stesso dire che il
cateto opposto all’angolo di 60° è uguale al cateto opposto all’angolo di 30° per
3 ).
Queste relazioni e le relazioni inverse sono applicate nei problemi in cui vi sono figure con angoli di
30°,
60°,
90° ,
120° (ovviamente tali figure possono essere ottenute anche con opportune
costruzioni).
160
Risolviamo, quindi, alcuni problemi relativi a triangoli rettangoli con gli angoli acuti di 30° e 60° (in
tali problemi è stato cerchiato l’elemento noto).
Nelle figg. 51, 52 e 53 è rappresentato il triangolo PQR che è la metà di un triangolo equilatero.
Esaminiamo i vari casi:
1. Nota la lunghezza dell’ipotenusa:
R
30°
10
60°
Q
P
fig. 51
Si ha:
PQ =
PR 10
=
=5
2
2
QR =
PR
2
3 = PQ 3 = 5 3
2. Nota la lunghezza del cateto opposto all’angolo di 30°:
R
30°
60°
P
7
Q
fig. 52
Si ha:
PR = 2·PQ = 2·7 = 14
QR =
PR
2
3 = PQ 3 = 7 3
161
3. Nota la lunghezza del cateto opposto all’angolo di 60°:
R
30°
60°
P
7
Q
fig. 53
Si ha:
2 ⋅ QR
QR =
PR
2
PQ =
QR
8
PR 16 3 1
8 3
8 3
=
·
=
(oppure, direttamente: PQ =
).
=
=
2
3
2
3
3
3
3
3 ⇒ PR =
3
=
2 ⋅8
3
=
16
3
=
16 3
3
COMPLETA la risoluzione del seguente problema:
Sia dato il triangolo ABC, retto in B e con gli angoli acuti di 30° e 60°:
B
60°
A
30°
C
Sapendo che AB = 12 cm, determina il perimetro del triangolo.
Si ha:
AC = 2·AB = 12 cm = 24 cm (ricorda che il cateto opposto all’angolo di 30° è ……… );
BC = …….
quindi:
2p = AB + BC + AC = (12 + ….. + 24) cm = …….. cm .
PROVA TU a formulare e a risolvere un problema sui triangoli rettangoli, con gli angoli acuti di 30°
e di 60°, per ciascuno dei seguenti tre casi:
1°. Nota la lunghezza dell’ipotenusa;
2°. Nota la lunghezza del cateto opposto all’angolo di 30°;
3°. Nota la lunghezza del cateto opposto all’angolo di 60°.
Dopo aver “risolto” ogni triangolo, determinane perimetro e area.
162
Quadrato
D
C
d
l
A
B
Siano :
AB = BC = CD = DA = l
AC = d
La diagonale AC divide il quadrato in due triangoli rettangoli congruenti.
Applicando il teorema di Pitagora al triangolo rettangolo ABC (o ACD), si ha:
AC 2 = AB 2 + BC 2
cioè:
d2=l2+l2 ⇒ d2=2l2
da cui:
d=
2l 2 = l 2
o, anche:
l 2=
d2
2
d2
d
d 2
.
=
=
2
2
2
⇒ l=
E' utile osservare le relazioni tra le ampiezze degli angoli e le lunghezze dei lati nei due triangoli
rettangoli in cui ciascuna diagonale divide il quadrato (ovviamente, anche questa volta, limitiamo le
nostre osservazioni ad uno solo dei due triangoli. Perché?) [fig. 54]:
D
C
45°
l 2
l
45°
A
l
B
fig. 54
163
Il triangolo ABC, retto in B, ha gli angoli acuti di 45° (fig. 55):
C
45°
l 2
l
45°
l
A
B
fig. 55
Osserviamo che:
• la lunghezza della diagonale è data dal prodotto della lunghezza del lato per
• la lunghezza del lato è data dal rapporto tra la lunghezza della diagonale e
2;
2.
Queste relazioni si utilizzano nei problemi in cui vi sono figure con angoli di 45°, 90° e 135° (l’angolo
di 135° è il supplementare di 45°): tali figure possono essere ottenute anche con opportune
costruzioni.
Risolviamo, ora, alcuni problemi relativi a triangoli rettangoli con gli angoli acuti di 45° (in tali
problemi è stato cerchiato l’elemento noto).
Nelle figg. 56 e 57 è rappresentato un triangolo PQR, rettangolo isoscele, che è la metà di un quadrato
(vedi fig. 54).
Esaminiamo i vari casi:
1. Nota la lunghezza dei cateti (lati del nostro quadrato, come da fig. 54) :
R
45°
6
45°
P
6
Q
fig. 56
Si ha:
PR = PQ⋅ 2 ( = QR ⋅ 2 ) = 6 2 .
164
2. Nota la lunghezza dell’ipotenusa (diagonale del nostro quadrato, come da fig. 54):
R
45°
12
*
45°
*
P
Q
fig. 57
Si ha:
PQ = QR =
PR
2
=
12
2
=
12 2
=6 2 .
2
PROVA TU a formulare e a risolvere un problema sui triangoli rettangoli con gli angoli acuti di 45°,
per ciascuno dei seguenti due casi:
1. Nota la lunghezza dei cateti;
2. Nota la lunghezza dell’ipotenusa.
Dopo aver “risolto” ogni triangolo, determina perimetro e area.
PROVA TU a risolvere i seguenti problemi:
a) Relativamente alla figura a lato e ai dati riportati, determina il perimetro e l’area del triangolo
ABC.
C
10 cm
135°
A
B
b) Determina l’area di un triangolo isoscele che ha l’angolo al vertice di 135° e il lato che misura
13 2 cm .
c) Determina il perimetro di un quadrato che ha la diagonale di 28 cm .
165
8.9 Relazioni tra i lati dei poligoni regolari e i raggi delle circonferenze inscritte e circoscritte
• Triangolo equilatero inscritto in una circonferenza
Sia dato un triangolo equilatero ABC inscritto in una circonferenza di centro O e raggio r (fig. 58):
C
.O
A
B
r
fig. 58
E' possibile risolvere il triangolo, nota la misura del raggio della circonferenza circoscritta.
Congiungiamo il centro della circonferenza con i vertici del triangolo equilatero, ottenendo, così, tre
triangoli isosceli con un angolo al vertice di 120° (360° : 3 = 120°). Tracciamo, poi, da O, le altezze
(che risultano anche mediane e bisettrici), che formeranno sei triangoli tra loro congruenti (fig. 59):
C
r
A
.O
120°
B
H
fig. 59
Consideriamo uno di questi sei triangoli, ad esempio AHO, triangolo che, per maggiore chiarezza,
rappresentiamo ingrandito (fig. 60):
O
r
60°
30°
A
H
fig. 60
166
Si ha:
AO = r
perché raggio della circonferenza circoscritta;
AOH = 60°
perché l’altezza CH è bisettrice dell’angolo AOB (120° : 2 = 60°);
AHO = 90°
perché OH è l’altezza del triangolo AOB .
Il triangolo AOH ha gli angoli di 30° , 60° , 90° per cui, nota la misura del lato AO = r, si ha:
OH =
r
2
AH = r 3 ⇒ AB = BC = CA = 2·AH = r 3 .
2
( Inoltre: CH = CO + OH = r +
r 3
= r ).
2 2
Si ha, quindi [fig. 61]:
C
.O
r
60°
30°
A
r 3
2
r
2
B
H
fig. 61
Nota la misura del lato l del triangolo equilatero, si può trovare il valore del raggio della
circonferenza circoscritta (fig. 62):
C
.O
(completa tu, eventualmente, la figura)
l
A
B
fig. 62
Infatti, (fig. 59) da:
AO ⋅ 3
; si ha:
2
l
AO ⋅ 3
l 3
l
=
=
; cioè:
⇒ AO ⋅ 3 = l ⇒ AO =
2
2
3
3
AB = l ⇒ AH =
l
2
∧
AH =
r=
l 3
.
3
167
• Triangolo equilatero circoscritto ad una circonferenza
Sia dato un triangolo equilatero ABC circoscritto ad una circonferenza di centro O e raggio r (fig. 63):
C
.O
r
fig. 63
A
B
Tracciamo dal centro O della circonferenza le perpendicolari ai lati del triangolo equilatero e
congiungiamo O con i vertici del triangolo, ottenendo, così, i triangoli ABO, BCO e CAO.
Osserviamo che le altezze di questi triangoli sono anche mediane (perché?) e, quindi, i tre triangoli
risultano isosceli e con gli angoli al vertice di 120° (360° : 3 = 120°) [fig. 64]:
C
.O
120°
r
A
B
H
fig. 64
Il triangolo dato si può considerare scomposto in sei triangoli, tutti congruenti tra loro ( le metà dei tre
triangoli isosceli di cui in precedenza).
Consideriamo uno di questi sei triangoli, ad esempio AHO, triangolo che, per maggiore chiarezza,
rappresentiamo, ingrandito (fig. 65):
O
60°
r
30°
A
H
fig. 65
168
Si ha:
OH = r
perché raggio della circonferenza circoscritta;
AOH = 60°
perché l’altezza OH è bisettrice dell’angolo AOB (120° : 2 = 60°);
AHO = 90°
perché OH è l’altezza del triangolo AOB .
Il triangolo AOH ha gli angoli di 30° , 60° , 90° per cui, nota la misura del lato AO = r, si ha:
AO = 2r
AH =
AO ⋅ 3
2r 3
=
= r 3 da cui:
2
2
AB = BC = CA = 2·AH = 2 r 3
( Inoltre: CH = CO + OH = 2r + r = 3r )
Si ha, quindi [fig. 66]:
C
O
.
60° 60°
2r
r
30°
A
r 3
B
H
fig. 66
Nota la misura del lato l del triangolo equilatero, si può trovare il valore del raggio della
circonferenza inscritta (fig. 67):
C
.O
60°
30°
A
H
l
B
fig. 67
Infatti:
l
AB = l ⇒ AH =
2
OH = r =
∧
OH =
l
l
l⋅ 3
l 3
= 2 =
=
=
; cioè:
2⋅3
6
3
3
2 3
AH
l 3
.
6
169
• Quadrato inscritto in una circonferenza
Sia dato il quadrato ABCD inscritto in una circonferenza di centro O e raggio r (fig. 68):
D
C
.O
r
A
B
fig. 68
E' possibile risolvere il quadrato, nota la misura del raggio della circonferenza circoscritta.
Basta osservare che ciascuna delle due diagonali del quadrato è un diametro della circonferenza (fig.
69):
D
C
r
r
.O
r
r
A
B
fig. 69
Per cui:
AC = 2 r
∧
AO = OC = BO = OD = r .
Inoltre, i quattro triangoli in cui le due diagonali dividono il quadrato sono congruenti – perché? – per
cui hanno gli angoli di vertice O di 90°.
Applicando, pertanto, il teorema di Pitagora ad uno di tali triangoli, per esempio al triangolo AOB, si
ha:
AB 2 = AO 2 + BO 2 ;
cioè:
AB 2 = r 2 + r 2 ⇒ AB 2 = 2 r 2 .
Pertanto:
AB = l = r 2 .
170
Nota la misura del lato l del quadrato, si può trovare il valore del raggio della circonferenza
circoscritta (fig. 70):
D
C
.O
(completa tu la figura)
l
A
B
fig. 70
Qui applichiamo la formula inversa:
l =r 2 ⇒ r=
l
2
=
l 2
.
2
• Quadrato circoscritto ad una circonferenza
Sia dato il quadrato ABCD circoscritto ad una circonferenza di centro O e raggio r (fig. 71):
D
C
r
O.
A
B
fig. 71
E' possibile risolvere il quadrato, nota la misura del raggio della circonferenza circoscritta.
Basta osservare che il diametro della circonferenza corrisponde al lato del quadrato (fig. 72):
D
E
A
Si ha, infatti:
C
r
O
.
2r
r
F
B
fig. 72
AB = EO + OF = r + r = 2 r
171
Nota la misura del lato l del quadrato, si può trovare il valore del raggio della circonferenza inscritta
(fig. 73):
D
C
.O
(completa tu, eventualmente, la figura)
l
A
B
fig. 73
Applichiamo ancora la formula inversa:
l =2r ⇒ r=
l
.
2
• Esagono regolare inscritto in una circonferenza
Sia dato l’esagono regolare ABCDEF inscritto ad una circonferenza di centro O e raggio r (fig.74):
E
D
.O
F
C
r
A
B
fig. 74
E' possibile risolvere l’esagono, nota la misura del raggio della circonferenza circoscritta.
Basta congiungere il centro della circonferenza con i vertici dell’esagono ed osservare che si
ottengono sei triangoli equilateri (fig. 75):
E
D
.O
F
C
60°
60°
A
60°
B
fig. 75
172
Consideriamo uno di questi sei triangoli equilateri, ad esempio ABO, triangolo che, per maggiore
chiarezza, rappresentiamo, ingrandito. Il triangolo resta diviso dall’altezza OH, apotema dell’esagono,
in due triangoli rettangoli con gli angoli acuti di 30° e 60° (fig. 76):
O
30° 30°
r
60°
A
r
3
2
r
2
r
r
2
H
60°
B
fig. 76
Giustifica tu la fig. 76 e che, di conseguenza, risulta:
AB = r
OH = r 3
∧
2
• Esagono regolare circoscritto ad una circonferenza
Sia dato l’esagono regolare ABCDEF circoscritto ad una circonferenza di centro O e raggio r (fig.77):
E
D
.O
F
C
r
A
H
B
fig. 77
E' possibile risolvere l’esagono, nota la misura del raggio della circonferenza inscritta.
Basta congiungere il centro della circonferenza con i vertici dell’esagono ed osservare che si
ottengono sei triangoli equilateri (fig. 78):
E
D
.O
F
C
60°
r
60°
A
60°
H
B
fig. 78
173
Consideriamo uno di questi sei triangoli equilateri, ad esempio ABO, triangolo che, per maggiore
chiarezza, rappresentiamo, ingrandito e che resta diviso dall’altezza OH, apotema dell’esagono, in due
triangoli rettangoli con gli angoli acuti di 30° e 60° (fig. 79):
O
30° 30°
2r 3
3
2r 3
3
r
60°
60°
A
r 3
3
H r 3
B
3
fig. 79
Giustifica tu la fig. 79 e che, di conseguenza, risulta:
AB = 2r 3
3
Nota la misura del lato l dell’esagono regolare, si può trovare il valore del raggio della circonferenza
circoscritta (fig. 80):
E
D
.O
F
C
l
A
B
fig. 80
Verifica tu che risulta:
r=
l 3
.
2
174
ESERCIZI UNITÀ 8
L’EQUIVALENZA DEI POLIGONI
Conoscenza e comprensione
1)
Dai la definizione di estensione di una figura.
2)
Cosa vuol dire che due figure hanno la stessa estensione?
3)
Cosa vuol dire che due figure sono equiestese?
4)
Quale simbolo usi per indicare che due figure sono equiestese?
5)
La relazione di equiestensione fra figure del piano è una relazione di equivalenza? Giustifica la
tua risposta.
6)
Che cosa si intende per area di una figura?
7)
Se F1 e F2 sono due figure del piano, come definisci la loro somma? E la loro differenza?
8)
Cosa significa che due figure sono equiscomponibili?
9)
Quali delle seguenti figure sono equiscomponibili?
A
B
C
*
D
*
/
E
/
F
/
G
H
175
10)
Disegna tre figure equicomposte alla figura A:
11)
Vero o falso?
12)
a) Due figure congruenti sono equiestese.
V
F
b) Due figure non congruenti non sono equiestese.
V
F
c) Due figure equiestese sono sempre equiscomponibili.
V
F
d) Due figure equiscomponibili sono sempre equiestese.
V
F
e) Due figure che hanno la stessa area sono equiscomponibili.
V
F
f) Due figure equicomposte sono congruenti.
V
F
g) Due figure somma di figure equiestese, sono equiestese.
V
F
h) Due figure somma di figure congruenti sono congruenti.
V
F
i) Due figure somma di figure congruenti sono equicomposte.
V
F
Una sola delle seguenti affermazioni è vera; quale?
a) Due parallelogrammi aventi congruenti due lati consecutivi sono equiestesi.
b) Un rettangolo ed un parallelogramma aventi le basi congruenti sono equiestesi.
c) Un rettangolo ed un triangolo sono equiestesi se hanno basi congruenti e l’altezza del
rettangolo è congruente alla metà dell’altezza del triangolo.
d) Un quadrato ed un triangolo non possono mai essere equiestesi.
e) Un rombo ed un quadrato aventi lati congruenti sono equiestesi.
176
13)
Un parallelogramma è equiesteso ad un quadrato ed il lato del quadrato è congruente alla base
del parallelogramma.
Cosa puoi dire dell’altezza del parallelogramma?
14)
Un triangolo ed un parallelogramma sono equiestesi e la base del parallelogramma è la metà di
quella del triangolo. Cosa puoi dire delle loro altezze?
15)
Due triangoli sono equiestesi ed le loro basi sono congruenti; cosa puoi dire delle loro altezze?
16)
Un triangolo ed un rettangolo sono equiestesi, inoltre la base del triangolo è doppia di quella
del rettangolo. Una sola delle seguente affermazioni è vera. Quale?
a) L’altezza del triangolo è congruente all’altezza del rettangolo.
b) L’altezza del rettangolo è doppia di quella del triangolo.
c) L’altezza del rettangolo è la metà di quella del triangolo.
d) L’altezza del triangolo e quella del rettangolo non sono confrontabili.
e) L’altezza del triangolo è il triplo di quella del triangolo.
17)
Un trapezio ed un triangolo sono equiestesi e le loro altezze sono congruenti. Cosa puoi dire
della base del triangolo?
18)
Un parallelogramma ed un trapezio sono equiestesi e le loro altezze sono congruenti. Stabilisci
se le seguenti affermazioni sono vere o false.
a) La somma delle basi del trapezio è congruente alla base del parallelogramma. V
F
b) La differenza delle basi del trapezio è congruente alla base del
V
F
V
F
V
F
parallelogramma.
c) La somma delle basi del trapezio è congruente alla metà della base
del parallelogramma.
d) La somma delle basi del trapezio è congruente al doppio della base
del parallelogramma.
e) La differenza delle basi del trapezio è congruente al doppio della
V
F
base del parallelogramma.
19)
Un pentagono regolare ed un triangolo sono equiestesi ed il lato del pentagono regolare è la
quinta parte della base del triangolo. Che cosa puoi dire dell’apotema del pentagono regolare e
dell’altezza del triangolo?
177
20)
Un quadrato ed un esagono regolare sono equiestesi ed il lato del quadrato è congruente
all’apotema dell’esagono.
Una sola delle seguente affermazioni è vera. Quale?
a) Il lato dell’esagono regolare è la sesta parte del lato del quadrato.
b) Il lato del quadrato è il doppio del lato dell’esagono regolare.
c) Il lato del quadrato è il triplo del lato dell’esagono regolare.
d) Il lato del’esagono regolare è il triplo del lato del quadrato.
e) Il lato dell’esagono regolare è il doppio del lato del quadrato.
21)
Nella seguente figura MNPQ è un rettangolo e PR è un segmento parallelo QN.
a) Il triangolo NPR è equiesteso al triangolo QNM.
V
F
b) Il quadrilatero MNTQ è equiesteso al quadrilatero QNPR.
V
F
c) Il rettangolo MNPQ è equiesteso al quadrilatero QRPN.
V
F
d) Il triangolo QTR è equiesteso al triangolo QTN.
V
F
e) Il triangolo MNR è equiesteso al quadrilatero QNPR.
V
F
f) L’area del triangolo NPT è metà dell’area del triangolo QRP.
V
F
g) L’area del quadrilatero NQRP è quattro volte l’area del triangolo TRP.
V
F
h) L’area del triangolo MNQ è la metà dell’area del quadrilatero QNPR.
V
F
178
22)
Come procedi per trasformare un poligono di n lati in un altro ad esso equiesteso con n – 1 lati?
23)
Trasforma il quadrilatero ABCD nel triangolo APB ad esso equiesteso.
24)
Che cosa afferma il I teorema di Euclide?
25)
Che cosa afferma il Teorema di Pitagora?
26)
Che cosa afferma il II teorema di Euclide?
27)
Le diagonali di un quadrilatero sono fra loro perpendicolari e P è il loro punto intersezione. Una
sola delle seguente affermazioni è vera. Quale?
a) La somma dei quadrati costruiti su due lati consecutivi è equiestesa alla somma dei
quadrati costruiti sugli altri due lati.
b) La somma dei quadrati costruiti su due lati opposti è equiestesa alla somma dei quadrati
costruiti sugli altri due lati.
c) Il rettangolo che ha per dimensioni i segmenti in cui una diagonale resta divisa dal
punto P è equiesteso al rettangolo che ha per dimensioni i segmenti in cui l’altra
diagonale resta divisa dal punto P.
d) Ciascuna diagonale divide il quadrilatero in due triangoli equiestesi.
e) I triangoli rettangoli in P e aventi come ipotenusa i lati opposti del quadrilatero sono
equiestesi.
f) Ciascuna diagonale divide il quadrilatero in due triangoli in ciascuno dei quali si può
applicare il teorema di Pitagora.
179
28)
Nella seguente figura è rappresentato un triangolo rettangolo in B; quale delle seguenti
affermazioni è falsa?
a) q(BC) =. q(BD) + q(CD) ;
b) q(AB) =. r (AD , AC)
;
c) q(BD) =. q(AB) – q(AD) ;
d) q(BC) =. r (AD , AC) ;
e) r (CD , AD) =. q(AB) .
29)
Il lato di un triangolo equilatero misura 6 cm.
Una sola, fra le seguenti, è la misura del raggio della circonferenza circoscritta al triangolo.
Quale?
a)
3 cm ;
2
b)
2 3 cm ;
c)
3 cm ;
3
d)
3 cm;
2 cm .
3
e)
30)
Il lato di un triangolo equilatero misura 8 cm.
Una sola, fra le seguenti, è la misura del raggio della circonferenza inscritta nel triangolo.
Quale?
a)
16 cm ;
b)
8 3 cm ;
c)
2 3 cm
3
d)
4 3 cm ;
3
e)
6 cm .
;
180
31)
Vero o Falso?
a) La diagonale di un quadrato inscritto in una circonferenza è il doppio
V
F
V
F
c) In un triangolo rettangolo un angolo è di 60°; il lato che si oppone a tale angolo V
F
del raggio della circonferenza.
b) La misura della superficie di un quadrato inscritto in una circonferenza
è il doppio del quadrato del raggio.
è la metà dell’ipotenusa per la
2.
d) In un triangolo rettangolo un angolo è di 30°; il lato che si oppone a tale angolo V
F
è la metà dell’ipotenusa.
e) In un triangolo rettangolo con un angolo è di 45° l’ipotenusa è il doppio di uno V
F
dei cateti.
f) Il raggio di una circonferenza circoscritta ad un triangolo è la quarta parte del
V
F
g) Il raggio di una circonferenza inscritta in un triangolo è uguale al quoziente fra V
F
quoziente fra il perimetro del triangolo e la sua superficie.
la superficie del triangolo ed il semiperimetro.
h) Il raggio di un circonferenza circoscritta ad un esagono regolare è la sesta parte V
F
del perimetro dell’esagono.
32)
Un quadrato di lato 2 cm è inscritto in una circonferenza.
Una sola, fra le seguenti, è la misura dell’altezza del segmento circolare che per base il lato del
quadrato. Quale?
2 cm ;
2
a)
2 − 1 cm ;
2
b)
c) 1 cm ;
d)
(
2 − 1 cm ;
)
(
)
e) 1 + 2 cm .
181
Costruzioni
1) Riproduci il triangolo ABC in figura
C
A
B
e costruisci un parallelogramma ad esso equivalente.
2) Riproduci il triangolo PQR in figura
R
P
Q
e costruisci un rettangolo ad esso equivalente.
3) Trasforma il triangolo ABC in figura in un altro, ad esso equivalente, di base DE indicata.
C
A
B
.
.
D
E
4) Trasforma il triangolo PQR in figura in un altro, ad esso equivalente, di base ST indicata.
R
.
P
Q
S
.
T
182
5) Trasforma il quadrato ABCD in figura in un rettangolo, ad esso equivalente, di base EF assegnata.
D
C
A
B
.
.
E
F
6) Trasforma il quadrato PQRS in figura in un rettangolo, ad esso equivalente, di base AB assegnata.
S
R
P
Q
.
.
A
B
7) Dato un segmento AB, prendi su di esso un punto P in modo che il rettangolo avente per
dimensioni AP e PB sia equivalente ad un quadrato di lato l .
[suggerimento: traccia la semicirconferenza di diametro …..]
8) Riproduci, sul tuo quaderno, il poligono ABCDE in figura e trasformalo in un rettangolo
equivalente.
C
D
E
A
B
9) Disegna un triangolo qualsiasi e trasformalo in un triangolo rettangolo isoscele, ad esso
equivalente.
[suggerimento: costruisci il rettangolo doppio del triangolo e, poi, trasformalo in un quadrato, la
cui metà …..]
183
Problemi
1) Dato il triangolo ABC, traccia la mediana CM relativa al lato AB. Dimostra che i triangoli ACM e
BCM sono equivalenti.
2) Sia dato un triangolo ABC. Dimostra che ciascuna mediana divide il triangolo in due triangoli
equivalenti.
3) Dato un triangolo ABC, conduci le tre mediane AM, BN, CP e dimostra che il triangolo viene
diviso in sei triangoli equivalenti.
[suggerimento: problema 2)]
4) Dato il parallelogramma ABCD, sia DH l’altezza relativa al lato AB. Dopo aver prolungato DH di
un segmento HK ≅ DH, dimostra che il quadrilatero ADBK è equivalente al parallelogramma dato.
5) Dato il triangolo ABC, retto in C, sia M il punto medio dell’ipotenusa AB. Conduci da M le
perpendicolari MH e MK rispettivamente ai cateti AC e BC. Dimostra che il quadrilatero CHMK è
equivalente alla somma dei triangoli AMH e MBK.
6) Dato il parallelogramma PQRS, conduci le diagonali PR e QS. Dimostra che tali diagonali
dividono il parallelogramma in quattro triangoli tra loro equivalenti.
7) Dato il parallelogramma ABCD, siano M, N, P, Q i punti medi dei suoi lati. Dimostra che il
parallelogramma ABCD è equivalente al doppio del quadrilatero MNPQ.
[suggerimento: Il quadrilatero MNPQ è un ……..... ; traccia i segmenti MP e NQ ……]
8) Dato il triangolo ABC, siano M ed N i punti medi rispettivamente dei lati AB e BC. Conduci da C
la parallela al lato AB ed indica con P il suo punto d’intersezione con la retta MN. Dimostra che il
triangolo ABC è equivalente al parallelogramma AMPC.
9) Dato il quadrilatero ABCD, traccia dai suoi vertici le parallele alle diagonali AC e BD. Dimostra
che il quadrilatero ottenuto, EFGH, è equivalente al doppio del quadrilatero dato.
10) Dato il parallelogramma ABCD, indica con M il punto medio del lato AD. Traccia, poi, la
semiretta BM che incontra in E la retta CD.
Dimostra che il parallelogramma ABCD è equivalente al triangolo BCE.
184
11) Siano M ed N i punti medi rispettivamente dei lati obliqui AD e BC del trapezio ABCD. Indicato
con P il punto medio del segmento MN, dimostra che i triangoli APD e BPC sono equivalenti.
12) Sia dato il triangolo ABC, isoscele sulla base AB. Indica con M ed N i punti medi rispettivamente
di AC e BC. Detto P il punto medio del segmento MN, traccia da P:
o la retta r parallela ad AC, che incontra i lati AB e BC rispettivamente nei punti E ed F;
o la retta s parallela a BC, che incontra i lati AB e AC rispettivamente nei punti G ed I.
Dimostra che i quadrilateri AEPI e BGPF sono equivalenti.
13) Dato il rettangolo ABCD, sia M il punto medio di CD. Detti E ed F i punti medi rispettivamente
di DM e CM, traccia le semirette AE e BF ed indica con G il loro punto d’intersezione. Dimostra
che il quadrilatero ABCD è equivalente al triangolo ABG.
14) Dato il parallelogramma ABCD, traccia la diagonale AC e prendi su di essa un punto P. Conduci
da P le parallele ai lati del parallelogramma e dimostra che si ottengono quattro parallelogrammi
tra cui due sono equivalenti.
15) Dato il trapezio ABCD, indica con M ed N i punti medi rispettivamente dei lati AD e BC.
Conduci da M e da N, rispettivamente, le rette r ed s perpendicolari alle rette delle basi e siano:
o P e P' le intersezioni di r rispettivamente con le rette AB e CD;
o Q e Q' le intersezioni di s rispettivamente con le rette AB e CD.
Dimostra che il rettangolo PQQ' P' è equiesteso al trapezio dato.
16) Dato il quadrilatero ABCD, conduci la sua diagonale AC. Indicato con M il punto medio di AC,
unisci M con i vertici B e D.
Dimostra che i quadrilateri ABMD e BCDM sono equivalenti.
17) Dato il parallelogramma ABCD, sia O il punto d’intersezione delle diagonali AC e BD. Dal punto
O traccia una retta r che incontra i lati opposti AB e DC nei punti E ed F rispettivamente.
Dimostra che i quadrilateri AEFD e CFEB sono equiscomponibili.
18) Dato il parallelogramma PQRS, prolunga:
o il lato PQ, dalla parte di P, di un segmento PT ≅ PQ;
o il lato QR, dalla parte di R, di un segmento RU ≅ QR.
Dimostra che i quadrilateri PRST e PRUS sono equivalenti.
185
19) Dato il triangolo ABC, conduci le mediane AM e CN. Dimostra che i triangoli ACM e ACN sono
equivalenti.
20) Siano dati un parallelogramma ABCD e un suo punto interno P. Unisci P con i quattro vertici del
parallelogramma e dimostra che la somma dei due triangoli aventi come basi due lati opposti è
equivalente alla somma degli altri due triangoli.
[suggerimento: conduci da P le parallele ai lati …]
21) Dato il quadrato ABCD, dimostra che esso è equivalente alla metà del quadrato costruito su una
sua diagonale.
22) Dato il parallelogramma ABCD, conduci la diagonale AC e prendi sul lato DC un punto qualsiasi
P. Unisci i vertici A e B con il punto P.
Dimostra che:
1)
i triangoli ABC, ABP e ACD sono equivalenti;
2)
il parallelogramma ABCD è equivalente al doppio del triangolo ABP.
23) Dato il quadrato ABCD, conduci la diagonale AC e prendi su di essa un punto E. Traccia da E
due rette r ed s, parallele rispettivamente ad AB e ad AD e sia:
o
r ∩ AD = {F}
,
r ∩ BC = {F};
o
s ∩ AB = {H}
,
s ∩ DC = {I}.
Dimostra che i quadrilateri HBGE e DFEI sono rettangoli tra loro equivalenti.
24) Dimostra che sono equivalenti due triangoli che hanno due lati rispettivamente congruenti e
supplementari gli angoli fra essi compresi.
[suggerimento: fai in modo che i due angoli supplementari siano adiacenti ……. ]
25) Dato il triangolo ABC, siano M ed N i punti medi rispettivamente dei lati AC e BC. Dimostra che
il quadrilatero ABNM è equivalente al triplo del triangolo CMN.
[suggerimento: congiungi M ed N con il punto medio ….. ]
26) Dimostra che, unendo i punti medi dei lati di un rombo, si ottiene un rettangolo equivalente a
metà del rombo dato.
186
27) Dato un triangolo ABC, costruisci sui suoi lati i quadrati ABDE, BCFG, ACHI. Unisci gli estremi
F
dei lati dei quadrati che escono da una stesso vertice
del triangolo (figura a lato) e dimostra che i triangoli
H
C
G
AIE, DBG, FCH sono equivalenti al triangolo dato.
[suggerimento: confronta ogni triangolo con il triangolo
I
A
B
ABC (problema 24))]
E
D
28) Siano dati un triangolo ABC e due punti D ed E, interni al lato BC, tali che BD ≅ DE ≅ CE.
Traccia i segmenti AD e AE ed indica con M ed N i rispettivi punti medi.
Dimostra che il quadrilatero DENM è equivalente alla quarta parte del triangolo ABC.
[suggerimento: problema 25)]
29) Sia dato il quadrilatero ABCD circoscritto ad una circonferenza di centro O. Unisci O con i vertici
del quadrilatero e dimostra che:
ABO + DCO =. ADO + BCO
[suggerimento: teorema sui quadrilateri circoscritti …..]
30) Dato un quadrilatero ABCD, siano M ed N i punti medi rispettivamente dei lati opposti AB e DC.
Congiungi ciascuno dei punti M ed N con uno dei vertici dei rispettivi lati opposti, in modo che i
due segmenti non si intersechino. Dimostra che il quadrilatero AMCN (o MBND) è equivalente
alla metà del quadrilatero ABCD.
[suggerimento: traccia la diagonale AC ( o BD) …..]
31) Dato il parallelogramma ABCD, sia P un suo punto interno. Congiungi P con i vertici del
parallelogramma e dimostra che:
ABP + DCP =. ADP + BCP
[suggerimento: conduci da P le parallele ai lati …..]
32) Sia dato il quadrilatero ABCD con le diagonali AC e BD tra loro perpendicolari. Dimostra che:
1
ABCD =. r (AC , BD) .
2
187
Primo teorema di Euclide
33) Sia data la circonferenza Γ di centro O e diametro AB. Da un punto P di Γ conduci la
perpendicolare PH al diametro AB.
Dimostra che:
q(AP) =. r (AB , AH) .
34) Sia data una circonferenza Γ di centro O. Detto AB un suo diametro, siano:
o r una retta condotta da B tale che r ∩ Γ = {B , C};
o t la tangente in A a Γ;
o {D}= r ∩ t .
Conduci da C le distanze CH e CK rispettivamente ad AB e alla retta t.
Dimostra che:
r (AD , AK) =. r (AB , AH) .
35) Dato un triangolo ABC, conduci l’altezza CH relativa alla base AB ed indica con K e T le
proiezioni ortogonali di H rispettivamente sui lati AC e BC.
Dimostra che:
r (AC , CK) =. r (BC , CT) .
36) Sia dato un trapezio rettangolo ABCD, con la diagonale minore AC perpendicolare al lato
obliquo BC.
Dimostra che:
q(AC) =. r (AB , CD) .
37) Siano date una circonferenza Γ di centro O ed una corda AB, non passante per il centro. Condotto
il diametro AC, indica con H la proiezione di B su AC.
Dimostra che:
q(AB) =. r (AH , AC) .
38) Un trapezio ABCD, di base maggiore AB, è circoscritto ad una circonferenza di centro O. Unisci
gli estremi del lato obliquo BC con il centro della circonferenza ed indica con H il piede della
perpendicolare condotta da O al lato obliquo.
Dimostra che:
q(OB) =. r (BC , BH) .
188
Teorema di Pitagora
39) Sia dato il quadrilatero ABCD con le diagonali AC e BD tra loro perpendicolari. Dimostra che:
q(AB) + q(CD) =. q(BC) + q(DA) .
40) Dato un rettangolo ABCD, costruisci un triangolo DCE esterno al rettangolo. Dimostra che:
q(DE) + q(BE) =. q(CE) + q(AE) .
[suggerimento: conduci dal punto E P la perpendicolare ai lati …..].
41) Sia dato un trapezio rettangolo ABCD con la diagonale minore AC perpendicolare al lato obliquo
BC. Dimostra che il quadrato costruito sulla base maggiore AB è equivalente alla somma dei
quadrati costruiti sugli altri tre lati del trapezio.
42) Dato un triangolo rettangolo isoscele, dimostra che il quadrato costruito su un cateto è equivalente
alla metà del quadrato costruito sull’ipotenusa.
43) Sia dato il triangolo PQR, retto in R e con RQ > RP. Dopo aver condotto l’altezza RT, dimostra
che:
q(QR) – q(PR) =. q(QT) – q(PT) .
44) Dato un quadrato ABCD, sia P un suo punto interno. Unisci P con i vertici del quadrato e conduci
D
da P le distanze dai lati del quadrato (figura a lato).
S
C
Dimostra che la somma dei quadrati costruiti sulle
distanze di P dai vertici è doppia della somma dei
P
T
K
quadrati costruiti sulle distanze di P dai lati del
quadrato.
A
H
B
45) Dato il quadrato PQRS, dimostra che il quadrato costruito sulla diagonale PR è doppio del
quadrato dato.
46) Sia dato un triangolo ABC con gli angoli in A ( ≅ α) e in B ( ≅ β) acuti e tali che α < β. Conduci
C
l’altezza CH relativa al lato AB (figura a lato).
Dimostra che:
q(AC) – q(BC) =. q(AH) – q(BH) .
α
A
β
H
B
189
Secondo teorema di Euclide
47) Siano dati un trapezio isoscele ABCD e la circonferenza Γ in essa inscritta. Dimostra che il
quadrato costruito sul diametro di Γ è equivalente al rettangolo che ha per dimensioni le basi del
trapezio.
48) Dato un triangolo rettangolo ABC, sia CH l’altezza relativa all’ipotenusa AB. Dimostra che:
q(AC) – q(AH) =. r (AH , BH) .
49) Sia dato il trapezio isoscele ABCD, di base maggiore AB e base minore CD, circoscritto ad una
circonferenza di centro O e raggio r.
Dimostra che:
q(r) =. r (
AB CD
,
).
2
2
50) In una circonferenza Γ, di centro O, traccia una corda AB e il diametro CD perpendicolare alla
corda. Detto M il punto d’intersezione di CD e AB, dimostra che:
q(
AB .
) = r (CM , DM) .
2
51) Data una circonferenza Γ di centro O e diametro AB, sia CD una corda perpendicolare ad AB.
Detto E il punto d’intersezione di AB e CD, dimostra che il quadrato costruito su CD è
equivalente al quadruplo del rettangolo che ha per dimensioni AE e BE.
52) Utilizzando il secondo teorema di Euclide, costruisci un quadrato equivalente ad un rettangolo
assegnato.
[suggerimento: prolunga una dimensione del rettangolo di un segmento congruente all’altra
dimensione; prendi il punto medio O ….. traccia la semicirconferenza di centro ….. ]
53) Data una semicirconferenza di centro O e diametro AB, prendi un punto P su di essa e siano r, s e
t le tangenti alla semicirconferenza condotte rispettivamente da A, B e P.
Se:
r ∩ t ={R};
s ∩ t ={Q},
dimostra che:
1
r (AR , BQ) =.
q(AB) .
4
190
Problemi di riepilogo sull’equivalenza
54) Dato un triangolo equilatero ABC, dimostra che il quadrato costruito sull’altezza è equivalente al
triplo del quadrato costruito su metà lato.
[suggerimento: costruisci il quadrato su un lato del triangolo e dividilo in …..]
55) Sia data una circonferenza Γ di centro O e diametro AB. Considera un punto P di Γ e traccia la
perpendicolare PH ad AB. Dimostra che si ha:
q(PH) =. r (AH , HB)
56) Siano dati un rettangolo ABCD ed un punto P interno ad esso. Unisci P con i vertici del rettangolo
e dimostra che:
q(PA) + q(PC) =. q(PB) + q(PD) .
57) Sia dato un triangolo ABC, retto in C. Prendi sui cateti AC e BC rispettivamente i punti D ed E e
dimostra che:
q(AD) + q(BE) =. q(AB) + q(DE) .
58) Dato il triangolo ABC, sia M il punto medio del lato AC. Traccia da M la retta r parallela ad AB e
da B la retta s parallela ad AC. Detto N il punto d’intersezione delle rette r ed s, dimostra che:
ABC =. ABNM .
59) Sia dato un trapezio isoscele ABCD. Condotta l’altezza DK relativa alla base maggiore AB,
dimostra che:
1
BHD =. ABCD .
2
60) Sia dato un parallelogramma ABCD in cui la diagonale BD è perpendicolare al lato AD. Dimostra
che:
q(AC) =. 3 q(BC) .
61) Dato il parallelogramma ABCD, prolunga il lato AB, dalla parte di A, di un segmento AE ≅ AB e
il lato BC, dalla parte di C, di un segmento CF ≅ BC. Dimostra che i quadrilateri EACD e ACFD
sono equivalenti.
62) Siano dati una circonferenza Γ di centro O ed un punto P esterno a Γ. Conduci da P una delle due
tangenti alla circonferenza ed indica con A il punto di tangenza. Traccia il diametro AB e il
segmento BP che interseca Γ nel punto C. Dimostra che:
q(AP) =. r (PB , PC) .
191
63) Dato un trapezio ABCD, di base maggiore AB e base minore CD, indica con M ed N i punti medi
rispettivamente dei lati AD e BC.
Dimostra che:
ADN =. BCN .
64) Relativamente alla seguente figura, dimostra che, dati due segmenti a e b, si ha:
q(a + b) =. q(a) + q(b) + 2r (a , b)
b
a
a
b
La relazione data è l’interpretazione geometrica di un particolare prodotto notevole.
Di quale?
65) Relativamente alla seguente figura, dimostra che, dati due segmenti a e b, con a > b, si ha:
q(a – b) =. q(a) + q(b) – 2r (a , b)
a
b
b
a
La relazione data è l’interpretazione geometrica di un particolare prodotto notevole.
Di quale?
192
Problemi sulle aree dei poligoni.
Espressioni metriche dei teoremi di Pitagora e di Euclide.
66) Sia dato un trapezio rettangolo ABCD con la base maggiore AB di 66 cm, l’altezza di 48 cm e il
lato obliquo di 60 cm. Calcola il perimetro e l’area del trapezio.
[204 cm ; 2304 cm2]
67) In un parallelogramma ABCD, la somma della base AB e dell’altezza relativa DK è 60 cm e AB
3
è i di DH. Calcola l’area del parallelogramma.
4
[864 cm2]
68) In un triangolo ABC, retto in C, l’ipotenusa misura 50 cm e la proiezione del cateto AC
sull’ipotenusa 18 cm. Determina il perimetro e l’area del triangolo.
[120 cm ; 600 cm2]
69) La somma dei due cateti di un triangolo ABC, retto in C, è 91 cm e uno è i
3
dell’altro. Calcola il
4
perimetro del triangolo e la misura dell’altezza relativa all’ipotenusa.
[105 cm ; 31,2 cm]
70) L’ipotenusa di un triangolo rettangolo misura 90 cm . Determina l’area del triangolo, sapendo che
la differenza tra i due cateti è 18 cm .
[suggerimento: indica con x la misura di un cateto, …..]
[1944 cm2]
71) La somma dei due cateti di un triangolo rettangolo è 119 cm e la loro differenza è 17 cm .
Determina il perimetro, l’area e le proiezioni dei cateti sull’ipotenusa.
[204 cm ; 1734 cm2 ; 30,6 cm ; 54,4 cm]
72) In un triangolo rettangolo l’ipotenusa è i
5
di un cateto e il perimetro è 60 cm . Determina l’area
3
del triangolo e le proiezioni dei cateti sull’ipotenusa.
[150 cm2 ; 9 cm ; 16 cm]
73) Sia dato il rombo ABCD di lato 18 cm . Sapendo che un angolo misura 60°, calcola l’area del
rombo.
[162 3 cm]
193
74) Il pentagono PQRST (figura a lato) è diviso dalla diagonale TR nel rettangolo PQRT, le cui
dimensioni sono una doppia dell’altra, e nel triangolo equilatero TRS,
S
di lato 18 cm .
Calcola:
a) il perimetro del pentagono;
T
R
P
Q
[72 cm ; 81(2 +
3 ) cm2 ; 2 3 ]
b) l’area del pentagono;
c) il rapporto fra l’area del rettangolo e quella del triangolo.
3
3
dell’altro e che la loro
4
differenza è 8 cm, calcola l’ipotenusa e il raggio della circonferenza circoscritta al triangolo.
75) Sia dato un triangolo ABC, retto in C. Sapendo che i cateti sono uno i
[40 cm ; 20 cm ]
76) Nel triangolo rettangolo ABC di ipotenusa AB e altezza CH, la mediana CM è lunga 50 cm.
L’altezza CH relativa all’ipotenusa è
24
del segmento HM. Calcola:
7
a) il perimetro e l’area del triangolo HMC;
b) il perimetro e l’area del triangolo ABC.
[2pHMC = 92 cm; AHMC = 336 cm2; 2pABC = 240 cm; AABC = 2400 cm2]
77) In una circonferenza di diametro AB, la corda AC è uguale ai
4
del diametro. Sapendo che l’area
5
del triangolo ABC è 294 cm2 , determina il perimetro di tale triangolo.
[84 cm]
78) Le proiezioni dei cateti di un triangolo rettangolo sono una i
9
dell’altra; e il cateto maggiore
16
supera di 32 cm il cateto minore. Determina il perimetro del triangolo.
[384 cm]
79) In un triangolo rettangolo un cateto è
5
dell’ipotenusa e l’area è di 480 cm2 . Determina il
13
perimetro del triangolo.
[120 cm]
194
80) Il cateto AB di un triangolo rettangolo ABC è i 5 del cateto AC e l’ipotenusa è 169 cm. Calcola
12
l’area delle due parti in cui il triangolo rimane diviso dall’altezza relativa all’ipotenusa AH. Detta,
poi, AM la mediana relativa all’ipotenusa, calcola il perimetro e l’area del triangolo AHM.
[750 cm2; 4320 cm2; 204 cm; 1785 cm2]
81) Dato il triangolo ABC, rettangolo in A, traccia l’altezza AH e siano D ed E le proiezioni di H
rispettivamente sui cateti AC e AB. Sapendo che AE = 4 e che il perimetro di ABC misura 50
HE
3
cm, determina la misura dell’altezza AH.
[10 cm]
82) Dato il triangolo ABC, rettangolo in A, traccia l’altezza AH e indica con D ed E le proiezioni di H
rispettivamente sui cateti AC e AB. . Sapendo che AH =
5
625
cm2,
AE e che l’area di ABC è
4
6
determina il perimetro del trapezio.
[50 cm]
83) In un triangolo rettangolo la proiezione di un cateto sull’ipotenusa è 3 del suo cateto stesso,
5
mentre la proiezione dell’altro cateto misura 64 cm. Determina il perimetro del triangolo.
[240 cm]
84) Il rapporto tra le proiezioni dei cateti sull’ipotenusa di un triangolo rettangolo è 9 e l’ipotenusa
16
misura 75 cm. Calcola perimetro e area del triangolo.
[120 cm; 1350 cm2]
85) In un triangolo rettangolo il cateto minore misura 30 cm e la differenza tra le proiezioni dei cateti
sull’ipotenusa è 14 cm . Calcola:
a. il perimetro del triangolo;
b. l’area del triangolo;
c. il rapporto tra le aree dei due triangoli in cui il triangolo dato viene diviso
[120 cm]
[600 cm2]
[9]
16
[suggerimento: indica con x la misura di una delle due proiezioni, .., equazione di 2° grado, ..]
195
86) Un rombo ABCD ha le misure delle diagonali espresse, in metri, dai valori x e y, soluzioni del
seguente sistema:
( x − 2 ) 2 − ( y − 3) 2 + 5 = ( x + y ) ⋅ ( x − y )
2 x + y − 23 = x + 7
Calcola:
a. il lato del rombo;
[3 13 cm]
b. il lato del quadrato equivalente al rombo;
[6 3 cm]
c. il raggio del cerchio inscritto nel rombo.
[
36 13
cm]
13
87) Un trapezio isoscele ha la base maggiore doppia della minore e gli angoli adiacenti alla base
maggiore di 45°. Sapendo che il prodotto delle misure delle due basi, espresso in cm2, è 800,
calcola:
a. la misura delle diagonali del trapezio;
[10 10 cm ; 10 10 cm]
b. il perimetro del trapezio;
c. l’area del trapezio.
(
)
[20 3 + 2 cm]
[300 cm2]
88) In un rombo ABCD, l’angolo di vertice A è di 60°. Sapendo che l’area del rombo è di
98 3
cm2, calcola:
a. la misura delle diagonali del rombo;
b. la lunghezza della circonferenza inscritta nel rombo.
[14 cm; 14 3 cm]
[7 π
3 cm]
89) Sia data una circonferenza Γ di centro O e raggio di 20 cm . Calcola:
a. il lato e l’apotema del triangolo equilatero inscritto nella circonferenza;
b. il lato e l’apotema del triangolo equilatero circoscritto alla circonferenza;
c. il lato e l’apotema del quadrato inscritto nella circonferenza;
d. il lato e l’apotema del quadrato circoscritto alla circonferenza;
e. il lato e l’apotema dell’esagono regolare inscritto nella circonferenza;
f. il lato e l’apotema dell’esagono regolare circoscritto alla circonferenza.
196
OLIMPIADI
90) Sui tre lati AB, BC, CA di un triangolo ABC si considerino rispettivamente tre punti L, M, N tali
1
1
1
che AL = LB, BM = MC, CN = NA. Qual è il rapporto fra l’area del triangolo LMN e
2
2
2
quella del triangolo ABC?
A.
1
4
B.
1
3
C.
5
12
D.
1
2
E. Dipende dal particolare triangolo considerato.
(Giochi di Archimede, triennio 1999)
[B]
91) Da una lamiera di forma quadrata si taglia un cerchio del diametro massimo possibile,
successivamente da tale cerchio si taglia un quadrato di lato massimo possibile. La percentuale di
lamiera sprecata è:
A.
1
della lamiera originale
4
B.
1
della lamiera originale
2
C.
1
della lamiera circolare
2
D.
1
della lamiera circolare
4
E. Nessuna delle precedenti
(Giochi di Archimede, biennio 1997)
[B]
197
92) Qual è la percentuale del quadrato colorata in figura?
a. 12,5%
b. 16,66%
c. 18,75%
d. 20%
e. 25%
(Giochi di Archimede, biennio e triennio 1997)
[C]
93) In un foglio a quadretti di lato
1
cm è disegnato il triangolo a fianco. Quanto vale la sua area?
2
a. 3 cm2
b. 6 cm2
c. 1,5 cm2
d. 2 cm2
e. 1 cm2
(Giochi di Archimede, biennio e triennio 1997)
[C]
94) Dato un foglio rettangolare di lati a e b, con a > b, determinare l’area dei triangolo che risulta
dalla sovrapposizione dei due lembi che si ottengono piegando il foglio lungo una diagonale (il
triangolo colorato nella figura a fianco sotto).
(Gara Nazionale 1999)
[S =
(
)
b a2 + b2
]
4a
198
95) La tela di un dipinto rettangolare è circondata da un passepartout (cioè un riquadro) largo 10 cm.
Attorno a quest’ultimo vi è poi una cornice, anche’essa larga 10 cm (nella figura, il rettangolo
bianco rappresenta la tela, la superficie tratteggiata il passepartout, la superficie nera la cornice).
Si sa che l’area dell’intero quadro (compresa la cornice) è uguale al doppio della somma di quelle
del passepartout della tela.
Si può allora concludere che:
a. sono determinate sia l’area della cornice che quelle del passepartout e della tela
b. è determinata solo l’area della cornice
c. è determinata solo l’area del passepartout
d. è determinata solo l’area della tela
e. non è determinata nessuna delle grandezze precedenti.
(Gara Provinciale 2000)
[D]
96) I tre quadrati del disegno hanno lo stesso lato. In che rapporto stanno le aree delle tre figure
colorate?
a. La prima area è maggiore delle altre due
b. La seconda area è maggiore delle altre due
c. La terza area è maggiore delle altre due
d. La prima area è uguale alla seconda, ed entrambe sono maggiori della terza
e. Le tre aree sono uguali
1
2
3
(Gara di Archimede, biennio 1996)
199