Concetti per il calcolo delle probabilità
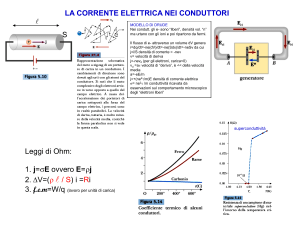
"La prova genera l 'evento con una certa probabilità".
Prova, evento, probabilità, sono concetti primitivi, nozioni intuitive.
Comunque una loro qualificazione è opportuna darla.
prova: un'esperimento soggetto a incertezza;
evento: uno dei possibili risultati della prova e costituisce un insieme di descrizioni
circa i possibili risultati dell'esperimento;
probabilità: un numero associato al presentarsi di un evento.
Gli eventi: una classificazione
Gli eventi possono essere : veri o falsi
gli eventi possono essere poi: impossibili, certi, casuali (probabili, aleatori,
possibili)
eventi certi: quando in base alle informazioni si desume che l'evento in ogni prova
assume il valore vero;
eventi impossibili: quando in base alle informazioni si deduce la falsità dell'evento;
eventi casuali: sempre in base ai dati non è possibile dedurre la verità o la falsità
dell'evento;
Ogni risultato di una prova (evento) costituisce un campione e l'insieme di tutti i
risultati (o degli eventi) possibili forma lo spazio campionario o spazio degli
eventi. Gli eventi sono, quindi, sottoinsiemi dello spazio campionario; i sottoinsiemi
con un solo elemento sono eventi elementari; i sottoinsiemi con più elementi sono
eventi composti.
Ad ogni esperimento si può associare un insieme SZ (spazio degli eventi); SZ è legato
al tipo di esperimento, non è fisso ma dipende dal problema.
=
{ l , 2,3,4, 5,6}: spazio degli eventi (spazio fondamentale) delle facce di un dado.
Siano gli eventi:
a) Numeri pari;
b) Numero 4;
C) Numeri l3;
d) Numeri > 5;
e) Tutti i numeri escluso 4 e 5 (O);
f) Complementare di O (U);
Classe degli eventi di a :
dove n è il numero degli elementi dell'insieme a , cioè, in altre parole, il numero di
sottoinsiemi che con si possono formare compreso l'insieme vuoto e lo stesso
(partizione di un insieme o insieme potenza), a secondo della struttura della prova.
*)
(i)
=
n!
= k!(n- k ) !
(combinazioni di n elementi presi k volte)
Probabilità nelllimpostazione assiornatica (Kolmogorov, 1933).
Si consideri un insieme SZ di eventi elementari, cioè lo spazio campionario.
Si definisce quindi una classe A di eventi generata a partire dagli eventi elementari di SZ,
una classe sufficientemente ampia tale da consentire operazioni logiche sui suoi elementi
senza uscire dalla classe stessa, cioè la classe A deve essere una sigma-algebra (a-algebra);
una sinma-algebra è detta anche campo degli eventi.
Per probabilizzare questi eventi si introduce la funzione P che associa un numero reale
compreso tra O e 1 ad ogni evento del campo degli eventi se sono soddisfatti i seguenti
assiomi:
U&)=flq)+fl&);
3) se El e E2 sono incompatibili, ElfìE2= 0, =>
Alcune importati proprietà per calcolo:
C) Somma di probabilità (probabilità totale): se due eventi sono non-incompatibili,
n&);
ElnE2 # 0 => fl4 uE;>=fl4>+m>-fl4
d) Prodotto di probabilità (probabilità composta):
se due eventi sono compatibili e indipendenti (v. prova)
=> qE,W)=fl4).qE;);
se gli eventi sono compatibili, ma dipendenti => fl4W)=fl&).fl&
14),
per cui
fl4 I&)= W W ),cioè la probabilità condizionata.
44)
2
u:
'Lh.
2
-
%H==
~
,
,
,@#&&@/Wdr&
cUW-
s.=~~YS,
L-4
&.e,)
mce
+-:
X -
/~l"
T
- i-
uV&<
JL A<e&%/ n = 4
m . : a,&b
;
h.
kSlr
-
&=L
*CC
3
t&**
1
2 3= g
P ( x ) :=
n!
( X !.n - x
!)
.pX,(1 - P )
n-x
F ( n ) :=
P(x)
X :=
o.. Il
n
x := O . . n
P ( x ) :=
11
n!
(x!.n- x!)
17
, p X . (1 - P )
-x
La teoria della probabilità benché sia nata per risolvere problemi dei giochi, si rivela
fondamentale per lo studio della realtà poiché ci si aspetta che quest'ultima si possa
schematizzare secondo modelli teorici riconducibili alla struttura sperimentale dei giochi.
Per questo motivo nella realtà quando si prendono delle decisioni globali, sulla base di
osservazioni parziali, si ricorre a un giudizio probabilistico di tali decisioni.
La teoria del calcolo delle probabilità riveste un ruolo incontestabile che consiste nella
costruzione dei modelli matematici per lo studio di fenomeni casuali e nello sviluppo delle
conseguenze logico-deduttive che derivano dall'applicazione di tali modelli. Così come
l'inferenza statistica costituisce il passaggio dal campione alla popolazione (processo
induttivo o problema inverso) la teoria delle probabilità affronta il passaggio dalla
popolazione ai risultati empirici o alle previsioni (processo deduttivo o problema diretto).
Va sottolineato come nella costruzione logica mediante gli assiomi la teoria delle
probabilità non si pone il problema di come si valuta la probabilità di un particolare evento.
Essa esprime piuttosto un insieme di relazioni fondamentali, di regole formali sulla base
delle quali è possibile attribuire, in modo del tutto coerente, delle probabilità a degli eventi e
non un unica probabilità. Non si pone il problema di "misurare" la probabilità degli eventi.
Infatti non viene definita nessuna funzione per il calcolo della probabilità, né appare un
valore numerico escluso i casi limiti O ed 1. In questo senso le definizioni di "probabilità
classica" e di "probabilità fì-equentista" diventano così solo dei modi possibili per attribuire
le probabilità agli eventi.
I1 calcolo basato sugli assiomi ci pone in condizioni di lavorare quando siamo in possesso
di un valore di probabilità, cioè quando si siano ricavate in qualche modo le probabilità
iniziali. Quindi la determinazione del valore di p (probabilità iniziale), e la sua valutazione,
deriverà da considerazioni analitiche o da considerazioni sull'effettuazione dell'esperimento,
oppure da informazioni sul meccanismo sottostante il fenomeno o da altri tipi di
considerazioni. I problemi relativi alla determinazione di p ricadono nell'ambito
dell'inferenza statistica.
RIFLESSIONI SULLA STATISTICA
"L'oggetto del metodo statistico è la riduzione dei dati. Una massa di dati deve essere
sostituita da un piccolo numero di quantità che rappresentano correttamente questa massa e
che devono contenere il massimo di informazione pertinente contenuta nei dati originari.
Questo obbiettivo si raggiunge con la costruzione di una popolazione infinita ipotetica. La
statistica comporta dei problemi di specificazione, che sorgono nella scelta della forma
matematica della popolazione, problemi di stima, che implicano la scelta del metodo di
calcolo delle quantità derivate dai campioni che noi chiameremo "statistiche", costruite per
stimare i valori dei parametri della popolazione ipotetica ed infine i problemi di
distribuzione". (R.Fisher (19 12), On the Mathematical Foundations of Theoretical
Statistics)
Nel caso di v. C. continue non è possibile attribuire le probabilità ai singoli valori.
Nelle v. C. discrete, in corrispondenza di ogni singolo valore, la probabilità è espressa
dall'area di un istograrnrna di ampiezza Ax e altezza A (densità di frequenza).
X
Con le v. C. continue in corrispondenza dei singoli valori non si hanno istograrnmi ma
segmenti,
quindi P(x) = O;
Di qui la necessità di introdurre una funzione matematica f(x) i cui valori non
esprimono le probabilità o le frequenze, ma conservano il significato di altezze di
rettangoli, con basi infinitamente piccole, le cui aree sono delle frequenze.
f(x) è detta funzione di densità difreguenza ed è il rapporto tra la frequenza dei
valori compresi in un intervallo infinitamente piccolo e l'ampiezza dell'intervallo
stesso. Indicando con dx l'ampiezza infinitesima dell'intervallo, la frequenza è data
dal prodotto della densità di frequenza f(x) per l'ampiezza dx, cioè
ed è una quantità infinitesima, come l'ampiezza dell'intervallo dei valori di x.
F(x) è la funzione di ripartizione e conserva lo stesso significato del caso delle V.C.
discrete, cioè la frequenza relativa (quindi la probabilità) dei valori minori o uguali ad
X
Pertanto la funzione di densità delle frequenze è data dal rapporto differenziale
cioè la funzione di densità è la derivata della funzione di ripartizione.
Con essa è possibile assegnare probabilità a singoli intervalli:
Una V.C.X continua, con valori in un certo intervallo [a, b], è definita se esiste una
funzione di densità f(x) tale che per ogni x E [a, b ]
P(x, 2 X
2 x,
+ dx) = f
(x)dx
cioè:
P(a I X Ib) =
Quindi si parla di probabilità al più per intervalli infinitesimali:
La funzione di densità deve soddisfare tali proprietà:
1) f ( x k 0 ;
,K= - - - r4
(x; -.h)
T+
m.
/&Ltic L 4
l
~ ( A n / f i ì ;