Parte quarta

Master in Analisi dei Mercati e Sviluppo Locale
Modulo di
Economia Industriale e Settoriale
Dott.ssa Marcella Scrimitore
Parte quarta
1
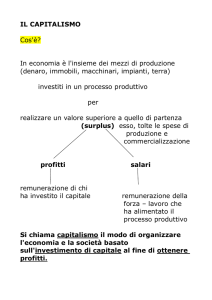
La struttura verticale dei mercati
•
•
•
Ogni settore ha una struttura verticale dalle
materie prime al prodotto finale (da ‘monte’ a
‘valle’)
La struttura verticale influenza la concorrenza
La struttura verticale varia a seconda di
decisioni istituzionali e decisioni strategiche
2
1
La struttura verticale dei mercati
•
•
•
Come una data struttura verticale influenza la
decisione finale sul prezzo
Quali inefficienze questo possa generare sui
prezzi e sui profitti
Quali tipi di contratti possono porre rimedio a
tali inefficienze?
3
Le fasi della catena del valore
•
•
•
•
Fase della produzione del bene: costo
marginale pari a c
Fase della vendita del bene: costi nulli
Prezzo finale p
Il profitto totale del settore è quindi
∏ = (p - c)q
4
2
Separazione e integrazione
5
L’impresa verticalmente integrata
•
Il profitto dell’impresa coincide con quello del
settore πI = ∏ = (p - c)q
•
Quale prezzo massimizza il profitto del settore?
Il prezzo che fisserebbe un monopolista
pI = pM
6
3
L’impresa verticalmente integrata
Si pensi a un mercato popolato da 4 individui
per i quali le disponibilità a pagare siano:
D₁=9 D₂=8 D₃=7 D₄=6
Su tale mercato le imprese sostengono un
costo per unità prodotta pari a 2.
7
L’impresa verticalmente integrata
• Fissando un prezzo pari a p = 6,
4 consumatori acquistano il bene.
I profitti saranno: πI = (6-2)4 = 16
• Fissando un prezzo pari a p = 7,
3 consumatori acquistano.
I profitti saranno: πI = (7-2)3 = 15
8
4
L’impresa verticalmente integrata
• Fissando un prezzo pari a p = 8,
2 consumatori acquistano il bene. I profitti saranno:
πI = (8-2)2 = 12
• Fissando un prezzo pari a p = 9,
solo un consumatore acquista. I profitti saranno: πI
= 9-2 = 7
⇒ Il profitto è massimo e pari a πI = 16 quando pI = 6
9
La separazione verticale
•
•
•
•
Produzione e vendita gestite da imprese
diverse
A monte, la produzione:
πP = (w - c)q (w sia il prezzo all’ingrosso)
A valle, la vendita:
πD = (p - w)q (w è in questo caso il costo
marginale; stesso valore di q in presenza di una
tecnologia 1 a 1)
Se w > c il costo marginale di chi fissa il
prezzo finale sarà più elevato
10
5
Prezzi con separazione verticale
Torniamo all’esempio precedente. Assumiamo
w > 2. Il valore dei profitti dell’impresa a valle
calcolati per un generico valore di w è:
πD = (6 - w)4 = 24 - 4w se p = 6
πD = (7 - w)3 = 21 - 3w se p = 7
πD = (8 - w)2 = 16 - 2w se p = 8
πD = 9 - w se p = 9
Se w = 6, il massimo profitto per il dettagliante si
associa a un prezzo ottimo pari a pS = 8.
11
Prezzi con separazione verticale
I profitti delle due imprese sono:
πP = (6 - 2)2 = 8
πD = (8 - 6)2 = 4
Per ogni altro valore di w i profitti del
produttore risultano inferiori. Dunque w = 6 è il
prezzo che massimizza i profitti del produttore e
pS = 8 è il prezzo che massimizza i profitti del
dettagliante.
12
6
La doppia marginalizzazione
La separazione verticale genera prezzi più
elevati rispetto a una struttura verticalmente
integrata:
pS = 8 > pI = 6
La struttura verticalmente separata riduce i
profitti complessivi del settore:
πP + πD = 12 < 16 = πI
13
La doppia marginalizzazione
•
Con separazione il prezzo di vendita è maggiore in
quanto entrambe le imprese hanno potere di mercato, e
quindi entrambe impongono un mark-up
•
Il fenomeno è noto come doppia marginalizzazione che si
genera quando è presenza di un’esternalità verticale
(l’impresa a valle non tiene conto nella sua decisione
sul prezzo finale dell’effetto che questa ha sui profitti
dell’impresa a monte)
•
In una struttura integrata tale esternalità è internalizzata
14
7
Gli effetti della separazione
sul benessere sociale
• I profitti si riducono e il surplus dei consumatori si
riduce
⇒ Il benessere complessivo W si riduce
• Struttura integrata: pI = 6; q = 4;
Π = 16; S = (9-6)+(8-6)+(7-6) = 6; W=16 + 6= 22
• Struttura separata: pS = 8; q = 2;
πP + πD = 12; S = (9-8)= 1
W=12 + 1= 13
15
Evitare la doppia marginalizzazione
• Perdita dei profitti potenziali da parte delle
imprese (Soluzione ovvia: integrazione/fusione
verticale)
•
-
Quali le cause del problema?
libertà del venditore di fissare il prezzo
struttura semplice del contratto di vendita
potere di mercato in entrambi gli stadi
16
8
Fusioni verticali
Le ragioni dell’integrazione.
• riduzione dei costi di transazione
• fornitura costante
• elusione di imposte
• eliminazione di potere di mercato di un’impresa rivale
• internalizzazione di esternalità e di free-riding in presenza di
beneficio collettivo
• acquisizione del potere di mercato
17
Restrizioni verticali
Possibili contratti attraverso i quali porre rimedio alla
doppia marginalizzazione:
• Prezzi imposti (resale price maintenance - RPM)
• Quantità imposte
• Contratti di franchising (prezzi non lineari)
Tali contratti rappresentano delle restrizioni verticali
Un altro esempio di restrizione verticale è rappresentato
dalle clausole di esclusiva (soluzione a un problema di freeriding)
18
9
Restrizioni verticali
• Attraverso il RPM: il produttore potrebbe imporre un
prezzo di rivendita ottimale
• L’imposizione di una quantità minima: il produttore
potrebbe richiedere un incremento della produzione
portandolo ad un livello ottimale
• Definizione di prezzi non lineari: il produttore stabilisce
una tassa (di franchising) pari ad F ed un prezzo variabile
pari al costo unitario di produzione che è, così, uguale a
quello ottimale. La distribuzione dei profitti dipende dal
potere contrattuale delle due imprese.
19
Restrizioni verticali
• Le clausole di esclusiva territoriale prevedono che sia un
solo rivenditore di una particolare marca in una
delimitata area territoriale
• La distribuzione in esclusiva vincola il rivenditore a
commercializzare solo la marca di un certo produttore
• Le clausole di distribuzione selettiva prevedono che la
marca di un produttore sia commercializzata da specifici
rivenditori
20
10
Fusioni verticali e restrizioni
• Le restrizioni verticali rappresentano spesso
un’alternativa alle fusioni verticali (anche se non
conducono sempre a risultati equivalenti) quando queste
sono difficili da realizzare od inefficaci
• Restrizioni e fusioni sono considerate pratiche
potenzialmente lesive della concorrenza, ma dalla nostra
analisi emergono ragioni per credere che le restrizioni
della concorrenza non sempre si associano a riduzioni
del benessere sociale!
21
Fusioni verticali e restrizioni
•
•
•
Le restrizioni verticali e, eventualmente, le
fusioni verticali possono avere effetti sulle
catene verticali concorrenti ed essere, pertanto,
utilizzate per fini strategici
In particolare, esse possono favorire la
collusione, limitando l’accesso al mercato
La fusione verticale peggiora il benessere sociale
quando porta a una chiusura del mercato
(foreclosure)
22
11
Fusioni verticali e restrizioni
• Le restrizioni e le fusioni verticali tra imprese sono molto
diffuse ed il loro effetto in termini di benessere sociale è
ambiguo. In alcuni casi possono favorire l’efficienza ed in
altri casi possono avere effetti anti-concorrenziali.
• Questa ambiguità solleva problemi importanti per
l’attività antitrust. L’attenzione dell’autorità dovrebbe
principalmente rivolgersi alle restrizioni e fusioni verticali
che interessano imprese con un elevato potere di mercato
e che, pertanto, fanno ritenere le conseguenze anticoncorrenziali rilevanti.
23
Fusioni orizzontali
• Le imprese possono incrementare il potere di
mercato attuando una fusione:
- orizzontale, quando coinvolge imprese che
operano nella stessa fase del ciclo produttivo
- conglomerale, quando coinvolge imprese che
operano in filiere diverse
24
12
Fusioni orizzontali
In generale, un’operazione di concentrazione è
vietata quando determina la costituzione o il
rafforzamento di una posizione dominante
nei mercati interessati tale da eliminare o
ridurre in modo sostanziale e durevole la
concorrenza
25
Fusioni e incentivi privati
Assumiamo che ci siano tre imprese
qi = 48
p = 28; πi (3) = 1152
Se due imprese si fondono la fusione non è
profittevole. Infatti: qi = 64 e p = 36; πi (2)= 2048
dunque ciascuna impresa ottiene:
πi (2)/2 = 2048/2 < πi (3)= 1152
26
13
Fusioni e incentivi privati
• Lasciamo invariati i dati dell’esercizio precedente e
aggiungiamo un costo fisso F: qi = 48; p = 28
I profitti saranno: πi (3) = 1152 – F
• La fusione diventa profittevole per livelli del costo
fisso sufficientemente elevati: πi (2) = 2048 – F
πi (2)/2= (2048 – F)/2 > πi (3)= 1152 – F
che si verifica quando F > 256
27
Fusioni e incentivi privati
• I costi fissi si ripartiscono in seguito alla
fusione generando delle economie di scala
• Tali economie di scala rappresentano i
vantaggi di costo che rendono profittevole
l’operazione rispetto agli obiettivi delle
imprese e a cui si associa una maggiore
efficienza a livello collettivo
28
14
Fusioni e incentivi privati
• E’evidente che le economie di scala devono essere
sufficientemente rilevanti perchè ciò si realizzi
(valore di F sufficientemente elevato)
• A un’operazione di concentrazione si associano
dunque effetti anti-competitivi (maggior potere di
mercato) e pro-competitivi (vantaggi di costo)
• N.B. E’ possibile riscontrare vantaggi di costo anche
quando siano presenti economie di varietà o un
elevato grado di eterogeneità delle imprese
29
Fusioni e incentivi sociali
Il benessere prima della fusione:
W (3) = S(3) + 3πi(3)
Il benessere post-fusione: W‘ (2) = S(2) + 2πi(2)
La fusione è ritenuta socialmente desiderabile se
W’ (2) > W (3), che nel caso specifico
equivale a:
8192-2F > 8640-3F
che si verifica quando F > 448
30
15
Fusioni e incentivi sociali
• L’intervallo dei costi fissi entro il quale la fusione è
socialmente desiderabile è un sottoinsieme
dell’intervallo dell’intervallo entro il quale la fusione è
profittevole per le imprese
• Questo equivale a dire che esistono situazioni in cui gli
incentivi privati generano esiti non desiderabili dal
punto visto sociale
• Sono queste le situazioni dannose per la società che
devono essere correttamente individuate e vietate
31
16