I TRIANGOLI
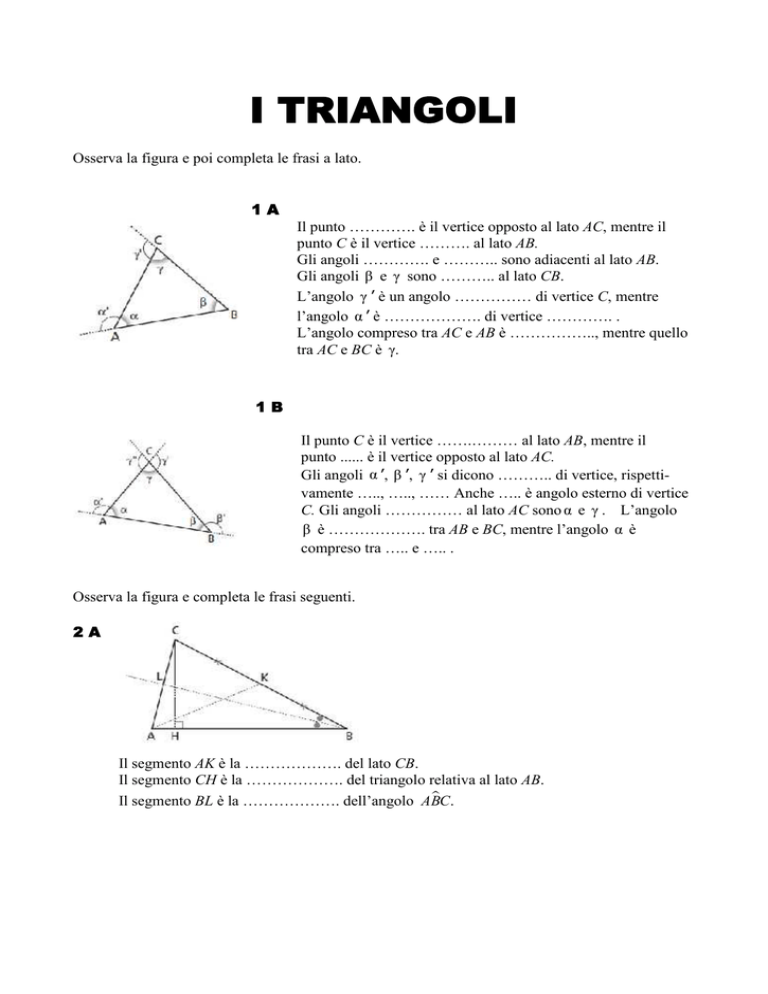
Osserva la figura e poi completa le frasi a lato.
1A
Il punto …………. è il vertice opposto al lato AC, mentre il
punto C è il vertice ………. al lato AB.
Gli angoli …………. e ……….. sono adiacenti al lato AB.
Gli angoli β e γ sono ……….. al lato CB.
L’angolo γ ’ è un angolo …………… di vertice C, mentre
l’angolo α ’ è ………………. di vertice …………. .
L’angolo compreso tra AC e AB è …………….., mentre quello
tra AC e BC è γ.
1B
Il punto C è il vertice …….……… al lato AB, mentre il
punto ...... è il vertice opposto al lato AC.
Gli angoli α ’, β ’, γ ’ si dicono ……….. di vertice, rispettivamente ….., ….., …… Anche ….. è angolo esterno di vertice
C. Gli angoli …………… al lato AC sono α e γ . L’angolo
β è ………………. tra AB e BC, mentre l’angolo α è
compreso tra ….. e ….. .
Osserva la figura e completa le frasi seguenti.
2A
Il segmento AK è la ………………. del lato CB.
Il segmento CH è la ………………. del triangolo relativa al lato AB.
.
Il segmento BL è la ………………. dell’angolo ABC
2B
Il segmento BQ è la ………………. del lato AC.
Il segmento BK è la ………………. del triangolo relativa al lato AC.
Il segmento AS è la ………………. dell’angolo C
AB.
Rappresenta la figura e scrivi l’ipotesi e la tesi del seguente teorema.
5A
È dato un triangolo isoscele ABC di base AB. Tracciata l’altezza CH, prolungala di un
segmento CD, esternamente al triangolo, in modo che CD CH . Congiungi D con A e B.
Dimostra che il triangolo ABD è isoscele.
5B
È dato un triangolo isoscele ABC di base BC. Tracciata l’altezza AH, prolungala di un
segmento AD, esternamente al triangolo, dalla parte di BC, in modo che AD AH .
Congiungi D con B e C. Dimostra che il triangolo BCD è isoscele.
Disegna un triangolo ABC. Dalla parte di A prolunga il lato AC di un segmento AD AC e
il lato AB di un segmento AE AB. Dimostra che i triangoli ABD e ACE sono congruenti.
6A
11 A Dato un triangolo isoscele ABC di base AB, traccia le bisettrici relative ai vertici A e B che
incontrano i lati BC e AC rispettivamente nei punti E e D. Prolunga le bisettrici di due
segmenti congruenti DF ed EG. Congiungi F con A e G con B. Dimostra che AF BG.
11 B Dato un triangolo isoscele ABC di base BC, traccia le bisettrici relative ai vertici B e C che
incontrano i lati AC e AB rispettivamente nei punti M e N. Prolunga le bisettrici di due
segmenti congruenti BP e CQ. Congiungi C con P e B con Q. Dimostra che BQ CP.
15 A Disegna il triangolo isoscele ABC di base AB. Esternamente al triangolo prendi un punto D
in modo che DA DB. Unisci D con A, con B e con C e dimostra che i triangoli DAC e
DBC sono congruenti.
Prova a riprodurre le figure descritte nei problemi 11A, 11B e15A con Geogebra, salva il file con
nome corrispondente al numero dell’esercizio ed invialo sul forum.
COMPITI 1As 12/2012
1
Posto X 3 x y, Y y 2 x 2 , Z 2 xy , semplifica la seguente espressione.
2
9 3
39 2
2
3
31 A X Z 3Y 2 XZ
15 xy 2 x 3 y 2 x y
6 xy 2 3 x 3 2 y 3 x 2 y
31 B X 2Y Z XZ
3
4
della base maggiore, mentre l’altezza è il doppio della base minore. Esprimi con un
polinomio ridotto la misura del perimetro e dell’area del trapezio.
7
15
2
2 x 2 y; 2 y 3 xy
Esprimi mediante un polinomio ridotto a forma normale il perimetro e l’area della zona evidenziata.
32 B In un trapezio isoscele la base maggiore supera di 3x la base minore y, il lato obliquo è
33 A
4a 8c; a 2 2b 2 4ab c 2
33 B
18a 2c; 12a 2 bc
2
3 3
2
1
42 A a b b a a b 3 2a a b
2 2
3
2
42 B
43 2 9 2
12 b 4 a
2
1
1
2 8
2
x y 2x x y x y y x x2
2
3 3
3
3
2
1 2 4
2 y 3 xy
3 4
3
4
2 a a b
2
1
3
b 4 3 a b 1 b 1 a 2 b 2
2
2
1
2
3
1
43 B 12a a b a b b b 2a 2a 4a 2b 2a b
2
2
43 A
44 A
44 B
a b
2 3
x 3x 2 x x 2 x 3 2 x x 1 x x 10
a 2 a 3a 1 a a a 2 a 3 a 2a 3 a a
2
2
2
3
2
3
2
14a 3
2
2
2
3
2a 2 13
x 2 4
4a 2 9
Esegui le divisioni applicando la regola di Ruffini.
5
3
57 A 4 y 4 y 2 9 y 9 : y
4
4
4
5
2
57 B a 4 a 1 a 3 : a
9
3
3
58 A
58 B
7 b b
6 a 5a
3
4
2
3
2b 4 4b 3 : 2b 1
23a 2 20a 4 : 3a 1
59 A 15 x 5 y 9 x 2 y 2 6 xy : y 3x
59 B
a
3
39
27
3
2
Q 4 y 3 y y 4 ; R 16
2
3
2
Q a a 3 a; R 1
Q b3 3b 2 2b 1; R 2
4a 2b a 3ab 2 3b : a 3b
Q 2a 3 a 2 8a 4; R 0
x
a
Q 3 x 5 y; R 0
Q a 2 ab 1; R 0
Stabilisci se il polinomio assegnato è divisibile per ciascuno dei binomi scritti a lato
5
1
62 A 12a 4 a ;
[no; no; no; no]
2a 1, a 1, a 2, a .
3
3
1
62 B 36 x 4 13x 2 1;
[sì; no; no; no]
3 x 1, x 1, x 2, x .
4
.
Gli esercizi svolti saranno ricopiati su foglio da compito in classe e
consegnati al rientro dalla vacanze.












