Sezione Aurea o Numero Aureo o Rapporto Aureo
E’ un numero decimale infinito non periodico, indicato con la lettera
greca ɸ (si legge “fi”), che arrotondato al centesimo è 1,62.
ɸ= 1,61803398874989484820458683436..
Fu introdotto dai Pitagorici nel VI secolo e utilizzato per COSTRUIRE FORME
“PERFETTE” , qualcosa di veramente “bello”.
Fu adottato nella Scultura, nella Pittura, nell’Architettura, nella Matematica e
nella Geometria ma soprattutto si è constatato che era presente in Natura, in
Anatomia e in Astronomia.
Moltissimi artisti rinascimentali, tra i quali Leonardo da Vinci, si dedicarono allo studio
delle proporzioni ARMONICHE ; esprimendo il rapporto armonico delle singole parti di una
figura con il tutto, per conseguire un ideale di bellezza.
Lo Scultore greco Policleto il Vecchio:
“..La figura umana deve essere salda, atletica, armoniosa, con la testa
piccola e la fronte larga, la metà del corpo deve essere nell’attacco delle
gambe, il piede è un settimo della lunghezza del corpo, la testa
un’ottavo, e la faccia un decimo..”.
Nel Libro Terzo del trattato De architectura scritto da Vitruvio :
“.. Il centro naturale del corpo umano è l’ombelico; infatti, se una
persona si distendesse a terra supina a braccia e gambe divaricate,
puntando il compasso sull’ombelico e tracciando una circonferenza,
questa toccherebbe entrambe le estremità dei piedi e delle mani.
Nondimeno, com’è possibile inscrivere il corpo in una circonferenza così
se ne può ricavare un quadrato; misurando la distanza dai piedi alla
sommità del capo e riportandola a quella che intercorre tra un estremo e
l’altro delle braccia aperte si costaterà che le misure in altezza e
larghezza coincidono come nel quadrato tracciato a squadra.”
Le proporzioni
del corpo
umano secondo
Vitruvio
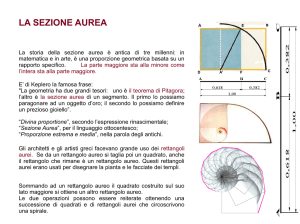
Famosa è la rappresentazione di Leonardo
dell'uomo di Vitruvio in cui un uomo è inscritto
in un quadrato e in un cerchio.
Nel quadrato, l'altezza dell'uomo (AB) è pari alla
distanza (BC) tra le estremità delle mani con le
braccia distese.
La retta x-y passante per l'ombelico divide i lati
AB e CD esattamente in rapporto aureo tra loro.
Lo stesso ombelico è anche il centro del cerchio
che inscrive la persona umana con le braccia e
gambe aperte.
La posizione corrispondente all'ombelico è
infatti ritenuta il baricentro del corpo umano.
Diversi dipinti sono stati composti secondo la sezione aurea
Una famosa rappresentazione della figura umana in
proporzioni auree è anche la Venere di Botticelli
Oltre all’altezza da terra dell’ombelico e l’altezza
complessiva, è aureo anche il rapporto tra la
distanza del collo del femore al ginocchio e la
lunghezza dell’intera gamba o il rapporto tra il
gomito e la punta del dito medio e la lunghezza
dell'intero braccio.
a
ɸ = a: b = 1,62 più vicino sei a questa misura più sei BELLO/A…
Ma NON ti preoccupare l’importante è essere BELLI DENTRO…
non basta fare un calcolo!
Le proporzioni del viso: a = distanza dalla nuca al mento
b = distanza da un orecchio all’altro
Le proporzioni delle gambe: a = distanza dall’anca al piede
b = distanza dal ginocchio al piede
Le proporzioni del corpo: a =distanza dalla testa ai piedi
b= distanza dall’ombelico ai piedi
b
Edifici, giardini e monumenti sono stati progettati con rettangoli
aurei (il Partenone di Atene, la Grande Piramide a Giza o il palazzo
di vetro dell’ONU), così pure le comuni CARTE di CREDITO
b
a
Il Rettangolo è Aureo se
a : b=1,62
Per la sua Costruzione si
parte da un quadrato
Molte opere di artisti, da Leonardo da Vinci a Piero della Francesca, da Sandro
Botticelli a Salvador Dalì, sono strutturate secondo una griglia di rettangoli aurei.
La "Belle Ferronnière"
a
b
b
a
L'Annunciazione, di Piero della Francesca,
Molti esseri viventi hanno spesso proporzioni basate sul rettangolo aureo.
b
La spirale logaritmica
detta anche "spirale
aurea", ritrovata nelle
Ammoniti, nel Nautilo
e nei foraminiferi.
a
Esprime il modo di accrescere "secondo natura“
in maniera ottimale e meno dispendiosa possibile.
Anche la Via
Lattea é una
spirale aurea
In un ciclone i venti
descrivono spirali quasi
perfette,
antiorarie
nell’emisfero boreale e
orarie in quelle australi.
I pistilli sulle corolle spesso sono messi secondo uno
schema preciso formato da spirali in modo da essere
uniformemente sparsi su tutta la corolla e non troppo
ammassati al centro.
Le brattee delle pigne si dispongono in due
serie di spirali dal ramo verso l'esterno
Abbiamo visto come la natura ha saputo sfruttare le rigide leggi
matematiche e geometriche per raggiungere un equilibrio e una
armonia che noi dobbiamo rispettare e conservare.
Se l’uomo fa proprie le Leggi della Natura, la Natura rispetterà l’uomo.
I Pitagorici trovarono la sezione Aurea nel loro simbolo:
il PENTACOLO
Cioè la stella a cinque punte inscritta in un pentagono regolare o un
circonferenza.
La configurazione di pentagoni si presta a scoperte meravigliose
dove è possibile incontrare il numero d’oro a ogni passo.
http://www.astronomyproject.com/2011/05/06/sezione-aurea-paperino-e-astronomia/
Essa compare anche in molti poligoni
regolari e poliedri regolari ed archimedei.
Ecco alcuni esempi:
i poliedri disegnati da Leonardo da Vinci
dodecaedro
pentagonale
Anche la complessa geometria che sottende
alla creazione di un carattere tipografico si
attiene alle proporzioni AUREE
La lettera A da “de divina proportione”
di Luca Pacioli (Venezia 1509)
Esiste una Relazione tra NUMERO AUREO e la successione di FIBONACCI (Leonardo
Pisano 1170-1250, detto Fibonacci perché figlio di Bonaccio un mercante di Pisa).
Quante coppie di conigli verranno prodotte in un anno, a partire da un’unica coppia, se
ogni mese ciascuna coppia dà alla luce una nuova coppia che diventa produttiva a partire
dal secondo mese? (“tratto da Liber abaci”)
Questo problema origina la “Serie di Fibonacci”:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ….,
dove ciascun termine dopo i primi due è la somma dei due termini precedenti.
Esiste una stretta relazione tra questi numeri e il numero Aureo ɸ, infatti se n
diventa molto grande il rapporto fra due termini successivi è il numero aureo.
Le scaglie degli ananas presentano un'aderenza costante ai fenomeni di Fibonacci.
• DALLE FORBICI AL COMPUTER (Laboratorio delle competenze)
Ed. Bruno Mondadori autori: M.Zarattini e L.Aicardi
• Cit. da Marco Vitruvio Pollione, De Architectura Libri X, trad. di
L.Migotto, StudioTesi, Pordenone 1990, pag. 127
• Cit. da Progetto realizzato da IIS “Maserati” - sezione associata
“Baratta” Classe 3BG Docenti: Prof.Donatella Cabrini
Prof.Antonella Dabusti Prof. Maria Lagomarsini