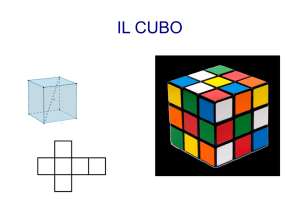
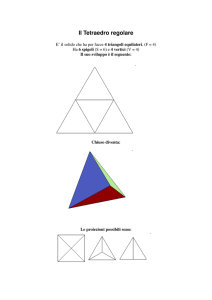
Angoli e poligoni regolari
Ci serviranno bastoncini blu e qualche pallina.
9 Le palline hanno buchi a forma di triangolo, di rettangolo e di pentagono.
Guardiamo attraverso un foro, la faccia opposta ha la stessa forma.
9 Appoggiamo una pallina con un buco pentagonale verso l’alto e
inseriamo 10 bastoncini blu di lunghezza media come nella figura.
?1 Qual è l’angolo tra due bastoncini blu consecutivi?
9 Aggiungiamo una pallina in ogni punta libera e uniamole con 10 pezzi blu corti.
Abbiamo costruito il decagono regolare.
9 Ripetiamo l’attività appoggiando la pallina sul tavolo con un foro triangolare verso
l’alto e poi con un foro rettangolare.
Dobbiamo ottenere le stelle di 6 e 4 punte come in figura.
?2 Quanto misurano ora gli angoli tra i bastoncini blu?
9 Ecco tutti i poligoni regolari che si possono realizzare con questo materiale.
Spunti per un laboratorio di geometria, scheda 1
Prismi, antiprismi, piramidi
Ci serviranno i poligoni costruiti con la scheda precedente, molte palline, i bastoncini
gialli e quelli rossi.
9 Prendiamo un pentagono regolare di bastoncini blu medi e inseriamo 5 bastoncini rossi della
stessa lunghezza nel buco superiore della pallina. Ora costruiamo un altro pentagono come
base superiore.
9 Il nostro prisma pentagonale retto ha la base superiore e quella inferiore della stessa forma e tanti rettangoli laterali
quanti sono i lati del poligono di base. Proviamo a costruire prismi retti con altre figure alla base: triangolo, esagono,
decagono.
?1 Quale solido troviamo creando un prisma retto con le basi quadrate e tutti i lati della stessa misura?
9 Un antiprisma ha le 2 basi uguali, ma a differenza del prisma le facce laterali sono
triangoli, non rettangoli.
?2 Costruisci un antiprisma pentagonale diverso da quello del tuo vicino di banco:
puoi cambiare il colore dello zig-zag. Riesci a realizzarli tutti e 5?
9 Se prendiamo un quadrato, 4 bastoncini gialli e una pallina realizziamo una piramide,
proprio come quelle degli egizi! Proviamo a creare piramidi con basi di altre forme.
?3 Quante piramidi diverse riesci a costruire con una base triangolare? Quante con una
base pentagonale? Quando pensi di averle trovate tutte, prova a girare la figura di base sotto sopra!
Spunti per un laboratorio di geometria, scheda 2
Solidi platonici I
Costruiremo i 5 poliedri regolari: cubo, icosaedro, dodecaedro, tetraedro, ottaedro.
9 Abbiamo già costruito il cubo nella scheda 2, dove era presentato come il
prisma retto a base quadrata.
?1 Quanti lati ha ciascuna faccia? Quante facce s’incontrano in
ciascun vertice?
9 Prendiamo una pallina e infiliamo bastoncini rossi in tutti i buchi a forma
di pentagono.
9 Aggiungiamo 12 palline alle estremità libere e uniamole con 30 bastoncini blu. Le linee blu
formano l’icosaedro regolare.
?2 Quanti lati ha ciascuna faccia? Quante facce s’incontrano in ciascun vertice?
9 Ora infiliamo in una pallina bastoncini gialli medi o lunghi in tutti i buchi di forma
triangolare.
9 Inseriamo 20 palline e terminiamo con 30 bastoncini blu. Questi ultimi sono gli spigoli del
dodecaedro regolare.
?3 Quanti lati ha ciascuna faccia? Quante facce s’incontrano in ciascun vertice?
Spunti per un laboratorio di geometria, scheda 3
Solidi platonici II
Per costruire i 2 solidi platonici mancanti ci serviranno i bastoncini verdi.
9 I pezzi verdi sono le diagonali di un quadrato costruito con i lati blu.
9 Su questa base costruiamo un cubo come nella figura a lato.
9 Ora è sufficiente aggiungere una diagonale verde nelle restanti 5 facce del cubo. I
bastoncini verdi sono gli spigoli di un tetraedro regolare.
?1 Quanti lati ha ciascuna faccia? Quante facce s’incontrano
in ciascun vertice?
9 Si può ottenere un tetraedro regolare anche usando
un’impalcatura interna di bastoncini gialli come in figura.
9 Inseriamo 6 bastoncini blu in una pallina per formare 3 linee che
s’incontrano a 90 gradi come nella prima fotografia in alto a
destra.
9 Aggiungiamo una pallina a ogni estremità e terminiamo
l’ottaedro regolare con le 12 diagonali verdi.
?2 Quanti lati ha ciascuna faccia? Quante facce s’incontrano in ciascun vertice?
9 Se non hai i bastoncini verdi, puoi realizzare delle ottime
approssimazioni con i bastoncini blu e rossi, come nella
fotografia a lato. Per il tetraedro sono necessari tre bastoncini
blu e tre rossi, per l’ottaedro sei blu e sei rossi.
?1
Spunti per un laboratorio di geometria, scheda 4
Solidi platonici III
Completa una tabella come questa con tutte le informazioni riguardo ai solidi platonici.
Poliedro
Lati di ogni faccia Facce in ogni vertice Facce Vertici Spigoli
tetraedro
cubo
4
3
ottaedro
dodecaedro
icosaedro
?2 Osservando la tabella nota che il dodecaedro e l’icosaedro hanno qualcosa in comune. Trova l’altra coppia di poliedri
con caratteristiche simili. Un solido rimane da solo, come dovrebbe essere fatto il suo compagno?
9
Per provare che ci sono esattamente 5 possibilità, ragioniamo sulla somma degli angoli a ogni vertice e esaminiamo le
prime due colonne della tabella. La notazione {p, q} indica un poliedro in cui in ogni vertice s’incontrano q facce di p
lati. La notazione {4,3} si riferisce al cubo.
?3
Spiega il motivo per cui nella prima e nella seconda colonna non posso scrivere un numero minore di 3.
?4 La coppia {3,6} non si riferisce a nessun poliedro. Spiega perché.
?5 Spiega perché non esistono i poliedri {3,7}, {3,8}, {3,9}, 4,4}, {4,5}, {4,6}, {5,4}, {5,5}, {5,6} e così via.
?6 Perché nella prima colonna non posso scrivere un numero maggiore o uguale a 6?
Spunti per un laboratorio di geometria, scheda 5
Approfondimento: simmetrie dei solidi platonici I
Simmetrie dell’icosaedro regolare e del dodecaedro regolare.
Prendiamo un icosaedro regolare e aggiungiamo 2 bastoncini rossi in 2 vertici opposti come in
figura, così potremo farlo ruotare intorno a quest’asse.
9 La linea immaginaria che passa per due vertici opposti nell’icosaedro è un asse di simmetria
rotazionale di ordine 5, cioè se facciamo ruotare il solido di un quinto dell’angolo giro, tenendo
fermi i vertici, il poliedro appare come nella posizione iniziale. Lo stesso se lo muoviamo di due
quinti, di tre quinti, ecc. A ogni rotazione i vertici del solido si scambiano di posto, tranne i due
per cui passa l’asse si simmetria. Dopo cinque rotazioni torna esattamente al punto di partenza.
9 Abbiamo trovato un tipo di asse di simmetria per l’icosaedro, ma ce ne sono altri due: l’asse di simmetria di ordine tre e
quello di ordine due. Nell’icosaedro gli assi di simmetria di ordine tre passano per il centro di due facce opposte, mentre
la linea immaginaria che unisce i punti medi di due lati opposti è un asse di simmetria di ordine due.
9 Osserviamo che tutti questi assi passano per il centro del poliedro e non sono presenti assi di simmetria rotazionale di
altri tipi, ad esempio di ordine 4, o 6.
?1 Quanti assi di simmetria di ordine 2, 3, 5 ci sono in un icosaedro?
?2 Se si moltiplica il numero di assi di simmetria per il loro ordine, si ottiene sempre lo stesso numero, quale?
?3 Tutte le linee che passano per il centro sono assi di simmetria di ordine 1: vero o falso?
9 Immagina un piano che taglia a metà l’icosaedro, questo è un piano di simmetria.
?4 Quanti piani di simmetria ci sono in un icosaedro?
9 Ora prendiamo un dodecaedro regolare, facendolo ruotare lentamente cerchiamo gli assi di
simmetria.
?5 Quanti e quali assi di simmetria di ordine 2, 3, 5 ci sono in un dodecaedro? Quanti
piani di simmetria?
9 Poiché icosaedro e dodecaedro hanno tutte questa caratteristica in comune, l’insieme di tutte
le loro simmetrie è detto simmetria icosaedrale.
?6 Usando una pallina crea un modello per la simmetria icosaedrale.
Spunti per un laboratorio di geometria, scheda 6
Approfondimento: simmetrie dei solidi platonici II
L’icosaedro e il dodecaedro hanno la stessa simmetria.
Quali altri due solidi hanno una simmetria comune?
9 Osserviamo attentamente un cubo e individuiamo assi e piani di simmetria. Ignora che in un
quadrato costruito con i bastoncini blu le sezioni rettangolari sono in due direzioni diverse
tra loro perpendicolari, immagina siano rotonde.
?1 Quanti assi di simmetria di ordine 2, 3, 4 ha il cubo? Quanti piani di simmetria?
9 Esploriamo ora le simmetrie di un ottaedro regolare.
?2 Metti a confronto le simmetrie del cubo con
quelle dell’ottaedro.
9 Riprendi la costruzione del tetraedro
regolare inscritto nel cubo (il tetraedro è formato dalle diagonali verdi di un
cubo blu).
?3 In che modo sono legati gli assi e i piani di simmetria del cubo con
quelli del tetraedro?
?4
Spunti per un laboratorio di geometria, scheda 7
Approfondimento: dualità dei solidi platonici
Dato un solido platonico, ne realizzeremo un secondo in modo che i vertici di quest’ultimo siano collocati al centro delle facce
del primo.
9 Costruiamo un cubo con ogni spigolo formato da due bastoncini blu della stessa
lunghezza. Immaginiamo una sfera dentro il cubo che sfiori i punti medi di tutti gli
spigoli (le palline al centro di ogni lato). Per costruire il solido duale del cubo è
necessario inserire bastoncini perpendicolari ai suoi spigoli, tangenti la sfera.
?1 Qual è il duale del cubo?
?2 Qual è il duale dell’ottaedro?
9 Costruendo la composizione del cubo e dell’ottaedro in
posizione duale, possiamo fare alcune osservazioni:
ricordiamo che entrambi i solidi hanno 12 spigoli, non è una
coincidenza, ma una conseguenza della loro dualità.
?3 Quali relazioni possiamo dedurre per il numero di facce e
vertici dei due poliedri?
9 Il dodecaedro e l’icosaedro hanno entrambi 30 spigoli.
Controlliamo se sono duali realizzando una composizione dei due
solidi in cui gli spigoli s’intersechino ad angolo retto.
?4 Quali relazioni possiamo dedurre per il numero di facce e
vertici dei due poliedri?
?5 Se un poliedro ha k vertici, m facce e n spigoli, cosa
possiamo dire del suo duale?
?6 Qual è il duale del tetraedro regolare?
Spunti per un laboratorio di geometria, scheda 8
Approfondimento: costruzioni legate ai solidi platonici I
Realizzeremo un dodecaedro regolare a partire da un cubo.
9 Gli antichi greci scoprirono il cubo nel dodecaedro più di 2000 anni fa. Euclide notò che si può
ottenere un dodecaedro regolare aggiungendo un tetto su ogni faccia del cubo, come in figura.
Iniziamo con un cubo di bastoncini blu medi (o lunghi). Il tetto è composto da 5 bastoncini blu corti
(o medi) che formano 2 triangoli e 2 trapezi isosceli.
?1 Quanti sono gli spigoli del cubo? Quante le facce del dodecaedro? E’ una coincidenza?
9 Costruendo il dodecaedro abbiamo trovato 6 quadrati i cui vertici sono gli stessi del cubo.
?2 Quanti quadrati diversi otteniamo in questo modo?
9 Inserire tutti questi quadrati all’interno del dodecaedro può essere difficile: dovremmo
introdurre altre diagonali in ogni faccia del solido, fino a ottenere una stella con cinque punte
nel pentagono, come nella figura in basso.
9 Creiamo allora i 5 cubi nel dodecaedro a partire dalla stella nel pentagono: formiamo un
pentagono con i bastoncini blu lunghi e le diagonali con 10 bastoncini blu medi e 5
corti. Ripetiamo la stessa costruzione per le altre 11 facce del dodecaedro. Rimuovendo
delicatamente tutti gli spigoli del dodecaedro rimane una composizione di 5 cubi che
s’intersecano.
?3 Questi cubi e il dodecaedro condividono qualche asse di simmetria?
Spunti per un laboratorio di geometria, scheda 9
Approfondimento: costruzioni legate ai solidi platonici II
Realizzeremo una combinazione di 5 tetraedri concentrici in un dodecaedro e il duale di un cubo in un dodecaedro.
9 Creiamo un tetraedro regolare in un cubo utilizzando i bastoncini verdi.
9 Costruiamo un tetraedro regolare in un dodecaedro.
9 Inseriamo 5 tetraedri in un dodecaedro. Quando il modello sarà completo, potremo togliere lo
scheletro esterno blu, eccetto una faccia pentagonale che farà da base per la nostra
composizione di 5 tetraedri concentrici.
?1 In quanti modi differenti possiamo inscrivere 5 tetraedri in un dodecaedro?
9 Il duale di un cubo inscritto in un dodecaedro, è un solido formato da un icosaedro in un
dodecaedro. Realizziamolo a partire da un icosaedro regolare con gli spigoli formati da due
bastoncini blu corti.
9 Appoggiando l’icosaedro su uno spigolo individuiamo 6 dei suoi spigoli perpendicolari tra di
loro e inseriamo nel loro punto medio un bastoncino blu corto come in figura. A questi cateti
uniamo un’ipotenusa: un bastoncino verde piccolo ed estendiamo questi spigoli in un ottaedro
regolare aggiungendo bastoncini verdi lunghi. Infine si possono rimuovere i sei bastoncini blu
che ci sono serviti solo come
scaffalatura.
?2 Seguendo lo stesso
metodo quanti ottaedri
regolari possono essere
costruiti sullo stesso
icosaedro?
Spunti per un laboratorio di geometria, scheda 10
Approfondimento: costruzioni legate ai solidi platonici III
9 Costruiamo un dodecaedro regolare con i bastoncini blu corti (o medi). Ora innalziamo
una piramide retta su ogni faccia pentagonale con 5 bastoncini blu medi (o lunghi).
Otteniamo un poliedro non convesso, chiamato piccolo dodecaedro stellato.
?1 Qual è la forma delle facce di questo nuovo poliedro?
?2 Scrivi il numero di facce, vertici e spigoli del piccolo dodecaedro stellato.
9 Creiamo un icosaedro regolare con i bastoncini blu medi (o lunghi). Ora innalziamo una piccola piramide retta su ogni
faccia pentagonale con 5 bastoncini rossi corti (o medi). Rimuovendo delicatamente tutti i bastoncini blu otteniamo il
triacontaedro rombico.
?3 Qual è la forma delle facce di questo nuovo poliedro?
?4 Scrivi il numero di facce, vertici e spigoli del triacontaedro rombico.
9 Creiamo un dodecaedro regolare e innalziamo una piccola piramide rossa su ogni faccia. Rimuoviamo delicatamente
tutti i bastoncini blu.
?5 Quale solido otteniamo?
Spunti per un laboratorio di geometria, scheda 11
Approfondimento: costruzioni legate ai solidi platonici IV
9 Riprendiamo la costruzione di un tetraedro regolare in un cubo utilizzando i bastoncini verdi.
9 Il tetraedro usa solo metà degli 8 vertici del cubo. Se usassimo i vertici rimasti potremmo
costruire un secondo tetraedro. Per far questo realizziamo un cubo in doppia scala, cioè con gli
spigoli formati da due bastoncini blu della stessa lunghezza e aggiungiamo tutte le diagonali
verdi, creando delle grosse X in tutte le facce del cubo.
?1 Guardiamo attentamente i due tetraedri: come s’intersecano i loro spigoli?
9 Se rimuoviamo con delicatezza il cubo blu rimane una composizione di due tetraedri, chiamata
stella octangula, cioè stella con otto punte. (Puoi creare un piccolo treppiede rosso alla base
come in figura per farlo rimanere in piedi su un vertice).
?2 Che forma ha l’intersezione tra i due tetraedri?
9 Uniamo i punti d’intersezione con 12 bastoncini verdi. Ora possiamo vedere questa
costruzione come un poliedro che conosciamo circondato da altri piccoli solidi
?3 Descrivi questa composizione.
9 Togliamo quattro piccole piramidi in modo da lasciare un unico grande tetraedro. Il solido così
composto ci mostra come un tetraedro può essere diviso in un ottaedro e 4 piccoli tetraedri.
Spunti per un laboratorio di geometria, scheda 12
Approfondimento: solidi platonici e origami I
Costruzione del cubo:
realizza il modulo seguendo le indicazioni, a partire da un foglio rettangolare 1 x 2
Simboli
1
2
3
4
piega ancora a metà
piega a metà
e riapri
esegui le
pieghe e riapri
5
6
piega
piega e riapri
traccia della
piega eseguita
piega a metà e riapri
esegui le
pieghe e riapri
modulo
terminato
Unisci 3 moduli:
chiudere il primo modulo
chiudere il secondo e il terzo insieme
aggiungere il primo
Spunti per un laboratorio di geometria, scheda 13
cubo terminato
Approfondimento: solidi platonici e origami II
Costruzione del tetraedro:
I
realizza il modulo
destro seguendo le indicazioni, a partire da un foglio quadrato
1
3
2
esegui le pieghe che
dividono il foglio in quarti e
riapri
8
7
piega lungo la linea
tratteggiata
apri tutto
per ottenere un
per ottenere
modulo
sinistroun
modulo
eseguire
9 esinistro
10 sugli
eseguire
9 e 10 sugli
altri
due vertici
altri due vertici
esegui le pieghe
indicate e riapri
esegui le due pieghe
indicate
5
4
unisci i due punti ottieni questa
evidenziati e
figura, ora
riapri
10
9
piega lungo le due
linee tratteggiate
piega per ottenere la
figura 11
unire modulo destro e sinistro e
chiudere il tetraedro inserendo
ogni punta rosa in una tasca
azzurra e viceversa :
Spunti per un laboratorio di geometria, scheda 14
6
ripeti per gli
altri 4 vertici
11
modulo destro
terminato
Approfondimento: solidi platonici e origami III
Costruzione dell’ottaedro:
realizza 2 moduli destri e 2 sinistri come quelli del tetraedro.
i moduli azzurri sono i destri e
quelli rosa i sinistri
unisci i moduli dello stesso colore
chiudili a forma di piramide
sovrapponile e ottieni
un ottaedro
Costruzione dell’icosaedro:
realizza 5 moduli destri e 5 sinistri come quelli del tetraedro.
tieni separati i moduli destri da quelli sinistri
unisci i 5 moduli sinistri e
fai lo stesso con quelli destri
chiudili a forma di piramide,
può essere utile per il
momento usare delle clips
Spunti per un laboratorio di geometria, scheda 15
unisci le due piramidi, ora
puoi togliere le clips
Approfondimento: solidi platonici e origami IV
Costruzione del dodecaedro:
realizza il modulo a partire da un foglio rettangolare 1 x
2
1
(come quelli della fotocopiatrice)
4
3
ripeti per i vertici superiori
esegui le pieghe indicate e
riapri
sovrapponi il vertice al
centro del rettangolo
fai lo stesso con il
vertice di sinistra
5
6
piega lungo le linee tratteggiate
piega il modulo a metà per
ottenere la figura 6
e poi tutti gli altri
realizza 12 moduli uguali
e assemblane 3
Spunti per un laboratorio di geometria, scheda 16
Tecniche per contare
Primo metodo:
9 Immaginiamo l’icosaedro in equilibrio su un vertice: ci sono 5 triangoli con il vertice nel
punto più basso del solido, 5 con il vertice nel punto più in alto e 10 a metà solido (come
negli antiprismi alternati uno all’insù e uno all’ingiù). In totale le facce sono 20.
9 Possiamo quindi vedere l’icosaedro come un antiprisma più due piramidi pentagonali, una
sopra e una sotto. Ora che abbiamo capito come sono disposti i triangoli, viene naturale
contare i vertici: uno è il vertice della piramide superiore, un altro è quello della piramide
inferiore e i due gruppi di cinque dell’antiprisma. Sono 12 in tutto.
?1 Descrivi come contare gli spigoli dell’icosaedro e del dodecaedro in gruppi di 5.
?2 Appoggiando un cubo su una faccia, descrivi il modo di contare gli spigoli in gruppi di 4.
?3 Facendo rimanere il cubo in equilibrio su un vertice, descrivi il modo di contare gli
spigoli in gruppi di 3 o 6.
Secondo metodo:
9 Sapendo che un icosaedro è composto da 20 triangoli, per contare i suoi vertici si può moltiplicare 20 per 3 (ogni
triangolo ha 3 vertici). Osserviamo che ogni vertice è condiviso da 5 triangoli, quindi dividendo 60 per 5 otteniamo 12.
?4 Con questo metodo conta gli spigoli dell’icosaedro e vertici e spigoli del dodecaedro, sapendo che quest’ultimo
ha 12 facce pentagonali.
?5 Sapendo che un ottaedro ha 8 facce triangolari e in ogni vertice se ne incontrano 4, quanti vertici e spigoli ha?
?6 Se un poliedro ha n facce, ognuna con k lati, quanti spigoli ha? Se ogni vertice è condiviso da d facce, quanti
vertici ci sono? Se un poliedro ha v vertici e ogni vertice è condiviso da d spigoli, quanti spigoli ci sono in tutto?
Terzo metodo:
9 Sapendo che ogni spigolo unisce 2 vertici, come una stretta di mano unisce 2 persone, se conosciamo il numero di
spigoli, possiamo calcolare il numero dei vertici. Ad esempio l’icosaedro ha 30 spigoli, ogni spigolo congiunge 2 vertici,
quindi ne troviamo in tutto 60. Gli spigoli si uniscono in gruppi di 5 nei vertici, quindi l’icosaedro ha 60 diviso 5 vertici.
?7 Calcola con questo metodo i vertici dei solidi regolari.
Spunti per un laboratorio di geometria, scheda 17
Teorema di Eulero I
Per ogni poliedro siano F, V, S, rispettivamente il numero di facce, vertici e spigoli. Nel 1750 il matematico svizzero Eulero
scoprì una semplice relazione tra questi tre numeri che vale per tutti i poliedri convessi: scopriamola insieme!
9 Un poliedro è convesso se il piano
Poliedro
F
V
S
di ogni faccia lascia il solido tutto
tetraedro
da una stessa parte, cioè se il
piano di ogni faccia non attraversa cubo
ottaedro
il poliedro.
dodecaedro
9 In una tabella come quella a destra inseriamo tutto ciò icosaedro
che sappiamo riguardo ai poliedri che abbiamo
prisma base triangolare
costruito fino ad ora. Aggiungi più righe se hai
prisma base quadrata
costruito altri solidi!
prisma base pentagonale
?1 Trova una formula che leghi F, V, S e
prisma base poligono di n lati
controlla che funzioni per ogni riga della
antiprisma base triangolare
tabella.
antiprisma base quadrata
9 Inventa un solido, devi essere creativo!
antiprisma base pentagonale
(Puoi aggiungere una piramide a un antiprisma o a
antiprisma base poligono di n lati
un’altra piramide…) La formula che hai trovato
piramide base triangolare
funziona? Il tuo poliedro è convesso?
piramide base quadrata
?2 Quanti vertici ci sono in un poliedro con n
piramide base pentagonale
facce triangolari? Verifica la tua risposta in
qualche esempio.
piramide base poligono di n lati
Spunti per un laboratorio di geometria, scheda 18
Teorema di Eulero II
Anche le figure piane possono essere scomposte in facce, vertici e lati. Per esempio la stellina della
figura ha15 lati, 10 vertici e 7 facce.
9 Quando studiamo queste figure, occorre fare attenzione a contare come vertici tutte le
intersezioni tra i suoi lati e come ulteriore faccia anche la porzione di piano esterna alla figura,
la cosiddetta “faccia infinita”.
?1 C’è una formula che lega il numero di facce, vertici, spigoli delle figure nel piano.
Trovala.
9 Dimostriamo tramite la Formula di Eulero che esistono esattamente 5 poliedri regolari. Il
poliedro regolare {p, q} è il solido in cui in ogni vertice s’incontrano q facce di p lati. Dalle
tecniche per contare facce, spigoli e vertici abbiamo imparato che pF = qV = 2S. Chiamiamo
questo numero k. Ad esempio per il dodecaedro e per l’icosaedro questo numero è 60.
9 Risolviamo queste relazioni per F, V, S, usando come incognite p, q e k. Otteniamo F = k / p,
V = k / q e S = k / 2. Sostituiamo nella relazione di Eulero F + V – S = 2:
Ma S = k / 2, sostituisco ed elimino la k dall’equazione, ottenendo:
Vogliamo costruire dei poliedri, quindi il numero di spigoli S e i numeri p e q devono essere positivi. Rimane da controllare
quando il denominatore è positivo, che è equivalente a chiedere
Ricorda che p e q devono essere almeno uguali a 3 (non esistono poligoni con meno di tre lati e non esistono solidi in cui in un
vertice s’incontrano meno di tre facce.)
?2 Quali sono le uniche possibilità per p e q? A quali poliedri corrispondono le coppie di numeri trovate?
?3 Abbiamo trovato una formula che dà il numero di spigoli di un solido platonico conoscendo p e q. Trova delle
formule analoghe per il numero di facce e vertici.
Spunti per un laboratorio di geometria, scheda 19
Proporzione aurea I
Per calcolare la lunghezza di un bastoncino bisogna inserire due palline alle sue estremità e misurare la distanza tra i due
centri, come in figura.
?1 Misura i bastoncini , con il righello è necessario essere il più precisi possibile.
Colore
Formato
Lunghezza
lunghezza
Blu
Giallo
Rosso
corto medio lungo corto medio lungo corto medio lungo
?2 Se hai misurato accuratamente puoi completare le seguenti relazioni:
blu corto + blu medio = _______________
giallo corto + giallo medio = _______________
rosso corto + rosso medio = _______________
?3 Ora usa una calcolatrice per eseguire le seguenti divisioni. Approssima i risultati alla seconda cifra decimale.
Se divido
Blu
Giallo
Rosso
medio : corto lungo : medio medio : corto lungo : medio medio : corto lungo : medio
Ottengo
9 Possiamo concludere che la lunghezza di un bastoncino divisa per quella del bastoncino dello stesso colore di una misura in
meno è sempre approssimativamente _________ . Abbiamo ricavato la proporzione aurea, che si indica con la lettera greca
Φ, iniziale dello scultore Fidia.
9 Anche per i bastoncini verdi troviamo lo stesso rapporto. Ci sono due diverse
famiglie di bastoncini verdi: quelli verde-blu , della stessa lunghezza di quelli blu,
che servono per realizzare gli ottagoni regolari, e quelli di colore verde sono le
diagonali di quadrati blu
Spunti per un laboratorio di geometria, scheda 20
Proporzione aurea II
9 Consideriamo i bastoncini Zome come segmenti retti, anche quelli rossi e gialli e notiamo che
possiamo creare angoli congruenti osservando bene le palline.
9 Realizza un parallelogramma usando 6 bastoncini, tutti diversi, ma solo blu e rossi.
?1 Esaminando gli angoli dimostra che è un parallelogramma.
9 Costruisci un parallelogramma con 6 bastoncini gialli e blu tutti diversi.
?2 Esaminando gli angoli dimostra che è un parallelogramma.
9 Crea un parallelogramma con 6 bastoncini gialli e rossi tutti diversi.
?3 Esaminando gli angoli dimostra che è un parallelogramma.
?4 Spiega come il tuo parallelogramma rivela le relazioni:
blu corto + blu medio = blu lungo
rosso corto + rosso medio = rosso lungo
giallo piccolo + giallo medio = giallo lungo.
9 Se pensiamo al bastoncino blu corto come all’unità, si ha che:
blu corto = 1
blu medio = Φ
blu lungo = 1 + Φ
9 Usa 4 bastoncini blu per formare un triangolo isoscele non equilatero. Sfrutta le relazioni appena trovate per costruire i
lati uguali. Unisci la pallina che non è un vertice del triangolo con l’unico vertice cui non è ancora collegata.
?5 Prova che nella figura ci sono due triangoli isosceli simili.
?6 Spiega cosa rappresenta la seguenti proporzione nei triangoli che hai costruito:
1:Φ =Φ: 1+Φ
9 Usa la relazione giallo corto + giallo medio = giallo lungo e costruisci un triangolo isoscele con base formata da due
bastoncini blu, uno corto e uno medio. Unisci le due palline che non sono vertici del triangolo.
?7 Prova che nella figura ci sono due triangoli isosceli simili.
?8 Costruisci due triangoli isosceli simili con i bastoncini blu e rossi.
Spunti per un laboratorio di geometria, scheda 21
Proporzione aurea III
Pensiamo al bastoncino blu corto come all’unità, cioè il bastoncino blu corto misura 1. Nelle schede precedenti abbiamo
trovato le relazioni tra le lunghezze dei bastoncini blu. Osserviamo che possiamo esprimere il bastoncino lungo in due
modi differenti: blu lungo = 1 + Φ oppure blu lungo = Φ2.
?1 Usa le relazioni con le somme di bastoncini per scrivere un’equazione in termini di Φ.
9 Se la risposta è corretta, abbiamo ora un’equazione di secondo grado con incognita Φ.
?3 Risolvi l’equazione. Trova la soluzione esatta e un’approssimazione numerica.
9 Se hai risolto l’equazione senza errori, hai trovato la proporzione aurea. (La radice negativa non è
interessante, perché stiamo misurando lunghezze.)
?4 Usando una calcolatrice calcola 1/ Φ e Φ 2.
9 Considera la successione 1, Φ, Φ 2, Φ 3, … Ogni termine è ottenuto dal precedente, moltiplicato per Φ.
?5 Sappiamo che 1 + Φ = Φ 2. Dimostra che Φ + Φ 2 = Φ 3 e più in generale che Φ n + Φ n+1 = Φ n+2.
9 Un rettangolo con i lati blu piccoli e medi è chiamato rettangolo aureo, perché i suoi lati sono in
proporzione Φ. Costruiscine uno e a partire da questo realizzane uno più grande, è sufficiente
aggiungere 3 bastoncini medi, come in figura.
?7 Qual è il rapporto tra i lati del nuovo rettangolo?
?8 Continua allo stesso modo e crea rettangoli aurei sempre più grandi.
9 Inscrivendo un quarto di circonferenza in ogni quadrato otteniamo la spirale aurea.
9 Un triangolo isoscele con gli angoli di 72, 72, 36 gradi è detto triangolo aureo. Costruisci un
pentagono regolare con i bastoncini blu piccoli e aggiungi un triangolo aureo a ogni lato.
9 Ora unisci i nuovi vertici, formando un pentagono regolare più grande. Il processo si può continuare.
?9 Qual è il fattore di scala tra un pentagono e l’altro?
9
La successione di Fibonacci è 1, 1, 2, 3, 5, 8, 13, … Se scriviamo F1 =1, F2 = 1, F3 = 2, otteniamo
che Fi + Fi+1 = Fi+2. Se calcoliamo il rapporto tra due termini successivi della successione, questo si
avvicina sempre più a Φ.
Spunti per un laboratorio di geometria, scheda 22
Teorema di Cartesio I
In quest’attività conosceremo il teorema scoperto dal matematico francese Cartesio. Questo teorema vale per tutti i poliedri
convessi e anche per alcuni non convessi. Vediamo di che cosa si tratta.
9 In ogni vertice di un poliedro convesso la somma degli angoli che confluiscono in esso è minore di 360 gradi (altrimenti
le facce giacciono sul piano e non otteniamo un poliedro).
9 Consideriamo ad esempio un cubo: in ogni vertice s’incontrano gli angoli retti di 3 quadrati. La somma degli angoli è 90
+ 90 + 90 = 270, e quindi minore dell’angolo giro.
9 La differenza tra l’angolo giro e la somma degli angoli di ogni vertice è detta deficit angolare.
?1 Qual è il deficit angolare
Poliedro
Numero vertici Deficit in un vertice Deficit totale
in ogni vertice di un
icosaedro regolare?
8
90
720
cubo
9 Il deficit angolare totale di un
tetraedro
poliedro è la somma dei deficit
ottaedro
angolari in ogni vertice.
dodecaedro
Calcoliamo quello del cubo. Ci
icosaedro
sono 8 vertici identici, ognuno
prisma base triangolare
con un deficit angolare di 360 –
prisma base pentagonale
270 = 90 gradi. Il deficit
angolare totale è 8 x 90 = 720
prisma base poligono di n lati
gradi.
antiprisma base pentagonale
?2 Completa una tabella
antiprisma base poligono di n lati
come quella a fianco.
?3 Possiamo formulare un’ipotesi: il deficit angolare di tutti i poliedri convessi potrebbe essere ____.
Spunti per un laboratorio di geometria, scheda 23
Teorema di Cartesio II
9 Costruisci un triangolo equilatero con il lato composto da 2 bastoncini blu corti e crea
all’interno un piccolo triangolo unendo le palline che si trovano nei punti medi dei lati.
Otteniamo un triangolo equilatero formato da 4 piccoli triangoli equilateri. Realizzane 5 e
uniscili come per formare un icosaedro.
9 Immagina di completare tutto il poliedro regolare, che sarà quindi formato da 20 x 4 = 80
piccoli triangoli equilateri. Se usiamo una struttura come questa per ricoprire una
superficie sferica otteniamo una cupola geodetica icosaedrale.
?1 Qual è il deficit angolare totale di un icosaedro in cui ogni faccia è composta da 4 piccoli triangoli? Nota che ci
sono due differenti tipi di vertici, con deficit angolari diversi. Devi fare la somma su tutti per ottenere il deficit
angolare totale.
9 Costruisci tutto o una parte di un triacontaedro rombico. Questo solido è costituito da 30
rombi. Gli angoli acuti s’incontrano in gruppi di 5 in 12 vertici, mentre gli angoli ottusi
confluiscono in gruppi di 3 in 20 vertici.
?2 Se chiamiamo x l’angolo acuto di un rombo rosso, come posso esprimere l’angolo
ottuso usando x come incognita? Qual è il deficit angolare totale di un triacontaedro
rombico?
?3 Verifica il teorema di Cartesio per una piramide con base pentagonale e superficie laterale formata da 5 triangoli
isosceli congruenti. Se gli angoli alla base di un triangolo misurano ciascuno x, quanto misura l’angolo al vertice?
Qual è il deficit angolare totale della piramide?
?4 Verifica il teorema di Cartesio per una piramide formata da un poligono regolare di n lati e da n triangoli
isosceli.
Spunti per un laboratorio di geometria, scheda 24
Teorema di Cartesio III
Anche se il teorema di Cartesio è tutto incentrato sugli angoli mentre quello di Eulero li ignora, essi sono strettamente legati.
Entrambi hanno a che fare con i solidi, cercheremo di capire per quali tipi di poliedri valgono.
9 Costruisci tutto, o una parte di dodecaedro, e inserisci una piramide pentagonale blu all’interno di
ogni faccia, come nella fotografia a lato. Abbiamo ottenuto un nuovo poliedro costituito da 60
triangoli equilateri, un esacontaedro equilatero non convesso. E’ come un dodecaedro regolare, dove
ogni faccia pentagonale è stata sostituita da una fossetta a forma di piramide.
?1 I teoremi di Eulero e di Cartesio funzionano per questo solido?
9 Realizziamo un altro solido non convesso: ha il buco come le ciambelle. Costruiamo il poliedro della
fotografia a destra: ha un buco di sezione quadrata con gli spigoli formati da bastoncini blu piccoli,
mentre le facce sono 4 rettangoli blu e 8 trapezi con i lati obliqui composti da gialli medi e le basi da
blu lunghi e corti.
?2 Il teorema di Eulero vale per questo poliedro?
?3 Il teorema di Cartesio vale per questo poliedro? Nei trapezi gli angoli sono formati da un bastoncino giallo e uno
blu. Non abbiamo ancora calcolato la loro misura, ma sappiamo che sono a due a due supplementari. Se
chiamiamo l’angolo tra la base maggiore e un lato obliquo 90-x e il suo supplementare 90 + x sarà facile calcolare
il deficit angolare totale del poliedro.
9 Prendiamo in considerazione il solido formato da due cubi che condividono un vertice.
?4 Per questo solido i due teoremi funzionano?
?5 Considera un oggetto formato da un cubo a cui togliamo un cubo più piccolo
all’interno. Rimane una regione di spazio limitata da 12 quadrati. Per questo solido
valgono i due teoremi?
9 Se le tue risposte sono giuste, hai trovato un solido per cui entrambi i teoremi funzionano, e tre per cui entrambi non
valgono.
Spunti per un laboratorio di geometria, scheda 25
Troncamento
In questa attività partiremo da un solido che conosciamo e ne costruiremo uno nuovo tramite l’operazione di
troncamento, che possiamo vedere nella figura a fianco, equivale a eliminare una porzione di solido vicino a un
vertice.
9 Un ottaedro ha 4 facce triangolari che s’incontrano in ciascun vertice.
?1 Qual è la forma del nuovo poligono che appare quando uno dei suoi vertici è troncato?
?2 In origine le facce dell’ottaedro sono tutte a forma di triangolo. Il troncamento le trasforma in un altro
poligono, quale?
9 Costruisci un ottaedro in scala tripla. Se hai i bastoncini verdi, costruisci un ottaedro regolare con gli spigoli
formati da 3 bastoncini corti, altrimenti è possibile creare un’ottima approssimazione con bastoncini rossi e
blu come in fotografia.
9 Tronca un vertice dell’ottaedro. Prima aggiungi i 4 bastoncini che uniscono le palline e poi rimuovi il
vertice con i relativi bastoncini.
9 Tronca allo stesso modo gli altri 5 vertici. Dopo aver tolto queste 6 piccole piramidi,
otteniamo l’ottaedro troncato.
?3 Descrivi il numero e il tipo di facce dopo il troncamento di tutti i solidi platonici.
?4 Se un poliedro X ha F facce e V vertici, quante facce avrà il solido ottenuto dal troncamento di X?
9 Costruiamo un cubottaedro. Partiamo da un ottaedro in scala doppia. Ora tronchiamo i suoi vertici
come prima. Di fatto stiamo troncando “un po’ di più”, cioè rimuoviamo delle porzioni maggiori di
solido, fino a ottenere che le nuove facce siano tangenti le une con le altre.
?5 Immagina di troncare in questo modo un tetraedro, che poliedro otteniamo?
9 L’ottaedro troncato e il cubottaedro sono solidi archimedei.
Spunti per un laboratorio di geometria, scheda 26
Solidi archimedei I
I solidi archimedei sono poliedri con notevoli proprietà di simmetria, le cui facce sono composte da più di un poligono. La loro
proprietà caratteristica è quella di avere tutti i vertici dello stesso tipo, cioè in ogni vertice s’incontrano lo stesso numero di
facce nello stesso ordine.
?1 Spiega perché i seguenti poliedri non sono solidi archimedei:
a. una piramide con la base quadrata e la superficie laterale composta da triangoli isosceli.
b. i solidi platonici
9 Tutti i prismi e gli antiprismi con tutte le facce regolari soddisfano le condizioni per essere solidi archimedei, ma poiché ci
sono infinite combinazioni, si preferisce metterli da parte.
9 E’ conveniente usare una notazione per ricordare quali poligoni formano le facce e in che ordine si trovano intorno ai
vertici. Per esempio l’icosidodecaedro è indicato con (3, 5, 3, 5), ciò significa che in ogni vertice di questo poliedro
s’incontrano nell’ordine un triangolo, un pentagono, un triangolo e di nuovo un pentagono.
9 In questa attività scopriremo il più regolare e interessante poliedro convesso composto solo da triangoli
equilateri e pentagoni regolari. Se serve un aiuto per costruire l’icosidodecaedro si può partire da una
pallina, inserire in tutti e 30 i buchi rettangolari bastoncini medi (o lunghi), inserire le palline alle
estremità e concludere con gli spigoli blu piccoli (o medi).
?2 Conta i triangoli e i pentagoni nell’icosidodecaedro.
?3 Secondo te perché si chiama icosidodecaedro?
?4 Trova qualche tecnica per contare vertici e spigoli.
?5 Cerca gli elementi di simmetria del poliedro.
?6 Che rapporto c’è tra la simmetria dell’icosicodecaedro e quella del dodecaedro e
dell’icosaedro?
Spunti per un laboratorio di geometria, scheda 27
Solidi archimedei II
Con il materiale Zome si possono realizzare ben 11 dei 13 solidi archimedei. Alcuni li abbiamo già incontrati, gli
altri li costruiremo insieme.
Ecco una lista dei 13 solidi archimedei:
a.
b.
c.
d.
e.
f.
g.
(3, 6, 6) tetraedro troncato
(3, 8, 8) cubo troncato
(4, 6, 6) ottaedro troncato
(5, 6, 6) icosaedro troncato
(3, 10, 10) dodecaedro troncato
(3, 4, 3, 4) cubottaedro
(3, 5, 3, 5) icosidodecaedro
h. (3, 4, 4, 4) rombicubottaedro
i. (3, 4, 5, 4) rombicosidodecaedro
j. (4, 6, 8) cubottaedro troncato
k. (4, 6, 10) icosidodecaedro troncato
l. (3, 3, 3, 3, 4) cubo camuso
m. (3, 3, 3, 3, 5) dodecaedro camuso
Qualche suggerimento per la costruzione:
a. (3, 6, 6) tetraedro troncato Se non riesci a costruire intorno a un vertice un triangolo equilatero, e poi
due esagoni regolari, inizia da un tetraedro in scala tripla, cioè con i lati composti da 3 bastoncini
verdi corti, e poi tronchi i 4 vertici.
b. (3, 8, 8) cubo troncato Troncando un cubo in cui ogni spigolo è formato da
tetraedro troncato
3 bastoncini blu corti, si ottengono ottagoni irregolari, che possiamo
sostituire con ottagoni regolari usando i bastoncini di colore verde-blu.
Altrimenti possiamo realizzare 6 ottagoni e riunirli come i quadrati di un cubo. Inizia con due
ottagoni che condividono un bastoncino blu, e i cui piani sono perpendicolari.
cubo troncato
Spunti per un laboratorio di geometria, scheda 28
Solidi archimedei III
c. (4, 6, 6) ottaedro troncato Troncare un ottaedro costruito in tripla scala con i bastoncini
verdi, oppure una sua approssimazione con i bastoncini blu e rossi.
d. (5, 6, 6) icosaedro troncato Realizza un icosaedro con tutti
gli spigoli costituiti da 3 bastoncini blu corti e tronca i
vertici. Il risultato è simile a un pallone da calcio, come puoi
vedere nella fotografia a sinistra.
ottaedro troncato
e. (3, 10, 10) dodecaedro troncato Costruisci un dodecaedro
con gli spigoli formati da 3 bastoncini blu: due corti e uno di
lunghezza media nel centro. Con quest’accortezza dopo il
troncamento otteniamo decagoni regolari, vedi fotografia a
destra.
icosaedro troncato
cubottaedro
f. (3, 4, 3, 4) cubottaedro Costruisci un cubo o un ottaedro
regolare in scala doppia, e tronca fino al punto medio degli
spigoli. Se non possiedi i bastoncini verdi, realizza
quest’approssimazione: al posto dei quadrati del cubottaedro
crea un rettangolo composto da due bastoncini rossi corti e
due blu piccoli. Costruisci l’ottaedro in scala 2 e poi tronca i
6 vertici.
dodecaedro troncato
g. (3, 5, 3, 5) icosidodecaedro Tronca fino al punto medio
degli spigoli un icosaedro o un dodecaedro realizzato in
scala doppia, oppure parti da una pallina e inserisci un
bastoncino blu in ogni suo buco a forma rettangolare.
Spunti per un laboratorio di geometria, scheda 29
icosidodecaedro
Solidi archimedei IV
h. (3, 4, 4, 4) rombicubottaedro Inizia con un ottagono regolare costruito con 4 bastoncini blu
e 4 verde-blu. Usa quest’ottagono per realizzare un prisma retto con tutte le facce laterali
quadrate. Ora con attenzione devi costruire intorno a ogni vertice un triangolo equilatero e
3 quadrati. Alla fine ti accorgerai che ci sono due prismi ottagonali
perpendicolari fra loro.
i. (3, 4, 5, 4) rombicosidodecaedro Realizza una versione in grande di una
pallina, ma con quadrati anziché rettangoli, disposti come in fotografia.
rombicubottaedro
cubottaedro troncato
j. (4, 6, 8) cubottaedro troncato Costruisci 6 ottagoni regolari con i
rombicosidodecaedro
bastoncini blu e quelli verde-blu. Con un ottagono adagiato sul
tavolo, prendine un secondo e mettilo verticalmente vicino al primo in modo da avere
due spigoli blu vicini e paralleli. Se necessario ruotane uno di 90 gradi affinché le
palline siano parallele. Usando due bastoncini verde-blu unisci i bastoncini blu paralleli
per formare un quadrato a 45 gradi rispetto agli ottagoni. Allo stesso modo unisci altri 3
ottagoni al primo, e termina costruendo tutti i quadrati.
k. (4, 6, 10) icosidodecaedro troncato Inizia con un decagono
regolare e costruisci un quadrato all’esterno di 5 spigoli, uno sì
e uno no. Nei rimanenti 5 spigoli concludi gli esagoni.
Continua con le stesse forme fino a chiudere il poliedro,
controllando di avere in ogni vertice un quadrato, un esagono e
un decagono.
Il cubo camuso e il dodecaedro camuso non possono essere realizzati con il materiale Zome.
Spunti per un laboratorio di geometria, scheda 30
icosidodecaedro
troncato
Solidi archimedei V
?1 Riassumiamo tutto ciò che abbiamo imparato sui solidi archimedei in una tabella dove inseriremo il numero di facce,
vertici e spigoli, gli elementi di simmetria e il nome del solido platonico che ha la stessa simmetria.
Nome
Assi di
Assi di
Assi di
Assi di
Piani di Simmetria
F V S
ordine 5 ordine 4 ordine 3 ordine 2 simmetria
del
poliedro
8 18 12
0
0
4
3
6
tetraedro
tetraedro troncato
cubo troncato
ottaedro troncato
icosaedro troncato
dodecaedro troncato
cubottaedro
icosidodecaedro
rombicubottaedro
rombicosidodecaedro
cubottaedro troncato
icosidodecaedro troncato
cubo camuso
dodecaedro camuso
Spunti per un laboratorio di geometria, scheda 31
Zonoedri I
Ogni poliedro composto interamente da parallelogrammi è un tipo do zonoedro.
9 Il termine romboedro può essere usato per riferirsi a un poliedro costituito da rombi, ma convenzionalmente si usa solo per
gli esaedri (cioè i poliedri con 6 facce), in cui le facce sono rombi tutti uguali. Il cubo risulta essere un caso particolare di
romboedro.
?1 Con i bastoncini rossi si può creare una sola forma di rombo, trovala e usala per costruire due
tipi di romboedro, ognuno con 12 spigoli rossi. Studia le differenze tra i due solidi.
9 Entrambi i modelli che hai realizzato sono prismi non retti a base rombica. Vengono chiamati
romboedro acuto e romboedro ottuso a seconda del tipo di angolo che incontra l’asse di simmetria di
ordine 3.
?2 Costruisci le due forme di rombo giallo. Usa quello più largo per creare due tipi diversi di romboedro.
9 Un esaedro rombico ha 6 facce a forma di rombo, ma non è necessario siano tutte congruenti. Gli spigoli devono essere tutti
uguali, ma non gli angoli. Il romboedro è un caso particolare di esaedro rombico in cui tutte le facce sono identiche.
?3 Realizza con i bastoncini blu o gialli un esaedro rombico che non sia un romboedro.
?4 Perché con i bastoncini rossi non si può realizzare un esaedro rombico che non sia un romboedro?
9 Osserva che ogni romboedro ha un asse di simmetria di ordine tre. Questo ci suggerisce un
altro metodo per costruirli. Partiamo da un bastoncino giallo corto inserito in una pallina. Non
sarà parte del solido finale, ma ci ricorderà la simmetria che dobbiamo seguire. Inserisci 3
bastoncini nella pallina, di qualsiasi colore, ma tutti della stessa misura. Aggiungere le palline
e i bastoncini paralleli necessari per terminare i tre rombi. Concludere con i tre rombi che
s’incontrano nel vertice opposto a quello originale. Questo metodo può essere generalizzato
per creare poliedri rombici con assi di simmetria di ordine n.
9 Costruiamo uno zonoedro con un asse di simmetria di ordine 5: partiamo con un bastoncino
rosso in una pallina e ricordiamo che tutte le facce devono essere rombi. Realizza la stella
come in figura e unisci uno dopo l’altro gli spigoli paralleli a quelli che hai già. Ottieni
l’icosaedro rombico.
?5 Quante facce ha il solido che hai costruito? Da quanti tipi diversi di rombo è composto?
Spunti per un laboratorio di geometria, scheda 32
Zonoedri II
Ci sono esattamente 4 poliedri con più di sei facce composti esclusivamente da rombi:
1.
2.
3.
4.
l’icosaedro rombico conposto di 20 rombi rossi
il dodecaedro rombico composto di 12 rombi gialli
il dodecaedro rombico del secondo tipo conposto di 12 rombi rossi
il triacontaedro rombico composto di 30 rombi rossi
9 Costruiamo il dodecaedro rombico. Si parte da un
cubo di bastoncini blu, si applica una piramide gialla
su ogni faccia, e infine si rimuovono gli spigoli del
cubo. Nel dodecaedro rombico si nota molto bene la
dualità tra cubo e ottaedro: le palline verdi sono i
vertici del cubo, quelle
viola sono i vertici
dell’ottaedro.
9 Il dodecaedro rombico del secondo tipo è rappresentato nella figura a lato: è chiamato in questo
modo per distinguerlo dal dodecaedro rombico giallo, che è molto più simmetrico.
9 Realizziamo il triacontaedro rombico in uno dei due modi già visti
prima: costruisci un icosaedro con il lato blu lungo o medio e innalza su
ogni faccia una piccola piramide a base triangolare, oppure costruisci un dodecaedro e innalza una
piccola piramide pentagonale su ogni faccia. Infine rimuovendo tutti i bastoncini blu si ottiene il
poliedro della fotografia a sinistra.
9 Tutti i poliedri di quest’attività sono zonoedri. Uno zonoedro è un poliedro convesso in cui ogni
faccia ha un numero pari di lati, e i lati opposti sono paralleli.
Spunti per un laboratorio di geometria, scheda 33
Zonoedri III
9 Prendi il dodecaedro rombico del secondo tipo e scegli un suo spigolo. Osserva che si possono trovare altri 5 spigoli
paralleli a quello che hai scelto. L’insieme degli spigoli paralleli è chiamata zona di spigoli, la cintura di facce che li
condividono è detta zona di facce.
?1 Conta le zone del dodecaedro rombico del secondo tipo.
9 Il numero delle zone è lo stesso delle direzioni degli spigoli del poliedro. Scegli due zone e
nota che si incontrano due volte, condividendo due facce opposte e parallele. In generale, se
ci sono n zone, ogni zona incontra due volte le altre n-1 zone.
?2 Completa la tabella:
Zonoedro
romboedro
Numero di zone Numero di facce
3
6
dodecaedro rombico
icosaedro rombico
?3
triacontaedro rombico
?3 Trova una formula per calcolare il numero di facce conoscendo il numero di zone.
?4 Se togli una zona di 6 spigoli paralleli da un dodecaedro rombico e poi riunisci le due
parti di solido che rimangono, che poliedro ottieni?
?5 Prendi il triacontaedro e elimina una zona. Riunendo le due parti rimanenti quale solido ottieni?
?6 Rimuovendo una zona dall’icosaedro rombico cosa succede?
Spunti per un laboratorio di geometria, scheda 34
Zonoedri IV
9 Un ipercubo è l’analogo del cubo in n dimensioni. Appoggia sul tavolo una pallina, poi un bastoncino blu corto con due
palline alle estremità, un quadrato formato da blu corti, e poi un cubo. Questi sono rispettivamente gli ipercubi di
dimensione 0, 1, 2, 3.
9 Non si può costruire un ipercubo di dimensione 4, perché viviamo in un modo tridimensionale; possiamo però realizzare
vari modelli di proiezioni di un ipercubo in dimensione 3. E’ una situazione analoga a disegnare su foglio di carta un
cubo di dimensione 3. Nella figura sono proposti tre modi di proiettare un cubo in 2 dimensioni.
9 Costruiremo analoghi modelli per le proiezioni di un ipercubo di dimensione 4.
Primo modello: costruisci un cubo grande con gli spigoli blu lunghi e uno piccolo con gli spigoli blu
corti, infine collegali usando otto bastoncini gialli. Si ottiene una figura simile immergendo un cubo in
abbondante acqua saponata: guarda la bolla al centro del cubo nella figura a lato.
?1 In che senso questo modello è analogo al primo modo di proiettare un cubo su un foglio di carta?
Secondo modello: crea un dodecaedro rombico con gli spigoli formati da bastoncini gialli lunghi. Metti una pallina nel suo
centro e uniscila con 4 bastoncini gialli lunghi a 4 vertici, disposti come quelli di un tetraedro regolare. Rimangono 4 vertici
liberi, uniscili a una seconda pallina posta nel centro del poliedro. Non aver paura di rompere i bastoncini, sono piuttosto
flessibili.
?2 Spiega in che modo questo poliedro rappresenta una proiezione simile al secondo modo di disegnare un cubo.
Terzo modello: Crea due cubi della stessa dimensione che si collegano con 8 segmenti paralleli.
?3 Spiega in che modo questo poliedro rappresenta una proiezione simile al terzo modo di disegnare un cubo.
Spunti per un laboratorio di geometria, scheda 35