Y557 - ESAME DI STATO DI LICEO SCIENTIFICO

Y557 - ESAME DI STATO DI LICEO SCIENTIFICO -2006
CORSO SPERIMENTALE
PIANO NAZIONALE INFORMATICA
Tema di: MATEMATICA
QUESTIONARIO
1. Si narra che l’inventore del gioco degli scacchi chiedesse di essere compensato con chicchi di
grano: un chicco sulla prima casella, due sulla seconda, quattro sulla terza e così via, sempre
raddoppiando il numero dei chicchi, fino alla 64a casella. Assumendo che 1000 chicchi pesino
circa 38g, calcola il peso in tonnellate della quantità di grano pretesa dall’inventore.
Casella
Chicchi
1
1
2
2*1=21
3
2*2=22=4
4
2*4=23=8
…
…
n
2*2n-2=2n-1
64
263
Sommando i chicchi Somma  1  2  22  ...  263
xn 1
Dato che 1  x  x 2  ...  x n 1 
ho che
x 1
264  1
2
63
Somma  1  2  2  ...  2 
 1,84 1019
2 1
Peso Peso 
1,84 1019
9, 22 1018
38 g 
38Kg  7 1014 Kg
6
1000
10
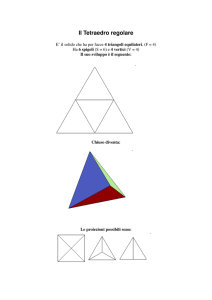
2. I poliedri regolari – noti anche come solidi platonici – sono, a meno di similitudini, solo
cinque: il tetraedro, il cubo, l’ottaedro, il dodecaedro e l’icosaedro. Sai dimostrarlo?
In ogni vertice deve avere almeno 3 facce. E complessivamente la somma deve essere <360.
1) se il poligono regolare è un triangolo equilatero.
N facce= 3 angolo 60° da cui 60*3=180 (tetraedro)
N facce=4 angolo 60° da cui 60*4=240 (ottaedro)
N facce=5 angolo 60° da cui 60*5=300 (icosaedro)
N facce=6 angolo 60° da cui 60*6=360 non esiste
2) se il poligono regolare è un quadrato.
N facce= 3 angolo 90° da cui 90*3=270 (cubo)
N facce=4 angolo 90° da cui 90*4=360 non esiste
3) se il poligono regolare è un Pentagono.
N facce= 3 angolo 108° da cui 108*3=324 (dodecaedro)
N facce=4 angolo 108° da cui 108*4=432 non esiste
4) se il poligono regolare è un Esagono.
N facce= 3 angolo 120° da cui 120*3=360 non esiste
4. Si dimostri che l’equazione sen x = x −1 ha una e una sola radice α e, utilizzando una
calcolatrice tascabile, se ne dia una stima. Si descriva altresì una procedura di calcolo che
consenta di approssimare α con la precisione voluta.
Considerando al funzione
f ( x)  sin x  x  1
f '( x)  cos x  1  0 cos x  1 Mai positiva
Da cui funzione sempre decrescente.
Dato che

f '( x)  0 per x=0°

f ( )  sin x  x  1  2   0
2
2
f ( )  sin x  x  1  1 

2
0
 
Nell’intervallo  ;   ha una sola soluzione. Per il teorema degli zeri di una funzione continua.
2 
Per calcolare lo zero approssimato uso il metodo di Newton.
f ( x)  sin x  x  1
f '( x)  cos x  1
f ( xn )
f ( x0 )
xn 1  xn 
x1  x0 
f '( xn )
f '( x0 )
errore E | xn   |
x
1
2,830488
2,049555
1,938656
1,934569
f ( xn )
f ( xn )

 10t , t>0
f '( xn ) max f '( x)
f
f'
Passo
Errore
0,841471 -0,4597
0
-1,52438
-1,952
1 0,780932
-0,16199 -1,46068
2 0,110899
-0,00556 -1,35962
3 0,004087
-7,8E-06 -1,3558
4 5,75E-06
6. L’equazione risolvente un dato problema è: k cos2x − 5k + 2 = 0 dove k è un parametro reale e
x ha le seguenti limitazioni: 15° < x < 45° . Si discuta per quali valori di k le radici
dell’equazione siano soluzioni del problema.
7. Bruno de Finetti (1906-1985), tra i più illustri matematici italiani del secolo scorso, del quale
ricorre quest’anno il centenario della nascita, alla domanda: “che cos’è la probabilità?” era
solito rispondere: “la probabilità non esiste!”. Quale significato puoi attribuire a tale risposta?
E’ possibile collegarla ad una delle diverse definizioni di probabilità che sono state
storicamente proposte?
8. Un tiratore spara ripetutamente ad un bersaglio; la probabilità di colpirlo è di 0,3 per ciascun
tiro. Quanti tiri deve fare per avere probabilità ≥ 0,99 di colpirlo almeno una volta?
Se p=0,3 e se q=0,7 è la probabilità contraria
n
applicando la distribuzione binomiale nel ho che Pk  P( X  k )    p k q n k
k 
n
Se su n tiri P0    p 0 q n  q n  (0, 7)n
E’ la probabilità di no colpirlo mai
0
La probabilità di colpirlo almeno una volta P  P( X  1)  1  (0,7)n  0,99
Da cui 1  (0, 7)n  0,99 (0, 7)n  0, 01 (Dato ln0,7<0 la disequazione cambia verso di nuovo)
ln 0, 01
n
 12,9 Quindi occorre fare almeno 13 tiri. .
ln 0, 7
9. Della funzione f (x) si sa che è derivabile e diversa da zero in ogni punto del suo dominio e,
ancora, che: f ′(x)= f (x) e f (0)= 1. Puoi determinare f (x)?
L’unica funzione che derivata mi da se stessa è f ( x)  e x
oppure
f '( x)
f '( x)
f '( x)  f ( x)
 1integrando ambo i membri ho che 
dx   dx
f ( x)
f ( x)
 f ( x)  e x  k  f ( x)  e x  k
 f ( x)  e x  k
df ( x)
ln
f
(
x
)

x

k
e

dx
 k


 f ( x) 
e  1
 f (0)  1
k  0
x
f ( x)  e
10. Tenuto conto che:
1
dx
 1 x
0
2


4
calcola un’approssimazione di π utilizzando uno dei metodi di
integrazione numerica studiati.
Utilizzo il metodo dei rettangoli. Calcolo
s   f ( x)dx  x  f ( x0 )  f ( x1 )  ...  f ( xn1 )  E
b
a
b
S   f ( x)dx  x  f ( x1 )  f ( x2 )  ...  f ( xn ) 
a
Se x 
ba
n
Con x0  a x1  a 
E quindi I 
sS
2
Se n=4 ho
ba 1
1

x0  0 x1 
n
4
4
1 1
2
3 
s   f ( )  f ( )  f ( )
4 4
4
4 
x
f(x)
0
1
0,25 0,941176
0,5
0,8
0,75
0,64
1
0,5
s=
S=
I=
0,845294
0,720294
0,782794
pi greco=
I*4=
ba
n
x2  2
x2  a  2
1
4
ba
n
x3  3
xn  b
1
x4  1
4
1 2
3

S   f ( )  f ( )  f (1) 
4 4
4

a=
b=
n=
delta x
0
1
4
0,25
3,131176
Ovviamente con maggiori divisione ottengo un risultato migliore.