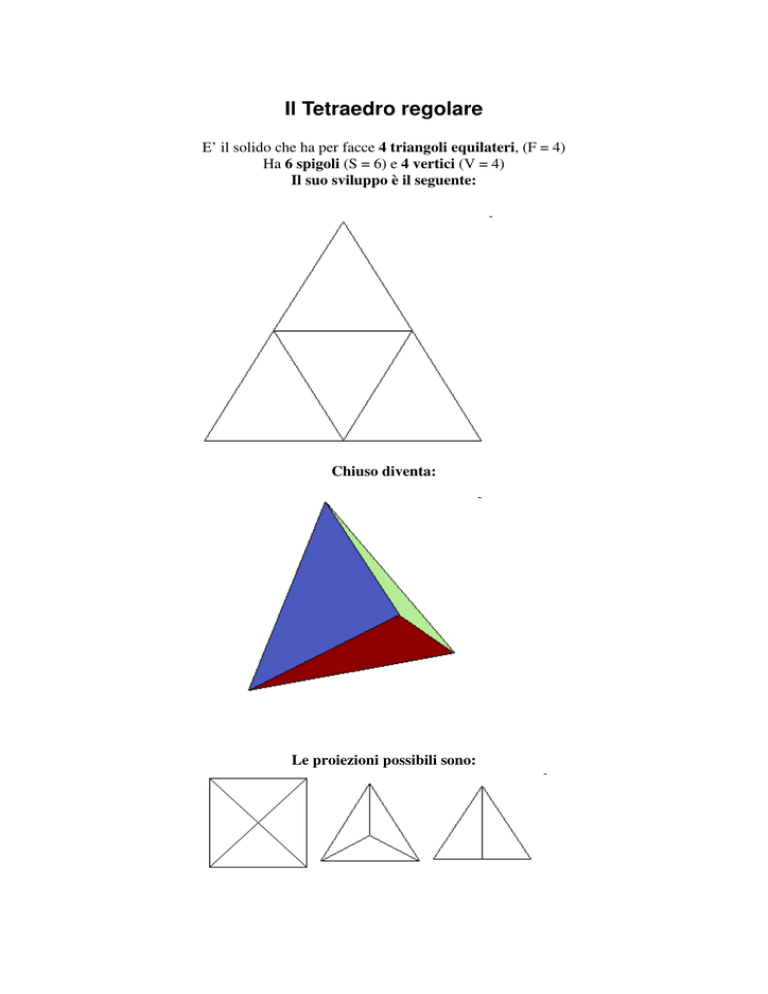
Il Tetraedro regolare
E’ il solido che ha per facce 4 triangoli equilateri, (F = 4)
Ha 6 spigoli (S = 6) e 4 vertici (V = 4)
Il suo sviluppo è il seguente:
Chiuso diventa:
Le proiezioni possibili sono:
I suoi assi di simmetria sono:
Può essere pensato inscritto ad un cubo:
E’ il duale di se stesso:
Dato lo spigolo l per calcolare il raggio della sfera inscritta, il raggio della sfera circoscritta, il
volume e l’area della sua superficie totale si procede come segue:
D
Se il lato del TETRAEDRO è l
DK = KC =
O
A
HK =
l
3
6
HB =
l
3
3
l
3
2
C
H
K
B
2
l
l
DH = l −
3 =
6
3
3
2
Indicato con R Il raggio della sfera circoscritta ( DO = OB ) e con r il raggio della sfera inscritta
applicando il teorema di Pitagora al triangolo OHB si ottiene:
R=
l
l
6 e OH = r =
6
4
12
·
.
Per calcolare l’angolo tra le facce, basta calcolare l’angolo α ° = DKC
Si tratta di risolvere il triangolo KCD del quale si conoscono i tre lati.
3
1
Si ottiene : α ° = 2 ArcSin
; 70°31' 43'', 6
= 2 ArcSin
3
2 Sin60°
Volume e area totale sono immediati:
AT = l 2 ⋅ 3
V=
l3
⋅ 2
12
Esaedro Regolare o Cubo
E’ il solido che ha per facce 6 quadrati (F = 6)
Ha 12 spigoli (S = 12) e 8 vertici (V = 8)
Il suo sviluppo è il seguente:
Chiuso diventa:
Le proiezioni possibili sono:
I suoi assi di simmetria sono:
Il cubo e il Dodecaedro:
Il cubo e l’Icosaedro:
Come ricoprire il cubo:
Il cubo e l’esagono:
Trasformato per inversione:
Esaedro regolare o Cubo di spigolo l.
L’angolo diedro tra le facce è 90°
l
Il raggio della sfera inscritta è
2
Il raggio della sfera circoscritta è
AT = 6 ⋅ l 2
V = l3
l
3
2
Ottaedro Regolare
E’ il solido che ha per facce 8 triangoli equilateri, (F = 8)
Ha 12 spigoli (S = 12) e 6 vertici (V = 6)
Il suo sviluppo è il seguente:
Chiuso diventa:
Le sue proiezioni sono:
I suoi assi di simmetria sono:
L’Ottaedro e l’Esagono
Il suo Duale è il Cubo
Ottaedro regolare di lato AB = l
l
2
l
CH =
3
2
l
CO =
2
2
·
α = OHC
OH =
Il raggio della sfera circoscritta corrisponde a CO.
IL raggio della sfera inscritta corrisponde all’altezza
del triangolo rettangolo COH relativa alla base CH.
Pertanto:
l
2
2
l
r=
6
6
R=
Poiché Sinα =
6
3
l'angolo tra le facce è
2α = 2 ArcSin
6
; 109°28'16 '', 39
3
Ora è facile calcolare l’area della superficie totale e il volume:
AT = 2 ⋅ l 2 ⋅ 3
V=
l3
⋅ 2
3
Il Dodecaedro Regolare
E’ il solido che ha per facce 12 pentagoni regolari, (F = 12)
Ha 30 spigoli (S = 30) e 20 vertici (V = 20)
Il suo sviluppo è il seguente:
Chiuso diventa:
Le proiezioni possibili sono:
I suoi assi di simmetria sono:
Può essere pensato inscritto ad un cubo:
I rettangoli aurei e il Dodecaedro:
Il duale del Dodecaedro è l’Icosaedro
Il Dodecaedro regolare è formato da 12 facce
pentagonali, congiungendo 3 vertici come in figura si
ottiene una piramide che ha come base un triangolo
equilatero. Consideriamo due punti su due lati contigui
della base A e B e da questi tracciamo due segmenti uguali
e perpendicolari AC e BC al lato che va al vertice della
piramide come nella seguente figura:
L’angolo ACD è retto per costruzione,
L’angolo ADC misura 36°
L’angolo ADE misura 30°
Perciò
AC = ADSin36°
AE = ADSin30°
ACB AE Sin30°
=
=
2
AC Sin36°
·ACB = 2 ArcSin Sin30°
Sin36°
Sin
che l’angolo diedro tra le facce.
Ora, consideriamo la piramide che ha per base una faccia del dodecaedro e per altezza il raggio
della sfera inscritta.
Poiché l’angolo interno di un pentagono regolare
misura 108°, l’angolo OBA = 54°.
l
AB =
2
l
OA = Tan54°
2
Quindi l’area di base sarà
l
l l 5
5 ⋅ OA ⋅ = 5 ⋅ Tan54° ⋅ ⋅ = ⋅ Tan54° ⋅ l 2
2
2 2 4
Sin30°
OD = OA ⋅ Tan ArcSin
=
Sin36°
1
Sin30°
Tan54° ⋅ Tan ArcSin
⋅l
2
Sin36°
che è il raggio della sfera inscritta e DB è il raggio della sfera circoscritta.
Volume e area totale sono immediati.
Icosaedro Regolare
E’ il solido che ha per facce 20 triangoli equilateri, (F = 20)
Ha 30 spigoli (S = 30) e 12 vertici (V = 12)
Il suo sviluppo è il seguente:
Chiuso diventa:
Le sue proiezioni sono:
I suoi assi di simmetria sono:
Il suo duale è il dodecaedro regolare:
L’Icosaedro Regolare è formato da 20 facce di lato l.
Si consideri la piramide che ha per base un pentagono
regolare e per facce 5 triangoli equilateri come in figura.
Si prendano su due lati consecutivi i punti A e C in modo
che AB = BC, si traccino i segmenti AD e CD in modo che
gli angoli ADB e CDB siano retti.
Si sa che l’angolo ABD = 60° e che l’angolo ABE = 54°,
pertanto:
AD = AB ⋅ Sin60°
AE = AB ⋅ Sin54°
da ciò si ricava
AE Sin54°
=
AD Sin60°
Sin54°
·
ADC = 2 ⋅ ArcSin
; 138°11' 22 '',86
Sin60°
Abbiamo così calcolato l’angolo tra due facce dell’icosaedro regolare.
Sin ·
ADE =
Un piano che passa per il centro O dell’icosaedro e taglia a metà gli spigoli genera un decagono di
centro O con lati pari a l/2.
In prospettiva si ha la seguente figura:
l
2
l
OE = Cotg18°
2
l
EP =
3
12
EA =
OP è il raggio della sfera inscritta: r. Perciò, con Pitagora si ricava
r = OE 2 − EP 2 =
l2
l2
Cotg 218° −
ecc.
4
48












