Verifica di Elettronica

Istituto Scolastico Superiore Statale “G. B. Rubini” di Romano di Lombardia
Verifica di Elettronica
www.marcochirizzi.it
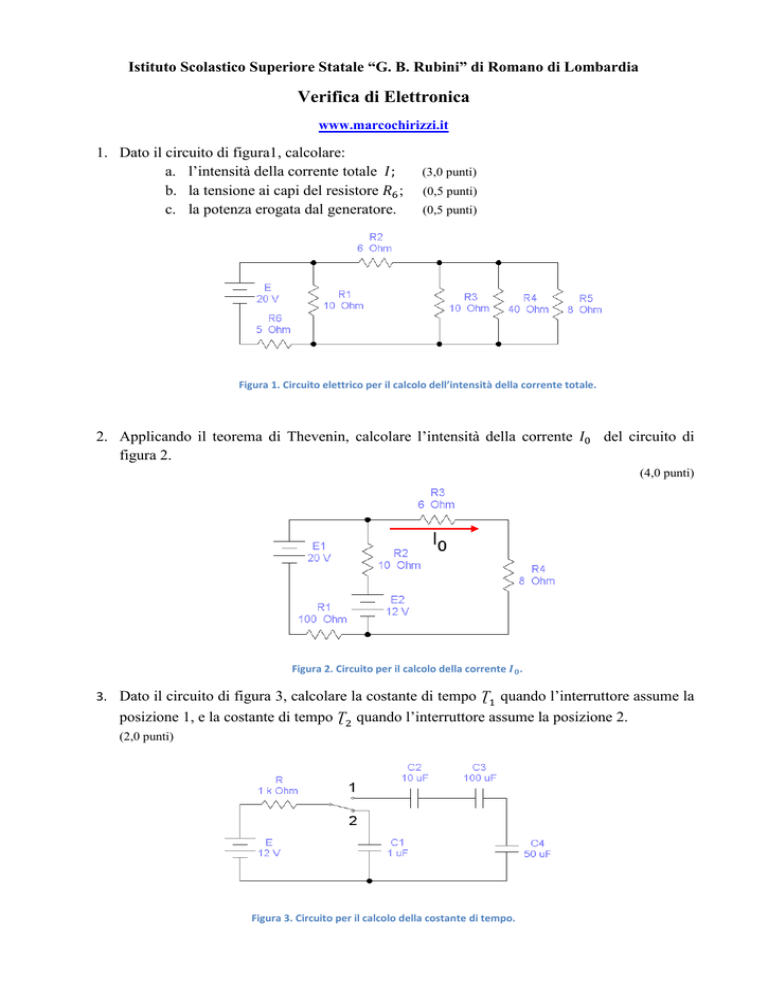
1. Dato il circuito di figura1, calcolare:
a. l’intensità della corrente totale
b. la tensione ai capi del resistore ;
c. la potenza erogata dal generatore.
(3,0 punti)
(0,5 punti)
(0,5 punti)
Figura 1. Circuito elettrico per il calcolo dell’intensità della corrente totale.
2. Applicando il teorema di Thevenin, calcolare l’intensità della corrente
figura 2.
del circuito di
(4,0 punti)
Figura 2. Circuito per il calcolo della corrente
quando l’interruttore assume la
quando l’interruttore assume la posizione 2.
3. Dato il circuito di figura 3, calcolare la costante di tempo
posizione 1, e la costante di tempo
.
(2,0 punti)
Figura 3. Circuito per il calcolo della costante di tempo.
SOLUZIONE DEL PRIMO ESERCIZIO
L’intensità della corrente totale si calcola come segue:
La resistenza totale
si calcola semplificando il circuito:
le resistenze
ed
risultano collegate in parallelo fra di loro, per tanto possono essere
sostituite con una sola resistenza di valore
dato da:
Le resistenze
sono percorse dalla stessa corrente, quindi risultano in serie e possono
essere sostituite da una resistenza di valore
dato da:
Quest’ultima resistenza è collegata in parallelo ad
, quindi si ha:
A questo punto, il circuito di partenza si riduce ad una sola maglia, composta dal generatore e da
due resistenze in serie,
. La resistenza totale del circuito risulta:
Dalla prima legge di Ohm, si ha:
La tensione ai capi del resistore
si calcola come segue:
mentre la potenza erogata dal generatore è data da:
SOLUZIONE DEL SECONDO ESERCIZIO
Il ramo interessato alla corrente
è quello composto dalle resistenze
, pertanto conviene staccare proprio questo ramo. Il circuito per il calcolo della tensione
equivalente di Thevenin e della resistenza equivalente di Thevenin è riportato in figura 2a.
Figura 2a. Circuito privato del ramo composto da
.
Per il calcolo della resistenza equivalente di Thevenin, bisogna fare riferimento al circuito riportato
in figura 2b, ottenuto cortocircuitando tutti i generatori di tensione.
Figura 2b. Circuito per il calcolo della resistenza equivalente di Thevenin.
Come si può notare, le resistenze
e B. Essendo per definizione
sono collegate in parallelo fra di loro rispetto ai punti A
, possiamo scrivere:
Per il calcolo della tensione equivalente di Thevenin, che per definizione risulta
,
bisogna invece fare riferimento al circuito di figura 2a. Se si ricorre al secondo principio di
Kirchhoff, si sceglie il verso di percorrenza della corrente, per esempio quello orario, ed il verso di
percorrenza della maglia ( vedi figura 2c ).
Figura 2c. Scelta del verso di percorrenza della corrente e della maglia.
Una volta stabilite le polarità della tensione ai capi di , si procede con la scrittura dell’espressione
di
, tenendo conto che si parte dal punto A e si termina il percorso in B. In formula si ha:
dove:
quindi:
Si può arrivare allo stesso risultato applicando il principio di Millmann (vedi figura 2d):
denotando con
le correnti di corto circuito, la tensione
si calcola come segue:
Figura 2d. Applicazione del principio di Millmann.
Il circuito equivalente di Thevenin è riportato in figura 2e.
Figura 2e. Circuito equivalente di Thevenin
Applicando la legge di Ohm, l’intensità della corrente
si calcola come segue:
SOLUZIONE DEL TERZO ESERCIZIO
Quando l’interruttore assume la posizione 1, la costante di tempo del circuito vale:
Quando l’interruttore assume la posizione 2, la costante di tempo del circuito risulta: