Calcolo della derivata mediante la definizione

1
www.matematicagenerale.it
Calcolo delle derivate applicando la definizione di alcune funzioni.
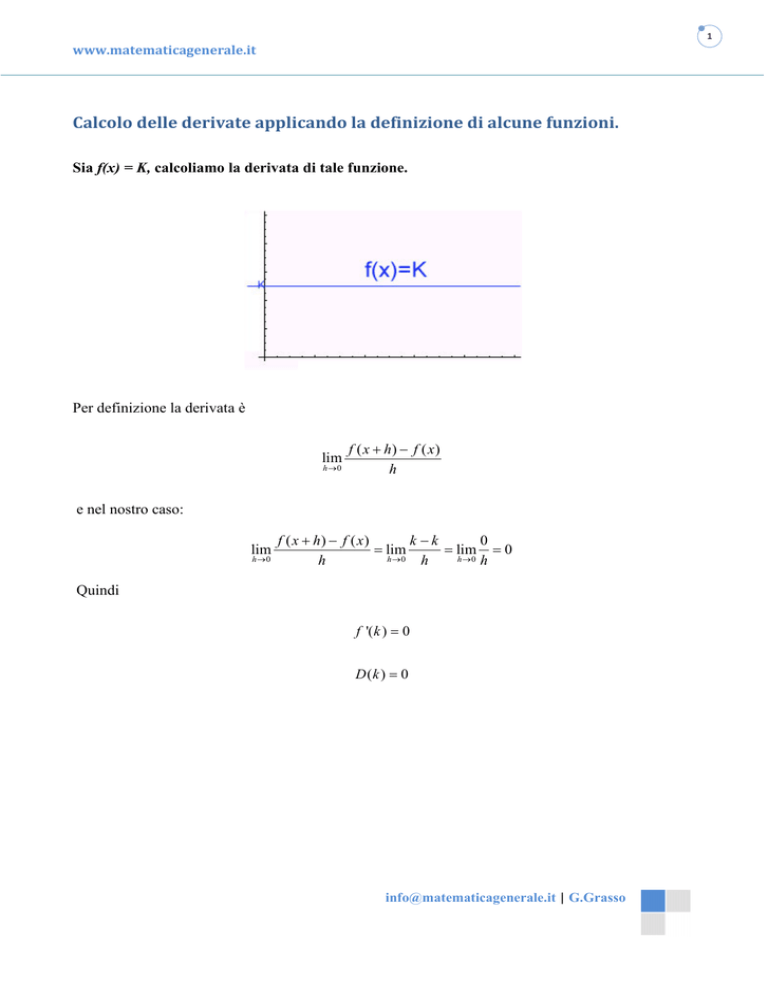
Sia f(x) = K, calcoliamo la derivata di tale funzione.
Per definizione la derivata è
lim
h0
f ( x  h)  f ( x )
h
e nel nostro caso:
lim
h0
f ( x  h)  f ( x )
k k
0
 lim
 lim  0
h0
h0 h
h
h
Quindi
f '( k )  0
D (k )  0
[email protected] | G.Grasso
2
www.matematicagenerale.it
Calcoliamo la derivata della funzione f(x) = x.
Applichiamo la definizione di derivata:
lim
h0
f ( x  h)  f ( x )
h
Ovvero nel nostro caso:
lim
h0
f ( x  h)  f ( x )
( x  h)  x
h
 lim
 lim  1
h

0
h

0
h
h
h
D( x)  1
Calcoliamo la derivata della funzione f(x)=x2
Applichiamo la definizione di derivata:
lim
h0
f ( x  h)  f ( x )
h
Ovvero nel nostro caso:
lim
h 0
f ( x  h)  f ( x )
( x  h) 2  x 2
x 2  2 xh  h 2  x 2
h(2 x  h)
 lim
 lim
 lim
 2x
h 0
h 0
h 0
h
h
h
h
D( x 2 )  2 x
[email protected] | G.Grasso
3
www.matematicagenerale.it
La derivata della funzione f(x )= xn ( n )
Applicando la definizione di si può calcolare la derivata della funzione f(x) =xn
f '( x)   x n 1
D( x n )   x n1
Applichiamo la definizione di derivata
lim
h0
f ( x  h)  f ( x )
h
tenendo conto che:
si ha:
Di seguito proveremo questa regola con il principio di induzione.
Calcoliamo, usufruendo della definizione, la derivata di f(x)=lnx
Applichiamo la definizione di derivata:
lim
h0
f ( x  h)  f ( x )
h
Nel nostro caso f(x+h)= ln (x+h) e f(x) = lnx pertanto:
lim
h0
f ( x  h)  f ( x )
ln( x  h)  ln( x )
ln( x  h)
ln x
 lim
 lim
 lim
h0
h0
h0 h
h
h
h
Mettiamo in evidenza x :
[email protected] | G.Grasso
4
www.matematicagenerale.it
h 

ln  x(1  ) 
ln x
x 
lim 
 lim

h 0
h 0 h
h
Applichiamo la proprietà del prodotto di logaritmi:
h
h
ln(1  )  ln x
ln(1  )
ln x
x
x  lim ln x  lim ln x 
lim
 lim
 lim
h 0
h

0
h

0
h 0 h
h 0 h
h
h
h
Semplifichiamo i termini simili e riconosciamo il limite fondamentale nel primo limite:
lim
x 0
ln(1  x )
1
x
quindi dividiamo e moltiplichiamo per x al denominatore:
h
ln(1  )
x 1
 lim
h 0
h
x
x
x
Dunque:
D (ln x ) 
1
x
[email protected] | G.Grasso
5
www.matematicagenerale.it
Calcoliamo la derivata della funzione f(x) = senx.
Applichiamo la definizione di derivata:
lim
h0
f ( x  h)  f ( x )
h
Nel nostro caso f(x+h)= sen (x+h) e f(x) = senx pertanto:
f ( x  h)  f ( x )
sen( x  h)  sen( x)
 lim

h0
h0
h
h
Applichiamo le formule di addizione:
lim
 lim
h0
sen( x  h)  sen( x )
senx cos h  senh cos x  sen ( x )
 lim

h

0
h
h
Mettiamo sen x in evidenza:
 lim
h0
senx (cos h  1)  senh cos x
senx (cos h  1)
senh cos x
 lim
 lim
h0
h0
h
h
h
Riconosciamo 2 limiti notevoli:
senh
1  cosh
 1 lim
0
x 0
h
h
e x0
lim
Quindi:
0
 lim
h0
1
senx (cos h  1)
senh cos x
 lim
 cos x
h

0
h
h
D ( senx )  cos x
[email protected] | G.Grasso
6
www.matematicagenerale.it
[email protected] | G.Grasso