Le rappresentazioni e le proprietà dei numeri reali
In generale un numero qualsiasi, con sviluppo decimale finito o infinito, positivo, negativo o
nullo, è un numero relativo e appartiene all’insieme dei numeri reali.
La necessità di contare ha portato all’introduzione dei numeri naturali (ℕ), quella di
formalizzare gli scambi tra dare e avere ha dato origine alla creazione dei numeri interi (ℤ) e
la necessità di comparare una misura con un’unità di riferimento ha richiesto l’introduzione
dei numeri razionali (ℚ). Questi tre insiemi numerici sono uno contenuto nell’altro in base
alla seguente catena di inclusioni:
ℕ⊆ℤ⊆ℚ
In seguito, per rispondere alla necessità di utilizzare numeri che non è possibile rappresentare
come frazioni, sono stati introdotti i numeri reali (ℝ). L’insieme dei reali è dato dall’unione
dei numeri razionali e dei numeri irrazionali (𝕀), dove questi ultimi sono appunto definiti
come quei numeri reali che non possono essere scritti come frazioni.
ℝ =ℚ ∪𝕀
𝕀=ℝ−ℚ
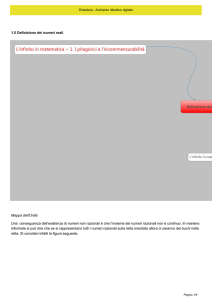
L’insieme dei numeri reali e i suoi sottoinsiemi possono venire rappresentati attraverso il
seguente diagramma di Eulero-Venn:
L’insieme 𝕀 contiene per esempio tutte le radici che danno come risultato numeri decimali
illimitati non periodici, ma anche numeri che non si ottengono dall’estrazione di radice come
π. Numeri di questo tipo sono chiamati trascendenti.
ESEMPIO
Vediamo la rappresentazione di alcuni numeri nell’insieme dei reali.
© Mondadori Education
Le proprietà dei numeri reali
I numeri naturali e i numeri interi possono venire rappresentati come punti su una retta
orientata, detta retta numerica. Gli insiemi ℕ e ℤ sono discreti: ciò significa che tra un
numero naturale (o intero) e il suo successore non ci sono altri numeri naturali (o interi).
Anche i numeri razionali si possono rappresentare geometricamente come punti su una retta. I
numeri razionali s’inseriscono tra quelli interi e non è possibile, per esempio, stabilire quale
sia il numero razionale più vicino a 1.
Inoltre l’insieme ℚ è denso: dal punto di vista matematico ciò significa che tra due numeri
razionali possiamo sempre inserire un altro numero razionale, per quanto vicini siano i numeri
scelti.
L’insieme dei numeri razionali è denso, ma non copre l’intera retta, cosa che avviene solo con
i numeri reali. Infatti i numeri reali possono essere messi in corrispondenza biunivoca con i
punti della retta, che viene appunto detta retta reale. L’insieme dei numeri reali risulta quindi
essere denso, come nel caso dei razionali, e in più continuo, in quanto a ogni punto sulla retta
corrisponde un numero reale.
Tutti gli insiemi numerici che abbiamo visto sono infiniti, ma hanno tra loro cardinalità
diverse. Gli insiemi ℕ, ℤ e ℚ hanno la stessa cardinalità, e in base a questo vengono definiti
insiemi numerabili, mentre l’insieme dei numeri reali ℝ non è numerabile ma ha una
cardinalità maggiore.
L’insieme dei numeri reali ℝ è infinito, ordinato, denso e continuo.
All’interno dell’insieme dei reali valgono tutte le proprietà e le operazioni introdotte negli
altri insiemi numerici, e in particolare tutte le operazioni definite per i razionali.
Le operazioni di somma e prodotto tra numeri reali godono delle seguenti proprietà:
Commutatività: 𝑎 + 𝑏 = 𝑏 + 𝑎, 𝑎 ⋅ 𝑏 = 𝑏 ⋅ 𝑎
Associatività: 𝑎 + (𝑏 + 𝑐) = (𝑎 + 𝑏) + 𝑐, 𝑎 ⋅ (𝑏 ⋅ 𝑐) = (𝑎 ⋅ 𝑏) ⋅ 𝑐
Elemento neutro: 0 rispetto alla somma (𝑎 + 0 = 𝑎) e 1 rispetto al prodotto (𝑎 ⋅ 1 = 𝑎)
Proprietà distributiva del prodotto rispetto alla somma: 𝑎 ⋅ (𝑏 + 𝑐) = 𝑎 ∙ 𝑏 + 𝑎 ∙ 𝑐
© Mondadori Education
Come nel caso dei numeri interi, anche per un qualsiasi numero reale il segno positivo si può
1 1
sottintendere. Le scritture + e sono equivalenti, così come +√4 e √4.
2 2
Per indicare un generico numero reale utilizzeremo le lettere minuscole (a, b, c,...) ma, a
differenza dei numeri reali assoluti, la lettera può rappresentare un numero positivo, negativo
o nullo:
𝑎 = +5,
𝑏 = −2,
𝑐=0
L’approssimazione dei numeri reali
La rappresentazione di questi numeri in ambito applicativo, come per esempio in informatica,
economia, fisica o ingegneria, è necessariamente approssimata. Qualsiasi strumento di
calcolo ha a disposizione solo un numero finito di cifre e non è possibile inserire in un
programma informatico numeri reali troppo grandi o troppo piccoli. Nessun elaboratore è,
infatti, in grado di rappresentare un numero reale, ma ricorre a una sua approssimazione,
utilizzando una parte intera e una frazionaria.
Per questo motivo in informatica esistono due modi di rappresentare i numeri reali:
virgola fissa;
virgola mobile.
La rappresentazione in virgola fissa si presta bene a rappresentare numeri frazionari non
molto grandi e non molto piccoli. Una parte è dedicata alla porzione intera e una parte a
quella decimale, e la posizione della virgola è fissata.
Per i numeri reali si preferisce la rappresentazione in virgola mobile, indicata come floating
point, che ovvia ai limiti della rappresentazione in virgola fissa e deriva dalla notazione
scientifica. La rappresentazione in virgola mobile consente di estendere l’intervallo di numeri
rappresentati, a parità di cifre, rispetto alla notazione in virgola fissa.
ESEMPIO
La massa di un elettrone non è rappresentabile facilmente in virgola fissa, dove è fissato il
numero di cifre intere e decimali a priori, ma lo è in notazione esponenziale.
0,000000000000000000000000000000091 kg = 9,1 ∙ 10−31
© Mondadori Education
Mettiti alla prova
1. In quale insieme è sempre possibile operare con l’operazione di divisione?
Nell’insieme dei numeri naturali.
Nell’insieme dei numeri razionali.
Nell’insieme dei numeri interi.
In nessuno degli insiemi precedenti.
Rappresenta sulla retta i seguenti numeri interi.
2. −4; 2; −3; 3; −6; 1
3. −1; 4; −5; 5; 6; −2
Rappresenta sulla retta i seguenti numeri razionali.
4.
5.
3
3
5
7
2
− ;
;
2
1
− ;
2
− ;
4
2
5
7
4
4
− ;
9
5
− ;
;
;
−
3
3
4
4
− ;
;
1
4
−
11
4
© Mondadori Education
6. Indica le caratteristiche attribuibili all’insieme ℚ.
È denso.
È completo.
Non è completo.
Non è denso.
7. Indica le caratteristiche attribuibili all’insieme ℝ.
È denso.
È completo.
Non è completo.
Non è denso.
Attribuisci all’insieme corretto i seguenti numeri reali.
8. −3
9. −0,01
7
3
+0, 1̅
0, 2̅
−√4
√3
21
−4
−
−
4
3
1
5
−√5
0
−2,5
−0, 3̅
√4
−11
√50
−√10
1
8
© Mondadori Education
10. Realizza una tabella a tre colonne. Nella prima colonna inserisci i numeri da 1 a 20, nella
seconda indica la radice quadrata del valore presente nella prima colonna e nella terza
colonna indica la radice cubica del valore dato nella prima colonna. Cerchia i radicali che
hanno il risultato in ℕ.
𝒏
√𝒏
𝟑
1
√1
3
2
√2
3
…
…
…
√𝒏
√1
√2
11. Quanti numeri razionali è possibile inserire tra −0,01 e +0,01?
1
100
Nessuno
Infiniti
12. Quali dei seguenti radicali appartengono all’insieme ℚ?
√5
3
√27
4
√
9
√10
3
√√1
13. Inserisci in un programma per la geometria dinamica i seguenti punti a coordinate reali e
riscrivi in ordine crescente i numeri. In alternativa utilizza una retta da te costruita.
𝐴 = (π; 0)
5
𝐵 = (− ; 0)
3
𝐷 = (−√7, ; 0)
7
𝐸 =( ; 0)
3
𝐹 = (−√2; 0)
𝐺 = (−1,5; 0)
𝐻 = (√6; 0)
𝐼=(
√4
; 0)
3
𝐿 = (−2,9; 0)
Quali tra le seguenti relazioni sono vere?
14.
ℚ⊆ℤ
ℕ⊆ℤ
ℝ⊆ℚ⊆ℤ⊆ℕ
ℝ⊆ℚ⊆ℤ⊆ℕ
© Mondadori Education
15.
√2 ∈ ℤ
−2 ∈ ℤ
2∉ℤ
1
−3 ∈ ℚ
16.
0, 3̅ ∈ ℚ
1
−3 ⊆ ℤ
𝜋⊆ℚ
0,2 ⊆ ℤ
Scrivi i seguenti numeri in notazione scientifica.
17. a. Dimensione dei cromosomi: 0,0000001 m
b. Massa al lancio dello Space Shuttle: 2 040 000 kg
18. a. Densità dell’atmosfera a 68 km di altitudine: 0,000109 kg/m3
b. Stima della produzione di petrolio nel 2001: 45 000 000 000 l
19. a. Spessore del filo di una ragnatela: 0,000007 m
b. Massa della piramide di Giza: 6 000 000 kg
20. a. Probabilità a poker di avere nella prima mano una scala reale: 0,0000015
b. Massa della Luna: 7 349 000 000 000 000 000 000 kg
© Mondadori Education