Richiami di teoria delle probabilità

RICHIAMI DI TEORIA DELLE PROBABILITA’
Classificando i segnali, all’inizio del Corso, si è fatta distinzione tra segnali determinati e segnali
aleatori. Per lo studio di questi ultimi è indispensabile richiamare alcuni concetti del calcolo
probabilistico e della teoria delle variabili aleatorie. Ciò viene fatto nella presente dispensa in cui,
senza alcuna pretesa di completezza, verranno ricordate alcune definizioni “classiche” e forniti
esempi di distribuzioni statistiche che, a vario titolo e con varie modalità, saranno utili per
proseguire nello studio.
Cominciamo con il ricordare la definizione di esperimento aleatorio: si definisce tale un “evento” di
qualunque natura e consistenza, il cui risultato non è certo a priori ma può assumere una serie di
esiti caratterizzati da un valore di probabilità. Per citare esempi ben noti, il lancio di una moneta è
un esperimento aleatorio in quanto non è dato di sapere a priori quale sarà l’esito del lancio; ciò che
si sa a priori è che, se la moneta non è truccata, la probabilità che esca una delle due facce è del
50%. Analogamente, quale risultato del lancio di un dado, la probabilità di ottenere il 4 (ma lo
stesso vale per qualunque altra faccia) è del 16.66% (100/6%).
Anche un segnale aleatorio può essere riguardato come il risultato di un esperimento aleatorio. Un
segnale
s (t ) = A cos(2π f0t + ϕ )
(1)
in cui A (ampiezza) ed f0 (frequenza) sono quantità determinate mentre ϕ può assumere, con la
stessa probabilità, un qualunque valore compreso tra 0 e 2π, è un segnale aleatorio 1 e ripetendo
l’esperimento di generazione del segnale un numero arbitrario di volte, con istante di accensione
generico dell’oscillatore che produce il segnale stesso, è lecito attendersi che il valore di ϕ possa
essere diverso ogni volta.
Ogni esperimento aleatorio può dunque fornire una serie di risultati. In molti casi questi risultati
sono già in forma numerica (si pensi al lancio del dado). Per gli altri, nulla impedisce di associare
ad ogni possibile esito dell’esperimento un numero. Si pensi al lancio della moneta: si può far
corrispondere ad uno dei due possibili esiti il numero 1, e all’altro esito il numero 2. Così facendo si
associa all’esperimento aleatorio una variabile che, con ovvio significato del termine, prende il
nome di variabile aleatoria. La variabile aleatoria può essere:
- discreta quando l’insieme dei valori che essa assume è discreto;
- continua quando l’insieme dei valori che essa assume è continuo.
Le variabili aleatorie associate al lancio del dado o della moneta sono, evidentemente, esempi di
variabili discrete; la variabile ϕ che compare nella (1) è invece un esempio di variabile aleatoria
continua, in quanto può assumere, per ipotesi, qualunque valore reale compreso tra 0 e 2π. In alcuni
casi si hanno esempi di variabili aleatorie miste, in cui alcuni valori (discreti) sono più “importanti”
degli altri; il senso di questa affermazione risulterà chiaro successivamente.
Spesso, a livello di notazione, per indicare la variabile aleatoria si utilizzano le lettere maiuscole,
mentre le lettere minuscole stanno ad indicare un particolare esito dell’esperimento aleatorio (si
parla di realizzazione o determinazione). Così, nell’esempio fornito dalla (1), la variabile aleatoria
viene indicata con Φ, mentre scrivere che Φ = ϕ significa che la variabile aleatoria ha assunto, a
seguito dell’esperimento, il particolare valore ϕ.
Da quanto precede risulta evidente che a ciascuno dei valori possibili per la variabile aleatoria è
associato un numero il quale esprime la probabilità che si ottenga proprio tale valore come risultato
dell’esperimento. Oltre che i singoli risultati di un esperimento, è spesso importante considerare
anche dei gruppi di risultati. Si consideri l’esperimento aleatorio che consiste nel contare il numero
di persone che, in un ben determinato intervallo della giornata, si presentano alla cassa di un
supermercato. Questo è un esperimento aleatorio, in quanto non è dato sapere a priori quale sarà tale
1
L’aleatorietà è localizzata nel parametro ϕ; in casi come questo, si parla allora di “aleatorietà parametrica”.
1
numero. Accanto alla conoscenza del valore assoluto del numero delle persone, si può essere
interessati a conoscere, ad esempio, quale sia la probabilità che il numero di clienti nell’intervallo
temporale considerato sia maggiore di 20. L’interesse nell’esperimento potrebbe allora essere
concentrato sul seguente evento: numero di clienti superiore a 20, nel qual caso i valori di interesse
della variabile aleatoria, detta X, sarebbero solo quelli che soddisfano tale condizione, e cioè 21, 22,
23, …. Analogamente, a partire dallo stesso esperimento aleatorio si possono chiaramente definire
molti altri eventi.
Indicato dunque con Ω l’insieme complessivo dei valori possibili (tale insieme si chiama spazio
campione) gli eventi sono sottoinsiemi dello spazio campione che verificano le seguenti condizioni:
1. se A è un evento, anche il suo complemento A , rispetto all’insieme Ω, è un evento;
2. se A e B sono eventi, anche la loro unione A ∪ B è un evento;
3. se A e B sono eventi, anche la loro intersezione A ∩ B è un evento;
4. dato un evento A, gli insiemi A ∪ A e A ∩ A sono (particolari) eventi: il primo coincidente
con Ω (ovvero con lo spazio campione), è detto evento certo, mentre il secondo, indicato
con il simbolo ∅ e non contenente alcun risultato dell’esperimento, è detto evento
impossibile.
Le condizioni enucleate meritano qualche commento. In primo luogo va detto che le condizioni 3 e
4 sono, in realtà conseguenza delle (e si dimostrano dunque a partire dalle) condizioni 1 e 2. Per
complemento A dell’evento A si intende l’evento che considera i valori dello spazio campione non
considerati da A. Nell’esempio della cassa del supermercato, l’evento complementare a quello sopra
considerato, e cioè: numero di clienti superiore a 20, sarà: numero di clienti minore o uguale a 20.
L’unione ∪ di due eventi A e B considera i risultati di interesse per A o per B (non necessariamente
comuni ad entrambi). L’intersezione ∩ di due eventi A e B considera i risultati di interesse per A e
per B (solo quelli comuni ad entrambi). A partire da queste definizioni, la condizione 4, in
particolare risulta ovvia: l’unione di due eventi complementari restituisce la totalità dei valori
possibili, e dunque lo spazio campione, mentre l’intersezione di due eventi complementari non ha
elementi in comune. Anche il singolo risultato dell’esperimento è, chiaramente, un evento, quello
che consiste nella considerazione di un particolare risultato.
A partire da queste definizioni, come gli esempi introduttivi già mettevano in evidenza, dato un
esperimento aleatorio, occorre associare ad ogni possibile evento un valore di probabilità.
Formalmente questa operazione, che potrebbe apparire banale alla luce dell’uso, spesso improprio,
che del concetto di probabilità siamo soliti fare nella vita quotidiana, è tutt’altro che semplice.
Senza voler richiamare concetti complessi, inappropriati per la presente trattazione, verranno
proposte di seguito tre diverse (anche se, chiaramente, correlate) formulazioni.
Teoria assiomatica di Kolmogorov
Secondo questo approccio, assegnato un esperimento aleatorio con uno spazio campione Ω e
l’insieme degli eventi ad esso relativi, detto classe degli eventi ed indicato con S, una legge di
probabilità Pr{⋅} è una corrispondenza che associa ad ogni elemento di S, e quindi ad ogni evento di
interesse in una prova dell’esperimento, un numero reale che soddisfa i seguenti assiomi 2 :
A.1 – la probabilità di un evento arbitrario A è non negativa, si ha cioè:
Pr { A} ≥ 0
(2)
A.2 – la probabilità dell’evento certo è unitaria (assioma di normalizzazione), si ha cioè:
Pr {Ω} = 1
2
(3)
In quanto assiomi, essi non devono essere dimostrati.
2
A.3 – dati due eventi A e B mutuamente esclusivi (ovvero incompatibili, cioè tali che non possano
verificarsi contemporaneamente) la probabilità dell’evento unione è data dalla somma delle
probabilità dei singoli eventi, si ha cioè:
A ∩ B = ∅ → Pr { A ∪ B} = Pr { A} + Pr { B}
(4)
Da questi assiomi si ricavano poi alcune proprietà che sembrano ovvie, ma che devono comunque
essere ricondotte ai principi primi (e cioè gli assiomi A.1 – A. 3):
-
dato un evento A, la probabilità dell’evento complementare A è data dal complemento a 1
della Pr{A}, si ha cioè:
Pr { A} = 1 − Pr { A}
-
(5)
l’insieme impossibile ha probabilità nulla di verificarsi, si ha cioè:
Pr {∅} = 0
-
(6)
la probabilità di un evento A non può assumere un valore maggiore di 1, si ha cioè:
0 ≤ Pr { A} ≤ 1
-
(7)
dati due eventi A e B, la probabilità dell’evento unione A ∪ B è espressa dall’uguaglianza:
Pr { A ∪ B} = Pr { A} + Pr { B} − Pr { A ∩ B}
(8)
Data una coppia di eventi A e B la probabilità dell’evento intersezione, spesso indicata
semplicemente con Pr{A, B}, è detta probabilità congiunta, mentre Pr{A} e Pr{B} hanno il
significato di probabilità marginali. Data una coppia di eventi A e B con Pr{B} ≠ 0, si definisce poi
la probabilità condizionata:
Pr { A | B} =
Pr { A, B}
(9)
Pr { B}
la quale esprime la probabilità dell’evento A condizionata al verificarsi dell’evento B (che ha
dunque il significato di evento condizionante).
Un modo semplice, ma convincente, per memorizzare (ma anche giustificare) le proprietà sopra
elencate, consiste nell’utilizzo dei diagrammi di Venn, largamente usati, come ben noto, nella teoria
degli insiemi. In Figura 1, il rettangolo rappresenta l’evento certo Ω, A è un generico evento e A il
suo complementare. Dalla Figura 2 può invece essere giustificato il risultato (8). L’evento A ∪ B è
rappresentato dalla sovrapposizione dei diagrammi di A e di B; sommando, semplicemente, le
Pr{A} e Pr{B}, la probabilità di A ∩ B verrebbe conteggiata due volte. E’ dunque necessario
toglierla per ricavare la probabilità dell’unione. La probabilità dell’unione diventa uguale alla
somma delle probabilità degli eventi singoli nel caso in cui essi siano disgiunti in quanto, come tali,
essi non hanno elementi in comune (Figura 3).
3
A
A
Ω
Figura 1
A
B
Ω
Figura 2
A
B
Ω
Figura 3
Definizione “classica” di probabilità
In accordo con questa definizione, storicamente attribuita a Laplace, la Pr{A} si calcola:
- individuando il numero NF(A) dei cosiddetti casi favorevoli ad A,
- individuando il numero NP dei cosiddetti casi possibili,
- dividendo NF(A) per NP.
In formula:
Pr { A} =
N F ( A)
NP
(10)
In pratica: NP è il numero totale dei risultati contenuti in Ω, mentre NF(A) è il numero di risultati
contenuti in A. E’ applicando questa definizione che, ad esempio, si ricava che la probabilità che si
verifichi l’evento A = {il risultato del lancio del dado è 4} è Pr{A} = 1/6; si ha infatti NP = 6 e NF(A)
= 1. D’altro canto possiamo definire un diverso evento B = {il risultato del lancio del dado è un
numero pari}, ottenendo Pr{B} = 1/2 in quanto, per quest’altro evento, i casi favorevoli sono 3
(sempre sul totale di 6 casi possibili).
4
In effetti, la definizione classica di probabilità viene applicata di frequente nella pratica, anche in
virtù della sua semplicità. Nondimeno, è facile convincersi che essa presuppone una ipotesi
“chiave”: la perfetta “simmetria” dell’esperimento (nel caso del dado la effettiva simmetria dello
stesso) ovvero, più chiaramente, l’equiprobabilità di tutti i risultati dell’esperimento. Se questa
ipotesi non è verificata, l’applicabilità della (10) viene meno. La definizione “classica”, ad esempio,
non è utilizzabile nel caso di dado truccato (e dunque non simmetrico) quando la probabilità di
avere in uscita le varie facce non è identica per tutte le facce.
Definizione “frequentista” di probabilità (di Von Mises)
Questa definizione è simile a quella classica ma, rispetto a quest’ultima, ha il vantaggio di poter
essere applicata anche nel caso di esperimento non simmetrico (nel senso precisato più sopra: ad
esempio per un dado truccato). Di nuovo si esprime la probabilità come un rapporto ma, in questo
caso, le quantità a numeratore e denominatore sono ricavate sperimentalmente. In sostanza,
dovendo calcolare la probabilità di un evento A:
- si ripete l’esperimento aleatorio un numero N di volte,
- si conta il numero di volte NA in cui l’esperimento ha dato un esito favorevole ad A,
- si divide NA per N.
Il punto rilevante è che il rapporto così ottenuto approssima la probabilità di errore corretta solo a
patto di considerare un numero di ripetizioni dell’esperimento sufficientemente elevato (al limite,
tendente all’infinito). Si deve cioè porre:
NA
N →∞ N
Pr { A} = lim
(11)
Il senso del passaggio al limite è, ancora una volta, chiaro anche solo pensando ai semplici esempi
mutuati dall’esperienza quotidiana. Dal lancio ripetuto di una moneta non truccata si può stimare
che la probabilità che si abbia come risultato una faccia è uguale a 1/2 solo effettuando un numero
molto elevato di lanci, poiché è certamente possibile che, in una serie limitata, si abbia l’uscita,
sistematica e costante, di una sola delle due facce. Peraltro, come detto, la (11) ha il vantaggio
(concettuale) di poter essere applicata anche nel caso di moneta truccata. Ovviamente, il passaggio
al limite resta, essenzialmente, un’astrazione matematica, ragion per cui non sono rari i casi in cui
l’uso della (11) fornisce solo un’approssimazione della probabilità cercata. Ovviamente, nei casi in
cui si è convinti della simmetria dell’esperimento (e dunque dell’equiprobabilità dei risultati) è
conveniente ed opportuno l’uso della (10), assai più semplice da calcolare.
E’ anche importante evidenziare che la definizione frequentista non è in contrasto con quella
assiomatica di Kolmogorov. Infatti, la probabilità Pr{A}, espressa dalla (11), è:
i)
una quantità non negativa, poiché prodotta dal limite di un rapporto fra quantità positive;
ii)
se l’evento A coincide con Ω, allora banalmente si ha NA = N e quindi Pr{A} = 1;
iii)
se A e B sono due eventi che si escludono vicendevolmente (mutuamente esclusivi),
allora una prova dell’esperimento che fa verificare A ∪ B dà un risultato che sta in A o in
B, ma che non può stare in entrambi; ne consegue che NA∪B = NA + NB e quindi
N A∪ B
N + NB
N
N
= lim A
= lim A + lim B = Pr { A} + Pr { B}
N →∞ N
N →∞
N →∞ N
N →∞ N
N
Pr { A ∪ B} = lim
Gli assiomi A.1-A.3 sono dunque tutti automaticamente verificati (e con essi anche le proprietà
conseguenti).
Diamo ora la definizione di eventi statisticamente indipendenti:
5
Due eventi A e B sono indipendenti se il verificarsi dell’uno non ha alcuna implicazione sul
verificarsi dell’altro. Ricordando la precedente definizione di probabilità condizionata, ciò implica,
ad esempio che la probabilità marginale Pr{A} e la probabilità condizionata Pr{A|B} sono identiche:
Pr { A} = Pr { A | B}
(12)
per eventi indipendenti
Ovviamente è anche vero che:
Pr { B} = Pr { B | A}
(13)
per eventi indipendenti
Ricordando la (9), si può allora concludere che, per eventi indipendenti:
Pr { A, B} = Pr { A} ⋅ Pr { B}
(14)
e cioè che la probabilità congiunta è uguale al prodotto delle probabilità marginali (dei singoli
eventi).
Un altro importante risultato è il teorema (o formula) di Bayes, che può essere formalizzato nel
modo seguente:
Pr { A | B} =
Pr { B | A} ⋅ Pr { A}
(15)
Pr { B}
La formula di Bayes è spesso usata in combinazione con il teorema della probabilità totale, che
esaminiamo di seguito.
Costruiamo, preliminarmente, una partizione dello spazio Ω scegliendo N eventi Bi (con i = 1, 2, …,
N) di S con le seguenti proprietà (che, di fatto, costituiscono la definizione stessa di partizione):
Bi ∩ Bk = ∅ se i ≠ k
(16a)
N
∪ Bi = Ω
(16b)
i =1
La (16a) esprime il fatto che gli elementi della partizione sono disgiunti, mentre la (16b) esprime il
fatto che l’unione di tutti gli eventi della partizione restituisce lo spazio campione. Un esempio di
partizione è mostrato in Figura 4.
B
B
A
B
B
Ω
B
B
B
Figura 4
6
Nella stessa figura, peraltro, è anche rappresentato un generico evento A, che non è un elemento
della partizione. Ricordando l’assioma A.3 si può scrivere:
N
N
⎧⎪
⎫⎪
⎧⎪ N
⎫⎪ N
Pr { A} = Pr { A ∩ Ω } = Pr ⎨ A ∩ ∪ Bi ⎬ = Pr ⎨∪ A ∩ Bi ⎬ = ∑ Pr { A ∩ Bi } = ∑ Pr { A | Bi } ⋅Pr { Bi } (17)
⎪⎩
⎪⎩i =1
⎪⎭ i =1
i =1
i =1 ⎪
⎭
Quest’ultima espressione costituisce, appunto, l’enunciato del teorema della probabilità totale.
Se ora si riscrive la (15), con un cambio di notazione come:
Pr {Bi | A} =
Pr { A | Bi } ⋅ Pr { Bi }
(18)
Pr { A}
sostituendo la (17) si ottiene:
Pr { Bi | A} =
Pr { A | Bi } ⋅ Pr { Bi }
(19)
N
∑ Pr { A | Bi } ⋅Pr {Bi }
i =1
che è, in effetti, formula ampiamente utilizzata nella pratica.
*****
Esperimento di Bernoulli
Quanto precede è sufficiente per introdurre un esperimento aleatorio di grande importanza nella
pratica: le cosiddette prove di Bernoulli (o prove ripetute binarie e indipendenti).
Si definisce tale un esperimento aleatorio a due soli esiti, indicati con x1 e con x2 caratterizzati da:
Pr { x1} = p
(20a)
Pr { x2 } = q = 1 − p
(20b)
Si considerano n ripetizioni dell’esperimento assicurandosi che la singola ripetizione non abbia
alcuna relazione con le altre (ipotesi di indipendenza) e si considera l’evento A = {x1 si è presentato
k volte nelle n prove ripetute}. In virtù dell’indipendenza, applicando ripetutamente il risultato (14)
all’evento A ed il suo complementare A , si trova immediatamente:
()
n!
Pr { A} = n p k q n −k =
p k (1 − p ) n−k
k
k !(n − k )!
(20)
Nella (20), pkqn−k esprime il fatto che sono favorevoli all’evento A i casi in cui x1 si è presentato k
volte e, conseguentemente, x2 si è presentato (n − k) volte, mentre il coefficiente binomiale n
k
tiene conto del numero di tali casi, potendosi disporre, nella sequenza delle repliche
dell’esperimento, i k valori x1 in un numero di modi che uguaglia le combinazioni semplici di classe
k di n elementi. La (20) è nota come formula di Bernoulli.
()
*****
7
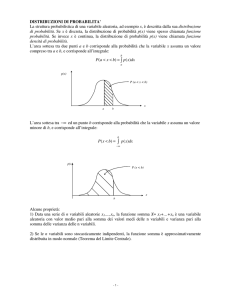
Distribuzione di probabilità cumulativa e densità di probabilità
In molti contesti di interesse pratico si pone il problema di calcolare la probabilità che una variabile
aleatoria X assuma valori all’interno di un dato intervallo (a, b] 3 , vale a dire la Pr{a < X ≤ b}. E’
chiaro, riprendendo la notazione precedente, che la scrittura a < X ≤ b identifica un evento: quello
che è soddisfatto dai risultati dello spazio campione che verificano la condizione posta sulla
variabile aleatoria.
Per risolvere un problema di questo tipo, risulta utile la seguente definizione di distribuzione di
probabilità cumulativa (o funzione di ripartizione):
FX ( x ) = Pr { X ≤ x}
(21)
FX(x) esprime dunque la probabilità che la variabile aleatoria X assuma valori non maggiori del
valore, x, assegnato. E’ evidente che FX(x) deve soddisfare le seguenti proprietà:
D.1 – assume valori appartenenti all’intervallo [0, 1], cioè:
0 ≤ FX ( x) ≤ 1
(22)
D.2 – il suo valore limite, per x → ∞, è uguale a 1, cioè:
lim FX ( x) = FX (∞) = Pr { X ≤ ∞} = 1
(23)
x →∞
D.3 – il suo valore limite, per x → −∞, è uguale a 0, cioè:
lim FX ( x) = FX ( −∞) = Pr { X ≤ −∞} = 0
x →−∞
(24)
D.4 – è monotona non decrescente, cioè:
x2 > x1 ⇒ FX ( x2 ) ≥ FX ( x1 )
(25)
D.5 – se presenta una discontinuità di prima specie 4 , nel punto x = x , allora la differenza tra il suo
limite destro e il suo limite sinistro in tale punto è pari alla probabilità dell’evento X = x , cioè:
Pr { X = x } = FX ( x + ) − FX ( x − )
(26)
avendo indicato con FX ( x + ) il limite destro e con FX ( x − ) quello sinistro.
Tutte le proprietà precedenti sono ovvie, o comunque facilmente verificabili. In particolare, la
proprietà D.2 deriva dal fatto che l’evento X ≤ ∞ coincide con l’evento certo Ω; dualmente, la
proprietà D.3 deriva dal fatto che l’evento X ≤ −∞ coincide con l’evento impossibile ∅.
Utilizzando la definizione di FX(x), è chiaro che si può scrivere:
Pr {a < X ≤ b} = Pr { X ≤ b} − Pr { X ≤ a} = FX (b) − FX (a )
(27)
Si ricordi che la notazione (⋅, ⋅] indica un intervallo aperto a sinistra e chiuso a destra.
Si ricordi che una funzione presenta in un punto una discontinuità di prima specie se in quel punto la funzione ha un
“salto”, con limite destro e sinistro ambedue finiti ma diversi tra loro.
3
4
8
la quale risolve il problema iniziale.
Peraltro, lo stesso problema del calcolo della Pr{a < X ≤ b} può essere affrontato e risolto
utilizzando un’altra funzione, legata alla precedente, la cosiddetta funzione densità di probabilità,
così definita:
f X ( x) =
dFX ( x)
dx
(28)
Dalla (28) si ricava immediatamente la relazione inversa:
x
FX ( x) =
∫
f X (ξ )dξ
(29)
−∞
Anche la densità di probabilità deve soddisfare alcune proprietà; in particolare:
DD.1 – è una funzione non negativa, cioè:
f X ( x) ≥ 0
(30)
DD.2 – il suo integrale esteso all’intero asse reale è uguale a 1, cioè:
∞
∫
f X ( x)dx = 1
(31)
−∞
La proprietà DD.2 per la densità di probabilità, è conseguenza della proprietà D.2 per la
distribuzione di probabilità cumulativa; ambedue sono manifestazioni dell’assioma A.2 (di
normalizzazione) della formulazione assiomatica. La (31) costituisce il primo fondamentale passo,
ove si debba verificare se una assegnata funzione fX(x) rappresenta o meno una densità di
probabilità, ovvero, sotto quali condizioni lo diventa, ad esempio tramite una scelta appropriata di
uno o più parametri, da cui essa dipende. Per chiarire quest’ultimo concetto, si guardi, ad esempio,
alla Figura 5; in essa è rappresentata una funzione costante che, per essere una densità di
probabilità, deve avere ampiezza pari a 1/(b – a); solo in questo caso, infatti, la condizione di
normalizzazione (31) è verificata.
fX (x)
a
b
Figura 5
9
x
Utilizzando la fX(x), la Pr{a < X ≤ b} può essere calcolata come segue:
Pr {a < X ≤ b} = FX (b) − FX (a) =
b
∫
a
f X ( x)dx −
−∞
∫
−∞
b
f X ( x)dx = ∫ f X ( x)dx
(32)
a
All’inizio della trattazione si è detto che una variabile aleatoria può essere: discreta, quando
l’insieme dei valori che essa assume è discreto; continua, quando l’insieme dei valori che essa
assume è continuo. Per come sono definite, la distribuzione di probabilità cumulativa e la densità di
probabilità sembrano “naturalmente” adattarsi al caso di variabile continua. Nondimeno, è facile
convincersi che esse possono essere applicate anche al caso di variabile discreta, per la quale
assumono andamenti “caratteristici”.
Per quanto riguarda la distribuzione di probabilità cumulativa, si tratta di una funzione che rimane
costante nei tratti che separano due generici valori possibili, e che si incrementa in corrispondenza
di ciascuno di questi valori, per una quantità pari alla probabilità che lo caratterizza. In Figura 6, ad
esempio, è mostrata la distribuzione di probabilità cumulativa dell’esperimento aleatorio del lancio
del dado: la funzione si incrementa, di una quantità pari a 1/6, in corrispondenza dei valori 1, 2, …,
6, che corrispondono alle 6 facce del dado.
FX (x)
1
5/6
4/6
3/6
2/6
1/6
0
1 2 3 4
5
6
x
Figura 6
Generalizzando, la distribuzione di probabilità cumulativa per una variabile discreta è una funzione
a gradini (costante a tratti), esprimibile come segue:
FX ( x) = ∑ Pr { X = xk } u ( x − xk )
(33)
k
dove gli xk sono i valori possibili e u(x – xk) è il gradino unitario che parte da xk.
Per quanto riguarda la densità di probabilità di una variabile aleatoria discreta, essa, in senso stretto,
sembrerebbe non definibile, visto che la (33) non è derivabile. Il problema può però essere aggirato,
in modo analogo a quanto si è fatto, ad esempio, per la trasformata di Fourier, utilizzando l’impulso
matematico (delta di Dirac). Esso consente di usare la (28), a partire dalla (33), ottenendo per una
generica variabile discreta:
f X ( x) = ∑ Pr { X = xk } δ ( x − xk )
(34)
k
10
La densità di probabilità di una variabile discreta è dunque data da una sequenza di delta di Dirac,
centrate sui valori possibili della variabile e di area pari alla corrispondente probabilità. La densità
di probabilità associata all’esperimento aleatorio del lancio del dado è mostrata in Figura 7.
fX (x)
0
1 2 3 4
5 6
x
Figura 7
Altri esempi di distribuzioni di probabilità cumulativa sono riportati in Figura 8 con, in Figura 9, le
corrispondenti densità di probabilità. Le Figure 8(a) e 9(a) si riferiscono al caso di variabile
aleatoria continua. Le Figure 8(b) e 9(b) sono invece relative al caso di variabile aleatoria discreta,
appena discusso. Interessanti sono anche le Figure 8(c) e 9(c), che si riferiscono a una variabile
aleatoria mista.
Nel caso di variabile aleatoria continua, la probabilità che la X assuma un particolare valore x è
uguale a zero. Questa conclusione è banale conseguenza del fatto che risulta (dalla (32)):
Pr { x < X ≤ x + Δ x} =
x +Δx
∫
f X ( x)dx
(35)
x
Se Δx è molto piccolo, questa espressione può essere approssimata con:
Pr { x < X ≤ x + Δ x} ≈ f X ( x )Δ x
(36)
che facendo tendere Δx a zero, visto che f X ( x ) assume necessariamente un valore finito, dà come
risultato:
Pr { X = x } = 0
(37)
Nel caso di variabile discreta, la stessa conclusione vale per tutti i valori di X non ammissibili,
mentre in corrispondenza dei valori ammissibili xk si ha, come già detto:
lim Pr { xk < X ≤ xk + Δ x} = Pr { X = xk }
(38)
Δ x →0
Ciò è del resto congruente con la (34), visto che, per Δx prossimo a zero, si ha:
11
Pr { xk < X ≤ xk + Δ x} =
xk + Δ x
∫
Pr { X = xk } δ ( x − xk )dx
(39)
xk
Nel caso di Figura 8(c) e 9(c) la variabile aleatoria è quasi ovunque continua (e dunque vale, quasi
ovunque, la (37)) ma il valore x1 (e solo quello) ha una probabilità diversa da zero di verificarsi. Di
qui discende il nome di variabile aleatoria mista, cioè caratterizzata dalla coesistenza di una parte
continua e di una parte discreta.
Figura 8
12
Figura 9
*****
Esempi di variabili aleatorie
Si forniscono, di seguito alcuni esempi di variabili aleatorie “classiche”, molto importanti per le
applicazioni. Per comodità (e anche in considerazione del fatto che la terminologia è di solito
coerente con questa scelta) il punto di partenza è costituito dalla densità di probabilità, donde è
facile, utilizzando la (29), ricavare la distribuzione di probabilità cumulativa.
Variabile uniforme
Si tratta di una variabile aleatoria continua caratterizzata dalla densità di probabilità:
⎧ 1
⎪
f X ( x) = ⎨ b − a
⎪0
⎩
a≤ x≤b
(40)
x < a, x > b
Per integrazione si ottiene:
⎧ 0
⎪
⎪x−a
FX ( x) = ⎨
⎪b − a
⎪ 1
⎩
x<a
a≤ x≤b
(41)
x>b
13
Esponenziale unilatera
Si tratta di una variabile aleatoria continua caratterizzata dalla densità di probabilità:
⎧⎪a ⋅ exp(−ax)
f X ( x) = ⎨
⎪⎩0
x≥0
(42)
x<0
con a > 0.
Per integrazione si ottiene:
⎧⎪1 − exp(−ax)
FX ( x) = ⎨
0
⎪⎩
x≥0
(43)
x<0
Esponenziale bilatera (di Laplace)
Si tratta di una variabile aleatoria continua caratterizzata dalla densità di probabilità:
f X ( x) =
a
exp ( −a x )
2
(44)
con a > 0.
Per integrazione si ottiene:
⎧ 1
⎪ 2 exp(ax)
⎪
FX ( x) = ⎨
⎪ 1
⎪⎩1 − 2 exp(−ax)
x<0
(45)
x≥0
Gaussiana
Si tratta di una variabile aleatoria continua caratterizzata dalla densità di probabilità:
f X ( x) =
⎡ ( x − μ )2 ⎤
1
exp ⎢ −
⎥
2πσ
2σ 2 ⎥⎦
⎢⎣
(46)
(il significato dei parametri μ e σ risulterà chiaro successivamente).
L’integrale della (46), necessario per il calcolo della distribuzione di probabilità cumulativa è,
almeno apparentemente, non banale. Nondimeno è tale la sua importanza che gran parte dei
software di calcolo in commercio mette a disposizione funzioni esplicite per la sua valutazione. In
alternativa, sono disponibili tabelle che la stessa informazione forniscono con un prefissato passo di
discretizzazione dell’argomento.
In dettaglio:
1
FX ( x) =
2πσ
⎡ (ξ − μ ) 2 ⎤
exp
∫ ⎢⎢ − 2σ 2 ⎥⎥dξ
⎣
⎦
−∞
x
(47)
Introducendo il cambiamento di variabile:
14
y=
(ξ − μ )
2σ
→ dξ = 2σ dy
(48)
la (47) diventa:
FX ( x) =
1
π
x−μ
2σ
∫
( )
exp − y 2 dy
−∞
(49)
Si consideri ora la seguente definizione di funzione erfc(x) (funzione errore complementare):
erfc( x) =
2
π
∞
∫ exp ( − y
2
)dy
(50)
x
Tale funzione verifica le seguenti proprietà:
erfc(−∞) = 2
erfc(0) = 1
(51)
Si può anche considerare la funzione erf(x) (funzione errore) così definita:
erf( x ) = 1 − erfc( x ) =
2
π
∞
( )
2
∫ exp − y dy −
0
2
π
∞
( )
2
∫ exp − y dy =
x
2
π
x
∫ exp ( − y
2
)dy
(52)
0
Utilizzando le funzioni erfc(x) ed erf(x), la distribuzione di probabilità cumulativa della variabile
aleatoria gaussiana può scriversi come:
FX ( x) =
1
π
x−μ
2σ
∫
−∞
( )
exp − y dy =
2
1
π
+∞
∫ exp ( − y
−∞
2
)dy −
1
π
+∞
∫
x−μ
2σ
( )
exp − y 2 dy =
(53)
1
1⎡
⎛x−μ⎞
⎛ x − μ ⎞⎤ 1 ⎡
⎛ x − μ ⎞⎤
= 1 − erfc ⎜
= 1 − ⎢1 − erf ⎜
= ⎢1 + erf ⎜
⎥
⎟
⎟
⎟⎥
2
2⎣
⎝ 2σ ⎠
⎝ 2σ ⎠ ⎦ 2 ⎣
⎝ 2σ ⎠ ⎦
Considerato che dalla conoscenza di fX(x) o di FX(x) è possibile ricavare la probabilità di qualunque
evento legato alla variabile aleatoria X, se ne conclude che, dal punto di vista computazionale, ciò
che serve è il valore della funzione erfc(x) (o, il che è lo stesso, della funzione erf(x)). Come
anticipato più sopra, tali funzioni sono normalmente disponibili nei più diffusi software di calcolo o
almeno riportate in opportune tabelle con un prefissato passo di discretizzazione. Esempi di tali
tabelle sono allegati alla dispensa, per valori di x compresi tra 0 e (circa) 6, normalmente sufficienti
per le applicazioni. E’ anche interessante osservare che i valori di tali funzioni relative ad argomenti
negativi si ottengono facilmente dai valori delle funzioni con argomenti positivi. Utilizzando le
definizioni, si ha infatti:
15
2
erfc( − x) =
π
2
=
π
∞
∫
( )
−x
x
∫ exp ( − y
2
0
2
exp − y 2 dy =
π
∫
−x
( )
exp − y 2 dy +
2
π
∞
∫ exp ( − y
2
)dy
0
)dy + 1 = 1 + erf ( x)
(54)
0
mentre:
−x
2
erf (− x ) =
π
∫ exp ( − y
2
)dy = −
0
2
π
x
∫ exp ( − y
2
)dy = −erf ( x)
(55)
0
Dalla (55), in particolare, si evince che la funzione erf(x) è una funzione dispari.
Talora, invece della funzione erfc(x) si considera la funzione Q(x) così definita:
1
Q( x) =
2π
∞
⎛ y2 ⎞
exp
∫ ⎜⎜ − 2 ⎟⎟dy
⎝
⎠
x
(56)
Con un semplice cambiamento di variabile ( t = y / 2 ) è immediato determinare il legame tra le
due funzioni:
Q( x) =
1
⎛ x ⎞
erfc ⎜
⎟
2
⎝ 2⎠
(57)
Rayleigh
Si tratta di una variabile aleatoria continua caratterizzata dalla densità di probabilità:
⎧ x
⎛ x2 ⎞
exp
⎪⎪ 2
⎜⎜ − 2 ⎟⎟
f X ( x) = ⎨ σ
⎝ 2σ ⎠
⎪
0
⎪⎩
x≥0
(58)
x<0
(il significato del parametro σ risulterà chiaro successivamente).
Per integrazione si ottiene:
⎧⎡
⎛ x2 ⎞⎤
⎪⎪ ⎢1 − exp ⎜ − 2 ⎟ ⎥
⎜ 2σ ⎟ ⎥
FX ( x) = ⎨ ⎢⎣
⎝
⎠⎦
⎪
0
⎪⎩
x≥0
(59)
x<0
Binomiale
Si tratta di una variabile aleatoria discreta, associata all’esperimento di Bernoulli descritto in
precedenza, e caratterizzata dalla densità di probabilità:
f X ( x) =
n
⎛n⎞
∑ ⎜ k ⎟ p k (1 − p)n−k δ ( x − k )
k =0 ⎝
(60)
⎠
16
dove X = k comporta che, in n prove ripetute, per k volte si è avuto l’esito che ha probabilità p di
verificarsi.
Trattandosi di variabile aleatoria discreta, la distribuzione di probabilità cumulativa è una funzione
costante a tratti, il cui andamento, alla stregua di quello di fX(x), dipende fortemente da p. A mo’ di
esempio, per p = 1/2 la (60) fornisce:
f X ( x) =
n
⎛n⎞ 1
∑ ⎜ k ⎟ 2n δ ( x − k )
k =0 ⎝
(61)
⎠
e utilizzando la (33) si ricava:
1
n
⎛n⎞
∑ ⎜ k ⎟ u( x − k )
2n
FX ( x) =
k =0 ⎝
(62)
⎠
Tenendo conto dell’andamento del coefficiente binomiale, l’entità dei gradini è massima
nell’intorno di x = n/2; Per il resto, si tratta di una funzione costantemente uguale a 0 per x < 0 e
costantemente uguale a 1 per x > n.
Poisson
Si tratta di una variabile aleatoria discreta caratterizzata dalla densità di probabilità:
f X ( x) =
∞
λk
k =0
k!
∑
exp(−λ )δ ( x − k )
(63)
(il significato del parametro λ risulterà chiaro successivamente).
Per integrazione, ovvero utilizzando direttamente la (33), in questo caso si trova:
∞
λk
k =0
k!
FX ( x) = exp(−λ ) ∑
u( x − k )
(64)
*****
Indicatori statistici
La conoscenza della funzione densità di probabilità (o, il che è lo stesso, della distribuzione di
probabilità cumulativa) fornisce una descrizione completa del comportamento di una variabile
aleatoria. In molti casi, comunque, una conoscenza così dettagliata non è necessaria e ci si può
accontentare della determinazione di alcuni parametri caratteristici, i più importanti dei quali sono
riassunti di seguito.
Valore medio
Per una variabile aleatoria X con densità di probabilità fX(x) il valore medio è fornito dal seguente
integrale:
+∞
mX =
∫ xf X ( x)dx
(65)
−∞
17
Il valore medio ha, essenzialmente, il significato di “baricentro” attorno al quale si distribuiscono i
valori della variabile aleatoria.
Nel caso particolare di variabile aleatoria discreta, la precedente può riscriversi:
+∞
mX =
∫ xf X ( x)dx =
−∞
+∞
∫
−∞
x ∑ p k δ ( x − x k )dx = ∑ p k
k
k
+∞
∫ xδ ( x − xk )dx = ∑ pk xk
−∞
(66)
k
Avendo sfruttato, nell’ultimo passaggio la proprietà di campionamento della delta di Dirac. Inoltre,
nella (66) si è posto, per semplificare la notazione, Pr{X = xk} = pk.
E’ interessante osservare che la precedente può essere utilizzata per calcolare il valore medio anche
di una generica funzione Y = g(X) della variabile aleatoria X, in accordo con l’espressione seguente:
+∞
mY =
∫ g ( x) f X ( x)dx
(67)
−∞
Più esplicitamente, nel seguito di questa dispensa si mostrerà come sia possibile, in condizioni non
particolarmente restrittive, calcolare la funzione densità di probabilità fY(y) a partire dalla
conoscenza della fX(x) oltre che, ovviamente, del legame funzionale tra X e Y. Una volta nota fY(y),
mY si può chiaramente calcolare come:
+∞
mY =
∫ yfY ( y)dy
(68)
−∞
Nondimeno, ciò che le considerazioni precedenti mettono in evidenza è che ai fini del calcolo del
valore medio la conoscenza di fY(y) non è strettamente necessaria, potendosi utilizzare direttamente
la (67).
Il valore medio di una variabile viene spesso indicato con la lettera E, iniziale del termine inglese
Expectation. Si ha dunque, ad esempio:
E { X } = mX
(69)
Come ulteriore alternativa si ha anche la seguente, non meno classica, notazione:
X = E { X } = mX
(70)
Nel seguito questi simboli verranno utilizzati, in maniera “interscambiabile”, come equivalenti.
Valore quadratico medio
Si tratta di una particolare applicazione della (67) in cui Y = g(X) = X2.
Di conseguenza, per una variabile aleatoria X con densità di probabilità fX(x), il valore quadratico
medio è definito dal seguente integrale:
+∞
X
2
=
∫x
2
f X ( x)dx
(71)
−∞
Nel caso particolare di variabile aleatoria discreta, la precedente può riscriversi:
18
+∞
X
2
=
∫x
+∞
2
f X ( x)dx =
−∞
∫
+∞
x
2
−∞
∑ pk δ ( x − xk )dx = ∑ pk ∫ x 2δ ( x − xk )dx = ∑ pk xk2
k
−∞
k
(72)
k
Varianza
Per una variabile aleatoria X con densità di probabilità fX(x) la varianza è fornita dal seguente
integrale:
+∞
σ X2
= ( X − mX )
2
x − m X ) f X ( x)dx
(
∫
=
2
(73)
−∞
La varianza misura il livello di dispersione della variabile aleatoria intorno al valore medio. La sua
radice quadrata σ prende il nome di deviazione standard (o scarto quadratico medio).
Molto importante è il legame che esiste tra la varianza, il valore quadratico medio e il valore medio.
Questo legame può essere ricavato facilmente dalla definizione precedente. Si ha infatti:
σ X2 =
+∞
2
∫ ( x − mX ) f X ( x)dx =
−∞
= X
2
− 2m + m = X
2
X
2
X
+∞
∫
+∞
x 2 f X ( x)dx − 2mX
−∞
2
∫
+∞
xf X ( x)dx + mX2
−∞
−m
∫
f X ( x)dx
−∞
(74)
2
X
avendo sfruttato, nell’ultimo termine, anche la proprietà di normalizzazione.
Momenti e momenti centrali
Benché la conoscenza del valore medio, del valore quadratico medio e della varianza fornisca
tipicamente informazioni adeguate sulla variabile aleatoria (ove non si conosca o non si voglia
considerare per intero la funzione densità di probabilità) la descrizione della variabile può essere
ulteriormente perfezionata estendendo le definizioni precedenti.
Data una variabile aleatoria X con densità di probabilità fX(x), si definisce momento di ordine j di
tale variabile il seguente integrale:
+∞
Mj = X j =
∫x
j
f X ( x)dx
j = 1, 2, 3, …
(75)
−∞
E’ chiaro che per j = 1 la precedente restituisce il valore medio, che ha dunque il significato di
momento di ordine 1; analogamente, per j = 2 la precedente restituisce il valore quadratico medio,
che ha dunque il significato di momento di ordine 2.
Per la stessa variabile aleatoria X si definisce invece momento centrale di ordine j il seguente
integrale:
σ j = ( X − mX ) j =
+∞
j
∫ ( x − mX ) f X ( x)dx =
−∞
+∞
∫ (x − M )
1
j
f X ( x)dx
−∞
Per j = 2 si riottiene la varianza; si ha dunque: σ2 = σX2.
Sviluppando la potenza j-esima entro integrale, peraltro, si ottiene:
19
j = 2, 3, …
(76)
j
⎛ j⎞
k =0
⎝ ⎠
σ j = ∑ ⎜ ⎟ (− M 1 )k M j −k
k
j = 2, 3, …
(77)
espressione quest’ultima che lega i momenti centrali σj ai momenti Mj della variabile aleatoria X.
Nella (77) si deve porre M0 = 1, come del resto è giustificato dalla definizione (75) la quale per j = 0
restituisce la condizione di normalizzazione.
I momenti di una variabile aleatoria, ancorché con le espressioni integrali sopra riportate, possono
essere ricavati anche utilizzando la cosiddetta funzione caratteristica, così definita:
+∞
C X (u ) = exp(iux) =
∫ exp(iux) f
X
( x)dx
(78)
−∞
Nella (77), u è una variabile “formale” (non ha cioè un significato specifico in relazione alla
variabile aleatoria X). Nondimeno, confrontando la (78) con la definizione di antitrasformata di
Fourier, sostituendo in quella definizione t con u e ω con x, è facile concludere che CX(u) può essere
appunto interpretata come l’antitrasformata di fX(x), moltiplicata per 2π. Vale allora, ovviamente,
anche la relazione inversa, in virtù della quale la densità di probabilità della variabile aleatoria X
può essere ottenuta dalla trasformata di Fourier della sua funzione caratteristica, divisa per 2π; si ha
cioè:
+∞
f X ( x) =
1
∫ exp(−iux)CX (u )du
2π −∞
(79)
Densità di probabilità e funzione caratteristica della variabile aleatoria X costituiscono quindi una
coppia trasformata-antitrasformata e la conoscenza dell’una è completamente equivalente alla
conoscenza dell’altra.
Ciò che interessa ora mettere in evidenza è che, proprio in ragione di questo legame, la funzione
caratteristica può essere utilizzata per ricavare i momenti della variabile aleatoria. Vale infatti la
seguente relazione:
M j = (−i ) j
d j C (u )
du j u =0
j = 1, 2, ….
(80)
La verifica di questa proprietà è immediata. Utilizzando la (78) si ha infatti:
j
d j C (u )
j d
(−i )
(
i
)
=
−
du j u = 0
du j
j
+∞
∫ exp(iux) f X ( x)dx
−∞
+∞
= (−i )
u =0
+∞
= (−i ) j (i ) j
∫x
j
dj
∫ du j exp(iux) f X ( x)dx =
−∞
u =0
+∞
j
=
exp(iux) f X ( x)dx
−∞
u =0
∫x
j
(81)
f X ( x)dx = M j
−∞
Per una variabile aleatoria discreta la funzione caratteristica, utilizzando la (34) ove si ponga, per
semplicità, Pr{X = xk} = pk, diventa:
C X (u ) = ∑ pk exp(iuxk )
(82)
k
20
Con semplici calcoli, è possibile ricavare la funzione caratteristica per alcuni degli esempi di
variabile aleatoria forniti più sopra. I relativi andamenti sono riportati in Tabella I.
Variabile aleatoria
Funzione caratteristica
1 exp(iub) − exp(iua)
b−a
iu
a
a − iu
a2
a2 + u2
⎛ u 2σ 2 ⎞
exp(iu μ ) exp ⎜ −
⎟
2 ⎠
⎝
Uniforme
Esponenziale unilatera
Esponenziale bilatera
Gaussiana
[1 − p + p exp(iu )]
exp {λ [ exp(iu ) − 1]}
n
Binomiale
Poisson
Tabella I
Questi andamenti possono essere utilizzati per ricavare, in particolare, valor medio, valore
quadratico medio e varianza della variabile aleatoria in esame. Questi calcoli sono lasciati, per
esercizio, al lettore.
*****
Funzioni di variabile aleatoria
In molti problemi di interesse pratico, nota che sia la descrizione statistica di una variabile aleatoria
X, per esempio tramite la conoscenza della densità di probabilità fX(x) si è interessati a risalire alla
descrizione statistica di una variabile aleatoria Y legata a X dalla relazione
Y = g( X )
(83)
Se g(X) è una funzione monotona, crescente o decrescente, il problema può essere immediatamente
risolto; si verifica infatti che risulta:
fY ( y ) =
f X ( x)
g '( x)
(84)
−1
x= g ( y )
dove si è posto g’(x) = dg(x)/dx, e si è indicata con g−1(Y) la funzione inversa della (83) (che esiste
sicuramente perché la funzione è monotona).
Esempio
Sia X una variabile aleatoria gaussiana, con densità di probabilità:
f X ( x) =
1
2πσ X
⎡ ( x − μ X )2 ⎤
exp ⎢ −
⎥
2σ X2 ⎥⎦
⎢⎣
Sia inoltre
21
Y = aX + b
Questa funzione, per qualunque valore di a e b è certamente monotona. Si può quindi applicare la
(84), dove la funzione inversa sarà:
X=
Y −b
a
D’altro canto:
g '( x) = a
Sostituendo si ottiene allora:
fY ( y ) =
1
a
1
2π σ X
2
⎡ ⎛ y −b
⎞ ⎤
− μX ⎟ ⎥
⎢ ⎜
⎡ ( y − b − aμ )2 ⎤
1
a
X
⎝
⎠
⎢
⎥
⎥
exp −
exp ⎢ −
=
2
2 2
⎢
⎥
2π a σ X
2σ X
2a σ X
⎢⎣
⎥⎦
⎢
⎥
⎥⎦
⎣⎢
Si tratta ancora di una variabile aleatoria gaussiana, ma con valore medio:
μY = aμ X + b
e varianza:
σ Y2 = a 2σ X2
ovvero deviazione standard:
σY = a σ X
*****
Nel caso in cui la funzione (83) non sia monotona ma l’intervallo di variabilità della X sia
decomponibile in un numero finito di regioni in cui la funzione è monotona, la densità di probabilità
della variabile aleatoria Y può essere ricavata come:
fY ( y ) = ∑
i
f X ( xi )
g '( xi )
(85)
−1
xi = g ( y )
dove l’insieme {xi} è costituito da tutte le soluzioni dell’equazione (83). Esplicitamente ciò equivale
a dire che:
− si individuano i sottointervalli della variabile aleatoria X in cui la (83) è monotona
− si determinano i corrispondenti intervalli della variabile aleatoria Y
− entro ciascun sottointervallo si applica la (84), che fornirà l’andamento “locale” della
densità di probabilità cercata
22
− si sovrappongono i risultati parziali così ottenuti
Esempio
Sia X una variabile aleatoria gaussiana, con densità di probabilità:
f X ( x) =
1
2πσ X
⎡ ( x − μ X )2 ⎤
exp ⎢ −
⎥
2σ X2 ⎥⎦
⎢⎣
Sia inoltre
Y= X
Questa funzione è monotona per X ≥ 0, dove si ha:
X =Y
e per X ≤ 0, dove si ha:
X = −Y
Il range di variabilità di X può dunque essere diviso in due sottointervalli, e si hanno due contributi
nella (85). È opportuno, come spiegato più sopra, calcolare questi contributi separatamente.
Valori di X ≥ 0 vengono “trasformati” dalla funzione assegnata in valori di Y ≥ 0.
Il relativo contributo alla densità di probabilità vale:
fY ( y ) =
1
2πσ X
⎡ ( y − μ X )2 ⎤
exp ⎢ −
⎥
2σ X2 ⎥⎦
⎢⎣
in quanto in questo caso non vengono cambiati né il valore medio e né la varianza.
Valori di X ≤ 0 vengono anch’essi “trasformati” dalla funzione assegnata in valori di Y ≥ 0.
Il relativo contributo alla densità di probabilità vale:
fY ( y ) =
1
2πσ X
⎡ (− y − μ X )2 ⎤
⎡ ( y + μ X )2 ⎤
1
exp ⎢ −
exp
=
⎥
⎢−
⎥
2πσ X
2σ X2
2σ X2 ⎥⎦
⎢⎣
⎥⎦
⎢⎣
Come detto, ambedue questi contributi devono essere riferiti a valori di Y ≥ 0 per cui, in definitiva,
si ha:
⎧ 1
⎡ ( y − μ X )2 ⎤
⎡ ( y + μ X )2 ⎤
1
−
+
exp
exp
⎪⎪
⎢
⎥
⎢−
⎥
2π σ X
2σ X2 ⎥⎦
2σ X2 ⎥⎦
⎢⎣
⎢⎣
fY ( y ) = ⎨ 2π σ X
⎪
0
⎪⎩
y≥0
y<0
Valori di Y < 0, infatti, non sono possibili. Come si vede (e come prevedibile) la variabile Y non è
più una variabile gaussiana.
23
*****
Un caso che deve essere trattato separatamente riguarda la possibilità che la funzione (83) sia
costante in uno (o più) degli intervalli di variabilità. Ciò corrisponde al fatto che un insieme di
valori di X produce lo stesso valore di Y.
Sulla base del significato stesso di probabilità, è qualitativamente ragionevole che la probabilità che
X assuma valori all’interno dell’intervallo in cui la (83) è costante si trasferisca alla probabilità che
Y assuma il valore costante. Il risultato della trasformazione è dunque una variabile aleatoria mista,
in cui alcuni valori di Y hanno probabilità diversa da zero di verificarsi (mentre si è visto in
precedenza che nel caso di variabile aleatoria continua la probabilità di un valore isolato è
identicamente nulla).
Esempio
Sia X una variabile aleatoria gaussiana, con densità di probabilità:
f X ( x) =
1
2πσ X
⎡ ( x − μ X )2 ⎤
exp ⎢ −
⎥
2σ X2 ⎥⎦
⎢⎣
Sia inoltre
⎧X
Y =⎨
⎩0
X ≥0
X <0
Questa funzione è monotona per X ≥ 0, dove si ha:
X =Y
Tutti i valori di X < 0, invece, vengono trasformati nel valore Y = 0. Questo significa che la Pr{Y =
0} sarà uguale alla Pr{X < 0}. In formule:
Pr {Y = 0} =
0
∫
−∞
1
f X ( x)dx =
2πσ X
1
=
πμ
+∞
∫
X
/( 2σ X )
− μ X /( 2σ X )
⎡ ( x − μ X )2 ⎤
1
2
∫ exp ⎢⎢ − 2σ 2 ⎥⎥dx = π ∫ exp − y dy =
X
⎣
⎦
−∞
−∞
0
( )
exp − y 2 dy =
( )
⎛ μX
1
erfc ⎜⎜
2
⎝ 2σ X
⎞
⎟⎟
⎠
Si noterà che, in virtù della seconda delle (51), quando μX = 0 questa probabilità vale 1/2.
D’altro canto, nel tratto in cui la funzione è monotona, e che corrisponde a valori di Y ≥ 0, si applica
la (84) la quale fornisce:
fY ( y ) =
1
2πσ X
⎡ ( y − μ X )2 ⎤
exp ⎢ −
⎥
2σ X2 ⎥⎦
⎢⎣
In definitiva si può scrivere, combinando i risultati:
24
fY ( y ) =
1
2π σ X
⎡ ( y − μ X )2 ⎤
⎛ μX ⎞
1
exp ⎢ −
⎥ u ( y ) + erfc ⎜
⎟δ ( y)
2
2
2σ X ⎦⎥
⎝ 2σ X ⎠
⎣⎢
avendo indicato con u(y) la funzione gradino unitario che parte dall’origine.
*****
Coppie di variabili aleatorie
Consideriamo una coppia di variabili aleatorie X e Y. Singolarmente, esse saranno caratterizzate
dalle rispettive densità di probabilità fX(x) e fY(y) o, il che è lo stesso dalle rispettive distribuzioni di
probabilità cumulativa FX(x) e FY(y). Ciò che però può essere di interesse è la descrizione statistica
congiunta di queste variabili, ad esempio la probabilità che X sia minore o uguale di un valore
prefissato x e, contemporaneamente, Y sia minore o uguale di un valore prefissato y. Proprio a
partire da questo esempio, si definisce distribuzione di probabilità congiunta delle due variabili la
seguente funzione:
FXY ( x, y ) = Pr { X ≤ x, Y ≤ y}
(86)
La valutazione della distribuzione di probabilità congiunta risulta particolarmente semplice nel caso
in cui le variabili X e Y sono tra loro statisticamente indipendenti. Ricordando infatti la definizione
di statistica indipendenza già fornita in precedenza e, in particolare, la relazione (14) è immediato
concludere che, in questo caso, si ha:
FXY ( x, y ) = Pr { X ≤ x} ⋅ Pr {Y ≤ y} = FX ( x) ⋅ FY ( y )
(87)
Nel caso più generale, è però evidente che la (87) non può essere vera se, come si verifica in molti
esperimenti aleatori, le variabili X e Y si influenzano reciprocamente. Peraltro, è qualitativamente
del tutto ragionevole che la funzione FXY(x,y) determini le proprietà statistiche marginali, cioè
relative alle singole variabili della coppia.
Valgono le seguenti proprietà:
G.1 – FXY(x,y) assume valori appartenenti all’intervallo [0, 1], cioè:
0 ≤ FXY ( x, y ) ≤ 1
(88)
G.2 – FXY(x,y0), comunque si scelga il valore y0 della variabile Y, è monotona non decrescente nella
variabile X e continua da destra in questa variabile; analogamente, FXY(x0,y), comunque si scelga il
valore x0 della variabile X, è monotona non decrescente nella variabile Y e continua da destra in
questa variabile.
G.3 – FXY(x,y) soddisfa le seguenti uguaglianze:
FXY (−∞, y ) = Pr { X ≤ −∞, Y ≤ y} = 0
(89a)
FXY ( x, −∞ ) = Pr { X ≤ x, Y ≤ −∞} = 0
(89b)
FXY ( −∞, −∞) = Pr { X ≤ −∞, Y ≤ −∞} = 0
(89c)
25
G.4 – le distribuzioni di probabilità cumulative delle variabili X e Y (distribuzioni marginali) si
ottengono come segue:
FX ( x) = FXY ( x, +∞)
(90a)
FY ( y) = FXY (+∞, y )
(90b)
G.5 – il limite di FXY(x,y) quando sia x che y tendono a +∞ è unitario, si ha cioè:
FXY (+∞, +∞) = 1
(91)
G.6 – la probabilità dell’evento “rettangolare”: {x1 < X ≤ x2, y1 < Y ≤ y2} può essere calcolato
mediante la relazione seguente:
Pr { x1 < X ≤ x2 , y1 < Y ≤ y2 } = FXY ( x2 , y2 ) − FXY ( x1 , y2 ) − FXY ( x2 , y1 ) + FXY ( x1 , y1 )
(92)
Gran parte di queste proprietà sono analoghe (e possono essere interpretate come la logica
estensione) di quelle enunciate in precedenza per le distribuzioni delle singole variabili. Le (90), in
particolare, si giustificano sulla base del fatto che, per ottenere le distribuzioni marginali di una
variabile occorre “saturare” l’altra variabile.
Quanto detto sin qui per le distribuzioni di probabilità cumulativa può ovviamente essere esteso alle
densità di probabilità. Definiamo allora la seguente densità di probabilità congiunta:
f XY ( x, y ) =
∂ 2 FXY ( x, y )
∂x∂y
(93)
La relazione inversa della (93) consente invece di calcolare la distribuzione di probabilità congiunta
a partire dalla densità di probabilità, come segue:
x
FXY ( x, y ) =
y
∫ ∫
f XY (α , β )dα d β
(94)
α =−∞ β =−∞
Nel caso di variabili statisticamente indipendenti si ha:
f XY ( x, y ) = f X ( x) fY ( y )
(95)
Alla stregua della distribuzione di probabilità cumulativa, anche la densità di probabilità congiunta
gode di una serie di proprietà; le più importanti sono elencate di seguito:
H.1 – fXY(x,y) assume valori non negativi, cioè:
f XY ( x, y ) ≥ 0
(96)
H.2 – l’integrale di fXY(x,y) sull’intero piano x-y vale 1 (proprietà di normalizzazione), cioè:
26
+∞
∫
+∞
∫
f XY ( x, y )dxdy = 1
(97)
x =−∞ y =−∞
H.3 – le densità di probabilità marginali delle variabili X e Y si ottengono come segue:
+∞
f X ( x) =
∫
f XY ( x, y )dy
(98a)
f XY ( x, y )dx
(98b)
−∞
+∞
fY ( y ) =
∫
−∞
H.4 – la probabilità di un evento A = {( X , Y ) ∈ D} individuato da un dominio D nel piano x-y è data
da:
Pr( A) = ∫∫ f XY ( x, y )dxdy
(99)
D
*****
Già in precedenza si è avuto modo di introdurre il concetto di probabilità condizionata. Date due
variabili aleatorie X e Y, per estensione della (9) si può introdurre la densità di probabilità
condizionata della variabile aleatoria Y, rispetto all’evento {X = x}:
fY | X ( y | x) =
f XY ( x, y )
f X ( x)
(100)
D’altro canto, per definizione:
fY | X ( y | x) =
dFY | X ( y | x)
(101)
dy
e quindi la distribuzione di probabilità condizionata della variabile aleatoria Y, rispetto all’evento
{X = x} risulta:
y
y
FY | X ( y | x) =
∫
y
fY | X ( β | x ) d β =
β =−∞
∫
β =−∞
f XY ( x, β )
dβ =
f X ( x)
∫
f XY ( x, β )d β
β =−∞
f X ( x)
(102)
Scambiando i ruoli di X e Y, relazioni analoghe si trovano per la densità di probabilità condizionata
della variabile aleatoria X, rispetto all’evento {Y = y}:
f X |Y ( x | y ) =
f XY ( x, y )
fY ( y )
(103)
27
e per la distribuzione di probabilità condizionata della variabile aleatoria X, rispetto all’evento {Y =
y}:
x
x
∫
FX |Y ( x | y ) =
x
f X |Y (α | y )dα =
α =−∞
∫
α =−∞
∫ f XY (α , y)dα
f XY (α , y )
dα = α =−∞
fY ( y )
fY ( y )
(104)
dove, per definizione, si ha qui:
f X |Y ( x | y ) =
dFX |Y ( x | y )
(105)
dx
Nel caso di variabili aleatorie X e Y statisticamente indipendenti, in virtù della (95), le (100) e (103)
forniscono, rispettivamente:
f Y | X ( y | x ) = fY ( y )
(106)
f X |Y ( x | y ) = f X ( x )
(107)
e
come è giusto che sia, in considerazione della definizione stessa di statistica indipendenza.
Nel caso più generale, invece, dal confronto tra le (100) e (103) si ricava:
f X |Y ( x | y ) fY ( y ) = fY | X ( y | x ) f X ( x )
(108)
che a sua volta richiama la formula di Bayes (15).
*****
Momenti congiunti e momenti centrali congiunti
Utilizzando le funzioni FXY(x,y) e fXY(x,y), le definizioni di momenti e momenti centrali fornite in
precedenza per una variabile aleatoria possono essere estese a coppie di variabili aleatorie.
Si definisce allora momento congiunto di ordine (j,k) della coppia di variabili aleatorie X, Y il
seguente integrale:
+∞
M jk = X Y
j
k
=
+∞
∫ ∫
x j y k f XY ( x, y )dxdy
j, k = 0, 1, 2, 3, …
(109)
x =−∞ y =−∞
Particolarmente importante è il momento congiunto di ordine (1,1) il quale, utilizzando la (109),
risulta:
+∞
M 11 = XY =
+∞
∫ ∫
xyf XY ( x, y )dxdy
(110)
x =−∞ y =−∞
Il momento congiunto di ordine (1,1) prende il nome di correlazione. Nel caso di variabili
statisticamente indipendenti, è immediato verificare che esso è dato dal prodotto dei momenti di
28
ordine 1 delle variabili singole (ovvero, esplicitamente, dal prodotto dei valori medi). Si ha infatti,
in questo caso:
+∞
M 11 =
+∞
∫ ∫
+∞
∫ xf
xyf X ( x) fY ( y )dxdy =
x =−∞ y =−∞
−∞
+∞
X
( x)dx ∫ yfY ( y )dy = mX mY
(111)
−∞
Quando è verificata la (111), si dice che le variabili X e Y sono tra loro incorrelate. Se dunque è
certamente vero che la statistica indipendenza implica l’incorrelazione non è ovviamente vero, in
generale 5 , l’inverso, in quanto la correlazione può essere numericamente uguale al prodotto dei
valori medi anche quando le variabili non sono statisticamente indipendenti.
Un caso particolare si verifica quando le variabili sono incorrelate e una almeno di esse ha valor
medio nullo; nel qual caso la (111) fornisce:
M 11 = mX mY = 0
(112)
Per estensione della terminologia introdotta nella teoria dei segnali determinati, si dice che le
variabili X e Y che verificano la condizione M11 = 0 sono tra loro ortogonali. Peraltro, si faccia
attenzione al fatto che la condizione di ortogonalità può essere verificata anche se le variabili non
sono incorrelate (ovvero, a maggior ragione, statisticamente indipendenti).
Incidentalmente, può anche essere interessante osservare che, dalla definizione (109), risulta:
M 10 = X = m X
(113a)
M 01 = Y = mY
(113b)
Si definisce invece momento centrale congiunto di ordine (j,k) il seguente integrale:
+∞
σ jk = ( X − mX ) j (Y − mY ) k =
+∞
∫ ∫
( x − mX ) j ( y − mY ) k f XY ( x, y )dxdy
j, k = 1, 2, … (114)
x =−∞ y =−∞
Anche qui riveste particolare importanza il caso j = k = 1. Il momento congiunto che ne risulta:
σ 11 = ( X − mX )(Y − mY ) =
+∞
+∞
∫ ∫
( x − mX )( y − mY ) f XY ( x, y )dxdy
x =−∞ y =−∞
prende il nome di covarianza.
La covarianza può essere espressa in funzione dei momenti definiti più sopra.
Si ha infatti:
5
Una importante eccezione verrà discussa nel seguito di questa dispensa.
29
(115)
+∞
σ 11 =
+∞
+∞
∫ ∫
+∞
+∞
+∞
yf XY ( x, y )dxdy − mY
x =−∞ y =−∞
+∞
+ mX mY
xyf XY ( x, y )dxdy +
x =−∞ y =−∞
∫ ∫
− mX
∫ ∫
( x − mX )( y − mY ) f XY ( x, y )dxdy =
x =−∞ y =−∞
+∞
+∞
∫ ∫
xf XY ( x, y )dxdy +
(116)
x =−∞ y =−∞
+∞
∫ ∫
f XY ( x, y )dxdy = M 11 − mX mY − mX mY + mX mY = M 11 − mX mY
x =−∞ y =−∞
Se poi le variabili sono incorrelate (e lo sono certamente quando sono statisticamente indipendenti)
è chiaro che risulta:
σ 11 = 0
(117)
Proprio in virtù di questo risultato, si conviene di assumere σ11 come misura della correlazione
statistica di due variabili aleatorie. In realtà tale parametro viene normalizzato, in modo da
assumere valori, in modulo, non maggiori dell’unità. Questo obiettivo si consegue dividendo per la
deviazione standard delle variabili X e Y. Il risultato di tale rapporto:
ρ XY =
σ 11
σ 11
=
σ XσY
σ X2 σ Y2
(118)
prende il nome di coefficiente di correlazione.
Il fatto che il coefficiente di correlazione fornito dalla (118) assuma valori, in modulo, compresi tra
0 e 1 è conseguenza del fatto, qualitativamente ragionevole, che se da una parte si ha incorrelazione
quando σ11 = 0, la massima correlazione corrisponde ad un legame di lineare dipendenza tra X e Y:
Y = aX + b
(119)
Valendo la (119), risulta:
mY = amX + b
(120a)
⎡ +∞
⎤
M 11 = ∫ ∫ x(ax + b) f XY ( x, y )dxdy = a ∫ x ⎢ ∫ f XY ( x, y )dy ⎥dx +
x =−∞ y =−∞
x =−∞
⎣⎢ y =−∞
⎦⎥
+∞
+∞
+∞
2
+∞
+∞
⎡ +∞
⎤
+ b ∫ x ⎢ ∫ f XY ( x, y )dy ⎥dx = a ∫ x 2 f X ( x)dx + b ∫ xf X ( x)dx = a X 2 + bmX
⎢ y =−∞
x =−∞ ⎣
−∞
−∞
⎦⎥
+∞
(120b)
e quindi, in virtù della (116):
(
)
σ 11 = a X 2 + bmX − amX2 − bmX = a X 2 − mX2 = aσ X2
(121)
D’altro canto è anche:
σ Y2 = a 2σ X2
(122)
30
e quindi:
ρ XY =
a
a
(123)
La (123) comporta:
ρ XY = 1
per a > 0
ρ XY = −1
(124a)
per a < 0
(124b)
Quando sono legate dalla relazione (119) che comporta, come si è verificato, ρ XY = 1 , si dice che X
e Y sono tra loro completamente correlate.
La funzione caratteristica ha ovviamente significato anche per una coppia di variabili aleatorie. In
particolare, si definisce funzione caratteristica congiunta delle variabili X e Y la seguente funzione
delle variabili formali u e v:
C XY (u, v) = exp [i (ux + vy ) ] =
+∞
+∞
∫ ∫
exp [i (ux + vy ) ] f XY ( x, y )dxdy
(125)
x =−∞ y =−∞
CXY(u,v) può essere interpretata come un’antitrasformata di Fourier bidimensionale moltiplicata per
4π2. La funzione che viene antitrasformata è la densità di probabilità congiunta fXY(x,y); u, x e v, y
sono coppie di variabili coniugate. La trasformazione inversa restituisce allora la densità di
probabilità congiunta a partire dalla funzione caratteristica congiunta; si ha cioè:
1
f XY ( x, y ) = 2
4π
+∞
+∞
∫ ∫
C XY (u, v) exp [ −i (ux + vy ) ] dudv
(126)
u =−∞ v =−∞
Come già nel caso di variabili singole, anche per una coppia di variabili aleatorie la funzione
caratteristica ha il significato di funzione generatrice di momenti (in questo caso, momenti
congiunti). Si dimostra infatti il seguente risultato:
M jk = (−i ) j + k
∂ j ∂ k C XY (u, v)
∂u j ∂v k
u =0
j, k = 1, 2, ….
(127)
v=0
Un’altra proprietà molto importante è la seguente: se le variabili X e Y sono statisticamente
indipendenti allora la funzione caratteristica congiunta è pari al prodotto delle funzioni
caratteristiche delle singole variabili; in formula:
C XY (u, v) = C X (u )CY (v)
(128)
La verifica di questa proprietà è immediata, discendendo direttamente dalla definizione.
Se infatti si introduce la (95) nella (125) si ottiene:
31
+∞
+∞
∫ ∫
C XY (u, v) =
exp [i (ux + vy ) ] f X ( x) fY ( y )dxdy =
x =−∞ y =−∞
+∞
∫ exp(iux) f
−∞
+∞
X
( x)dx ⋅
(129)
⋅ ∫ exp(ivy ) fY ( y )dy = C X (u )CY (v)
−∞
Tutte le definizioni fornite possono ovviamente essere particolarizzate al caso di una coppia di
variabili aleatorie discrete. Le espressioni relative sono qui omesse per brevità.
*****
Variabili aleatorie gaussiane miste
Si è osservato in precedenza che la statistica indipendenza è condizione più restrittiva
dell’incorrelazione. Esplicitamente questo significa che due variabili aleatorie statisticamente
indipendenti sono sicuramente incorrelate, ma due variabili aleatorie incorrelate possono non essere
statisticamente indipendenti.
Consideriamo ora una coppia di variabili aleatorie X e Y descritte da una densità di probabilità
congiunta del tipo seguente:
f XY ( x, y ) =
1
2πσ X σ Y
⎧⎪
⎡ ( x − mX ) 2 ( y − mY ) 2
1
( x − mX )( y − mY ) ⎤ ⎫⎪
+
− 2ρ
exp ⎨−
⎢
⎥⎬
2
2
2
σY
σ XσY
1− ρ 2
⎦ ⎭⎪
⎩⎪ 2(1 − ρ ) ⎣ σ X
(130)
dove ρ è un opportuno parametro.
Le densità di probabilità marginali delle variabili X e Y possono essere ricavate applicando le (98).
Per integrazione, è facile verificare che si ottiene:
f X ( x) =
⎡ ( x − mX ) 2 ⎤
1
exp ⎢ −
⎥
2σ X2 ⎦
2πσ X
⎣
(131a)
fY ( y ) =
⎡ ( y − mY ) 2 ⎤
1
exp ⎢ −
2σ Y2 ⎥⎦
2πσ Y
⎣
(131b)
X e Y, quindi, sono due variabili separatamente gaussiane, con valori medi mX e mY, e varianze σX2 e
σY2, rispettivamente. E ciò indipendentemente dal valore assunto da ρ.
Variabili aleatorie caratterizzate dalla densità di probabilità congiunta (130) si dicono gaussiane
miste.
La loro peculiarità risiede nel fatto che per esse l’incorrelazione implica la statistica indipendenza
(proprietà questa che, abbiamo detto più sopra, non vale in generale). Se infatti si calcola il
coefficiente di correlazione, utilizzando la (118), si trova:
ρ XY = ρ
(132)
Le variabili, dunque, sono incorrelate quando ρ = 0. D’altro canto, dalla (130) si vede che per ρ = 0
la densità di probabilità congiunta diventa:
32
f XY ( x, y ) =
⎪⎧ ⎡ ( x − mX ) 2 ( y − mY ) 2 ⎤ ⎪⎫
exp ⎨− ⎢
+
⎥ ⎬ = f X ( x ) fY ( y )
2
2πσ X σ Y
2σ Y2 ⎦ ⎭⎪
⎩⎪ ⎣ 2σ X
1
(133)
con ciò confermando l’asserto precedente.
*****
Estensione al caso di n variabili.
Quanto detto per una coppia di variabili può ovviamente essere esteso ad un numero qualsiasi di
variabili aleatorie X1, X2, …, Xn. Per esse si potrà allora definire, ad esempio, una densità di
probabilità congiunta f X1 X 2 ... X n ( x1 , x2 ,..., xn ) che nel caso in cui le variabili siano tutte tra loro
statisticamente indipendenti si riduce al prodotto delle densità di probabilità marginali:
f X1 X 2 ... X n ( x1 , x2 ,..., xn ) = f X1 ( x1 ) f X 2 ( x2 )
f X n ( xn )
(134)
Definita anche in questo caso la funzione caratteristica, nella stessa ipotesi di indipendenza statistica
essa sarà pari al prodotto delle funzioni caratteristiche marginali:
C X1 X 2 ... X n (u1 , u2 ,..., un ) = C X1 (u1 )C X 2 (u2 )
C X n (u n )
(135)
Per ricavare, a partire dalla (134), la densità di probabilità di una delle variabili sarà sufficiente
saturare tutte le altre; ad esempio:
+∞
f X1 ( x1 ) =
+∞
∫ ∫
x2 =−∞ x3 =−∞
+∞
∫
xn =−∞
f X1 X 2 ... X n ( x1 , x2 ,..., xn )dx2 dx3 … dxn
(136)
In realtà, se la (134) ha il significato di densità di probabilità congiunta di ordine n, è chiaro che, a
partire da essa, possono essere definite densità di probabilità congiunte di ordine k < n che
includono k delle n variabili assegnate. Per determinare la generica di queste densità si dovrà
integrare la (134) nel dominio di definizione delle (n – k) variabili complementari.
Al di là degli aspetti formali, questa generalizzazione al caso di n variabili (o, per meglio dire, di
variabile aleatoria n-dimensionale) è piuttosto ovvia, e non sembra necessario insistere su di essa,
poiché ciò non aggiungerebbe nulla alla comprensione.
*****
Funzioni di due variabili aleatorie
Consideriamo preliminarmente un caso particolare.
Sia:
Z = X +Y
(137)
Si vuol esplicitare la densità di probabilità della variabile Z. Peraltro, conviene dapprima
considerare la distribuzione di probabilità cumulativa che, con ovvia notazione, potrà scriversi:
FZ ( z ) = Pr {Z ≤ z} = Pr { X + Y ≤ z}
(138)
33
Si guardi allora alla Figura 10.
y
z
z
x
x+y<z
y=z−x
Figura 10
La regione del piano x-y favorevole all’evento definito nella (138) è quella al di sotto della retta y =
z – x; Ne consegue che FZ(z) potrà essere calcolata integrando la densità di probabilità congiunta,
fXY(x,y) delle variabili X e Y in tale regione. Formalmente:
FZ ( z ) =
∫∫
+∞
f XY ( x, y )dxdy =
x+ y≤ z
z−x
∫ ∫
f XY ( x, y )dxdy
(139)
x =−∞ y =−∞
Dalla (139) è poi immediato ricavare la fZ(z), ricordando il legame che c’è tra la densità di
probabilità e la distribuzione di probabilità congiunta:
fZ ( z) =
+∞ z − x
⎤ +∞
dFZ ( z ) d ⎡
= ⎢ ∫ ∫ f XY ( x, y )dxdy ⎥ = ∫ f XY ( x, z − x)dx
dz
dz ⎢⎣ x =−∞ y =−∞
⎥⎦ −∞
(140)
avendo utilizzato un noto risultato dell’analisi matematica, in virtù del quale la derivata di un
integrale rispetto all’estremo superiore di integrazione è uguale alla funzione integranda calcolata in
tale estremo.
Un caso ulteriormente particolare si verifica quando le variabili X e Y sono tra loro statisticamente
indipendenti. Allora la (140) può riscriversi:
+∞
fZ ( z) =
∫
f X ( x) fY ( z − x)dx
(141)
−∞
che ha evidentemente il significato di integrale di convoluzione tra le densità di probabilità dei
singoli addendi della (137).
La (139) può ovviamente essere generalizzata. Considerata una generica funzione:
Z = g( X ,Y )
(142)
e indicato con D(z) il dominio del piano x-y in corrispondenza del quale risulta Z ≤ z, si potrà
scrivere:
34
FZ ( z ) =
−1
+∞ g ( z , x )
∫∫
∫
f XY ( x, y )dxdy =
∫
f XY ( x, y )dxdy
(143)
x =−∞ y =−∞
D( z)
avendo indicato con g−1(Z, X) la funzione inversa della (142) rispetto a Y. Ovviamente, sia nella
(139) che nella (143) è ugualmente lecito considerare la funzione inversa rispetto a X, nel qual caso
la (143), ad esempio, si scrive:
−1
+∞ g ( z , y )
FZ ( z ) =
∫
∫
f XY ( x, y )dxdy
(144)
y =−∞ x =−∞
Derivando la (143) o la (144) si ottiene infine:
d ⎡
fZ ( z) = ⎢ ∫
dz ⎢⎣ x =−∞
−1
+∞ g ( z , x )
∫
y =−∞
⎤ d ⎡ +∞ g ( z , y )
⎤
f XY ( x, y )dxdy ⎥ = ⎢ ∫
f
(
x
,
y
)
dxdy
⎥
∫ XY
⎥⎦ dz ⎢⎣ y =−∞ x =−∞
⎥⎦
−1
(145)
E’ importante evidenziare che ai fini del calcolo degli indicatori statistici (valore medio, valore
quadratico medio, varianza, momenti di ordine superiore,…) della variabile Z fornita dalla (142) il
calcolo della densità di probabilità fZ(z) non è indispensabile, ma è sufficiente la conoscenza della
fXY(x,y). Per valor medio e varianza, in particolare, valgono le seguenti relazioni:
+∞
mZ = g ( X , Y ) =
+∞
∫ ∫
(146a)
g ( x, y ) f XY ( x, y ) dxdy
x =−∞ y =−∞
σ Z2 = ⎡⎣ g ( X , Y ) − g ( X , Y ) ⎤⎦
2
+∞
+∞
∫ ∫
=
2
x =−∞ y =−∞
⎡⎣ g ( x, y ) − g ( x, y ) ⎤⎦ f XY ( x, y )dxdy
(146b)
In particolare, nel caso della (137) (quando cioè la funzione g(X,Y) è una somma), la (146a)
fornisce:
+∞
mZ =
+∞
∫ ∫
+∞
( x + y ) f XY ( x, y )dxdy =
x =−∞ y =−∞
=
+∞
+∞
−∞
−∞
∫ xdx ∫
+∞
∫ ∫
+∞
xf XY ( x, y )dxdy +
x =−∞ y =−∞
f XY ( x, y )dy +
+∞
+∞
−∞
−∞
∫ ydy ∫
∫ ∫
yf XY ( x, y )dxdy =
x =−∞ y =−∞
+∞
f XY ( x, y )dx =
+∞
∫ xf
−∞
+∞
X
( x)dx +
∫ yf
Y
(147)
( y )dy = mX + mY
−∞
Il valor medio della somma di due variabili aleatorie è dunque sempre uguale alla somma dei valori
medi delle variabili singole.
Sempre per la (137), la (146b) fornisce invece (tenendo conto della (147)):
35
σ z2 =
+∞
∫
+∞
∫ (x + y − m X
x = −∞ y = −∞
+∞
+
∫
+∞
− mY )2 f XY ( x, y )dxdy =
∫
+∞
∫ (x − m X )
2
f XY ( x, y )dxdy +
x = −∞ y = −∞
+∞
+∞
2
∫ ( y − mY ) f XY ( x, y)dxdy + 2 ∫
x = −∞ y = −∞
+∞
∫ (x − m X )( y − mY ) f XY ( x, y)dxdy =
(148)
x = −∞ y = −∞
= σ X2 + σ Y2 + 2σ 11
Solo nel caso di variabili incorrelate, dunque, la varianza della somma di due variabili aleatorie è
pari alla somma delle varianze delle variabili singole.
I risultati qui verificati nel caso di una coppia di variabili possono essere estesi alla somma di un
numero arbitrario di variabili, semplicemente iterandone le conclusioni. In particolare è sempre vero
che il valor medio della somma è uguale alla somma dei valori medi, mentre la sommabilità delle
varianze è subordinata all’ipotesi di incorrelazione. In particolare, le varianze si sommano nel caso
di variabili statisticamente indipendenti (essendo la statistica indipendenza condizione più restrittiva
dell’incorrelazione).
Un altro risultato importante riguarda la funzione caratteristica: se le variabili X e Y sono
statisticamente indipendenti, allora la funzione caratteristica della variabile Z = X + Y è essa pure
uguale al prodotto delle funzioni caratteristiche CX(u) e CY(u) (in questo caso nell’unica variabile
formale u). In formula:
CZ (u ) = C X (u )CY (u )
(149)
Anche la verifica di questa proprietà è immediata. Dalla definizione, infatti, risulta:
+∞
CZ (u ) = exp(iuz ) = exp(iu ( x + y )) =
+∞
∫ ∫
exp [iu ( x + y )] f XY ( x, y )dxdy =
x =−∞ y =−∞
+∞
=
∫ exp(iux) f
−∞
+∞
X
( x)dx ⋅ ∫ exp(iuy ) fY ( y )dy = C X (u )CY (u )
−∞
V’è un modo alternativo per ricavare la densità di probabilità di Z. E’ significativo introdurlo con
riferimento ad una situazione più generale (donde il caso discusso in questa sezione potrà essere
ottenuto per particolarizzazione).
*****
Funzioni di n variabili aleatorie
Assegnato un insieme, di dimensione arbitraria, di variabili aleatorie X1, X2,…, Xn, con densità di
probabilità congiunta f X1 , X 2 ,…, X n ( x1 , x2 ,… , xn ) , e dato un insieme parimenti numeroso di variabili Y1,
Y2,…, Yn, funzioni delle precedenti, si dimostra che vale la seguente relazione:
fY1 ,Y2 ,…,Yn ( y1 , y2 ,..., yn ) = f X1 , X 2 ,…, X n ( x1 , x2 ,..., xn )
∂ ( x1 , x2 ,..., xn )
∂ ( y1 , y2 ,..., yn )
(150)
utilizzando la quale è possibile esplicitare la densità di probabilità congiunta delle variabili Y1,
Y2,…, Yn, a partire dalla conoscenza della densità di probabilità congiunta delle variabili X1, X2,…,
Xn. Nella (150), il simbolo ⏐∂(x1, x2,…, xn)/∂(y1, y2,…, yn)⏐ indica il modulo del determinante
36
Jacobiano delle xj rispetto alle yk, pari all’inverso del modulo del determinante Jacobiano delle yk
rispetto alle xj:
∂ ( x1 , x2 ,..., xn )
∂ ( y1 , y2 ,..., yn )
⎡ ∂x1
⎢ ∂y
⎢ 1
⎢ ∂x2
= det ⎢⎢ ∂y1
⎢
⎢
⎢ ∂xn
⎢⎣ ∂y1
∂x1
∂y2
∂x2
∂y2
∂xn
∂y2
∂x1 ⎤
∂yn ⎥
⎥
∂x2 ⎥
∂yn ⎥
⎥
⎥
⎥
∂xn ⎥
∂yn ⎥⎦
(151)
Chiaramente, le derivate che compaiono nella (151) possono essere esplicitate a partire dalle singole
relazioni funzionali che legano le variabili Xj alle variabili Yk:
X 1 = g1 (Y1 , Y2 ,… , Yn )
X 2 = g 2 (Y1 , Y2 ,… , Yn )
(152)
…
X n = g n (Y1 , Y2 ,… , Yn )
Essendo interessati a calcolare la densità marginale di una delle variabili Yk, con procedura analoga
a quella già descritta in precedenza per un problema analogo, si tratterà di saturare la densità di
probabilità congiunta rispetto alle n – 1 variabili complementari.
Esempio
Si consideri una coppia di variabili aleatorie gaussiane miste, X1 e X2, con valori medi nulli ed
identica varianza σX2; utilizzando la (130), la densità di probabilità congiunta delle due variabili può
scriversi:
f X1 X 2 ( x1 , x2 ) =
1
2πσ
2
X
⎡
⎤
1
exp ⎢ − 2
x 2 + x22 − 2 ρ x1 x2 ) ⎥
2 ( 1
1− ρ
⎣ 2σ X (1 − ρ )
⎦
Siano Y1 = R e Y2 = Θ due variabili aleatorie legate a X1 e X2 dalle seguenti relazioni:
R = X 12 + X 22
⎛X ⎞
Θ = tan −1 ⎜ 2 ⎟
⎝ X1 ⎠
Invertendo le precedenti si ottiene:
X 1 = R cos(Θ)
X 2 = R sin(Θ)
da cui il modulo del determinante Jacobiano si calcola immediatamente, fornendo:
37
∂ ( x1 , x2 )
∂ ( y1 , y2 )
⎡ ∂x1
⎢ ∂r
= det ⎢
⎢ ∂x2
⎢⎣ ∂r
∂x1 ⎤
⎡cos(θ )
∂θ ⎥
⎥ = det ⎢
∂x2 ⎥
⎣ sin(θ )
⎥
∂θ ⎦
− r sin(θ ) ⎤
=r
r cos(θ ) ⎦⎥
Utilizzando la (150) si ha allora:
f RΘ ( r , θ ) =
r
2πσ X2
⎧
⎫
r2
exp ⎨ − 2
1 − 2 ρ cos(θ ) sin(θ ) ]⎬
2 [
1− ρ
⎩ 2σ X (1 − ρ )
⎭
Nel caso ρ = 0 (che corrisponde a variabili X1 e X2 tra loro incorrelate, e quindi indipendenti), la
precedente fornisce:
⎛ r2 ⎞
r
f RΘ ( r , θ ) =
exp ⎜ − 2 ⎟
2πσ X2
⎝ 2σ X ⎠
Questa funzione dipende, come si vede, dalla sola variabile r. Valori di X1 e X2 da −∞ a +∞ vengono
evidentemente convertiti dalla trasformazione in: 0 ≤ R < +∞ e −π < Θ ≤ π.
La densità di probabilità di R può essere ottenuta come:
π
f R (r ) =
∫
f RΘ (r ,θ )dθ =
−π
π
⎛ r2 ⎞
⎛ r2 ⎞
r
r
d
exp
θ
exp
−
=
⎜
⎟
⎜− 2 ⎟
∫ 2πσ X2 ⎝ 2σ X2 ⎠
σ X2
⎝ 2σ X ⎠
−π
Si tratta dunque di una variabile di Rayleigh.
La densità di probabilità di Θ può essere ottenuta come:
f Θ (θ ) =
+∞
∫
f RΘ (r ,θ )dr =
0
+∞
∫
0
⎛ r2
r
exp
⎜− 2
2πσ X2
⎝ 2σ X
⎞
1
⎟ dr =
2π
⎠
Si tratta dunque di una variabile aleatoria uniforme. Osserviamo anche che l’ipotesi di statistica
indipendenza delle variabili X1 e X2 si trasferisce a R e Θ che sono infatti, a loro volta,
statisticamente indipendenti.
*****
Il teorema-limite centrale
Consideriamo la variabile aleatoria:
n
Zn = ∑ X j
(153)
j =1
e supponiamo che le n variabili aleatorie X1, X2, …, Xn:
ƒ
ƒ
siano tra loro statisticamente indipendenti,
abbiano tutte uguale densità di probabilità f X j ( x j ) = f ( x ) , con valore medio m X j = m e
varianza σ X2 j = σ 2 .
38
Nelle ipotesi poste, nessuna delle variabili risulta, per così dire, “dominante” rispetto alle altre.
La densità di probabilità della variabile Zn può essere calcolata utilizzando gli strumenti analitici
descritti più sopra. Nondimeno, ciò che vogliamo chiederci è se sia possibile individuare
l’andamento di tale densità di probabilità per valori di n molto elevati (al limite → ∞).
Innanzitutto osserviamo che il valore medio di Zn, indicato con mn, è pari ad n volte il valore medio
m; come verificato in precedenza, la proprietà secondo cui il valore medio della somma è pari alla
somma dei valori medi è una proprietà generale, e prescinde dall’ipotesi di indipendenza statistica
delle variabili. Al contrario, l’ipotesi di indipendenza statistica 6 è necessaria per affermare che la
varianza di Zn, indicata con σn2, è pari ad n volte la varianza σ2. In ogni caso si può scrivere:
mn = n ⋅ m
(154a)
σ n2 = n ⋅ σ 2
(154b)
A partire dalla (153), definiamo ora la variabile normalizzata:
Sn =
Z n − mn
σn
=
Zn − n ⋅ m
n ⋅σ
(155)
Indipendentemente da n, è chiaro che Sn ha valor medio nullo e varianza unitaria (variabile
normalizzata). A parte queste differenze, Sn ha le stesse proprietà statistiche di Zn, in particolare lo
stesso andamento della densità di probabilità.
La risposta al problema sopra formulato, e cioè il calcolo della densità di probabilità per n → ∞ è
fornita dal seguente enunciato del teorema-limite centrale introdotto dal matematico russo
Lyapunov 7 :
La densità di probabilità della variabile somma normalizzata Sn tende a una variabile gaussiana con
valor medio nullo e varianza unitaria; si ha cioè:
lim f Sn ( sn ) =
n →∞
⎛ s2 ⎞
1
exp ⎜ − n ⎟
2π
⎝ 2⎠
(156)
In pratica, questo risultato asserisce che la somma di un gran numero di variabili aleatorie
indipendenti segue, con buona approssimazione, una legge gaussiana, e ciò indipendentemente dalla
particolare distribuzione di ciascuna di esse. Il teorema-limite centrale sarà molto utile in una
dispensa successiva in cui modelleremo un fenomeno fisico estremamente importante per le
applicazioni: il rumore termico.
Si può avere un’idea della tendenza alla variabile gaussiana esaminando un caso particolare. In
Figura 11 sono riportate le densità si probabilità di Sn, per valori crescenti di n, nel caso di variabili
Xj uniformi. Ricordando quanto detto nel caso di due variabili statisticamente indipendenti, la
densità di probabilità della somma si ottiene dalla convoluzione iterata, n – 1 volte, della densità di
probabilità f(x); l’andamento gaussiano risulta del tutto evidente, per l’esempio, già con n = 15. Si
noti che in figura la densità di probabilità gaussiana è stata indicata come normale, essendo questa
una classica dicitura alternativa per la funzione densità gaussiana.
6
In realtà è sufficiente l’ipotesi di incorrelazione che però è implicata, come noto, da quella di statistica indipendenza.
In realtà del teorema-limite centrale si possono fornire enunciati molto più generali; ad esempio si verifica che
l’ipotesi di avere densità di probabilità tutte uguali tra loro non è essenziale ai fini della dimostrazione. Qui ci si è
limitati a ricordare quanto utile per la trattazione di argomenti successivi nell’ambito del Corso.
7
39
Figura 11
40