NOME: ……………………………………………………… CLASSE: …………………………………….…………
COGNOME: ………………………………………………… DATA: ……………………………………….…………
Verifica di geometria – Quadrilateri
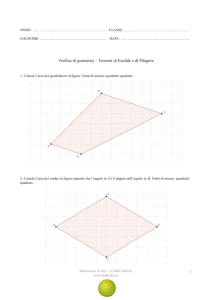
1. Dì che figura è il quadrilatero seguente e disegna l’altezza passante per A relativa al lato CD.
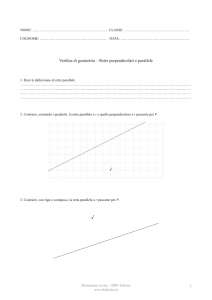
2. Trova tutti gli angoli interni del trapezio in figura. Oltre a essere una diagonale cos’altro è AC?
Matematica in rete – © BBN Editrice
www.didasfera.it
1
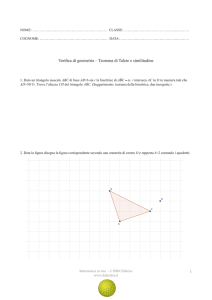
3. Dato il parallelogramma ABCD disegna con riga e compasso le altezze relative al lato AD e CD passanti per B.
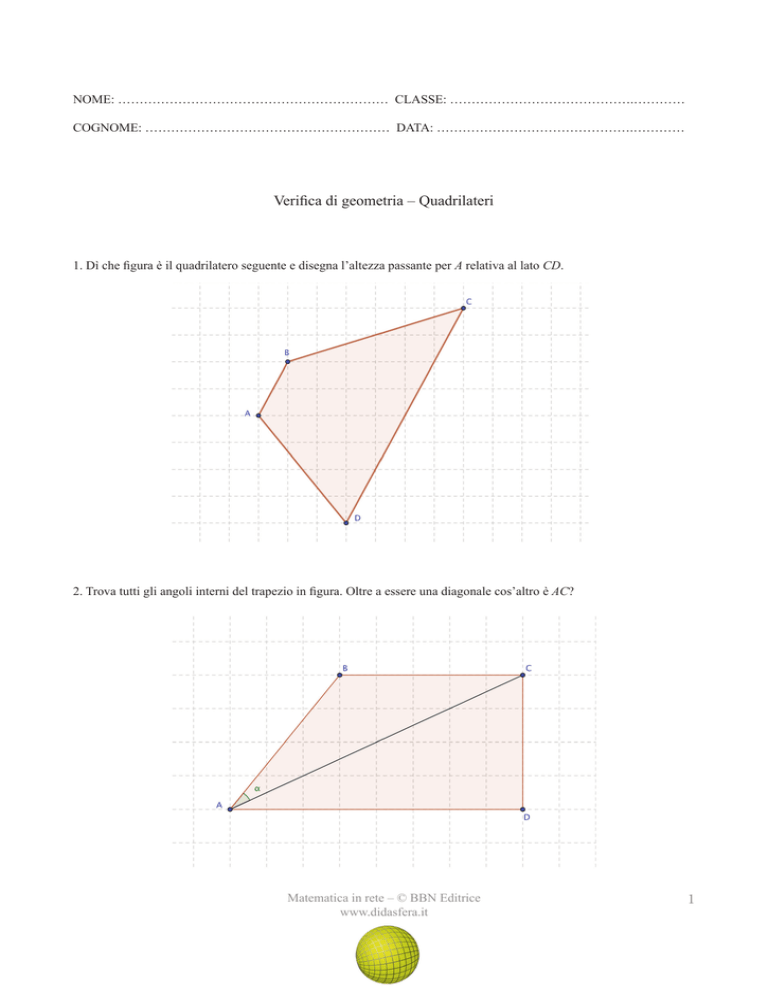
4. Trova tutti gli angoli interni del rombo ABCD.
5. Indica quali sono i quadrilateri che hanno un centro di simmetria, quali hanno assi di simmetria e quanti assi di
simmetria hanno.
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
Matematica in rete – © BBN Editrice
www.didasfera.it
2
6. Dimostra che se un trapezio ha gli angoli alla base congruenti allora è isoscele.
IPOTESI: ………………………………………
TESI: …………………………………………..
DISEGNO:
DIMOSTRAZIONE: ………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
7. Dimostra che se un quadrilatero ha gli angoli opposti congruenti allora è un parallelogramma.
IPOTESI: ………………………………………
TESI: …………………………………………..
DISEGNO:
DIMOSTRAZIONE: ………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
Matematica in rete – © BBN Editrice
www.didasfera.it
3
8. Dato il rettangolo ABCD traccia la retta passante per O centro di simmetria che incontra AB in H e CD in K. Siano
M ed N i punti medi di AD e BC. Dimostra che MKNH è un parallelogramma.
IPOTESI: ………………………………………
TESI: …………………………………………..
DISEGNO:
DIMOSTRAZIONE: ………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
9. Dato un rombo ABCD prolunga AB di un segmento BE dal lato di B. Sia r la bisettrice dell’angolo CB̂E .
Dimostra che r è parallela alla diagonale AC.
IPOTESI: ………………………………………
TESI: …………………………………………..
DISEGNO:
DIMOSTRAZIONE: ………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
Matematica in rete – © BBN Editrice
www.didasfera.it
4