NOME: ……………………………………………………… CLASSE: …………………………………….…………
COGNOME: ………………………………………………… DATA: ……………………………………….…………
Verifica di geometria – Rette perpendicolari e parallele
1. Dare la definizione di rette parallele.
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
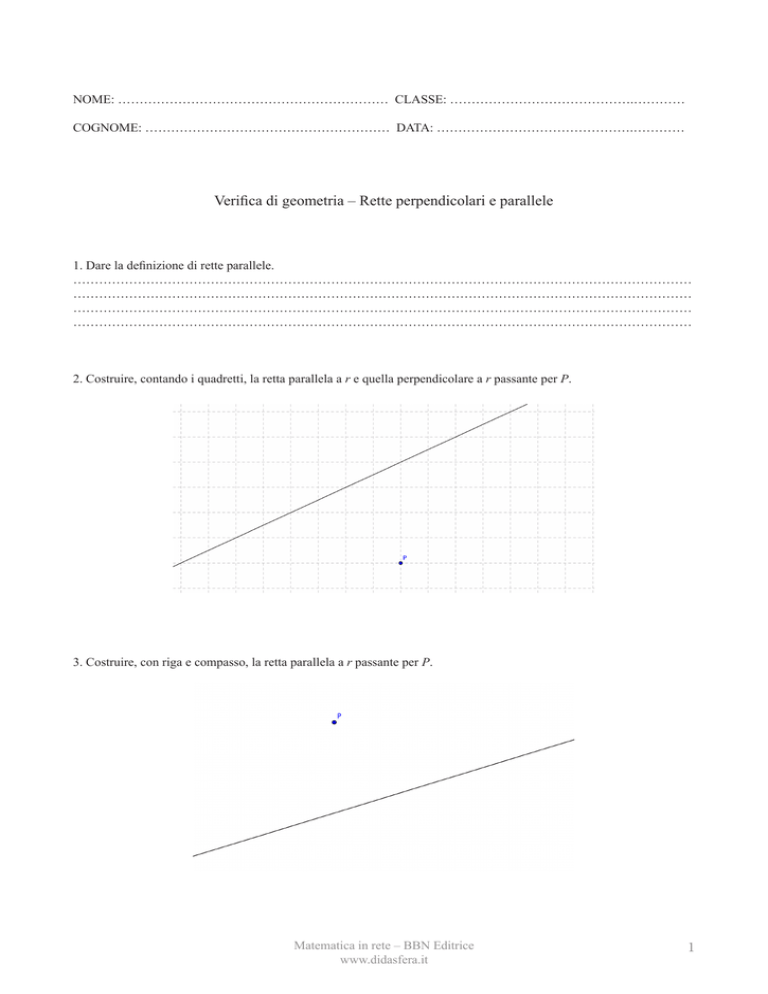
2. Costruire, contando i quadretti, la retta parallela a r e quella perpendicolare a r passante per P.
3. Costruire, con riga e compasso, la retta parallela a r passante per P.
Matematica in rete – BBN Editrice
www.didasfera.it
1
4. Dire cosa è un fascio proprio e cosa è un fascio improprio.
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
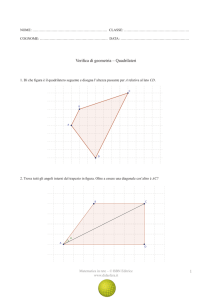
5. Completare in base alla figura.
α e α’ sono angoli ………………………………………
β e δ’ sono angoli ………………………………………
α e δ’ sono angoli ………………………………………
δ e α’ sono angoli ………………………………………
δ e β’ sono angoli ………………………………………
α’ e γ’ sono angoli ……………………………………...
6. Sempre in riferimento al disegno dell’esercizio precedente dire se gli angoli sono congruenti o supplementari.
α e α’ sono angoli ………………………………………
β e δ’ sono angoli ………………………………………
α e δ’ sono angoli ………………………………………
δ e α’ sono angoli ………………………………………
δ e β’ sono angoli ………………………………………
α’ e γ’ sono angoli ……………………………………...
Matematica in rete – BBN Editrice
www.didasfera.it
2
7. Date le rette r e s e il punto P traccia le proiezioni di P su r e su s contando i quadretti e chiamale rispettivamente A e
B. Dire quanto vale la somma degli angoli AP̂B + AĈB e perché.
8. Trova A’B’ proiezione di AB su r con riga e compasso.
Matematica in rete – BBN Editrice
www.didasfera.it
3
9. Data la figura seguente sapendo che CÂB = 2α calcola l’angolo AD̂C.
10. Dato un triangolo isoscele ABC di base BC si tracci una semiretta di origine A parallela alla base BC. Si dimostri che
tale semiretta è bisettrice dell’angolo esterno dell’angolo BÂC .
IPOTESI: ………………………………………
TESI: …………………………………………..
DISEGNO:
DIMOSTRAZIONE: ………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
Matematica in rete – BBN Editrice
www.didasfera.it
4
11. Prolungare il lato AB di un triangolo ABC, isoscele sulla base BC, di un segmento AD≅AB. Dimostra che BĈD è
retto.
IPOTESI: ………………………………………
TESI: …………………………………………..
DISEGNO:
DIMOSTRAZIONE: ………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
Matematica in rete – BBN Editrice
www.didasfera.it
5