Probabilità e statistica

Liceo Scientifico Statale
“ Renato Caccioppoli ”
di Scafati
Dipartimento di Matematica e Fisica
Seminari di matematica 2000
Quaderno di appunti:
Probabilità e
Luigi Panariello
statistica
Luigi PANARIELLO: Probabilità e statistica
pag. 2
SOMMARIO
1.
CONCETTO ELEMENTARE DI INSIEME.......................................................................................................................3
1.1
2.
PRODOTTO CARTESIANO FRA DUE O PIU’ INSIEMI........................................................................................4
CONCETTO ELEMENTARE DI PROBABILITA’ NEGLI INSIEMI FINITI..................................................................5
1.2
3.
Probabilità di un evento................................................................................................................................................5
PROPRIETA’ ELEMENTARI DELLA FUNZIONE DI PROBABILITA’........................................................................6
1.3
Esempi di problemi risolti ............................................................................................................................................6
4.
INDIPENDENZA ................................................................................................................................................................8
5.
PROBABILITA’ CONDIZIONATA...................................................................................................................................8
6.
IL TEOREMA DI BAYES ..................................................................................................................................................9
7.
LE MEDIE NUMERICHE ................................................................................................................................................10
1.4
SCARTI .....................................................................................................................................................................10
8.
MODA E MEDIANA ........................................................................................................................................................11
9.
VARIABILI CASUALI .....................................................................................................................................................12
10.
SISTEMI DI DUE VARIABILI CASUALI ..................................................................................................................13
11.
LA LEGGE DEI GRANDI NUMERI............................................................................................................................15
12.
DISTRIBUZIONE BINOMIALE (di Bernoulli) ...........................................................................................................16
Luigi PANARIELLO: Probabilità e statistica
pag. 3
1. CONCETTO ELEMENTARE DI INSIEME
Ogni elenco o collezione di oggetti del pensiero e detta “INSIEME”. Gli oggetti che lo compongono sono detti
“ELEMENTI”. Per indicare che x è un elemento dell’insieme S si scrive x∈S, mentre y∉S significa che y non è elemento
di S.
Si dice che l’insieme A è parte dell’insieme B, ov vero che è incluso oppure contenuto in B, se x∈A implica che x∈B, ed in
tal caso si scrive A⊆B. Se A è incluso in B può anche capitare che A=B. Se però A è diverso da B ed è incluso in B si dice
che è “strettamente incluso in B” oppure che è “parte propria” di B e si può scrivere A⊂B.
Alcuni insiemi particolarmente importanti in matematica sono:
•
N0 insieme dei numeri naturali 0,1,2,3,…
•
N insieme dei numeri naturali positivi 1,2,3,…
•
Z insieme dei numeri interi …,-3,-2,-1,0,1,2,3,…
•
Q insieme dei numeri razionali (un numero razionale è una classe di frazioni equivalent, comprende lo zero e numeri
positivi e negativa. di solito N e Z vengono considerati parti di Q)
•
R insieme dei numeri reali
•
insieme dei numeri complessi
• ∅ insieme vuoto, privo di qualunque elemento
A volte un insieme viene specificato facendo l’elenco degli elementi (caso finito) o formulando la proprietà che caratterizza
gli elementi dell’insieme. Nel seguente esempio lo stesso insieme A viene descritto in due modi:
A = {2,4,6,8} = {x∈N: x è pari e x<10}
Per un insieme finito A è possibile contare il numero di oggetti, ottenendo un numero chiamato ORDINE di A (oppure
CARDINALITA’ di A). Tale numero verrà indicato con |A|
Dati due insiemi A, B inclusi in un insieme “ambiente” S, si pone:
A∪B = {x∈S: x∈A oppure x∈B} detto UNIONE di A e B.
Se risulta A∪B=S si dice A,B RICOPRONO S
A∩B = {x∈S: x∈A e x∈B} detto INTERSEZIONE di A e B. Se risulta
A∩B= ∅ si dice che A,B sono DISGIUNTI.
A-B = {x∈S: x∈A e x∉B} detto DIFFERENZA fra A e B (o meglio
complementare di B in A)
Ac = {x∈S: x∉A } detto COMPLEMENTARE DI A (in S)
Luigi PANARIELLO: Probabilità e statistica
pag. 4
Se A,B,C,… sono parti di S a due a due disgiunte e la loro unione ricopre S si dice che esse formano una PARTIZIONE
DELL’INSIEME S. Le leggi fondamentali che regolano le operazioni fra insiemi sono:
Leggi di idempotenza
A∩A=A
(A∩B) ∩C = A∩(B ∩C)
Leggi associative
Leggi commutative
A∩B = B∩A
A∩(B ∪C) = (A∩B) ∪( A∩C)
Leggi distributive
Leggi di identità
Leggi di complementarietà
Leggi di De Morgan
A∩S = A
A ∪Ac = S
A∩Ac = ∅
e
A∩∅=∅
Sc = ∅
(A∪B)c = Ac ∩Bc
∅c = S,
(A∩B)c = Ac ∪Bc
Osservazioni e primi esercizi:
1.
2.
Illustrare graficamente, ove possibile, le leggi fondamentali riportate nella precedente tabella
Ripartire il set S dei 26 simboli alfabetici minuscoli in una PARTIZIONE composta da tre parti aventi qualche
significato linguistico
3.
Nell’ambiente N (numeri naturali, {0,1,2,…}, posto A={0,2,4,6,8,…}={x ∈N/ x è pari}, B={1,3,5,7,…}= {x ∈N/ x è
dispari}, risulta che A, B formano una partizione di N. Trovare altre tre partizioni di N
In maniera elementare un insieme viene definito “FINITO” se i sui oggetti si possono contare (altrimenti viene
definito “INFINITO”). L’insieme vuoto si annovera ovviamente fra gli insie mi finiti (con numero zero di oggetti). Si
può dimostrare che la minima numerosità infinita è quella di N (tale numerosità è detta “numerabile”).
Ad esempio i vertici di un poligono costituiscono un insieme finito, ma i punti di uno dei suoi lati sono infiniti.
Si noti, nell’esempio 2, che A e B sono infiniti, pur essendo parti proprie di N. Un insieme infinito può avere lo
stesso numero di oggetti di una sua parte propria.
4.
5.
6.
7.
Dire quale dei seguenti insiemi è vuoto. A={x∈N/ x è pari e primo}, B={x∈R/ x > x}, C={x∈
(Risposta: B)
8.
Dato A={a,b,c}, dire quale scritture è sbagliata: (1) ∅∈A , (2) ∅ ⊆ A , (3) ∅ ⊂ A (R. 1)
9.
Se A⊆B, B⊆C, C⊆A, quale conseguenza ne possiamo trarre?
1.1
x2+1 = 0}
(R. A=B=C)
PRODOTTO CARTESIANO FRA DUE O PIU’ INSIEMI
Una operazione un po’ più complessa fra gli insiemi è il cosiddetto prodotto cartesiano. Dati due insiemi A e B, consideriamo
tutte le “COPPIE ORDINATE” (a,b) costituite da due elementi a,b presi nell’ordine di scrittura nelle parentesi tonde, con
a∈A e b∈B. L’insieme di tutte le coppie forma un nuovo insieme indicato con AxB e detto “PRODOTTO (cartesiano)” di A
per B.
Se uno dei due insiemi è vuoto il prodotto si assume vuoto per definizione.
Si noti che AxB ≠ BxA (salvo il caso in cui non sia A=B, ed in tal caso si può scrivere AxB = AxA = A2). L’ambiente di AxB
è quello di S2, in quanto avendosi a∈A e b∈B, sarà anche a,b∈S cosicché (a,b)∈SxS = S2
Osservazioni e primi esercizi:
•
Costruire AxB, ove A={1,2,3} e B={p,q,r,s}. Notare che AxB ha 12 elementi e che quindi vale il PRINCIPIO DI
MOLTIPLICAZIONE (il numero di oggetti di AxB è il numero di A per il numero di B, sempre che A e B siano
entrambi finiti). Quindi |AxB| = |A| |B|
•
Se uno dei due insiemi A,B è infinito, e l’altro è non vuoto, anche AxB è infinito.
•
Se in geometria analitica consideriamo l’asse x come asse reale R’ e l’asse y come una copia dell’asse reale R’’, i
punti del piano sono rappresentati da coppie di coordinate del tipo (x,y) con x∈R’ e y ∈R’’ e pertanto il piano
cartesiano si rappresenta mediante il prodotto cartesiano R’xR’’ che equivale ad R 2.
•
Se consideriamo n insiemi A1, A2, A3 ,….,A n, possiamo costruire tutte le n-ple ordinate (a1, a2, a3 ,….,a n), ove si
intende che a1∈ A1, a2∈ A2,…, a n∈ An. In tal caso otteniamo il prodotto cartesiano degli n insiemi, indicato con
A1xA2xA3x….xA n. Se gli n insiemi sono uguali ad A otteniamo AxAx…A = A n
•
Ad esempio un riferimento cartesiano tridimensionale Oxyz (delle spazio) coordina lo spazio su R3, e ogni punto si
rappresenta con una terna di coordinate (x,y,z) (chiamate rispettivamente ascissa, ordinata e quota)
•
Il prodotto cartesiano degli insiemi A1, A2, A3 ,….,A n, è costituito da k oggetti, essendo k=k1k2…k n il prodotto delle
numerosità ki singoli insiemi Ai. Quindi |A1xA2xA3x….xA n|= |A1||A2||A3|….|A n| e |An!=!A|n
Luigi PANARIELLO: Probabilità e statistica
pag. 5
2. CONCETTO ELEMENTARE DI PROBABILITA’ NEGLI INSIEMI FINITI
Supponiamo che tutti i possibili esiti di un dato esperimento, ovvero di una data prova o di una possibile eventualità, vengano
considerati come un insieme S (che viene chiamato spesso “S PAZIO CAMPIONARIO” oppure “SPAZIO DEGLI EVENTI”
ovvero “SPAZIO DELLE PROBABILITA’” e con altri nomi similari). Un singolo punto o elemento di S è quindi un evento
elementare.
Ad esempio se lanciamo un dado standard a 6 facce numerate da 1 a 6 e consideriamo come evento elementare l’uscita di un
numero compreso fra 1 e 6, potremmo porre S={1,2,3,4,5,6}.
Se invece lanciamo due dadi, uno rosso e l’altro nero (per distinguerli), e conveniamo di indicare l’uscita come “coppia di
numeri” (r,n), dove r è il nume ro dato dal rosso e b è il numero dato dal bianco, allora lo spazio campionario sarà S=A2 =
AxA (se poniamo A ={ x∈N/ 1 ≤ x ≤ 6})
Facciamo il caso che S sia un insieme finito e che per ogni suo per ogni evento elementare x∈S sia stata definita una
“probabi lità” p(x), cioè un numero reale p(x) compreso nell’intervallo [0,1], cioè 0 ≤ p(x) ≤ 1, in maniera che la somma di
tutte le probabilità p(x) al variare di x in tutto S, sia 1. Possiamo quindi definire gli SPAZI DI PROBABILITA’ S FINITI con
le seguenti tre caratteristiche:
•
Lo spazio degli eventi S è finito
•
Per ogni x∈
∈S è definito il numero reale p(x) ∈R, con 0 ≤ p(x) ≤ 1, detto “probabilità dell’evento elementare x”
•
∑ p( x ) = 1
x∈S
Se p(x)=p(y) per ogni scelta di x,y in S, si dice che lo spazio è EQUIPROBABILE ovvero che gli eventi stessi sono
equiprobabili
In tal casi risulta
p ( x) =
1
, dove |S| è l’ordine di S.
|S|
Consideriamo ad esempio il lancio del dado. S={1,2,3,4,5,6} e quindi |S|=6.
•
Se consideriamo un dado “ideale” in cui non vi sia motivo di ritenere che la probabilità di uscita di una faccia possa
superare quella di un’altra faccia, vuol dire che dovremo considerare uno spazio EQUIPROBABILE in cui si avrà
p(1) = p(2) = … = p(6) =
•
1
6
(*) Se però abbiamo motivo di ritenere che lo spazio non sia equiprobabile, non potremo assumere la stessa
probabilità per ciascun evento elementare e quindi dovremo procedere diversamente. I modi di procedere NON
APPARTENGONO DI PER SE AL CALCOLO DELLE PROBABILITA’, potendo dipendere anche da
considerazioni del tutto soggettive. Ad esempio si potranno fare dei calcoli molto sofisticati sul bilanciamento
meccanico del dado, sull’attrito nell’aria, sull’elasticità del tavolo ecc. In tal caso può intervenire in maniera
sostanziale la bravura del calcolatore. Tuttavia vi è un metodo “empirico” abbastanza accettabile (che comunque non
rientra nella teoria matematica della probabilità, che “PARTE” dopo la definizione dei numeri p(x)). Questo metodo
consiste nel fare un certo numero di lanci (ad esempio 120) e contare le uscite dell’1, del 2, del 3 ecc. Raccogliendo i
dati in una tabella del tipo
FACCIA DEL DADO
1
2
3
4
5
6
TOTALI
NUM. USCITE
18
22
24
18
21
17
120
PROBAB. (FRAZIONE)
PROBAB. (o/oo)
18/120 22/120 24/120 18/120 21/120 17/120 120/120=1
150.00 183.33 240.000 150.00 175.00 141.67 1000.00
otteniamo i valori di probabilità p(k), per k da 1 a 6, in forma frazionaria o millesimale (o percentuale o in altre
forme equivalenti). L’importante è notare che la somma delle singole p(k) è sempre 1.
1.2
Probabilità di un evento
In uno spazio di probabilità S è definita già inizialmente la funzione p(x) delle probabilità degli eventi ELEMENTARI, cioè
dei singoli elementi che compongono S.
Un EVENTO invece è un sottoinsieme A di S.
Ad esempio, nel lancio del dado, in cui S = {1,2,3,4,5,6}, possiamo considerare l’evento A= {1,3,5} chiamandolo “uscita di
un numero dispari”, oppure B = {4,5,6} chiamandolo “uscita di un numero della seconda metà”.
Il singolo evento elementare può sempre considerarsi come insieme. Ad esempio C = {4} può essere definito come “uscita di
un quadrato perfetto pari” mentre D = {1,4} è “l’uscita di un quadrato”.
Luigi PANARIELLO: Probabilità e statistica
pag. 6
La probabilità di un evento A è la somma delle probabilità dei singoli eventi elementari. E’ evidente che p(S)==1
mentre si pone, per ovvi motivi, p(∅
∅)=0.
Tornando all’esempio del lancio del dado:
• Caso dello spazio equiprobabile:
p(A) = p(B) = 3/6 = ½ = 0.500
p(C) = 1/6 = 0.167
p(D) = 2/6 = 1/3 = 0.333
• Caso dello spazio NON EQUIPROBABILE descritto nella tabella dell’esempio (*)
p(A) = p(1,3,5}) = p(1)+p(3)+p(5) = 18/120 + 24/120 + 21/120 = 63/120 = 52.50%
p(B) = p(={4,5,6}) = p(4) + p(5) + p(6) = 18/20 + 21/20 + 17/20 = 56/120 = 46.66%
ecc. Si noti che l’uscita di tre numeri differisce, nel caso NO N EQUIPROBABILE, a seconda di quali numeri scegliamo.
• Definizione semplificata nel caso EQUPROBABILE:
Quando ci troviamo in uno spazio equiprobabile ogni evento A consiste in un certo numero |A| di eventi elementari. Poiché
ogni evento elementare ha probabilità p=1/|A| avremo la probabilità dell’evento A data da p(A)= |A|/|S| e cioè il rapporto
fra CASI FAVOREVOLI e CASI POSSIBILI (dove intendiamo che A rappresenti tutti i casi favorevoli e S rappresenta la
raccolta di tutti i casi possibili).
• Vengono lanciati due dadi a facce equiprobabili. Qual è la probabilità P di realizzare la somma 8?
I casi possibili sono 36 = 6x6, corrispondenti a tutte le possibili coppie (1,1),(1,2)…(1,6)…(6,1)…(6,6) di uscite. I casi
favorevoli sono solo 5 e precisamente (2,6), (3,5),(4,4),(5,3),(6,2). Pertanto P = 5/36 = 13.8889%
3. PROPRIETA’ ELEMENTARI DELLA FUNZIONE DI PROBABILITA’
La funzione p(x) delle probabilità degli eventi elementari si considera quindi estesa a tutte le parti di S mediante la
definizione
p ( A) = ∑ p ( x) dove A è una parte di S (in particolare p(∅)=0, p(S)=1)
x∈A
e da questo punto di vista p(A) è una funzione che opera sulle parti A di S, cioè sugli “eventi di S”.
Le proprietà principali di tale funzione di probabilità sono:
•
0 ≤ p(A) ≤ 1, per qualunque evento A
•
p(∅
∅)=0, p(S)=1
p(A∪
∪B) = p(A) + p(B) , sempre che A e B siano disgiunti, cioè A∩B=∅, ed in tal caso i due eventi A e B si dicono
“incompatibili”
•
•
p(A∪
∪B∪
∪C…) = p(A) + p(B) + p(C) + …, sempre che A,B,C, siano a due a due reciprocamente incompa tibili ( e
quindi A,B,C,… rappresentino una partizione di S, ovvero un ricoprimento di S con parti a due a due disgiunte)
•
Se A ⊆ B allora p(A) ≤ p(B)
•
p(A-B) = p(A)-p(A∩
∩B) ovvero, equivalentemente, p(A) = p(A-B) + p(A∩
∩B)
•
p(A∪
∪B) = p(A) + p(B) – p(A∩
∩B)
•
p(A∪
∪B∪
∪C)=p(A) + p(B) + p(C) – p(A∩
∩B) – p(B∩
∩C) – p(C∩
∩A) + p(A∩
∩B∩
∩C)
1.3
Esempi di problemi risolti
1) La roulette normale è composta da 37 numeri (da 0 fino a 36) equiprobabili, di cui 18 sono rossi e 18 sono neri. Lo
zero è verde.
Probabilità di uscita del rosso: p=18/37
Probabilità di uscita nel primo terzo (da 1 a 12) : p=12/37
Probabilità di uscita di un numero positivo divisibile per 5 (5,10,15,20,25,30): p=6/37
Probabilità di uscita di due rossi consecutivi: le coppie di numeri rossi sono 18x18=324, le coppie totali sono 37x37=1’369.
Pertanto la probabilità cercata è p= 324/1’369 (in percentuale circa 23.667%, in frazione circa 100/423)
Probabilità che in due giocate escano entrambi i colori rosso e nero: Coppie rosso/nero = 324, coppie nero/rosso = 324,
coppie bicolori 324+324=648. p=648/1’369 doppia della precedente.
Probabilità che in tre giocate non esca mai un numero della prima metà (La prima metà va da 1 a 18). I casi favorevoli sono le
terne che contengono i 19 numeri, zero e altri 18 compresi tra 19 a 36. Quindi 19x19x19=6’859 sono i casi favorevoli, mentre
tutti i casi possibili sono 37x37x37=50'653. La probabilità è dunque p=6’859/50'653, circa 13.541% ovvero 100/738
Se mancasse lo zero (roulette a 36 numeri) nel caso precedente la probabilità sarebbe 1/8.
Luigi PANARIELLO: Probabilità e statistica
pag. 7
2) In un torneo a quattro squadre A,B,C,D si sa che la probabilità di vittoria di A è doppia di quella B ed il quadruplo di
quella di C. La probabilità che vinca D è del 30%. Si dicano le probabilità di vittoria di A,B,C (R. 40%, 20%, 10%)
3) Da un’urna contenente 10 palle numerate da 0 a 9 vengono estratte 3 palle in ordine cronologico (senza
reimbussolamento, considerando il caso equiprobabile) in modo da formare numeri a 3 cifre distinte (ad esempio
153, 012, ecc). Si chiede la probabilità che il numero estratto sia maggiore di 400.
I casi possibili sono evidentemente le disposizioni D10|3=10⋅9⋅8 = 720. Occorre contare dunque i numeri maggiori di 400. A
tale scopo notiamo che la prima cifra estratta deve essere necessariamente compresa fra 4 e 9 (sono 6 casi). Quindi la
seconda cifra può essere una delle rimanenti 9 e la terza una delle rimanenti 8. Abbiamo dunque 6⋅9⋅8 = 432 casi favorevoli.
La probabilità è dunque 432/720=60%
4) Da un’urna contenente 10 palle numerate da 0 a 9 vengono estratte 3 palle in ordine cronologico (con
reimbussolamento, considerando il caso equiprobabile) in modo da formare numeri a 3 cifre (ad esempio 155, 084,
ecc). Si chiede la probabilità che il numero estratto sia divisibile per 3.
Evidentemente i numeri possibili vanno da 000 fino a 999 e quindi sono 1000. Il primo è divisibile per 3. Ogni numero
divisibile per tre è seguito da due che non lo sono. Quindi da 000 fino a 998 abbiamo 333 numeri divisibili per tre e 666 non
divisibili. Aggiungendo il 999 abbiamo 334 numeri divisibili per tre per cui la probabilità è 334/1000.
5) Si calcoli la probabilità che estraendo cinque numeri del lotto da un’urna con 90 numeri equiprobabili esca un
prefissato terno.
Le cinquine che contengono il terno vincente si ottengono unendo al terno vincente tutte le possibili combinazioni degli 87
numeri restanti presi a due a due ( cioè C87|2), mentre le cinquine possibili sono C90|5 . Pertanto p= C87|2 / C90|5 = 1 / 11’748
6) Si calcoli la probabilità che giocando su cinque numeri al lotto esca un terno, con una estrazione standard di cinque
numeri, su una ruota prestabilita.
Giocando un terno prefissato la probabilità di vincita è circa 1 / 11’748 (esempio n. 3). Giocando su 5 numeri è come aver
puntato su 10 terni (quanti ne sono compresi in una cinquina). Pertanto le probabilità diventano 10/11’748 , circa 1 / 1’175 in
quanto i casi favorevoli diventano 10 volte in più. Osserviamo espressamente che se abbiamo dieci ruote NON possiamo
semplicemente moltiplicare ancora per 10 (anche se in realtà la probabilità aumenta ancora di circa 10 volte). Ed infatti se si
trattasse semplicemente di una moltiplicazione per il numero di ruote basterebbe giocare su un numero molto alto di ruote
ovvero equivalentemente di giocare più volte (più 1175) per avere la probabilità di uscita di un terno maggiore di 1.
7) Vengono distribuite 5 carte a testa a 4 giocatori di poker. Qual è la probabilità che il primo giocatore abbia un tris di
mano? E un full? E un poker? E scala reale? E colore?
Supponiamo che il mazzo di carte sia costituito dai valori A 7 8 9 10 J Q K su quattro semi (32 carte).
Sono possibili C32|5 combinazioni di 5 carte. Le combinazioni che contengono un dato tris (ad esempio un tris di J) sono C28|2
(le combinazioni di due carte prese dalle 28 che non sono J).poiché abbiamo 32 tris possibili (4 di A, 4 di K, ecc.), le
combinazioni contenenti un tris sono 32 C28|2. Facendo il rapporto fra questo numero e C32|5 otteniamo p(tris) = 108/1'798 =
1/16.6 (circa) .
I full di mano sono più rari. La disposizione deve contenere un tris ed una coppia. I tris possibili sono 32. Le coppie possibili
sono 6 per ogni valore (6 di A, 6 di K, ecc.) e quindi in tutto sono 48. Ad un dato tris possiamo aggiungere però solo le 42
coppie che non hanno lo stesso valore del tris (ad esempio ad AAA non posso aggiungere AA, ma solo KK, QQ ecc). E
quindi i full possibili sono 48⋅32=1'536. Pertanto p(full)=1’536/ C32|5 = 1/131 (circa)
Le disposizioni contenenti un poker sono 8•28 = 224 e pertanto la probabilità del poker di mano è p(poker) 224/C32|5 = 1/898
(circa)
Le scale reali sono particolari combinazioni di 5 carte delle stesso seme e precisamente {A,7,8,9,10} (scala minima),
{7,8,9,10,J}{8,9,10,J,Q}{9,10,J,Q,K} (scale medie), {10,J,Q,K,A} (scala massima). In tutto sono quindi 50 casi favorevoli e
quindi p(sc. reale) = 50/ C32|5 =1/4023 (circa)
Le combinazioni di “colore” sono 4 C 8|5 = 224 (un colore è una combinazione di 5 carte prese dalle 8 che hanno lo stesso
seme, il tutto moltiplicato per i 4 semi). Pertanto p(colore) 224/C32|5 = 1/898
8) Ina scatola di 50 lampade ve ne sono 4 difettose. Qual è la probabilità che prendendone 10 (le lampade si
considerano equiprobabili) ve ne sia una sola difettosa? e almeno una difettosa?
Vi sono C50|10 modi di prendere 10 lampade dalla scatola. Le combinazioni di 9 lampade buone sono invece C46|9. Quindi le
combinazioni di 1 lampada difettosa (4 possibilità) e di 9 lampade buone (C46|9 possibilità) sono, per il principio di
moltiplicazione, 4⋅C46|9. Quindi la probabilità cercata è p = 4⋅C46|9/ C50|10 = 0.429 circa
La probabilità che almeno una sia difettosa è complementare della probabilità che nessuna sia difettosa (che è evidentemente
un caso molto più semplice da calcolare, visto che il caso “almeno una” ci costringerebbe a considerare ed a s ommare i casi
di 1 difettosa, 2 difettose, …, 10 difettose). Le combinazioni di lampade tutte buone sono evidentemente C 40|10 e perciò la
probabilità che siano tutte buone è q = C40|10 / C50|10 = 0.08252. La probabilità complementare, che non tutte siano buone, e
quindi una almeno sia difettosa, risulta p = 1 – q = 0.91748
Luigi PANARIELLO: Probabilità e statistica
pag. 8
4. INDIPENDENZA
Si dice che gli eventi A,B,C,… sono reciprocamente indipendenti se il verificarsi di uno o più di essi non influenza il
verificarsi o meno dei restanti. Quindi il verificarsi simultaneo di A,B,C,… si può calcolare con la formula
p ( A ∩ B ∩ C.....) = p ( A) p ( B) p (C )......
ove la simultaneità è data dall’intersezione A ∩B∩C…..
Ad esempio nel lancio di una moneta, l’uscita del terzo lancio (testa o croce) non è influenzata dall’esito del primo e del
secondo lancio. Infatti in tal caso abbiamo lo spazio degli eventi S = TTT, TTC, TCT, TCC, CTT, CTC, CCT, CCC di 8
eventi elementari. Il caso “terzo lancio croce” è dato dall’evento A = { TTC, TCC, CTC, CCC} che ha probabilità 4/8=1/2
come se i precedenti lanci non fossero mai avvenuti. Il caso “secondo lancio testa” è dato invece dall’evento B = {TTT,
TTC, CTT, CTC} che ha anch’esso probabilità 1/8. Il caso “secondo lancio testa e terzo lancio croce” è rappresentato
ovviamente da A∩B = { TTC, CTC} avente probabilità (1/2)(1/2) = 1/4
Possiamo ora chiederci se l’evento B sia influenzato o meno dall’evento “nei tre lanci escono esattamente 2 teste”, C={ TTC,
TCT, CTT} che ha probabilità 3/8 di verificarsi.
Per saperlo basta confrontare p(B∩C) =p({TTC,CTC})= 2/8=1/4 con p(B)p(C)=(1/4)(3/8)=3/32 per vedere che non si tratta
di eventi indipendenti. In effetti la probabilità che “il secondo lancio sia testa e nei tre lanci esca esattamente due volte testa”
è di ¼. Mentre 3/32 rappresenta la probabilità che in DUE serie di tre lanci, nella prima serie il secondo lancio sia testa e nella
seconda serie escano esattamente due teste.
Mediante diagrammi ad albero è possibile valutare numerosi casi di calcolo probabilistico in cui si verificano sequenze
indipendenti.
Il grafico rappresenta una sfida di scacchi fra Vincenzo e
Giuseppe. Si assume che, nella singola partita, la probabilità
di vittoria di Vincenzo sia 2/3 e quella di Giuseppe di 1/3.
La sfida consiste in partite in sequenza finché uno dei due
vince due volte di seguito oppure tre volte in tutto.
Tutti i casi possibili sono riportati nel diagramma ad albero
ed ogni ramo rappresenta la probabilità (riferita alla singola
partita).
Vogliamo calcolare la probabilità che Vincenzo vinca in tre
partite.
Notiamo un solo percorso (GVV) in cui Vincenzo vince in
tre partite. La sua probabilità è (1/3)(2/3)(2/3)=4/27
La probabilità che vinca in due partite è invece
(2/3)(2/3)=4/9.
La probabilità che Vincenzo vinca in meno di quattro partite è quindi 4/9+4/27=16/27 (superiore al 50%)
Le probabilità di vittoria di vittoria della sfida per Giuseppe si ottengono sommando le probabilità dei 5 percorsi che
terminano con G, e sono meno di 1/3:
p = (1/3)(1/3)(2/3)(1/3)(2/3) + (2/3)(1/3)(1/3) + (1/3)(1/3)(2/3)(1/3) + (1/3)(2/3)(1/3)(2/3)(1/3) + (1/3)(1/3) =
= 4/243 + 2/27 + 2/81 + 4/243 + 1/9 = (4 + 18 + 6 + 4 + 27)/243 = 59/243 = 0.2428
5. PROBABILITA’ CONDIZIONATA
Spesso occorre definire la probabilità di un evento A sapendo che si è già verificato l’evento T (avente probabilità non nulla
di verificarsi) e che A e B non sono indipendenti. Tale probabilità viene chiamata “probabilità condizionata” di A dato T ed
indicata con p(A|T)
La probabilità viene definita con la formula
p( A | T ) =
p( A ∩ T )
p (T )
che ha il seguente significato:
Si ridefinisce lo spazio degli eventi, limitandolo all’insieme T ed
assegnandogli probabilità condizionata 1, cioè p(T|T)=1.
L’evento A condizionato da T è nient’altro che A ∩T e quindi si misura la
sua probabilità in T facendo il rapporto fra la probabilità in S e la probabilità
di T in S.
Luigi PANARIELLO: Probabilità e statistica
pag. 9
In particolare se si tratta di uno spazio equiprobabile basta considerare i rapporti numerici, avendosi
| A ∩T |
p( A ∩ T )
| A∩T |
|S|
p( A | T ) =
=
=
(caso di spazio equiprobabile)
T
|
|
p (T )
|T |
|S|
Inoltre si osserva che la probabilità condizionata ci consente di esprimere un importante “Teorema di moltiplicazione”:
p ( A ∩ B) = p ( A) p ( B | A)
Nel caso si abbiano tre eventi A,B,C, potendo scrivere:
p(C | B ∩ A) =
p( A ∩ B ∩ C ) p( A ∩ B ∩ C )
avremo anche
=
p( B ∩ A)
p( A) p( B | A)
p ( A ∩ B ∩ C ) = p ( A) p ( B | A) p (C | A ∩ B)
che potrebbe essere sviluppato al caso di n eventi.
Esso afferma che la probabilità dell’evento congiunto di più eventi è data dal prodotto della probabilità del primo, per la
probabilità del secondo condizionata dal primo, per la probabilità del terzo condizionata dalla congiunzione del primo e del
secondo ecc.
•
Esempio 1: Un’urna contiene 10 biglie numerate da 1 a 10 con equiprobabilità nell’estrazione. Se ne estraggono tre.
Si vuole la probabilità che siano tre pari.
La probabilità che il primo sia pari è 5/10. La probabilità che il secondo sia pari dopo che il primo è già stato pari è 4/9. La
probabilità che il terzo sia pari dopo che già il primo ed il secondo sono stati pari è 3/8. La probabilità cercata, per il teorema
di moltiplicazione è (5/10)(4/9)(3/8) = 1/12.
Lo stesso risultato si ottiene considerando le C10|3 combinazioni possibili e le C5|3 combinazioni favorevoli. p= C5|3 /C10|3
•
Esempio 2: Viene lanciato un dado truccato in maniera che i numeri piccoli (1-2-3) abbiano metà probabilità di
uscita di quelli grandi (4-5-6). Se esce il numero k viene lanciata k volte una moneta con testa e croce
equiprobabile. Si vuole sapere la probabilità che testa esca due volte.
La probabilità di uscita di un numero piccolo (1-2-3) con il dado è di 1/9 mentre per i numeri grandi è 2/9. Si noterà che la
somma 3(1/9)+3(2/9)=9/9=1. La probabilità p che esca due volte testa in k lanci dipende da k:
k=1 p=0; k=2 p=1/4; k=3 p=3/8; k=4 p=6/16; k=5 p=10/32; k=6 p=15/64
Ognuna delle sei probabilità è condizionata dall’uscit a di k e quindi va moltiplicata per 1/9 (k=1,2,3) oppure per 2/9
(k=4,5,6). Le sei probabilità ottenute potranno poi sommarsi in quanto valori distinti di k sono eventi incompatibili.
Si ha quindi P=0(1/9)+(1/4)(1/9)+(3/8)(1/9)+(6/16)(2/9)+(10/32)(2/9)+(15/64)(2/9)=158/576 = 0.27430
•
Esempio 3: La formula
p ( A ∩ B) = p ( A) p ( B | A) si riduce a p ( A ∩ B ) = p ( A) p ( B) ogniqualvolta risulta
p ( B ) = p ( B | A) . Quest’ultima ha il significato di “indipendenza” di B rispetto ad A: l’evento A può verificarsi o
meno senza influenzare la probabilità di B. Si riottiene in tal modo la formula della probabilità di eventi congiunti
indipendenti
6. IL TEOREMA DI BAYES
In forma semplificata il Teorema di Bayes (detto anche “delle probabilità delle cause”) si può ottener e dalla legge
commutativa dell’intersezione per cui
p ( A ∩ B ) = p ( A) p ( B | A) = p ( B) p ( A | B) = p ( B ∩ A)
Infatti da essa possiamo ricavare
p( A | B) =
p ( A) p ( B | A)
p( B)
che rappresenta la formula cercata.
•
Esempio 1: Abbiamo due macchine, (a) che produce 400 pezzi al giorno di cui in media 8 difettosi, (b) che produce
600 pezzi al giorno di cui in media 6 difettosi. Da un campione di 100 pezzi se ne estrae uno a caso ed esce
difettoso. Si vuole conoscere la probabilità che la causa del difetto sia stata la prima macchina.
Consideriamo gli eventi: A=”il pezzo è stato prodotto dalla macchina(a)” con probabilità p(A)=600/1000
B=”il pezzo è difettoso” con probabilità p(B)=14/1000
B|A =”il pezzo è difettoso e sappiamo che è stato prodotto da (a)” con probabilità p(B|A)=6/600
La probabilità cercata (cioè di A|B=”il pezzo è stato prodotto da (a) e sappiamo che è difettoso”) verrà fornita dal teorema di
Bayes e ci dà: p(A|B)=(600/1000)(6/600)(1000/14)=6/14
Luigi PANARIELLO: Probabilità e statistica
pag. 10
•
Esempio 2: In una scuola il rapporto numerico maschi/femmine è di 4 a 9. Il 12% delle femmine e il 30% dei
maschi supera l’altezza di 170 cm. Si sceglie a caso un allievo e la sua altezza supera i 170 cm. Si vuole sapere la
probabilità che sia maschio.
Consideriamo gli eventi: A=”l’allievo è maschio” con probabilità p(A)=4/13=0.30769
B=”l’alli evo supera 180 cm” con probabilità p(B)=(12/100)(9/13)+(30/100)(4/13) = 0.17538 (fare
diagramma ad albero)
B|A =”l’allievo supera 180 cm e si sa che è maschio” con probabilità p(B|A)=30/100=0.30000
La probabilità cercata (cioè A|B=”l’allievo è maschio e si sa che supera 180 cm”) ci viene data dalla formula di Bayes che
fornisce p(A|B)=(0.30000)(0.30769)/(0.17538)=0.52633 maggiore del 50%.
7. LE MEDIE NUMERICHE
Sia dati n numeri x1,x2,….,x n.
Si definisce “ media aritmetica” degli n numeri quel numero x m che sostituito al posto degli xi lascia inalterata la loro
somma. Naturalmente risulta
xm =
x1 + ...+ xn
n
che deriva da xm+…+x m=x1+…+x n ovvero nxm= x1+…+x n
Si definisce “ media geometrica” degli n numeri quel numero x g che sostituito al posto degli xi lascia inalterato il loro
prodotto.
Quindi xg….x g= x1…x n ovvero (xg)n= x1…x n, da cui discende
xg = n x1x2 ⋅⋅⋅ xn
Se i numeri xi non sono considerati una sola volta, nel senso che p1 sono x1,….,p n sono xn, le medie, pur rimanendo dello
stesso significato, cambiano formula potendo scrivere
xm =
p1x1 +...+ pn xn
p1 +...+ pn
xg = p1+...+pn x1p1 ⋅⋅⋅ xnpn
i numeri pi sono chiamati “pesi” dei numeri x i e le media sono chiamate “ medie pesate”.
Posto p=p1+….+p n (peso totale dei numeri), il numero xi ha “probabilità di usc ita” f i= pi/p. Il numero fi (non superiore ad 1) è
detto “frequenza relativa” del numero x i.
Per la media aritmetica si ha l’importante formula
xm =
p1 x1 + ... + p n x n
p x + ... + p n x n
p
p
= 1 1
= 1 x1 + ... + n x n = f1 x1 + ... + f n x n
p1 + ... + p n
p
p
p
Naturalmente se i pesi sono tutti uguali (in particolare 1) torniamo alla formula della media non pesata con fi = (1/n)
Si definisce inoltre “ media quadratica” dei numeri x 1,x2,….,x n, il numero xq sostituito al posto degli n numeri non cambia la
somma dei quadrati. Pertanto avendosi
xq2 + ... + xq2 = x12 + ... + xn2 , ovvero nxq2 = x12 + ... + xn2 , potremo scrivere la
formula della media quadratica
x12 + ...+ xn2
xq =
n
Se ai numeri xi attribuiamo i “pesi” p i ovvero le frequenze fi possiamo calcolare la media quadratica con le formule
xq =
1.4
p1 x12 + ... + p n x n2
=
p
f 1 x12 + ... + f n x n2
SCARTI
Data un valore xo calcolato a partire dai numeri x1,x2,….,x n, si definisce “ scarto di xk rispetto ad xo” o semplicemente
“ scarto k-esimo” la differenza (presa algebricamente con segno) ∆xk=xk-xo.
Lo scarto quadratico medio è nullo se (e solo se) xo=xm, cioè se è la media aritmetica degli n numeri. Infatti ∆x1+…+ ∆xn =
=(x1-xo)+…+ (x n-xo)=(x1+…+ x n) –(xo+…+ x o)=nxm-nxo= n(xm-xo) e l’ultima espressione è zero se e solo se x m=xo
Luigi PANARIELLO: Probabilità e statistica
pag. 11
Lo scarto quadratico medio (cioè la media quadratica degli scarti) si annulla solo se gli scarti sono tutti nulli e cioè se gli n
numeri sono tutti uguali ad xo.
Normalmente lo scarto quadratico medio si valuta rispetto alla media aritmetica dei numeri. Lo scarto quadratico medio
rappresenta la “dispersione” dei numeri intorno al loro valore med io. In particolare si può dimostrare che la media aritmetica
rende “MINIMO” lo scarto quadratico medio, che indicheremo in tal caso con σ.
Infatti consideriamo il numero xo = xm+h, essendo h la differenza fra il numero xo e la media aritmetica xm, e calcoliamo lo
scarto quadratico medio rispetto ad xo, che indicheremo con ∆xq. Per verificare la questione del minimo potremo
naturalmente considerare il quadrato dello scarto quadratico medio per evitare calcoli sotto radice:
∆xq2 =
1 n
1 n
1 n
( xi − xo ) 2 = ∑[( xi − xm ) − h]2 = ∑[( xi − xm ) 2 + h 2 − 2h( xi − xm )] =
∑
n i =1
n i =1
n i =1
1 n
 1

1 n
=  ∑ ( xi − x m ) 2  + h 2 + 2 h  ∑ ( xi − x m ) 
n  i =1
 n i =1
 n

Nell’ultimo me4mbro riconosciamo la prima sommatoria che rappresenta lo scarto quadratico medio rispetto alla media
aritmetica, cioè σ2, e la seconda sommatoria che è la media aritmetica degli scarti rispetto alla media aritmetica, che è zero.
Pertanto il minimo si otterrà quando h2=0 e quindi per xo=xm
n
Il quadrato dello scarto quadratico medio
σ 2 = ∑ ( xi − xm ) 2 si chiama “varianza dei numeri xi”
i =1
Essa può essere calcolata anche come differenza fra il valore quadratico medio al quadrato e la media aritmetica al quadrato,
infatti
σ2 =
n
1 n
1 n
1 n
1 n
1 n
1 n
2
1 n
( xi − xm ) 2 = ∑ xi2 + ∑ xm2 − ∑ 2 xm xi = ∑ xi2 + ∑ xm2 − xm ∑ xi = ∑ xi2 + xm2 − 2 xm2
∑
n i =1
n i=1
n i =1
n i =1
n i =1
n i =1
n i =1
n i =1
σ2 =
1n 2 2
2
xi − xm = Xq − xm2
∑
n i=1
dove Xq è il valore quadratico medio degli n numeri e xm la media aritmetica.
In conclusione, si definisce lo scarto quadratico medio (rispetto alla media):
n
σ=
∑(x − x )
i
i=1
m
2
2
= Xq − xm2
n
Nel caso in cui i numeri xi fossero affetti da pesi pi (e frequenze fi), lo scarto quadratico medio diventa naturalmente
n
σ=
∑p (x − x )
i=1
i
i
p
m
2
=
n
∑f (x − x )
i=1
i
i
m
2
2
= Xq − xm2
dove p è il peso totale, dove Xq è il valore quadratico medio pesato degli n numeri e xm la media aritmetica pesata.
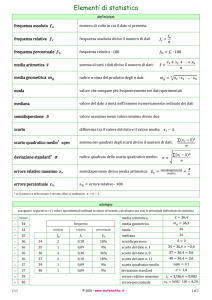
8. MODA E MEDIANA
Siano dati n valori numerici distinti x1,x2,…,x n che supponiamo di aver già ordinato: x1 < x2 <…< x n che in una serie di p
prove si sono presentati rispettivamente p1 volte, ….,p n volte, cioè con frequenze fi = pi/p.
Un valore di maggior frequenza, cioè con fi non inferiore alle altre, si chiama “ moda”.
Richiama invece “ mediana” un valore x c che bipartisce le p prove in modo che metà dei numeri sia non superiore a xc e
l’altra metà sia non inferiore a x c.
Consideriamo ad esempio la tabella:
Luigi PANARIELLO: Probabilità e statistica
pag. 12
X
P
10
2
12
6
14
7
16
3
18
3
20
1
F
C
2/22
2
6/22
8
7/22
15
3/22
18
3/22
21
1/22
22
FC
2/22
8/22
15/22
18/22
21/22
22/22
Nella prima riga sono riportati i numeri x1,x2,…,x 6, nella seconda i “pesi” ovvero il numero di uscit e (la frequenza assoluta),
nella terza la frequenza (equivalente ad una probabilità di uscita)
Nella quarta riga è riportata la “frequenza (assoluta) cumulata”, cioè il numero di prove in cui il numero non è stato
superato.
Ad esempio nella quarta colonna si legge che il numero 16 è uscito 4 volte, ovvero 4 volte su 22, che per 18 volte il 16 non è
stato superato (sono usciti 10,12,…16), che questo è avvenuto 18 volte su 22.
Naturalmente il 20, valore massimo dei numeri, ha frequenza cumulata massima, cioè 22/22.
La “moda” è 14 (valore più frequente).
La mediana è ancora 14, infatti nelle 22 prove abbiamo che per 11 volte sono usciti i numeri da 10 a 14, e per altre 11 volte
sono usciti numeri da 14 a 20
Calcoliamo invece la media aritmetica:
X
m
=
2
6
7
3
3
1
312
= 14 . 18
10 +
12 +
14 +
16 +
18 +
20 =
22
22
22
22
22
22
22
Lo scarto quadratico medio è
σ =
2
6
7
1
(14 . 18 − 10 ) 2 +
(14 . 18 − 12 ) 2 +
(14 . 18 − 14 ) 2 + .... +
(14 . 18 − 20 ) 2 = 2 . 62
22
22
22
22
Come esercizio provare anche che
2
2
σ = xq − xm (dove xq rappresenta il valor quadratico medio pesato delle xi)
9. VARIABILI CASUALI
Supponiamo che nello spazio degli eventi S (sempre limitandoci al caso finito) sia assegnata una “variabile casuale (o
aleatoria) X”, ovvero per ciascun evento elementare a∈S sia dato un valore numerico reale X=X(a) (dipendente da a)
Si può definire la probabilità P(X=xo) che la variabile assuma il valore xo, considerando tutti gli a∈S per cui p(a)= xo, e
sommando tutte le loro probabilità p(a).
In modo analogo si definiscono le probabilità P(xo ≤ X ≤ x1) che la variabile X sia compresa fra xo ed x1, P(X ≤ x1) che non
superi x1, ecc.
Si definisce “valore medio di X (su S)” (oppure valore atteso, valore sperato ecc.) la media ponderata (prendendo la
probabilità come peso o come frequenza) dei valori possibili di X, ovvero
µ( X ) = ∑ p(a) X (a)
a∈S
dove p(a) è la probabilità dell’evento elementare A.
In modo analogo si definiscono la varianza VAR(X), lo scarto quadratico medio σ, il valore quadratico medio Xq, la
moda, la mediana ecc. In particolare il valore mediano Xc deve bipartire S, in modo P(X<Xc) ≤ ½ e P(X>Xc) ≤ ½
Se il valore X rappresenta il “prem io” in un gioco d’azzardo, il valore sperato µ(X) rappresenta la speranza di premio. In tal
caso il gioco si considera “ equo” se il valore sperato è pari alla “puntata” del giocatore, cioè alla tassa di ingresso nel gioco.
Ad esempio consideriamo il gioco della roulette (37 numeri equiprobabili, se si punta sul numero giusto si vince 36 volte la
posta). Detta P la posta sul numero N (fra 0 e 36) , vinceremo 36T in un caso e 0T=0 in 36 casi. Le probabilità sono
rispettivamente 1/37 e 36/37. La speranza è 36T(1/37)+0(36/37)=(36/37)T < T. Quindi il gioco non è equo, in quanto la
vincita media è inferiore alla puntata.
•
Esempio 1: Su un bersaglio circolare di raggio 3 vengono segnati due cerchi concentrici di raggi 1 e 2. Un tiratore
ha probabilità 72% di colpire il bersaglio e nell’ambito del bersaglio le probabilità sono proporzionali alle aree. I
punti sono segnati nel grafico. Si chiedono: i punti sperati (valore medio in punti) , la varianza, lo scarto quadratico
medio, la moda, la mediana.
Le aree dei cerchi sono proporzionali ai quadrati dei raggi (12=1; 22=4; 32=9), le aree dei punti sono dunque proporzionali (da
dentro verso fuori) a 1, 3, 5 (la somma è 9). Le probabilità devono ripartirsi il totale 72% di colpire il bersaglio e pertanto
sono (da dentro verso fuori) 8%, 24%, 40%
Luigi PANARIELLO: Probabilità e statistica
pag. 13
Gli eventi e i relativi valori di X (variabile casuale) sono:
a = fuori bersaglio (X=0); probabilità p(a)=28% (= 100%-72%)
b = colpisce zona centrale (X=20); p(b)=8%
c = colpisce zona intermedia (X=10); p(c)=24%
d = colpisce zona periferica (X=5); p(d)=40%
Il valore sperato dei punti è:
µ(X)= 0.28x0 + 0.08x20 + 0.24x10 + 0.40x5 = 6
Il valore quadratico medio è:
Xq = 0(0.28)20 + 20(0.08)2 +10(0.24)2 + 5(0.40)2 = 66
La varianza :
Var(X) = Xq2-µ2(X ) = 66-36 = 30
Lo scarto quadratico medio :
σ= Var ( X ) = 5.48
La moda è 5 punti, poiché il caso d è il più frequente. La mediana Xc è 5. Infatti P(X<5) = p(a) = 28% ≤ ½
p(X>5)=p(b)+p(c)=32% ≤ ½
e
•
Esempio 2: Un cassetto contiene 10 banconote di cui 5 false. Il cassiere ne estrae una alla volta e ne verifica la
validità. Si chiede il valore atteso di banconote estratte prima di trovarne una falsa.
Detto X il numero di banconote estratte PRIMA di quella falsa, le probabilità sono:
P(X=0) è la probabilità che la prima banconota sia falsa è 5/10
P(X=1) è probabilità che la seconda sia falsa e che la prima è buona è (5/10)(5/9)
P(X=2) è la probabilità che la terza sia falsa sapendo che le precedenti sono buone è (5/10)(4/9)(5/8)
P(X=3) è la probabilità che la quarta sia falsa sapendo che le precedenti sono buone è (5/10)(4/9)(3/8)(5/7)
P(X=4) è probabilità che la quinta sia falsa sapendo che le precedenti sono buone è (5/10)(4/9)(3/8)(2/7)(5/6)
P(X=5) è probabilità che la sesta sia falsa sapendo che le precedenti sono buone è (5/10)(4/9)(3/8)(2/7)(1/6)(5/5)
µ(X ) = 0
5
5 5
5 4 5
5 4 3 5
5 4 3 2 5
5 4 3 2 1 5
5
+1
+2
+3
+4
+5
=
10
10 9
10 9 8
10 9 8 7
10 9 8 7 6
10 9 8 7 6 5
6
Provare per esercizio che
5
∑
i =1
P ( X = i) =
5
5 5
5 4 5
5 4 3 5
5 4 3 2 5
5 4 3 2 1 5
+
+
+
+
+
=1
10 10 9 10 9 8 10 9 8 7 10 9 8 7 6 10 9 8 7 6 5
L’esempio precedente può trasformarsi in gioco considerando un mazzo di 10 carte di cui 5 di cuori e 5 di picche.
Si estraggono le carte fino a che non ne esce una di picche. Si prendono 600 $ dal “banco” per ogni carta rossa uscita prima di
quella di picche. La speranza di vittoria è 600x5/6 = 500 $. Pertanto la puntata “equa” è di 500$. Si può perdere tutto (se esce
picche di prima mano), si possono vincere100$ se esce picche di seconda mano. Ma se esce picche di sesta mano si prendono
3000$ di cui 2500 $ di vincita, ma la cosa è molto improbabile (capita in media una volta ogni 252 giocate).
Se la puntata viene portata a 600$ il gioco diventa favorevole al “banco” che guadagna in media 100$ a puntata.
10. SISTEMI DI DUE VARIABILI CASUALI
Siano X, Y due variabili casuali entrambe su uno spazio di probabilità finito S.
La X possa assumere gli r valori x1,…,x r con le probabilità P(X= x1)=px1,…, P(X= x r)=pxr
La Y possa assumere gli s valori x1,…,x s con le probabilità P(Y= y1)=py1,…, P(Y= y r)=pys
La probabilità che X, Y possano assumere simultaneamente il valori X = xi e Y = yj verrà indicata con pij
Se (e solo se) le variabili X ed Y sono indipendenti avremo pij =pxipxj ovvero P(X=xi e Y=yj) = P(X=xi )P(Y=yj)
Luigi PANARIELLO: Probabilità e statistica
•
pag. 14
Esempio 1: Sia S lo spazio di probabilità associato al lancio di due monete con testa (T ) e croce (C) equiprobabili.
Lo spazio degli eventi è costituito da (TT),(TC),(CT),(CC). Consideriamo come variabile X il numero di croci che
esce nel lancio. Quindi i valori assunti da X saranno 2 (con prob. ¼), 1 (con prob. ½) e 0 (con prob. ¼).
Consideriamo inoltre la variabile Y che rappresenta 0 se non esce croce (prob. ¼) oppure 1 se esce qualche croce
(prob. ¾). Costruiremo la tabella (X, Y, pi,j)
.
X
Y
0
1
2
0-1-2
0
1/4
0
0
1/4
1
0
1/2
1/4
¾
0-1
1/4
1/2
1/4
1
Nell’ultima colonna sono riportate le probabilità p y, nell’ultima riga sono riportate le probabilità p x . Le probabilità singole pij
sono calcolate mediante i rapporti fra casi favorevoli e casi possibili. Si noti che p(X=0 e Y=0) = ¼ non coincide con
P(X=0)p(Y=0)= 1/16. Pertanto le due variabili X ed Y non sono indipendenti.
•
Esempio 2: Consideriamo invece due dadi equiprobabili, uno rosso ed uno bianco, e si dicano X il numero uscito dal
dado rosso ed Y invece indichi 1 se il dado rosso da più di 4 e zero in caso contrario
X
1
2
3
4
5
6
Y
0
1/9
1/9
1/9
1/9
1/9
1/9
2/3
1
1/18
1/18
1/18
1/18
1/18
1/18
1/3
1/6
1/6
1/6
1/6
1/6
1/6
1
Si nota che P(X=i e Y=j) = P(X=i)P(Y=j) per i=1,…,6 e j=0,1. Quindi le due variabili sono indipendenti.
Dagli esempi precedenti, ovvero con un semplice ragionamento, possiamo anche dedurre che:
∑p
i =1...r
ij
= p yj ,
∑p
j =1...s
ij
∑p
= p xi ,
i =1...r
j =1...s
=1
ij
Per le due variabili casuali X ed Y si definisce la somma X+Y che assume tutti i valori xi+yj con le probabilità pij, il prodotto
XY che assume i valori xiyj con le probabilità pij. Più in generale si definisce qualunque funzione f(X,Y) delle due variabili
assumendo che possa valere f(xi,yj) con probabilità pij.
Si definisce poi la “ covarianza” cov(X,Y) delle due variabili ponendo cov(X,Y) =
∑(x
i =1...r
j =1...s
i
− µ x )( y j − µ y ) pij , essendo µx
e µy i valori medi di X ed Y
Nell’esempio 1 la covarianza è 3/16. Nell’esempio 2 la covarianza è 0.
La covarianza è zero ogniqualvolta le due variabili sono indipendenti. Ed infatti in tal caso si ha:
∑(x
i =1...r
j =1...s
i
− µ x )( y j − µ y ) pij =
∑xp ∑
i =1...r
i
i
j =1...s
∑ (x
i =1...r
j =1... s
y j p j − µx
i
− µ x )( y j − µ y ) pi p j =
∑y
j =1...s
j
pj
∑(x y
i =1...r
j =1...s
i
∑p −µ ∑ x p ∑p
i =1...r
i
y
i =1...r
i
i
j =1...s
j
j
= µxµy − µxµy − µxµy + µxµ y = 0
− µ x y j − µ y xi + µ x µ y ) p i p j =
+ µxµ y
∑ p ∑p
i =1...r
i
j =1...s
j
=
Luigi PANARIELLO: Probabilità e statistica
pag. 15
Quando due variabili hanno covarianza zero si dicono “non correlate”. Quindi due variabili indipendenti sono sempre no n
correlate. Il teorema inverso non vale, quindi due variabili dipendenti (non indipendenti) potrebbero risultare
probabilisticamente non correlate.
La correlazione può essere positiva (all’aumentare di una probabilmente aumenta l’altra e viceversa) o nega tiva
(all’aumentare di una l’altra probabilmente diminuisce) a seconda che cov(X,Y)>0 o cov(X,Y)<0.
Nell’esempio 1 la covarianza positiva 3/16 mostra che X ed Y sono positivamente correlate: l’aumento di Y da 0 ad 1
(l’uscita di una croce) aumenta il valor e probabile di X (il numero di croci uscito).
Date due variabili casuali X,Y si ha, per la media e la varianza:
µ( X + Y ) =
∑ (x
i =1...r
j =1...s
Var(X +Y) = σ 2X +Y =
=
∑ (x
i =1...r
i
i
+ y j ) pij =
∑(x − µ
i=1...r
j =1...s
− µ x ) 2 p Xi +
i
∑( y
j =1...s
∑ x ∑p
i =1...r
i
j =1... s
ij
+
∑
j =1...s
yj
∑p
i =1...r
ij
=
∑x p
i =1...r
Xi
+
∑y
j =1... s
j
pYj = µ ( X ) + µ (Y )
x
+ y j − µy )2 pij = ∑ (xi − µx )2
j
− µ y ) 2 p yj + 2 ∑ ( xi − µ x )( y j − µ y ) pij = Var ( X ) + Var ( y ) + 2Cov( X , Y )
i=1...r
∑p + ∑ ( y
i
j =1...s
ij
j =1...s
j
− µy )2 ∑pij +2 ∑(xi − µx )(y j − µy ) pij =
i=1...r
i=1...r
j =1...s
i =1...r
j =1...s
In particolare se X, Y non sono correlate (in particolare se sono indipendenti):
Var ( X + Y ) = Var ( X ) + Var ( y )
Si possono considerare più di due variabili casuali X,Y, Z,…
Si può dimostrare che
µ ( X + Y + Z + ...) = µ ( X ) + µ (Y ) + µ ( Z ) + ... e che, se sono reciprocamente indipendenti:
Var ( X + Y + Z + ...) = Var ( X ) + Var (Y ) + Var ( Z ) + ...
11. LA LEGGE DEI GRANDI NUMERI
Consideriamo una variabile casuale X sullo spazio di probabilità S, avente n eventi elementari di probabilità p(1),….,p(n),
n
con valore medio µ. La varianza Var(X) è data da
σ 2 = ∑ p (i)( Xi −µ ) 2 . Sia θ un numero positivo scelto a piacere. Se
i =1
nella formula della varianza (che è una sommatoria di numeri mai negativi) sostituiamo i termini (Xi-µ)2 che sono più piccoli
di θ2 con zero e sostituiamo quelli più grandi con θ2, alla fine troveremo una sommatoria che certamente non è superiore a
quella di partenza. Pertanto potremo scrivere:
n
σ 2 = ∑ p (i )( Xi −µ ) 2 ≥ ∑ p (i)θ 2 = θ 2 ∑ p (i ) = θ 2 P(( Xi − µ ) 2 ≥ θ 2 )
i =1
*
*
dove il simbolo (*) sotto alla sommatoria significa che essa è estesa solo ai termini che danno (Xi-µ)2 ≥ θ2. Mettendo θ2 in
evidenza risulta la sommatoria delle probabilità degli eventi in cui (Xi-µ)2 ≥ θ2, e quindi la probabilità complessiva che
indichiamo con P((Xi-µ)2 ≥ θ2).
D’altra parte (X i-µ)2 ≥ θ2 equivale perfettamente a |Xi-µ| ≥ θ e quindi P((Xi-µ)2 ≥ θ2) = P(|Xi-µ| ≥ θ). Avremo dunque:
σ2
P(| X − µ |≥ θ ) ≤ 2
θ
(disuguaglianza di Tchebychef:)
Se poniamo θ = mσ avremo una formula più più significativa:
P(| X − µ |≥ mσ ) ≤
σ2
1
= 2
2 2
mσ
m
Ad esempio la probabilità che il valore della variabile casuale X si distacchi dalla media di un valore di almeno 3σ è inferiore
ad 1/9.
Supponiamo ora di avere una successione variabili casuali indipendenti X1, X2, ….,Xk,… sullo spazio degli eventi S, con la
condizione che tutte abbiano lo stesso valore medio µ e lo stesso scarto quadratico medio σ (e quindi la stessa varianza). Si
σ = σ1 = … = σk = ….
abbia cioè µ = µ1 = … = µk = … e
Si può allora considerare la cosiddetta “ media campionaria” delle prime k variabili .
Il valore sperato della media campionaria sarà ancora µ, infatti:
Luigi PANARIELLO: Probabilità e statistica
µ (M k ) = µ (
pag. 16
X 1 + ... + X k
µ ( X 1 ) + ... + µ ( X k ) µ + ... + µ kµ
=
=
=µ
)=
k
k
k
k
Per la varianza, trattandosi di variabili indipendenti, risulta:
Var ( M ) = Var (
X 1 + ... + X k
σ2
1
1
1
2
=
+
+
=
+
+
=
σ
=
Var ( X 1 ... X k )
k
)
[Var ( X 1 ) ... Var ( X k )]
k
k2
k2
k2
k
Quindi la sequenza X1,…,X k ha, come media campionaria, una varianza inferiore alle singole variabili Xi.
Se applichiamo la formula di Tchebychef alla media campionaria Mk, riferita alle prime k variabili, e teniamo presente che la
varianza è σ2/k avremo:
σ2
per cui, pssando al limite per k → ∞ si ha
kθ 2
lim P(| M k − µ |≥ θ ) = 0 ovvero, considerando l’evento contrario, lim P(| M k − µ |< θ ) = 1
P(| M k − µ |≥ θ ) ≤
k →∞
k →∞
Il teorema dimostrato è noto come “Legge (debole) dei grandi numeri”. L’attributo “debole” deriva dal modo in cui è
congegnato il limite.
Cerchiamo di ricostruirne il significato probabilistico.
Con S abbiamo indicato uno “spazio finito di probabilità” e con X 1,…,X k,…. una successione di variabili casuali su S,
indipendenti reciprocamente, con lo stesso valore medio µ, la stessa varianza Var(Xi)=σ2, e quindi con lo stesso scarto
quadratico medio σ.
In pratica possiamo pensare di ripetere un esperimento, sempre con le stesse modalità, per un numero (k) di volte.
Se non cambiamo modalità resteranno costanti per ciascun esperimento il valore sperato µ e lo scarto quadratico medio σ.
Sia X la variabile casuale che si vuole valutare. Ogni esperimento compiuto fornisce un “valore sperimentale” di X. I k
esperimenti forniscono i valori x1,…,x k e la media campionaria assume il valore Mk = mk = (x1+…+x k)/k
Fissato un numero θ positivo, piccolo a piacere, possiamo calcolare la probabilità che il numero mk differisca poco da µ (cioè
che la media campionaria dopo k esperimenti differisca poco dal valore sperato µ): il poco è dato dal numero θ.
La legge dei grandi numeri afferma che il limite di questa probabilità è 1 e che quindi per grandi numeri k siamo quasi certi
che la differenza fra il valore della media campionaria ed il valore sperato è piccolo. Tuttavia la casualità insita nel 1°
esperimento è la stessa del k° esperimento! Quindi secondo la legge dei grandi numeri può capitare che il valore uscito xk nel
k° esperimento sia uno dei più improbabili.
12. DISTRIBUZIONE BINOMIALE (di Bernoulli)
Consideriamo prove ripetute ed indipendenti di un esperimento con due esiti, uno chiameremo “successo” di ‘probabilità p e
l’altro di “insuccesso” di probabilità q=1 -p. Considerando una variabile casuale X, assumeremo X=1 in caso di successo e
X=0 in caso di insuccesso.
La probabilità di ottenere esattamente k successi in n prove (con 0 ≤ k ≤ n) è data da
n
B ( k | n ) =   p k q n − k .
k 
Infatti il caso particolare in cui a k successi iniziali seguono n-k insuccessi ha probabilità (data l’indipendenza) p kqn-k.
Tutti gli altri casi si ottengono considerando il loro numero, che equivale al numero di combinazioni di ordine n e classe k,
che sono Cn|k =
 n
  , da cui la formula
k 
Se sommiamo tutti i valori di B(k|n) da k=0 a k=n otterremo naturalmente 1 ed infatti
 n  k n−k
  p q = ( p + q ) n = 1
k = 0... n  k 
∑ B (k | n) = ∑
k = 0... n
Il precedente calcolo spiega il motiva del nome “distribuzione binomiali” alla distribuzione di probabilità B(k|n)
Luigi PANARIELLO: Probabilità e statistica
•
pag. 17
Esercizio: Pelè segna i rigori con la probabilità p=0.85 (dell’85%). Calcolare la probabilità che tirando 5 volte segni
3 gol, oppure 4 gol, oppure almeno un gol.
La prima probabilità è B(3|5)=10 (0.85)3 (0.15)2 = 0.1382 = 13.82%
La seconda è B(4|5)=5 (0.85)4 (0.15)1 = 0.3915 = 39.15%
La terza è la complementare di B(0|5) e cioè 1-B(0|5)=1-(0.15)5=99.999 = 99.99%
Calcoliamo il valor medio (sperato) di successi e la varianza dopo n prove (dove X =0,1 è la variabile casuale e pk=B(k|n)):
µ( X ) =
n
∑ kp = ∑ k  k  p
i =1...n
k
i =1...n
k
 n − 1  k −1 n−k
 n − 1  h n−1−k
q n−k = ∑ np
=np ( p + q ) n−1 = np
 p q =np ∑ 
p q
 k −1 
i =1...n
i = 0...( n −1)  h 
•
Esempio 1: Lanciando il dado equiprobabile abbiamo probabilità 1/6 che esca “6”. Lanciando il dado 600 volte ci si
aspetta che il 6 esca np volte ovvero 600(1/6)=100 volte.
•
Esempio 2: Se Pelè tira 100 rigori (p=85% di successo), qual è il numero sperato s di gol ?