Esempio prova d`esame

Corso di laurea in
MANAGEMENT DELL'INFORMAZIONE E DELLA COMUNICAZIONE AZIENDALE
a.a. 2014-2015
Statistica per l’Azienda
Pre-appello 20-05-2015
Firma_______________________________ CFU______
A
Cognome_______________________Nome______________________MTR___________Serale Sì
No
Esercizio 1
Per la valutazione degli agenti di commercio di una multinazionale presente sul territorio Italiano, l’ufficio
personale ha deciso di raccogliere le seguenti informazioni sui dipendenti della filiale di Torino: “numero di
nuovi contratti portati a termine” (Y) e il “numero di nuovi clienti contattati” (X).
Nome
X
Y
Paolo
10
8
Andrea
15
10
Anna
15
8
Luca
10
10
Alessandra
20
15
Per quanto riguarda il fenomeno X:
a) Costruire la distribuzione di frequenza, indicando sia le frequenze assolute che quelle relative
xi
Freq. assolute
Freq. relative
b) Fornire i seguenti grafici
Grafico della distribuzione di frequenza
Grafico della funzione di ripartizione
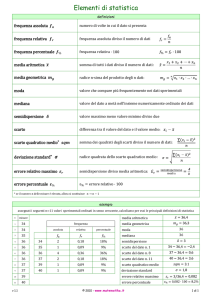
c) Se possibile calcolare le seguenti misure di posizione:
Moda
Mediana
Media aritmetica
d) Se possibile calcolare le seguenti misure di variabilità:
Differenza
Varianza
Scaro Quadratico
interquartile
Medio
Primo quartile
Coefficiente di
variazione
Terzo Quartile
Range
Sapendo che in Italia i dipendenti della stessa azienda hanno raggiunto questi risultati:
Media aritmetica
13.3
Scarto quadratico
medio
2
Comparare la situazione di Torino con quella nazionale in base al confronto degli indici forniti
_________________________________________________________________________________________
_________________________________________________________________________________________
_________________________________________________________________________________________
_________________________________________________________________________________________
_________________________________________________________________________________________
Esercizio 2
Utilizzando i dati dell’esercizio 1, valutare la dipendenza tra il “numero di nuovi contratti portati a termine” (Y)
e il “numero di nuovi clienti contattati” (X).
a) Individuare la retta dei minimi quadrati e valutarne la bontà di adattamento con R2
a = intercetta
b = coefficiente angolare
R2
b) Rappresentare in un grafico a dispersione le coppie (xi;yi) e la retta d’interpolazione, commentando i
risultati ottenuti
Grafico a dispersione e retta
Commenti:
____________________________________
____________________________________
____________________________________
____________________________________
____________________________________
____________________________________
____________________________________
____________________________________
____________________________________
____________________________________
____________________________________
Esercizio 3
Tra la clientela business di un istituto di credito, è possibile distinguere tra clienti provenienti da piccole o
medie imprese (PMI) e grandi imprese (GI). Tra questi clienti si sono verificati alcuni casi di insolvenza
(INS) secondo la seguente tabella:
PMI
GI
INS (insolventi)
10
6
SOL (solventi)
50
19
2
a) Valutare la probabilità che una azienda cliente sia una piccola o media impresa __________________
b) Valutare la probabilità che sia una grande impresa insolvente_________________________________
c) Valutare la probabilità di insolvenza tra le grandi imprese____________________________________
d) PMI e INS sono eventi indipendenti ?
Sì
No
Motivare la risposta fornita________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
Esercizio 4
In un impianto nucleare è avvenuto un incidente nella fase di raffreddamento del nucleo. In situazioni simili
è noto che la probabilità di contaminazione è pari a 0.02; sapendo che sono stati esposti 15 operai, valutare
la probabilità che:
a) nessun operaio sia stato contagiato__________________________________________________
b) un operario sia stato contagiato_____________________________________________________
c) almeno un operaio sia stato contagiato_______________________________________________
Esercizio 5 (solo per gli studenti da 8 CFU)
Per quanto riguarda la multinazionale di cui all’esercizio 1, si intende valutare il ricavo medio annuale di
mercato per ogni agente; si è quindi provveduto ad estrarre un campione di 60 agenti, rilevando che la media
campionaria è di 17000€ e lo scarto quadratico medio è pari a 1500€.
a) Valutare l’intervallo di confidenza per il ricavo medio annuale per l’intera popolazione degli agenti con
un livello di confidenza del 95%
______________________________________________________________________________________
b) Commentare il risultato ottenuto
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
3
Domande Teoriche
1) La variabilità: significato, misure ed esempi di utilizzo
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
2) Per disegnare un istogramma, nel caso di ampiezze di classe non siano omogenee, è necessario disegnare dei
rettangoli
a) contigui, le cui altezze siano proporzionali alle densità di frequenza
b) contigui, le cui altezze siano proporzionali alle frequenze assolute
c) separati, le cui altezze siano proporzionali alle frequenze relative
3) Se la media aritmetica della variabile statistica X, calcolata su un collettivo di numerosità 50, valesse µX=
100, come cambierebbe il suo valore se considerassimo altre ulteriori 25 unità statistiche per le quali la
variabile X assume valore pari a 70?
a) µX = 75
b) la media non è calcolabile
c) µX = 93.33
d) µX = 90
4) La retta dei minimi quadrati passa sempre per il punto (µx; µy)
a) vero
b) falso
5) Il tempo impiegato dal meccanico di un negozio di biciclette per assemblare un certo tipo di bicicletta può
essere considerato una v.c. normale con media 32 minuti e scarto quadratico medio 3,5 minuti. Si trovi la
probabilità che il meccanico assembli la bicicletta acquistata in un tempo minore di 32 minuti
a) 0,57046
b) 0,50000
c) 0, 11609
d) 0,61409
4