Circuiti elettrici (1' parte)
Il circuito elettrico più semplice è il seguente :
Naturalmente si possono costruire circuiti complicati quanto si vuole semplicemente inserendo
un numero qualsiasi di resistori o altri componenti elettrici non ancora da noi presi in
considerazione.
Si possono inserire nel circuito anche più generatori che possono essere anche generatori che
forniscono una tensione variabile nel tempo (fino ad ora abbiamo preso in considerazione solo
generatori di tensione continua, quali le comuni batterie che si possono acquistare ovunque).
In questa pagina mostriamo, fra tutti i possibili circuiti elettrici, quelli che presentano le seguenti
due caratteristiche :
- 1 - un solo generatore di tensione continua (almeno per un tempo sufficientemente lungo
se utilizzati correttamente)
- 2 - uno o più resistori ohmici (cioè che mantengono costante la resistenza a temperatura
costante al variare della corrente che li attraversa).
I resistori possono essere collegati in serie e/o in parallelo.
Prima di procedere, occorre però fare una precisazione sui generatori di tensione.
Un generatore di tensione (per esempio una comune batteria) possiede una resistenza elettrica
interna anche se molto piccola. Questo dipende dall'ovvio fatto che un generatore è costituito
esso stesso di materia e che quindi presenta una resistenza quando la corrente lo attraversa.
Un generatore è caratterizzato allora ai suoi capi da due tensioni :
- Una tensione a circuito aperto, cioè quando il generatore non è collegato ad alcun
circuito e quindi in esso (generatore) non circola corrente. Questa tensione è detta forza
elettromotrice (f.e.m.) e noi la indicheremo con la lettera
:
www.easymaths.altervista.org
(si noti la corrispondenza fra i punti
e
del "circuito reale" e del "circuito simbolico")
- Una tensione a circuito chiuso, cioè quando il generatore è collegato ad un circuito e
quindi in esso (generatore) circola corrente. Questa tensione (o differenza di potenziale) è quella
a cui "siamo già abituati" e che indicheremo come sempre con la lettera :
(si noti la corrispondenza fra i punti
e
del "circuito reale" e del "circuito simbolico")
(la resistenza interna del generatore è indicata con
)
Siccome la resistenza interna di un generatore è di solito molto piccola rispetto alle resistenze
presenti nel circuito, la forza elettromotrice è quasi uguale alla tensione ai capi del generatore
per cui possiamo scrivere :
.
Noi, quindi, per i nostri scopi, considereremo tali tensioni uguali ed useremo i simboli ed
indifferentemente (a meno che non sia necessario distinguerli, nel qual caso verrà messa in
evidenza la differenza fra le due grandezze).
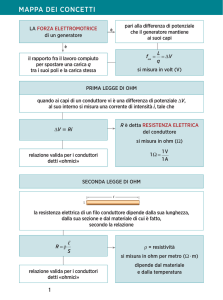
Ricordiamo qui anche le tre formule (ognuna ricavabile dall'altra) che legano la tensione
capi di un conduttore, la corrente
che vi circola e la sua resistenza
:
ai
www.easymaths.altervista.org
.
01 - Resistori in serie.
Consideriamo il seguente circuito :
(si noti il verso convenzionale della corrente dal + al - )
Si tratta di un circuito che presenta tre resistori collegati in serie, di resistenza
rispettivamente.
,
,
La caratteristica principale di questo circuito è che in ogni resistore passa la stessa corrente
che è la medesima che passa anche attraverso il generatore. Questo fatto molto importante si
spiega in questo modo :
le cariche elettriche che entrano nell'unità di tempo in un resistore sono le stesse che ne
escono (nell'unità di tempo) in quanto le cariche elettriche non possono essere "distrutte" o
"accumulate" dentro un resistore (essendo esso è un "semplice" conduttore).
Consideriamo i potenziali
,
,
,
nei punti del circuito indicati in figura :
www.easymaths.altervista.org
Si tratta dei potenziali ai capi dei resistori la conoscenza dei quali è molto importante per
comprendere il circuito. Si noti che i potenziali
e
(consideriamo la sua resistenza interna trascurabile).
sono i potenziali ai capi del generatore
Calcoliamo le tensioni ai capi dei tre resistori.
Siccome, come sopra affermato, la corrente
dove la tensione ai capi di
è
che circola nei tre resistori è la stessa, abbiamo :
(la tensione fra due punti è la differenza fra i rispettivi
potenziali, infatti tensione e differenza di potenziale sono sinonimi) , la tensione ai capi di
e la tensione ai capi di
è
è
.
Tali tensioni sono dette anche cadute di tensione.
Si noti che il potenziale
è maggiore del potenziale
e così via e questo per rispettare la
polarità del generatore (un punto più vicino al polo positivo avrà potenziale maggiore di un
punto più lontano).
Eseguiamo ora la somma in colonna delle tre relazioni scritte sopra partendo dall'evidente
presupposto che la somma dei termini a sinistra dell'uguale sarà identica alla somma dei termini
a destra.
Otteniamo perciò :
che si semplifica in :
www.easymaths.altervista.org
e in (raccogliendo
a fattore comune) :
.
Siccome
è la tensione ai capi del generatore che eguaglia
dal generatore), possiamo scrivere :
(cioè la tensione erogata
.
Questa formula significa che la tensione del generatore è uguale alla corrente che circola nel
generatore (ed in ogni resistore) moltiplicata per la somma della resistenze dei tre resistori.
Possiamo allora immaginare che i tre resistori collegati in serie siano equivalenti ad un unico
resistore la cui resistenza è uguale alla somma delle tre resistenze.
Se poniamo :
,
chiamando
resistenza totale, avremo :
.
Questa formula è identica a quella di un circuito con un solo resistore !!!
Il circuito in questione è quindi equivalente al seguente circuito dotato di un unico resistore con
resistenza uguale alla somma delle tre resistenze originali :
E' importante infine riassumere ciò che caratterizza un circuito di resistori collegati in serie :
www.easymaths.altervista.org
-1-
nei singoli resistori e nel generatore stesso circola la medesima corrente
- 2 - la somma delle cadute di potenziale ai capi dei resistori eguaglia la tensione del
generatore, cioè :
,
dove
qui rappresentano le cadute di potenziale ai capi dei rispettivi
resistori
-3-
la resistenza equivalente (totale) è data dalla somma delle resistenze cioè :
.
Consideriamo i seguenti esempi :
-1-
esempio
Nel caso del circuito con tre resistenze in serie, si abbia :
.
Calcoliamo subito la resistenza totale :
.
Essendo
, si ricava la corrente :
.
www.easymaths.altervista.org
La corrente che circola in ciascun resistore e nel generatore stesso è quindi di due ampere.
Calcoliamo infine le singole cadute di potenziale (le tensioni) ai capi dei singoli resistori. Abbiamo :
.
La caduta su
è di
(si può dire brevemente anche così) è di
, quella su
è di
, quella su
.
La somma delle tre cadute di potenziale eguaglia la tensione del generatore. Infatti :
come è giusto che sia.
-2-
esempio
Consideriamo una luminaria natalizia costituita da
lampadine (di tipo ordinario, ad
incandescenza e senza dispositivi interni contro l'interruzione dei circuiti) identiche ciascuna da
collegate in serie.
Supponendo che tale luminaria debba essere collegata alla tensione di rete di
, si determini il
numero
perché il circuito funzioni correttamente e si dica cosa succede se una lampadina si
fulmina.
(N.B. si dice che una lampadina è da
o qualunque altra tensione (che di solito è stampato in
trasparenza sulla lampadina stessa) quando il corretto ottimale funzionamento della lampadina lo si
ottiene a quella tensione. Questo non vuol dire che ad una lampadina non si possa applicare una
differente tensione. Se si applica alla lampadina una tensione inferiore a quella dichiarata si otterrà
meno luce o addirittura nessuna luce. Se si applica alla lampadina una tensione superiore a quella
dichiarata si otterrà più luce o addirittura la si potrà bruciare. In ogni modo, con una tensione
maggiore, la durata della lampadina potrà essere anche molto minore della durata media della
medesima alla tensione che il costruttore di solito dichiara. Una lampadina, in ogni caso, oppone
una resistenza alla corrente elettrica per cui è un resistore a tutti gli effetti (si tenga presente il
"fattore" temperatura che per una lampadina è di solito molto importante). Sulla lampadina sono
stampati anche altri dati fra cui la potenza in watt di cui parleremo più avanti in questo corso).
Evidentemente, per avere un funzionamento corretto della luminaria, il numero di lampadine è :
perché così la somma delle cadute di potenziale ai capi delle lampadine (
esattamente la tensione di rete (
).
per ognuna) uguaglia
www.easymaths.altervista.org
Se ne utilizzassimo un numero inferiore, avremmo che ai capi di ogni lampadina una caduta di
potenziale maggiore di
con il rischio di bruciarle.
Se ne utilizzassimo un numero superiore, avremmo che ai capi di ogni lampadina una caduta di
potenziale minore di
e questo produrrebbe meno luce.
Se una lampadina si fulmina, il circuito si interrompe e non passa più corrente. La luminaria,
ovviamente, si spegne.
02 - Resistori in parallelo.
Consideriamo il seguente circuito elettrico :
I due resistori di resistenza
ed
si dice che sono collegati in parallelo perché i loro
estremi sono collegati assieme nei punti
e .
Si ricorda che i tratti di circuito rappresentati da linee continue si suppone non abbiano resistenza
elettrica per cui è come se i due resistori fossero collegati direttamente al generatore, cioè i
capi
dei resistori sono collegati direttamente al polo positivo mentre i capi dei medesimi
sono collegati direttamente al polo negativo.
Questo significa che ai capi dei due resistori vi è la medesima tensione
generatore. Questo fatto caratterizza i resistori collegati in parallelo.
che è quella del
Di conseguenza, dentro i due resistori circoleranno correnti in generali diverse la cui somma, a
causa del principio di conservazione della carica, uguaglierà la corrente complessiva
che
passa nel generatore.
Avremo :
www.easymaths.altervista.org
per cui :
.
Intuitivamente, è come se la corrente, entrando nei due resistori, si "dividesse" (in generale in
parti diverse) e poi si "ricomponesse" uscendo da essi.
Le due correnti sono immediatamente calcolabili. Abbiamo :
essendo la tensione ai capi dei due resistori la stessa, ovvero la tensione
del generatore.
Vediamo il seguente esempio in cui abbiamo tre resistori in parallelo (ovviamente, le
considerazioni fatte per due resistori in parallelo valgono anche per
resistori in parallelo).
Sia il circuito :
(si noti il "simbolismo" lievemente diverso da quello usato nel precedente circuito, ma
equivalente)
www.easymaths.altervista.org
Le tre correnti sono date da :
.
Si noti che si hanno correnti minori dove la resistenza è maggiore, come è giusto che sia.
Definiamo ora la resistenza equivalente (o resistenza totale) di un certo numero
in parallelo.
di resistori
Sia il circuito :
Esso è equivalente a :
dove
è la resistenza equivalente degli
di resistori in parallelo.
Naturalmente si ha :
www.easymaths.altervista.org
e:
.
Diamo, senza dimostrazione, il valore della resistenza equivalente. Essa vale :
ovvero, l'inverso della resistenza equivalente di
inversi delle resistenze.
resistori in parallelo è la somma degli
Nel caso di due resistori, la formula può essere scritta in un'unica frazione (facendo il minimo
comune multiplo dei denominatori) :
dalla quale si ricava direttamente (invertendo le frazioni) la resistenza totale :
.
E' facile rendersi conto che la resistenza totale
ciascuna resistenza. Si ha cioè :
, per i resistori in parallelo, è minore di
.
Vediamolo matematicamente nel caso di due resistori in parallelo. In questo caso abbiamo :
www.easymaths.altervista.org
.
Verifichiamo che
. Avremo allora :
da cui si ha (dividendo ambo i membri per
e quindi (moltiplicando ambo i membri per
(che è positiva)) :
(che è positiva)) :
.
Questa disuguaglianza è sempre vera per cui è verificata l'affermazione. Lo stesso procedimento
per verificare che
.
Fisicamente si capisce che aggiungendo un resistore in parallelo si ottiene una resistenza
complessiva minore perché si aumenta la corrente totale a parità di tensione, essendo :
per cui, aumentando
diminuisce
, a parità di
Nel caso di due resistenze uguali (ciascuna di valore
.
) in parallelo si ha :
ovvero la resistenza totale è metà di una delle due come è giusto che sia.
Riassumiamo infine ciò che caratterizza un circuito di resistori collegati in parallelo :
www.easymaths.altervista.org
- 1 - la somma delle correnti che circolano nei resistori eguaglia la corrente che circola
nel generatore, cioè :
-2-
ai capi dei resistori vi è la stessa tensione, quella del generatore
-3-
la resistenza equivalente (totale) è data dalla formula :
.
Esempio.
Consideriamo i seguenti circuiti :
www.easymaths.altervista.org
Quali dei due circuiti è preferibile usare per misurare la tensione
ai capi di
e la corrente
che vi circola tenendo presente che
può essere "grande" o "piccola" mentre
(la resistenza
interna del voltmetro) è "grande" e
(la resistenza interna dell'amperometro) è "piccola" ?
Faremo considerazioni qualitative tenendo presente che per "grande" si intende "migliaia di ohm"
e per piccola si intende "pochi ohm".
-
piccola circuito
:
Il voltmetro, entro i limiti della propria precisione, misura
cadute di potenziale (che in generale valgono
, ovvero la somma delle
) su
e su
L'amperometro, entro i limiti della propria precisione, misura
Siccome
ed
Il circuito
, quindi, misura "bene"
-
sono comparabili, allora
piccola circuito
e
.
saranno comparabili.
ma misura "male"
.
:
Il voltmetro, entro i limiti della propria precisione, misura
.
L'amperometro, entro i limiti della propria precisione, misura
Siccome
è molto maggiore di
considerarsi trascurabile.
Il circuito
-
, quindi, misura "bene"
grande circuito
.
, allora
.
è molto maggiore di
e misura "bene"
per cui
può
.
:
www.easymaths.altervista.org
Il voltmetro, entro i limiti della propria precisione, misura
cadute di potenziale (che in generale valgono
, ovvero la somma delle
) su
e su
L'amperometro, entro i limiti della propria precisione, misura
Siccome
è molto maggiore di
considerarsi trascurabile.
Il circuito
-
, quindi, misura "bene"
grande circuito
, allora
.
è molto maggiore di
e misura "bene"
Il circuito
può
.
.
L'amperometro, entro i limiti della propria precisione, misura
e
per cui
:
l voltmetro, entro i limiti della propria precisione, misura
Siccome
.
sono comparabili, allora
, quindi, misura "male"
e
.
sono comparabili.
e misura "bene"
.
03 - Perché la resistenza interna di un amperometro deve essere piccola.
Consideriamo il semplice circuito :
e si voglia misurare con un amperometro la corrente
generatore).
che circola nel resistore (ed anche nel
Naturalmente si deve porre lo strumento in serie al resistore così che la stessa corrente che
circola nel resistore circolerà anche nello strumento il quale ne misurerà quindi l'intensità.
Il circuito sarà allora :
www.easymaths.altervista.org
Ma l'inserimento dello strumento ha modificato il circuito perché esso (lo strumento) contiene
una sua resistenza interna.
Si ottiene quindi che nel circuito ora circola la corrente :
che è evidentemente diversa dalla corrente originaria
. Esattamente ne è minore, cioè è :
.
L'introduzione dello strumento di misura ha inevitabilmente modificato, "disturbato",
"perturbato", il circuito originario e questo disturbo è ineliminabile.
Come deve essere allora la resistenza interna
perturbazione sia il più possibile trascurabile ?
dell'amperometro perché la suddetta
Evidentemente essa deve essere la più piccola possibile !!!
Se
(resistenza interna circa uguale a zero) si avrà :
ovvero :
.
Ecco perché gli amperometri hanno una resistenza interna piccola (di pochi ohm).
04 - Perché la resistenza interna di un voltmetro deve essere grande.
Consideriamo il semplice circuito :
www.easymaths.altervista.org
e si voglia misurare con un voltmetro la tensione
tensione erogata dal generatore).
ai capi del resistore (che uguaglia la
Naturalmente si deve porre lo strumento in parallelo al resistore.
Il circuito sarà allora :
Lo strumento così collegato misurerà direttamente la tensione
che circola nel circuito. La nuova corrente
sarà tale per cui :
ma modificherà la corrente
.
D'altra parte si ha :
per cui, sostituendo, possiamo scrivere :
www.easymaths.altervista.org
.
Se la resistenza interna del voltmetro
possiamo trascurarlo. Avremo allora :
è grande, il termine
è prossimo a zero per cui
ovvero :
.
Se la resistenza del voltmetro è grande, la corrente che circola nel circuito non viene modificata
dal suo inserimento.
Ecco perché i voltmetri hanno una resistenza interna grande (molte migliaia di ohm).
Circuiti elettrici (2' parte)
05 - Circuiti misti (resistori in serie e parallelo).
-1-
esempio
Consideriamo il seguente circuito :
Si calcolino le correnti e le cadute di potenziale relative ai tre resistori.
Esso presenta resistenze in serie ed in parallelo.
In questo circuito, la corrente
nel due resistori
ed
che passa per il generatore e per il resistore
, si divide in due correnti,
ed
, quando entra
, in modo che :
www.easymaths.altervista.org
.
Inoltre, la somma delle cadute di potenziale ai capi di
parallelo
dove con
ed
ed ai capi dei due resistori in
eguaglia la tensione del generatore
, cioè :
indichiamo la caduta di potenziale ai capi di
e con
potenziale ai capi dei due resistori in parallelo
ed
la caduta di
così come indicato nel grafico :
Per calcolare le correnti e le tensioni richieste si procede ricavando i successivi circuiti
equivalenti del circuito dato.
Il circuito equivalente a quello dato in cui le due resistenze in parallelo ,
considerate come un'unica resistenza, che chiameremo
Il valore di
ed
, sono
, è il seguente :
è dato da :
www.easymaths.altervista.org
da cui si ricava :
.
Il circuito equivalente al precedente in cui le due resistenze in serie ,
come un'unica resistenza, che chiameremo
Il valore di
e
, sono considerate
, è il seguente :
è dato da :
ovvero, sostituendo :
.
A questo punto siamo in grado di calcolare la corrente
. Avremo :
.
Per ricavare la caduta
basterà fare :
e per calcolare la caduta
:
.
Le correnti
ed
saranno date da :
www.easymaths.altervista.org
.
Abbiamo così ricavato tutti i dati richiesti.
Lasciamo al lettore la sostituzione nelle formule dei dati numerici consigliando infine di eseguire la
verifica dell'esattezza dei risultati ottenuti sostituendoli nelle formule
che "riassumono" correnti e tensioni per questo circuito.
-2-
,
esempio
Consideriamo il seguente circuito :
Si calcolino le correnti e le cadute di potenziale relative ai cinque resistori.
Per fare questo, procediamo, come nell'esempio - 1 -, individuando in sequenza i circuiti
equivalenti che si ricavano dal circuito originario.
Il circuito equivalente che si ottiene calcolando la resistenza equivalente
in serie
ed
delle resistenze
è il seguente :
www.easymaths.altervista.org
Per esso si ha :
.
Il circuito equivalente che si ottiene calcolando la resistenza equivalente
in parallelo
ed
delle resistenze
è il seguente :
Per esso si ha :
.
Il circuito equivalente che si ottiene calcolando la resistenza equivalente
serie
,
ed
delle resistenze in
è il seguente :
www.easymaths.altervista.org
Per esso si ha :
.
Ora siamo in grado di calcolare la corrente
generatore).
che circola nel circuito (in particolare nel
Avremo :
.
La caduta di potenziale
ai capi di
è:
.
La caduta di potenziale
ai capi di
è:
.
La caduta di potenziale
ai capi di
è:
.
La corrente
che circola in
è:
.
La corrente
che circola in
è:
www.easymaths.altervista.org
.
La caduta di potenziale
ai capi di
è:
ai capi di
è:
.
La caduta di potenziale
.
Si noti che :
.
Questo risultato, apparentemente errato, dipende dalle approssimazioni numeriche effettuate sopra.
-3-
esempio
Perché gli uccelli possono posarsi tranquillamente sui fili dell'alta tensione ?
I fili (i cavi) dell'alta tensione (o della distribuzione elettrica aerea in genere) non sono ricoperti
da alcun isolante. Gli uccelli, quindi, posandovisi sopra, vengono a "contatto" con la corrente che
circola nei fili che sicuramente potrebbe costituire un pericolo per la loro incolumità.
D'altra parte, se un uccello riuscisse a posare una zampa su un filo e l'altra su un altro,
risentirebbe di una grande differenza di potenziale e verrebbe fulminato all'istante. Questo, però,
può avvenire solo per volatili molto grandi perché i fili sono di solito sufficientemente distanziati.
Un uccello potrebbe posarsi su un filo e toccare con il becco o altra parte del corpo un
conduttore a differente potenziale in prossimità dell'isolante, per esempio questo potrebbe
avvenire nelle vicinanze di un isolante (strutture di vetro o ceramica o altro che serve per isolare
un filo dal suo sostegno) o strutture analoghe. In questo caso l'uccello rimarrebbe fulminato.
Consideriamo allora un uccello posato su un filo :
www.easymaths.altervista.org
Nel filo passa la corrente elettrica
alternata).
che supporremo continua (anche se nella realtà essa è
Contrariamente a quello che comunemente si pensa, attraverso l'animale passa una corrente
elettrica, seppur piccola.
Questa piccola corrente non gli reca alcun danno per cui i fili dell'alta tensione saranno sempre
prediletti dai pennuti per le loro comode soste ...
L'uccello possiede una propria resistenza interna
così come il tratto di filo
ha la propria
resistenza
(calcolabile facilmente usando la seconda legge di Ohm conoscendo resistività,
lunghezza e sezione del tratto
di conduttore).
Si può quindi introdurre il seguente schema che rappresenta il fenomeno :
www.easymaths.altervista.org
La corrente
viene quindi scomposta nella somma :
dove
è la corrente che passa per il volatile e
conduttore
.
La caduta di potenziale
scrivere :
è la corrente che passa nel tratto di
ai capi dei due resistori è evidentemente la stessa. Possiamo perciò
.
Abbiamo quindi ottenuto il sistema :
la cui soluzione ci fornisce le due correnti
corrente totale .
Ricaviamo
,
in funzione delle due resistenze
,
e della
dalla seconda equazione :
e sostituiamo nella prima :
.
Proseguendo nei calcoli si ottiene :
www.easymaths.altervista.org
(abbiamo eseguito il minimo comune multiplo dei denominatori di cui il
e trasformato in un'unica frazione)
secondo è
e:
(abbiamo raccolto a fattore comune
portandolo fuori dalla frazione)
da cui :
(abbiamo moltiplicato ambo i membri per il reciproco della frazione)
e:
cioè :
.
Riassumendo, le due correnti sono :
.
In particolare, a noi interessa la corrente che circola nel volatile :
.
Siccome la resistenza
del conduttore
è molto piccola (prossima a zero) e la resistenza
del volatile è molto grande (rispetto alla precedente), la formula può essere approssimata da :
.
www.easymaths.altervista.org
Questo dimostra che gli uccelli possono tranquillamente posarsi sui fili dell'alta tensione !!!
Se invece si avesse che le due resistenze sono comparabili, cioè
, avremmo :
cioè :
.
La corrente
si dividerebbe in due parti comparabili e la corrente
volatile lo ucciderebbe.
che passa attraverso il
Il problema può essere affrontato anche da altri punti di vista, ma si ottiene sempre lo stesso
risultato.
Possiamo, ad esempio, notare che fra le zampe dell'uccello, benché posate sullo stesso filo, esiste
una differenza di potenziale, corrispondente alla caduta di tensione fra i punti
e ai capi di
. Se la d.d.p. è molto piccola, sarà molto piccola (ma non nulla) anche la corrente elettrica che
attraverserà l'uccello. Vediamo di calcolarne l'ordine di grandezza.
La d.d.p. si calcola con la prima legge di Ohm :
.
La corrente i corrisponde con grande approssimazione alla corrente totale, che può arrivare da pochi
ampere a migliaia di ampere.
è la resistenza di un tratto di conduttore metallico lungo pochi centimetri e con la sezione che può
giungere a qualche centimetro quadrato. La sua resistenza, calcolata con la seconda legge di Ohm, è
dell'ordine di qualche milionesimo di ohm.
Se ci mettiamo in un caso molto sfavorevole per l'uccello, cioè con una corrente di
, dalla
legge di Ohm
ricaviamo che la tensione fra i punti
e è dell'ordine dei millivolt,
cioè estremamente bassa.
Poiché la resistenza elettrica dell'uccello può essere stimata in qualche migliaio di ohm, risulta che
la corrente che attraversa il volatile
, sarà inferiore al milionesimo di ampere.
Si tratta di una corrente estremamente bassa, non avvertita dall'uccello, ma non nulla.
Se si pensa che la corrente di un ampere corrisponde al passaggio attraverso la sezione di un
conduttore di un coulomb al secondo, cioè di sei miliardi di miliardi di elettroni al secondo,
www.easymaths.altervista.org
attraverso la sezione delle zampe del nostro uccello c'è comunque un passaggio di miliardi di
elettroni al secondo.
La situazione per i volatili potrebbe diventare preoccupante se
diventa abbastanza grande in
modo da far aumentare in modo significativo la caduta di tensione ai suoi capi.
Per aumentare il valore di
occorre aumentare la sua lunghezza e diminuire la sua sezione. La
lunghezza, corrispondente alla distanza fra le zampe dell'uccello, resta di solito entro la decina di
centimetri. La sezione non può diventare troppo piccola per motivi legati alla resistenza meccanica
ed elettrica del conduttore.
Gli uccelli di piccole dimensioni possono dormire sonni tranquilli sui fili dell'alta tensione. Quelli
maggiori possono correre dei rischi a causa dell' apertura alare che potrebbe portarli a toccare o
sfiorare contemporaneamente punti ad elevata differenza di potenziale.
www.easymaths.altervista.org