C3. Rette parallele e perpendicolari - Esercizi
ESERCIZI CON COSTRUZIONI E GRAFICI
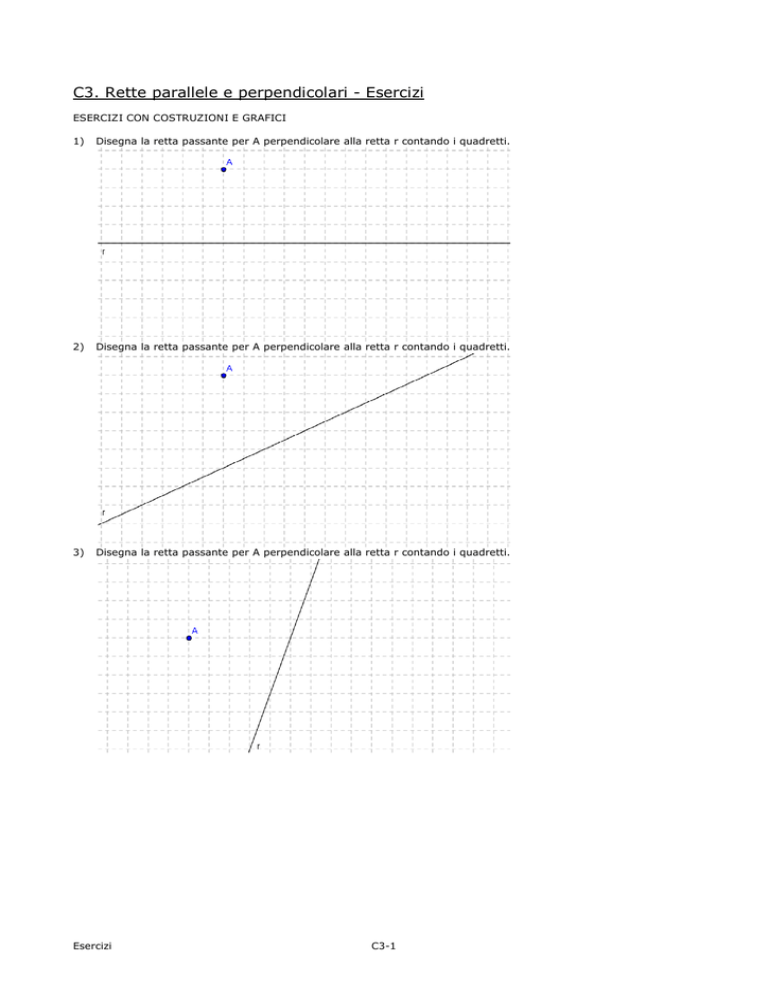
1)
Disegna la retta passante per A perpendicolare alla retta r contando i quadretti.
2)
Disegna la retta passante per A perpendicolare alla retta r contando i quadretti.
3)
Disegna la retta passante per A perpendicolare alla retta r contando i quadretti.
Esercizi
C3-1
4)
Disegna la retta passante per A perpendicolare alla retta r con riga e compasso.
5)
Disegna la retta passante per A perpendicolare alla retta r con riga e compasso.
6)
Disegna la retta passante per A perpendicolare alla retta r con riga e compasso.
7)
Determina la proiezione del punto A sulla retta r contando i quadretti.
Esercizi
C3-2
8)
Determina la proiezione del punto A sulla retta r contando i quadretti.
9)
Determina la proiezione del punto A sulla retta r contando i quadretti.
10) Determina la proiezione del punto A sulla retta r con riga e compasso.
11) Determina la proiezione del punto A sulla retta r con riga e compasso.
Esercizi
C3-3
12) Determina la proiezione del punto A sulla retta r con riga e compasso.
13) Trova un segmento congruente ad AB tale che la sua proiezione sulla retta r sia il segmento A’B’.
14) Trova un segmento congruente ad AB tale che la sua proiezione sulla retta r sia il segmento A’B’.
15) Dire quale segmento rappresenta la distanza di A da r, AB, AC o AD?
Esercizi
C3-4
16) Dire quale segmento rappresenta la distanza di A da r, AB o AC?
17) Disegna la retta passante per A parallela alla retta r contando i quadretti.
18) Disegna la retta passante per A parallela alla retta r contando i quadretti.
19) Disegna la retta passante per A parallela alla retta r contando i quadretti.
Esercizi
C3-5
20) Disegna la retta passante per A parallela alla retta r con riga e compasso.
21) Disegna la retta passante per A parallela alla retta r con riga e compasso.
22) Disegna la retta passante per A parallela alla retta r con riga e compasso.
23) Data la seguente figura completa al posto dei puntini.
Esercizi
C3-6
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
e
e
e
e
e
e
e
e
e
e
e
e
e
e
e
e
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
alterni interni.
alterni interni.
alterni esterni.
alterni esterni.
coniugati interni.
coniugati interni.
coniugati esterni.
coniugati esterni.
corrispondenti.
corrispondenti.
corrispondenti.
corrispondenti.
opposti al vertice.
opposti al vertice.
opposti al vertice.
opposti al vertice.
24) Data la seguente figura completa al posto dei puntini.
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
Gli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
angoli
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
e
e
e
e
e
e
e
e
e
e
e
e
e
e
e
e
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
_____
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
sono
alterni interni.
alterni interni.
alterni esterni.
alterni esterni.
coniugati interni.
coniugati interni.
coniugati esterni.
coniugati esterni.
corrispondenti.
corrispondenti.
corrispondenti.
corrispondenti.
opposti al vertice.
opposti al vertice.
opposti al vertice.
opposti al vertice.
25) Sapendo che r ed s sono parallele tagliate dalla trasversale t, dire se gli angoli indicati sono congruenti o
supplementari.
α e β’ sono
α e γ sono
Esercizi
________________
________________
C3-7
α e γ’ sono
α e α’ sono
δ e β sono
δ e β’ sono
δ’ e β sono
δ e γ sono
δ e γ’ sono
δ e α’ sono
________________
________________
________________
________________
________________
________________
________________
________________
26) Sapendo che r ed s sono parallele tagliate dalla trasversale t, dire se gli angoli indicati sono congruenti o
supplementari.
ˆ sono
ˆ e CGH
DHG
________________
ˆ sono
ˆ e FGC
DHG
________________
ˆ e AHE
ˆ sono
DHG
________________
ˆ e DHA
ˆ sono
DHG
________________
ˆ sono
ˆ e FGC
DHA
________________
ˆ sono
ˆ e FGB
DHA
________________
ˆ sono
ˆ e BGH
DHG
________________
ˆ e AHE
ˆ sono
FGB
________________
27) Trova tutti gli angoli in figura in funzione di α.
Esercizi
C3-8
28) Sapendo che l’angolo indicato è 103° determina le ampiezze di tutti gli angoli in figura.
29) Determina le ampiezze di tutti gli angoli in figura in funzione di α sapendo che il triangolo è isoscele.
ˆ , BCD
ˆ e
30) Sapendo che BAC è isoscele con base BC e che BCD è isoscele con base BD determina l’ampiezza di BCA
ˆ in funzione di α.
CDB
31) Determina le ampiezze di tutti gli angoli in figura sapendo che il triangolo è isoscele.
Esercizi
C3-9
ˆ .
32) Determina le ampiezze di tutti gli angoli in figura sapendo che r è la bisettrice di BCA
ˆ , BCD
ˆ e
33) Sapendo che BAC è isoscele con base BC e che BCD è isoscele con base BD determina l’ampiezza di BCA
ˆ sapendo che α=136°.
CDB
34) Conoscendo gli angoli indicati in figura determinare tutti gli altri.
35) Sapendo che ABC è un triangolo equilatero e che BCD è rettangolo isoscele determinare l’ampiezza del’angolo
ACD.
Esercizi
C3-10
36) Trova l’ampiezza degli angoli interni di un pentagono.
37) Determina l’ampiezza dell’angolo α.
38) Trova l’ampiezza degli angoli interni di un esagono.
39) Determina l’ampiezza dell’angolo α.
40) Trova l’ampiezza degli angoli interni di un ottagono.
41) Determina l’ampiezza dell’angolo α.
42) Trova l’ampiezza degli angoli interni di un decagono.
43) Determina l’ampiezza dell’angolo α.
Esercizi
C3-11
DIMOSTRAZIONI
ˆ si costruiscano gli angoli ABD
ˆ e EBC
ˆ retti esterni all’angolo convesso ABC
ˆ . Si
44) Dato l’angolo ottuso α = ABC
ˆ e l’angolo α = ABC
ˆ sono supplementari.
dimostri che l’angolo EBD
45) Sia ABC un triangolo isoscele di base AB. Sia D∈AB. Si tracci la retta t passante per D perpendicolare ad AB (non
passante per C) e si traccino la retta r passante per A e C e la retta s passante per B e C. Si dimostri che la retta t
incontra la retta r e la retta s in due punti E ed F equidistanti da C.
46) Dato un triangolo isoscele ABC si tracci la retta r parallela ad AB passante per C e si tracci la retta s passante per
AC. Si dimostri che la retta r è la bisettrice dell’angolo formato dalla retta s e dalla retta passante per B e C.
47) Dato un triangolo isoscele ABC si prolunghi il lato AC dal lato di C di un segmento CE. Si dimostri che la bisettrice
ˆ è parallela al lato AB.
dell’angolo BCE
ˆ e BAC
ˆ che si incontrano in un punto O. Si tracci
48) Dato un triangolo ABC si conducano le bisettrici agli angoli ABC
la retta parallela ad AB passante per O, che interseca i lati AC e BC rispettivamente in D ed E. Si dimostri che
DE≅AD+BE.
49) In un triangolo ABC la bisettrice dell’angolo esterno avente vertice A è parallela al lato BC. Si dimostri che il
triangolo ABC è isoscele e dire qual è la base e quali sono i lati obliqui.
50) Dato un triangolo isoscele di base AB si traccino la retta r passante per A parallela a BC, la retta s passante per B
parallela ad AC e la retta t passante per C parallela ad AB. Si dimostri che il triangolo formato dalle rette r, s e t è
isoscele.
51) Dato un triangolo rettangolo ABC retto in C si traccino le bisettrici degli angoli esterni ad A e B. Tali bisettrici si
incontrano in D. Si traccino la retta r passante per A e C, la retta s passante per B e C e la retta t passante per D
parallela ad AB. La retta r e la retta t si incontrano in E mentre la retta s e la retta t si incontrano in F. Si dimostri
che EF≅EA+BF.
52) Dato un triangolo ABC si consideri il punto medio M di AB. Si tracci l’asse di simmetria del segmento AM che
interseca il lato AC in D. Si dimostri che se DM è parallelo a BC allora ABC è isoscele.
53) Dato un triangolo ABC isoscele di base AB si traccino gli assi del segmento AB (che passa per M∈AB) e l’asse del
segmento AM che interseca il lato AC in D. Si dimostri che MD è parallelo a BC.
54) Dato un triangolo ABC equilatero si tracci una retta parallela ad AB che intersechi AC e BC in M ed N
rispettivamente. Si dimostri che il triangolo CMN è equilatero.
55) Dato il triangolo ABC si tracci la parallela ad AB passante per C e su essa si fissi un punto D tale che CD≅CB. Si
dimostri che BD è parallela ad AC oppure BC è parallela ad AD.
56) Dato un triangolo isoscele ABC sulla base AB si prolunghi il segmento BC di un segmento CD≅BC. Si dimostri che
ˆ è retto.
l’angolo BAD
ˆ si tracci la bisettrice dell’angolo e su di essa si prenda un punto D. Si traccino le proiezioni E
57) Dato un angolo ABC
ed F di D sui lati dell’angolo. Si dimostri che DF≅DE.
Esercizi
C3-12












