Università degli Studi di Salerno

Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Università degli Studi di Salerno
Facoltà di Scienze Matematiche Fisiche e Naturali
Tesina di Ottimizzazione
Anno Accademico 2011/2012
Optimization Toolbox di Matlab:
Studio delle più importanti funzioni che il tool mette a disposizione, degli algoritmi
utilizzati e applicazione del software a problemi di test reperibili in rete.
Studente:
Gianluca Carbone
0522500116
Professore:
Giancarlo Raiconi
1
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Indice
1. Che cos’ è Optimization Toolbox __________________________________4
-
Introduzione e funzionalità chiave
Definizione, soluzione e valutazione di problemi di ottimizzazione
Programmazione non lineare
Ottimizzazione multi obiettivo
Minimi quadrati, fitting dei dati ed equazioni non lineari
Programmazione lineare
Programmazione binaria intera
Programmazione quadratica
Ricsoluzione di problemi di ottimizzazione usando il calcolo parallelo
2. Overview____________________________________________________17
-
Uso delle funzioni di ottimizzazione
Medium – Scale ( or Standard) algorithm
Large Scale algorithm
Funzioni disponibili
3. Funzioni in categorie e Input/Output_____________________________20
- Funzioni in categorie
- Input/Output
4. Algoritmi Standard___________________________________________26
-
Gradient Methods
Quasi – Newton Methods
Aggiornamento Hessiano
Procedure di linea di ricerca
Ottimizzazione con i minimi quadrati
Metodo Gauss – Newton
Metodo di Levemberg – Marquardt
Implementazione minimi quadrati non lineari
2
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
5. Algoritmi su larga scala_______________________________________34
-
Metodi Trust – Region per minimizzazione non lineare
Gradienti coniugati precondizionati
Minimi quadrati non lineari
Minimi Quadrati lineari
6. My functions ( qualche funzione in dettaglio)_______________________38
- Minimizzazione non vincolata non lineare ( fminsearch, fminunc )
- Minimi quadrati lineari e non lineari ( lsqlin, lsqnonlin )
3
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
1. Che cos’è Optimization Toolbox
E una collezione di funzioni che estendono la capacità dell'ambiente di calcolo
numerico di Matlab. La toolbox include procedure per molti tipi di ottimizzazione tra
cui:
• Minimizzazione non lineare non vincolata;
• Minimizzazione non lineare vincolata, tra cui problemi goal attainment,
problemi minimax e problemi di minimizzazione semi- infinita;
• Programmazione quadratica e lineare;
• Minimi quadrati e curve-fitting non lineari;
• Risoluzione di sistemi di equazioni non lineari;
• Minimi quadrati lineari vincolati;
• Problemi su larga scala sparsi e strutturati.
Tutte le funzioni sono M-files di Matlab , costituiti di dichiarazioni che
implementano algoritmi specializzati di ottimizzazione.
E’ possibile vedere il codice Matlab di queste funzioni usando la dichiarazione " type
function_name " .
E’ possibile estendere le capacità di Optimization Tolbox scrivendo proprie funzioni
Matlab, o usando il toolbox in combinazione con altri toolboxes con Matlab o
Simulink (Simulink® è un ambiente per la simulazione multidominio e per la
progettazione basata sulla modellazione per sistemi dinamici e integrati. Mette a
disposizione un'interfaccia grafica interattiva e una serie di librerie personalizzabili
per sviluppare, simulare, implementare e testare numerose categorie di sistemi
variabili nel tempo, comprendenti tematiche quali comunicazioni elettriche, controlli,
elaborazione di segnali, video e immagini.).
1.1
Introduzione e funzionalità chiave
Optimization Toolbox™ fornisce algoritmi di uso comune per ottimizzazioni
standard e su larga scala. Questi algoritmi risolvono problemi discreti e continui,
vincolati e non. La toolbox comprende funzioni per la programmazione lineare,
quadratica, binaria intera, ottimizzazione non lineare, minimi quadrati non lineari,
4
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
sistemi di equazioni non lineari e ottimizzazione multiobiettivo. Sono disponibili
funzioni per identificare le soluzioni ottimali, eseguire l'analisi di bilanciamento,
equilibrare le molteplici alternative progettuali e incorporare i metodi di
ottimizzazione in algoritmi e modelli.
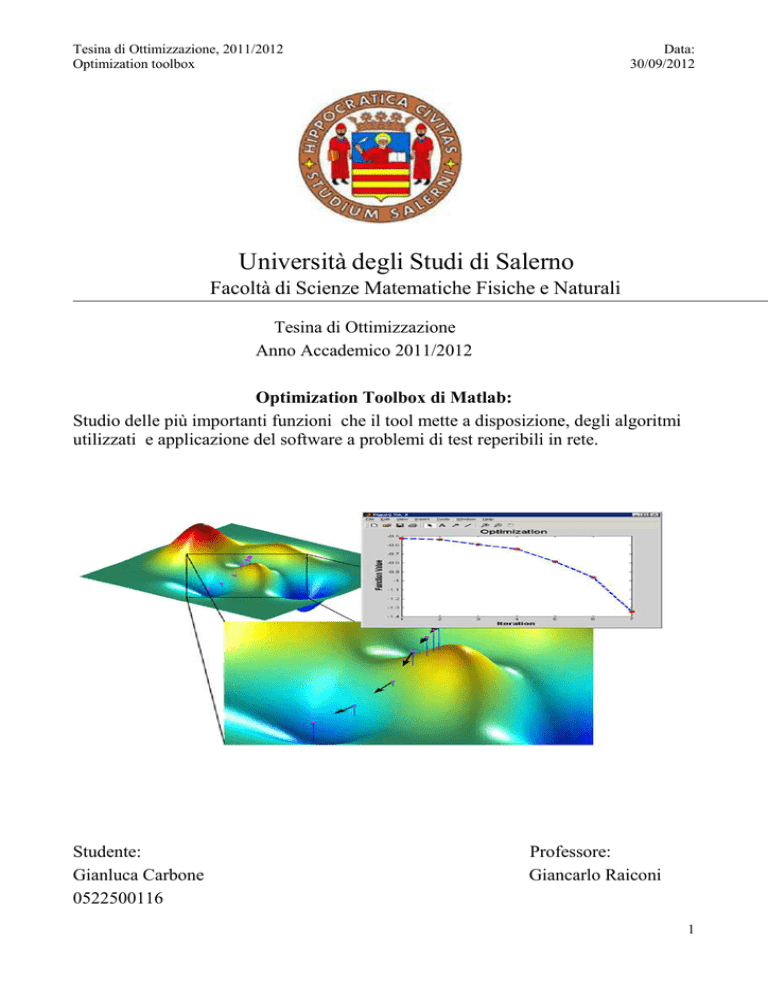
Individuazione di una minima locale della funzione peaks utilizzando un solutore di ottimizzazione basato su
gradiente fornito da Optimization Toolbox.
Funzionalità chiave
•
•
•
•
•
•
Strumenti interattivi per definire e risolvere problemi di ottimizzazione e
monitorare il progresso verso la soluzione
Solutori per ottimizzazione non lineare e multiobiettivo
Solutori dei minimi quadrati non lineari, fitting dei dati ed equazioni non
lineari
Metodi per risolvere problemi di programmazione quadratici e lineari
Metodi per risolvere problemi di programmazione binaria intera
Supporto del calcolo parallelo nei solutori non lineari vincolati selezionati
5
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Un'immagine sfocata restaurata mediante l'algoritmo dei minimi quadrati lineari su larga scala
1.2
Definizione, soluzione e valutazione di problemi di ottimizzazione
Optimization Toolbox comprende molti dei metodi più comuni per la minimizzazione
e la massimizzazione. La toolbox implementa algoritmi sia standard sia su larga scala
per consentire di risolvere i problemi sfruttando la sparsità o la struttura. Le funzioni
e i solutori del toolbox sono accessibili da Optimization Tool o dalla riga di comando.
Una routine di ottimizzazione eseguita dalla riga di comando (a sinsitra) per chiamare file MATLAB
definendo la funzione obiettivo (a destra) e le equazioni di vincolo (a destra).
Optimization Tool semplifica molte operazioni di ottimizzazione comuni.
Consente di:
•
•
•
•
•
•
•
1.3
selezionare un solutore e definire un problema di ottimizzazione;
impostare e ispezionare le opzioni di ottimizzazione con i rispettivi valori
predefiniti per il solutore selezionato;
eseguire i problemi e visualizzare i risultati intermedi e finali;
visualizzare la documentazione specifica del solutore in una finestra opzionale
di riferimento rapido;
importare ed esportare le definizioni dei problemi, le opzioni dell'algoritmo e i
risultati tra il workspace MATLAB e Optimization Tool;
generare automaticamente il codice MATLAB per registrare il lavoro svolto e
automatizzare le operazioni;
accedere ai solutori di Global Optimization Toolbox.
Programmazione non lineare
6
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Optimization Toolbox fornisce algoritmi di ottimizzazione di uso diffuso per
risolvere problemi della programmazione non lineare in MATLAB. La toolbox
include solutori per l'ottimizzazione non lineare vincolata e non e solutori per
l'ottimizzazione dei minimi quadrati.
Ottimizzazione non lineare non vincolata
Optimization Toolbox utilizza tre algoritmi per risolvere problemi di ottimizzazione
non lineare non vincolata:
•
•
•
l'algoritmo Quasi-Newton utilizza una procedura di ricerca lineare mista
quadratica e cubica e la formula di Broyden-Fletcher-Goldfarb-Shanno (BFGS)
per aggiornare l'approssimazione della matrice hessiana;
l'algoritmo di Nelder-Mead è un algoritmo a ricerca diretta che utilizza
solamente i valori della funzione (non richiede il calcolo delle derivate) e
agisce sulle funzioni obiettivo non-smooth. Global Optimization
Toolbox fornisce altri algoritmi di ottimizzazione senza calcolo delle derivate
per l'ottimizzazione non lineare;
l'algoritmo trust-region viene utilizzato per problemi non lineari non vincolati,
soprattutto per problemi su larga scala in cui sia possibile sfruttare la sparsità o
la struttura.
Programmazione non lineare non vincolata utilizzata per la ricerca dell'efficienza di picco in una mappa di
performance di un motore.
Ottimizzazione non lineare vincolata
I problemi di ottimizzazione non lineare vincolata sono composti da funzioni
obiettivo non lineari e possono essere soggetti a vincoli lineari e non lineari.
Optimization Toolbox utilizza quattro algoritmi per risolvere i seguenti problemi.
7
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
•
•
•
•
Data:
30/09/2012
L'algoritmo a punto interno viene utilizzato per l'ottimizzazione non lineare
generale. È soprattutto utile per problemi su larga scala con sparsità o struttura
e tollera errori di valutazione nella funzione obiettivo definita dall'utente e
nella funzione di vincolo. Si basa su una funzione di barriera e, a scelta,
assicura la fattibilità di tutte le iterate rispetto ai contorni durante
un'ottimizzazione.
L'algoritmo SQP viene utilizzato per l'ottimizzazione non lineare generale.
Rispetta i contorni e tutte le iterazioni e tollera errori di valutazione nella
funzione obiettivo definita dall'utente e nella funzione di vincolo.
L'algoritmo active-set viene utilizzato per l'ottimizzazione non lineare
generale.
L'algoritmo riflessivo trust-region viene utilizzato solamente per problemi
con vincoli al contorno o con uguaglianze lineari. È utile soprattutto per
problemi su larga scala.
L'algoritmo a punto interno e l'algoritmo riflessivo trust-region consentono di
calcolare gli hessiani con approcci diversi.
Per l'algoritmo a punto interno, è possibile stimare gli hessiani usando:
•
•
•
•
•
BFGS (densa);
BFGS a memoria ridotta (per problemi su larga scala);
funzione di moltiplicazione hessiana;
hessiana reale (sparsa o densa);
differenza finita di gradienti, senza necessità di conoscenza della struttura di
sparsità.
Per l'algoritmo riflessivo trust-region, è possibile usare:
•
•
•
differenza finita di gradienti, hessiana con conoscenza della struttura di
sparsità;
hessiana reale (sparsa o densa);
funzione di moltiplicazione hessiana.
Inoltre, gli algoritmi punto interno e riflessivo trust-region consentono di calcolare i
prodotti tra la matrice hessiana e un vettore senza dover allocare esplicitamente la
matrice stessa.
Optimization Toolbox include inoltre un'interfaccia per le librerie KNITRO di Ziena
Optimization per la soluzione di problemi di ottimizzazione non lineari vincolati.
8
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Programmazione non lineare vincolata utilizzata per progettare un sistema di sospensioni ottimale.
1.4
Ottimizzazione multiobiettivo
L'ottimizzazione multiobiettivo si concentra sul minimizzare le funzioni
multiobiettivo soggette a una serie di vincoli. Optimization Toolbox fornisce le
funzioni per la soluzione di due formulazioni di problemi di ottimizzazione
multiobiettivo.
•
•
Il problema del raggiungimento degli obiettivi riguarda la riduzione del
problema di una funzione vettoriale lineare o non lineare per raggiungere i
valori obiettivo di un vettore obiettivo. L'importanza relativa degli obiettivi è
indicata tramite un vettore di pesi. Il problema del raggiungimento degli
obiettivi può anche essere soggetto a vincoli lineari e non lineari.
Il problema minimax riguarda la minimizzazione del valore di caso peggiore
di una serie di funzioni multivariate eventualmente soggetto a vincoli lineari e
non lineari.
Optimization Toolbox trasforma entrambi i tipi di problemi multiobiettivo in normali
problemi di ottimizzazione vincolata, quindi li risolve secondo un approccio activeset.
Global Optimization Toolboxfornisce un ulteriore solutore multiobiettivo per
problemi non-smooth.
9
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Ottimizzazione multiobiettivo utilizzata per progettare un filtro passa-basso.
1.5
Minimi quadrati, fitting dei dati ed equazioni non lineari
Optimization Toolbox è in grado di risolvere problemi di minimi quadrati non lineari,
problemi di fitting dei dati ed equazioni non lineari.
Ottimizzazione lineare e non lineare dei minimi quadrati
La toolbox utilizza due algoritmi per risolvere i problemi di minimi quadrati lineari:
•
•
l'algoritmo di media scala implementa un algoritmo active-set e viene
utilizzato per risolvere problemi con contorni e uguaglianze o disuguaglianze
lineari;
l'algoritmo di larga scala implementa un algoritmo riflessivo trust-region e
viene utilizzato per risolvere problemi aventi solo vincoli al contorno.
La toolbox utilizza due algoritmi per risolvere i problemi di minimi quadrati non
lineari:
•
l'algoritmo riflessivo trust-region implementa l'algoritmo di LevenbergMarquardt utilizzando un approccio trust-region. Viene utilizzato per problemi
non vincolati e con vincoli al contorno;
10
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
•
Data:
30/09/2012
l'algoritmo di Levenberg-Marquardt implementa un metodo standard di
Levenberg-Marquardt. Viene utilizzato per problemi non vincolati.
Fitting di un'equazione trascendentale utilizzando i minimi quadrati non lineari.
Fitting dei dati
La toolbox comprende anche un'interfaccia specializzata per problemi di fitting dei
dati nei quali si vuole trovare il rappresentante più adatto di una famiglia di funzioni
non lineari per un set di punti di dati. La toolbox utilizza gli stessi algoritmi per
risolvere i problemi di fitting dei dati utilizzati per i problemi di minimi quadrati non
lineari.
Fitting di un'equazione esponenziale non lineare mediante la curva dei minimi quadrati.
11
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Soluzione di equazioni non lineari
Optimization Toolbox implementa un algoritmo trust-region "dogleg" per risolvere
un sistema di 'n' equazioni non lineari. La toolbox è anche in grado di risolvere questo
tipo di problemi utilizzando l'algoritmo riflessivo trust-region o l'algoritmo di
Levenberg-Marquardt.
Soluzione di una funzione Rosenbrock n-dimensionale utilizzando il solutore per equazioni non lineari.
1.6
Programmazione lineare
Ingegneri e scienziati usando la modellazione matematica per descrivere il
comportamento dei sistemi oggetto di studio. I requisiti di sistema, quando definiti
matematicamente come vincoli sugli input delle variabili decisionali all'interno del
modello di sistema matematico, formano un programma matematico. Tale
programma matematico, o descrizione del problema di ottimizzazione, può poi essere
risolto usando le tecniche di ottimizzazione. La programmazione lineare è una classe
di programmi matematici in cui l'obiettivo e i vincoli sono relazioni lineari.
I problemi di programmazione lineare riguardano un'espressione lineare per la
funzione obiettivo e vincoli di uguaglianza o disuguaglianza lineare. Optimization
Toolbox include tre algoritmi utilizzati per risolvere questo tipo di problemi.
12
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
•
•
•
Data:
30/09/2012
L'algoritmo punto interno si basa su un algoritmo predittore-correttore
primario-duale utilizzato per risolvere problemi della programmazione lineare.
È utile soprattutto per problemi su larga scala strutturati o definibili mediante
matrici sparse.
L'algoritmo active-set minimizza l'obiettivo a ciascuna iterazione di tutto il set
attivo (un subset dei vincoli attivi localmente) fino a convergere in una
soluzione.
L'algoritmo simplesso è una procedura sistematica per generare e testare le
soluzioni al vertice candidate di un programma lineare. L'algoritmo simplesso
è quello maggiormente utilizzato per la programmazione lineare.
Programmazione lineare utilizzata nella progettazione di un impianto di generazione di vapore ed energia
elettrica.
1.7
Programmazione binaria intera
I problemi di programmazione binaria intera riguarda la minimizzazione di una
funzione obiettivo lineare soggetta a vincoli di uguaglianza o disuguaglianza lineare.
Ogni variabile della soluzione ottimale deve assumere il valore 0 o 1.
Optimization Toolbox risolve questi problemi utilizzando un algoritmo di
enumerazione implicita (Branch and Bound) che:
•
•
•
ricerca una soluzione intera binaria praticabile;
aggiorna il miglior punto binario trovato via via che l'albero di ricerca cresce;
verifica che non esista una soluzione migliore, risolvendo una serie di problemi
di rilassamento della programmazione lineare.
13
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Programmazione binaria intera utilizzata per risolvere un problema di investimento.
1.8
Programmazione quadratica
I problemi di programmazione quadratica riguardano la minimizzazione di una
funzione quadratica multivariata soggetta a limiti e vincoli di uguaglianza lineare e di
disuguaglianza. Optimization Toolbox contiene tre algoritmi per la soluzione di
programmi quadratici:
•
•
•
l'algoritmo convesso a virgola interna risolve problemi complessi con
qualsiasi combinazione di vincoli;
l'algoritmo riflessivo trust-region risolve problemi con vincoli di limite o
problemi con vincoli di uguaglianza lineare;
l'algoritmo active-set risolve problemi con qualsiasi combinazione di vincoli.
Sia l'algoritmo convesso a virgola interna che quello riflessivo trust-region sono su
larga scala, ossia possono gestire problemi di ampie dimensioni e sparsi. Inoltre,
l'algoritmo convesso a virgola interna ha routine algebriche lineari ottimizzate e un
nuovo modulo di presoluzione che può migliorare la velocità, la stabilità numerica e
la rilevazione dell'infattibilità.
14
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Programmazione quadratica utilizzata per eseguire un'analisi di stile basata sulla redditività di tre fondi
d'investimento.
1.9
Risoluzione di problemi di ottimizzazione usando il calcolo parallelo
Optimization Toolbox può essere utilizzata insieme a Parallel Computing
Toolbox per risolvere problemi che possono trarre vantaggio dal calcolo parallelo. È
possibile abilitare il supporto integrato del calcolo parallelo per ridurre i tempi
necessari alla soluzione oppure definendo un'implementazione di calcolo parallelo
personalizzata di un problema di ottimizzazione.
Il supporto integrato per il calcolo parallelo in Optimization Toolbox consente di
velocizzare la fase di stima del gradiente in solutori specifici per problemi di
ottimizzazione non lineare vincolata e per problemi multiobiettivo di raggiungimento
degli obiettivi e minimax.
15
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Accelerazione del tempo della soluzione di un problema elettrostatico utilizzando il supporto integrato per
calcolo parallelo in un solutore di programmazione non lineare. La funzionalità integrata viene abilitata
specificando l'opzione UseParallel (a sinistra) per le funzioni obiettivo (al centro a destra) e vincolo (in basso
a destra). La soluzione è mostrata in alto a destra.
È possibile personalizzare un'implementazione di calcolo parallelo definendo
esplicitamente il problema di ottimizzazione per l'utilizzo della funzionalità di calcolo
parallelo. È possibile definire una funzione obiettivo o una funzione vincolo per
utilizzare il calcolo parallelo, e ciò consente di ridurre il tempo necessario per
valutare l'obiettivo o il vincolo.
Accelerazione del tempo di soluzione (in alto a destra) per il progetto di un sistema di sospensioni (in basso a
sinistra e a destra) soggetto ad aleatorietà, personalizzando la funzione obiettivo con una semplice modifica
di una riga del codice (in alto a sinistra).
16
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
2.
Overview
2.1
Uso delle funzioni di ottimizzazione
Data:
30/09/2012
Molte di queste procedure richiedono la definizione di un M-file contenente la
funzione che deve essere minimizzata, ad esempio la funzione obbiettivo.
Alternativamente , è possibile utilizzare un oggetto inline creato da Matlab. La
massimizzazione è ottenuta fornendo la routine con –f, dove f è la funzione da
ottimizzare.
L’ ‘option’ di ottimizzazione passata alla procedura cambia i parametri di
ottimizzazione. I parametri di default sono utilizzati ampiamente ma è possibile
cambiarli attraverso la struttura options.
Il gradienti sono calcolati usando un metodo adattivo a differenza –finita a meno che
sono forniti in una funzione. I parametri possono essere passati direttamente alle
funzioni evitando la necessità di variabili globali.
Separiamo gli algoritmi su “media-scala” da gli algoritmi su “larga-scala”. Media scala non è un termine standard ed esso è usato solo per differenziare questi
algoritmi da quelli a larga scala che sono progettati per gestire problemi efficienti su
larga scala .
2.2
Medium-Scale (or Standard) Algorithm
Le routines di optimization tool offre una scelta di algoritmi e linea di ricerca di
strategie. I principali algoritmi per la minimizzazione non vincolata sono i metodi di
ricerca del simplesso Nelder –Mead e il metodo Quasi –newton di BFGS
(Broyden,flecher,Goldfarb e Shanno). Per la minimizzazione vincolata, minimax,
goal attainment, e ottimizzazione semi-infinita, sono usati variazioni della
programmazione quadratica sequenziale(SQP).
I problemi Minimi quadrati non lineari usano i metodi di Gauss-Newton e
Levemberg-Marquardt.
Equazioni non lineari si risolvono anche usando l’algoritmo trust-region
dogleg(regione di confidenza) .
Una scelta di strategia di linea di ricerca è data per la minimizzazione non vincolata e
problemi di minimi quadrati .
17
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Le strategie di linea di ricerca usano salvaguardare i metodi di interpolazione
estrapolazione cubica e quadratica .
2.3
Large scale Algorithm
Tutti gli algoritmi su larga scala, eccetto la programmazione lineare, sono metodi
trust-region. I problemi a vincolo limitato ( bound) sono risolti usando i metodi di
newton riflessivo. I vincoli di uguaglianza sono risolti usando un’ iterazione
gradiente coniugato precondizione proiettiva. Puoi utilizzare i risolutori iterativi
sparsi o risolutori diretti sparsi per risolvere sistemi lineari per determinare il passo
corrente. Qualche scelta di precondizione nei risolutori iterativi è anche disponibile.
Il metodo di programmazione lineare è una variante dell’algoritmo di Mehrotra
predictor-corrector, un metodo primale duale interior-point.
L’idea di base dei metodi di “trust region” (“regione di confidenza”) è di
determinare la direzione e l’ampiezza dello spostamento da effettuare a partire
dal punto corrente xk in modo da minimizzare un modello quadratico della
funzione obiettivo in una regione sferica di centro xk.
2.4
Funzioni disponibili
Le tabelle seguenti mostrano le funzioni disponibili per minimizzazione, risoluzione
di equazioni, e la risoluzione di minimi quadrati o problemi di data- fitting.
Le tabelle mostrano una lista dei tipi di problemi in ordine di complessità crescente.
18
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
19
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Per gli algoritmi Standard (o su media-scala) a scopo di esempio verranno utilizzate
le funzioni fminunc, fmincon e fsolve. Le altre routines di ottimizzazione, fgoalattain
fminimax, lsqnonlin, e fseminf, sono utilizzati in maniera quasi identica, con
differenze solo nella formulazione del problema e i criteri di terminazione.
Per quanto riguarda l’ottimizzazione multi obbiettivo è possibile dare diversi esempi
che utilizzano le funzioni lsqnonlin, fminimax, e fgoalattain, includendo come
Simulink può essere usato in combinazione con il toolbox.
Per gli algoritmi su larga scala alcune delle funzioni di ottimizzazione include
algoritmi per problemi di ottimizzazione continua mirati specialmente ai problemi
grandi sparsi o strutture. I principali algoritmi su larga scala sono iterativi, ad
esempio, è generata una sequenza di soluzioni approssimate. In ogni iterazione è
risolto approssimativamente un sistema lineare. I sistemi lineari sono risolti usando
matrici sparse funzionalità di Matlab e una varietà di tecniche di soluzioni lineari
sparse, entrambi iterativi e diretti.
In generale, i metodi di ottimizzazione su larga scala preservano la sparsità e la
struttura, utilizzando informazioni esatte dove possibile. Per risolvere i problemi su
larga scala efficientemente, alcune formulazioni di problemi sono limitate ( come
solo la risoluzione di sistemi sovradeterminati lineari e non lineari) o richiede
informazioni aggiuntive( ad esempio nell’algoritmo di minimizzazione non lineare si
richiede che il gradiente sia fornito in una funzione supplementare fornita
dall’utente).
3. Funzioni in categorie e Input/Output
3.1
Funzioni in categorie
Optimization toolbox prevede queste categorie di funzioni :
Minimizzazione
Funzioni di minimizzazione
Risoluzione di equazioni
Minimi quadrati (Curve Fitting)
Utility
Soluzione di equazioni lineari e non lineari
Curve fitting lineare e non lineare
Settaggio e ritorno dei parametri di ottimizzazione
20
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Minimizzazione
Fgoalattain
Goal attainment multiobbiettivo
Fminbnd
Minimizzazione di scalare non lineare con limite
Fmincon
Minimizzazione vincolata non lineare
Fminimax
Ottimizzazione minimax
Fminsearch,fminunc
Minimizzazione non vincolata non lineare
Fseminf
Minimizzazione semi-infinita
Linprog
Programmazione lineare
Quadprog
Preogrammazione quadratica
Risoluzione di equazioni
\
Usa \ (left division) per risolvere equazioni lineari.
Visits la pagina dei riferimenti degli Operatori Aritmetici nella
documentazione online di Matlab.
Fsolve
Risoluzione di eqauzioni non lineari
Fzero
Risoluzione di equazioni scalari non lineari
Minimi quadrati (Curve Fitting)
\
Lsqlin
Lsqcurvefit
Usa \ (left division) per I minimi quadrati lineari senza vincoli
Vedi pagina dei riferimenti degli Operatori Aritmetici
Minimi quadrati con vicoli lineari
Curve Fitting non lineari
Lsqnonlin
Lsqnonneg
Minimi quadrati non lineari
Minimi quadrati lineari non-negativi
Utility
fzmult
Moltiplicazione con basi nullspace fondamentali
21
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
gangstr
optimget
Zero out “small” entries soggette a grado
strutturale
Ottenere i valori dei parametri delle opzioni di ottimizzazione
optimset
Creare o editare struttura dei parametri di opzioni di ottimizzazione
3.2 Input/Output
Argomenti di Input
Argument
Description
A,b
La matrice A e il vettore b sono, rispettivamente, i
coefficienti dei vincoli di diseguaglianza lineare e il
corrispondente vettore della parte destra : A*x <= b
Aeq,beq
La matrice Aeq e il vettore beq sono, rispettivamente, i
coefficienti dei vincoli di diseguaglianza lineare e il
corrispondente vettore della parte destra : Aeq*x <=
beq
Used by function
fgoalattain,
fmincon, fminimax,
fseminf, linprog,
lsqlin, quadprog
fgoalattain,
fmincon, fminimax,
fseminf, linprog,
lsqlin, quadprog
C,d
La matrice C e il vettore d sono, rispettivamente, i
coefficienti di più o sistemi lineari indeterminati e il
vettore della parte destra da risolvere
f
Il vettore dei coefficienti per il termine lineare
linprog, quadprog
nell’equazione lineare f’ *x o l’eqauzione quadratica x‘
*H* x + f’ *x
fgoalattain,
La funzione da ottimizzare.fun è una funzione o un
fminbnd, fmincon,
oggetto inline.Guarda la funzione sulla pagina di
fminimax,
riferimento per avere maggiori informazioni su fun
fminsearch,
fminunc, fseminf,
fsolve, fzero,
lsqcurvefit,
lsqnonlin
fun
lsqlin, lsqnonneg
goal
Vettori di valori di obbiettivi che si tenta di
raggiungere.Il vettore è della stessa lunghezza del
numero di obbiettivi.
fgoalattain
H
La matrice di coefficienti per i termini quadratici
quadprog
nell’equazione quadratica x’ * H*x+f’*x. H deve essere
simmetrico
lb,ub
Vettori di upper e lower bound( o matrici) .Gli
argomenti sono normalmente della stessa size di
x.Qualche volta se lb ha meno elementi rispetto a x,
fgoalattain,
fmincon, fminimax,
fseminf, linprog,
lsqcurvefit,
22
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
detto m, allora solo i primi m elementi di x sono limitati lsqlin, lsqnonlin,
quadprog
inferiormente;upper bound in ub può essere definito
nello stesso modo.Puoi anche specificare variaibli senza
limiti usando –Inf(per lower bounds) o Inf(per upper
bounds)Per esempio , se lb(i)=-Inf, la variabile x(i) è
non limitata inferiormente .
nonlcon
La funzione che calcola i vincoli di uguaglianza e
diseguaglianza non lineare. Vedi l’unca pagina di
riferimenti per avere maggiori informazioni su nonlcon.
fgoalattain,
fmincon, fminimax
ntheta
Il numero di vincoli semi-infiniti
fseminf
options
Una struttura di parametri di opzioni di ottimizzazione
che definisce parametri usati dalle funzioni di
ottimizzazioni.
All functions
P1,P2….
Argomenti addizionali passati a fun , nonlcon( se esso
esiste), e seminfcon (se esso esiste),quando la funzione
di ottimizzazione chiama le funzioni fun,nonlcon, o
fgoalattain,
fminbnd, fmincon,
fminimax,
fminsearch,
fminunc, fseminf,
fsolve, fzero,
lsqcurvefit,
lsqnonlin
seminfcon usando queste chiamano:
f=feval(fun,x,P1,P2,…)
[c, ceq] = (feval (nonlcon,x,P1,P2,….)
[c,ceq,K1,k2,….,kn,s]=…feval(seminfcon,x,s,P1,P2,…)
Usando questa funzionalità, ka stessa fun( o nonlcon o
seminfcon) può risolvere un numero di problemi simili
con differenti parametri, evitando il bisogno di usare
variabili globali.
seminfcon
La funzione che calcola la diseguaglianza non lineare e
i vincoli di eguaglianza e i vincoli semi-infiniti.
Seminfcon è il nome di un M-file o Mex-file.Vedi le
pagine di riferimento per fseminf per maggiori
informazioni su seminfcon.
fseminf
weight
Un vettore di peso per controlare la relativa sotto
fgoalattain
ottenimento o sopra ottenimento degli obbiettivi
xdata,ydata
L’input xdata e l’output ydata osservato che sono
costruiti dall’equazione
lsqcurvefit
x0
Punto di inizio(uno scalare,una matrice o vettore)
Per fzero ,x0 può anche essere un vettore di due
All functions except
fminbnd
elementi rappresentante un intervall che è noto
contenere uno zero.
x1,x2
L’intervallo sopra cui la funzione è minimizzata
fminbnd
23
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Argomenti di Output
Argument
Description
Used by Functions
attainfactor
Il fattore atteso alla soluzione x
fgoalattain
exitflag
La condizione di uscita.Per il significato di un
All functions
particolare valore, vedi la pagina dei riferimenti
alle funzioni.
fval
Il valore della funzione obbiettivo fun alla
soluzione x
fgoalattain,
fminbnd, fmincon,
fminimax,
fminsearch,
fminunc, fseminf,
fsolve, fzero,
linprog, quadprog
grad
Il valore del gradiente di fun alla soluzione x. Se
fmincon, fminunc
fun non calcola il gradiente, grad è una
approssimazione finita-differenziale del
gradiente
hessian
Il valore dell’hessiano di fun alla soluzione x.
fmincon, fminunc
Per i metodi su larga scala, se fun non calcola
l’hessiano, hessian è un approssimazione finitadifferenziale dell’ Hessiano. Per i metodi su
media scala, hessian è il valore della
approssimazione di Quasi-Newton dell’Hessiano
alla soluzione x.
jacobian
Il valore dello Jacobiano di fun alla soluzione x.
Se fun non calcola lo Jacobiano, jacobian è una
lsqcurvefit,
lsqnonlin, fsolve
approssimazione finita-differenziale dello
Jacobiano.
lambda
Il moltiplicatore di Lagrange alla soluzione x.
Lambda è una struttura dove ogni campo è per
un tipo di vincolo differente. Per la struttura del
campo nome, vedi le descrizioni della funzione
individuale.( Per lsqnonneg, lambda è un
fgoalattain,
fmincon,
fminimax,
fseminf, linprog,
lsqcurvefit,
lsqlin,
lsqnonlin,
lsqnonneg,
24
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
semplice vettore, come lsqnonneg gestisce solo
Data:
30/09/2012
quadprog
un tipo di vincolo).
maxval
Max{fun(x)} alla soluzione x
fminimax
output
La struttura dell’output che contiene
All functions
informazioni circa il risultato di ottimizzazione.
Per la struttura del coampo nome vedi la
descrizione delle singole funzioni.
residual
resnorm
Il valore del residuo alla soluzione x
Il valore del quadrato della norma-2 del residuo
alla soluzione x.
lsqcurvefit,
lsqlin,
lsqnonlin,
lsqnonneg
lsqcurvefit,
lsqlin,
lsqnonlin,
lsqnonneg
x
La soluzione trovata attraverso la funzione di
All functions
ottimizzazione. Se exitflag > 0, allora x è una
soluzione; altrimenti, x è il valore della routine
di ottimizzazione quando esso termina
prematuramente.
25
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
4.
Data:
30/09/2012
Algoritmi Standard
Algoritmi standard fornisce un introduzione alle differenti formulazioni dei
problemi di ottimizzazione e descrive gli algoritmi di media-scala(standard)
usate nelle funzioni del tool. Questi algoritmi sono stati scelti per la loro
robustezza e efficienza iterativa. La scelta della formulazione dei problemi
(non vincolati,minimi quadrati,vincolati) dipende dal problema in esame e
dall’efficienza dell’esecuzione richiesta.
4.1
Gradient methods
I metodi del gradiente sono generalmente molto efficienti quando la funzione
da essere minimizzata è continua nella sua derivata prima.
Metodi di ordine superiore, come il metodo di Newton, sono solo veramente
adatti quando le informazioni di secondo ordine sono prontamente e facilmente
calcolabili, perché calcolare le informazioni di secondo ordine, usando
differenziazione numerica, è computazionalmente costoso.
I metodi del gradiente usano informazioni circa la pendenza della funzione per
dettare una direzione di ricerca dove si ritiene sia il minimo. Il più semplice di
questi è il metodo di discesa ripida(gradiente) in cui viene eseguita una ricerca
in una direzione, -∇f(x), dove ∇f(x) è il gradiente della funzione obbiettivo.
Questo metodo è veramente inefficiente quando la funzione da minimizzare ha
lunghe curvature strette.
4.2 Quasi-Newton Methods
Tra i metodi che usano le informazioni del gradiente, i più favoriti sono i metodi
quasi-Newton. Questi metodi costruiscono informazioni di curvatura ad ogni
iterazione per formulare il problema del modello quadratico della forma:
min (½ x^T )Hx + (c^T)x+b
x
dove la matrice Hessiana, H, è matrice simmetrica definita positiva, c è un vettore
constante, b è una costante. La soluzione ottima per questo problema occorre quando
la derivata parziale di x va a zero, ad esempio,
∇
∗ =
∗+ =0
26
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Il punto della soluzione ottima, x*, può essere scritto come
x* = - (H^-1) c
Il metodo di tipo-Newton (come opposto ai metodi Quasi -Newton) calcola H
direttamente e procede in una direzione di discesa per localizzare il minimo dopo un
numero di iterazioni. Calcolare H numericamente comporta un grande numero di
computazioni. I metodi Quasi -Newton evitano questo usando il comportamento
osservato di f(x) e ∇f(x) per costruire le informazioni di curvatore per fare un
approssimazione di H usando un’ appropriata tecnica di aggiornamento.
Sono stai sviluppati un grande numero di metodi di aggiornamento Hessiano.
Tuttavia si ritiene che il metodo (BFGS) di Broyden, Fletcher, Goldfarb, e Shanno sia
quella di maggiore effetto.
La formula data da BFGS è
=
+
q q
−
q s
Dove
s =
−
q =∇f x
− ∇f x
Come punto di inizio ,
può essere settata ad ogni matrice simmetrica definita
positiva, per esempio la matrice identità I. Per evitare l’inversione dell’Hessiano H,
puoi derivare un metodo di aggiornamento che evita l’inversione diretta di H
attraverso l’uso di una formula che fa un approssimazione dell’Hessiano inverso
ad ogni aggiornamento. Una buona procedura conosciuta è la formula DFP di
Davidon, Fletcher, e Powell. Questo usa la stessa formula come il metodo BFGS
eccetto che èsostituitoda
L’informazione sul gradiente o è fornito calcolando analiticamente i gradienti, o è
derivato attraverso una derivazione parziale usando il metodo della differenziazione
numerica tramite le differenze finite. Questo porta a perturbare le variabili designate,
x, a sua volta e calcolare il tasso di variazione della funzione obbiettivo.
Ad ogni iterazione importante, k, una linea di ricerca è eseguita in direzione
#=−
∗∇
Implementazione Quasi-Newton
27
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Un algoritmo quasi-Newton è usato in fminunc. L’algoritmo consiste di due fasi:
• Determinazione di una direzione di ricerca ( aggiornamento Hessiano)
• Procedure di ricerca di linea
Dettagli sull’implementazione delle due fasi sono discusse sotto.
4.3
Aggiornamento Hessiano
La direzione di ricerca è determinata attraverso la scelta dei metodi BFGS o DFP dati
in “Metodi Quasi-Newton. L’Hessiano, H, è sempre mantenuto definito positivo così
che la direzione di ricerca, d, è sempre in una direzione discendente. Ciò significa che
per qualche arbitrario piccolo passo α nella direzione d, la funzione obbiettivo
decrementa in grandezza.
Raggiungi una definitezza positiva di H garantendo che H è inizializzato ad essere
definito positivo e dopo è sempre positivo. Il termine è prodotto al passo
di linea di ricerca del parametro α e una combinazione di direzione di ricerca d con
la valutazione del passato e presente gradiente,
=α ∇
#−∇
#
Raggiunge sempre la condizione che è positiva attraverso l’esecuzione di una
linea di ricerca sufficientemente accurata. Questo perché la ricerca di direzione, d, è
una direzione discendente, così che α e −∇
# sono sempre positive.Allora il
# che può essere fatto piccolo in grandezza
termine possibile negativo è ∇
come richiesto dall’incremento dell’accuratezza della linea di ricerca.
4.4
Procedure di linea di ricerca
Sono usate due strategie di linea di ricerca, dipende se le informazioni del gradiente
sono facilmente disponibili o se deve utilizzare un metodo di differenza finita.
Quando le informazioni sul gradiente sono disponibili, si usa di default un metodo
polinomiale cubico. Quando le informazioni del gradiente non sono disponibili, si usa
di default una quadratica mista e un metodo polinomiale cubico.
4.5
Ottimizzazione con i minimi quadrati
28
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Le procedure di linea di ricerca usate in congiunzione con un metodo quasi-Newton
sono usati nella funzione fminunc. Essi usano anche parte delle routines per
l’ottimizzazione dei minimi quadrati non lineari, lsqnonlin e lsqcurvefit . Nel
problema dei minimi quadrati una funzione f(x) è minimizzata cioè una somma di
quadrati.
0+1
,-. /
= %&‖
‖(( = ⅀*+
(
(
(3-17)
Problemi di questo tipo occorrono in un largo numero di applicazioni pratiche
specialmente quando le funzioni del modello fitting ai dati, ad esempio , la stima dei
parametri non lineari. Essi sono anche prevalente nel controllo quanto voui un output,
y(x,t), per seguire qualche traiettoria di modello continuo, Ф(t), per il vettore c e lo
scalare t. Questo problema può essere espresso come
0+1 7%
,-. / 27&
3 ,5 −Ф 5
(
#5
(3-18)
Dove y(x,t) e Ф(t) sono funzioni scalari.
Quando l’integrale è discretizzato usando una formula di quadratura adatta, può
essere formulato come un problema di minimi quadrati:
0+1
,-. / = ∑0
+9 3 , 5+ −Ф 5+
(
(3-19)
dove y e Ф includono i pesi dello schema di quadratura. Nota che in questo problema
il vettore F(x) è
3 ,5 −Ф 5
F(x) = 3 , 5( ⋯− Ф 5(
3 , 50 − Ф 50
Nei problemi di questo tipo, il residuo || F(x)|| è probabile essere l’ottimo dato che è
la pratica generale settare la traiettoria dell’obbiettivo realisticamente raggiungibile.
Sebbene la funzione può essere minimizzata usando una tecnica di minimizzazione
non vincolata generale. Il gradiente della matrice Hessiana di LS (Eq.3-18) ha una
struttura speciale.
29
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Denotando la matrice Jacobiana m per n di F(x) come J(x), il vettore gradiente di F(x)
come G(x), la matrice Hessiana di F(x) come H(x), e la matrice Hessiana di ogni
*+
, ℎ<=
+
G(x) =2J
>
+ 2@
(3-20)
Dove
Q(x) =∑0
+
+9 *+
La matrice Q(x) ha la proprietà che quando il residuo ||F(x)|| tende a zero come
approccia alla soluzione, allora Q(x) anche tende a zero. Allora quando ||F(x)|| è
piccolo alla soluzione, un metodo veramente effettivo è usare la direzione di GaussNewton come base per una procedura di ottimizzazione.
4.6
Metodo Gauss-Newton
Nel metodo di Gauss-Newton, una direzione di ricerca, # è ottenuta ad ogni
iterazione importante k, cioè una soluzione del problema dei minimi quadrati.
La direzione derivata da questo metodo è equivalente alla direzione di newton
quando il termine di Q(x) può essere ignorato. La direzione di ricerca # può essere
utilizzata come parte di una strategia di ricerca di linea per garantire che ad ogni
iterazione la funzione f(x) decrementa.
Consideriamo le efficienze che sono possibili con il metodo di Gauss-Newton. La
figura sottostante mostra il cammino verso il minimo sulla funzione di Rosembrock
quando posto il problema dei minimi quadrati. Il metodo di Gauss-Newton converge
solo dopo 48 valutazione di funzione usando gradienti a differenza finita, comparato
a 140 iterazioni usando un metodo BFGS non vincolato.
Il metodo di Gauss-newton spesso incontra problemi quando il termine di secondo
ordine nell’equazione 3-20 è significativo. Il metodo che supera questo problema è il
metodo di Levemberg-Marquardt.
30
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
4.7
Data:
30/09/2012
Metodo di Levemberg-Marquardt
Il metodo di Levemberg-Marquardt usa una direzione di ricerca cioè una soluzione di
un insieme lineare di equazioni
Dove lo scalareA controlla entrambi la grandezza e la direzione di # .Quando A è
zero, la direzione # è identica a ciò del metodo di Gauss-Newton. Come A tende a
infinito, # , tende verso un vettore di zero e una direzioen steepest discent. Questo
implica che per A sufficientemente grande, il termine *
+# B*
vale
vero. Il termine A può quindi essere controllato per garantire discesa anche quanto
termini di secondo ordine , che restringono l’efficienza di Gauss Newton , sono
incontrati.
Il metodo di Levemberg-Marquardt quindi usa una direzione di ricerca che è un
incrocio tra la direzione di Gauss –Newton e steepest descent. Questo è illustrato
nella figura sottostante, il metodo di Levemberg-Marquardt sulla funzione di
Rosembrock. La soluzione per la funzione di Rosembrock converge dopo 90
valutazioni di funzione comparate alle 48 del metodo di Gauss-newton. La povertà di
efficienza è in parte per il metodo di Gauss-Newton è generalmente più efficace
quando il residuo è zero alla soluzione. Spesso, qualche informazione non è sempre
31
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
disponibile in anticipo, e l’incremento robusto del metodo di Levemberg-Marquardt
compensa per le sue occasionali mancanze di efficienza.
4.8
Implementazione minimi quadrati non lineari
Sia il metodo di Gauss-Newton che il metodo di Levemberg-Marquardt sono
implementati nel Optimization Toolbox. Dettagli sulle implementazioni sono discussi
in questa sezione:
- Implementazione di Gauss- Newton;
- Implementazione di Levemberg-Marquardt;
Implementazione di Gauss – Newton
Il metodo di Gauss-Newton è implementato usando strategie di linea di ricerca
polinomiale simili a quelle discusse per ottimizzazione non vincolata. Per la
soluzione del problema dei minimi quadrati, puoi evitare peggioramenti del
condizionamento delle equazioni usando la decomposizione QR di J(
e
applicando la decomposizione a F(
(usando l’operatore \ di MTLAB). Questo è in
>
, questo può causare
contrasto all’inversione della matrice esplicita, >
errori inutili.
32
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Sono include misure robuste nel metodo. Queste misure consiste di scambio
dell’algoritmo con il metodo di Levemberg-Marquardt quando sia quando la
lunghezza del passo va oltre ad un valore soglia, o quando il numero di condizione di
J(
è il seguente 1e-10. Il numero di condizione è il rapporto tra il singolo valore
più grande e quello più piccolo.
Implementazione di Levemberg-Marquardt
La difficoltà principale dell’implementazione del metodo di Levemberg-Marquardt è
una strategia effettiva per controllare la grandezza di A ad ogni iterazione così che
esso è efficiente per un ambio raggio di problemi. Il metodo usato in questa
implementazione è stimare la relativa non linearità di f(x) usando una predetta lineare
somma di quadrati C
e una interpolazione cubica stima del minimo
∗ . In
questo modo la grandezza di A è determinata ad ogni iterazione.
La somma di quadrati lineare predetta è calcolata come
C
=>
#
+*
e il termine C
è ottenuto un interpolazione a cellette del punto f
e
.
Un parametro per la lunghezza del passo <∗ è ottenuto anche con questa
interpolazione, che è il passo stimato per il minimo. Se, C
è più grande rispetto a
∗ , allora A si riduce , altrimenti è incrementato. La giustificazione per questo è
e
la differenza tra C
∗ è una misura dell’efficacia del metodo di GaussNewton e della linearità del problema. Questo determina se usare una direzione per
approcciare con la direzione steepest descent o la direzione Gauss-Newton. Le
formula per la riduzione e l’incremento di A ,che è stato sviluppato attraverso un
largo numero di problemi di test, sono mostrati nella figura seguente.
33
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Aggiornamento di A
L’implementazione è stata con successo testata su un grande numero di problemi non
lineari. Esso ha provato che è più robusto rispetto il metodo di Gauss-Newton e
iterativamente più efficiente rispetto un metodo non vincolato. L’algoritmo
Levemberg-Marquardt è il metodo di default usato da lsqnon lin. Puoi selezionare il
metodo di Gauss-Newton , settando parametro di options ‘LevembergMarquardt a
‘off’.
5 Algoritmi su larga scala
5.1
Metodi Trust-Region per minimizzazione non lineare
Molti dei metodi usati in Optimization Toolbox sono basati su trust – region,
un semplice ma potente concetto di ottimizzazione.
Per capire l’approccio trust – region all’ottimizzazione, consideriamo un
problema di minimizzazione non vincolato, minimizza f(x), dove la funzione
prende un vettore di argomenti e ritorna uno scalare. Supponiamo che sei in un
punto x in uno spazio n e vuoi migliorare, ad esempio, muovere in un punto
con un valore di funzione inferiore. L’idea di base è di approssimare f con una
34
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
semplice funzione q, che riflette adeguatamente il comportamento della
funzione f in un vicino N intorno al punto x. Questo vicino è detto trust region.
Un passo di prova s è calcolato attraverso la minimizzazione (o
minimizzazione approssimata) su N. Questo è un sotto problema trust-region,
0+1
FG
H{
Il punto corrente è aggiornato per essere x + s se f(x + s) < f(x); altrimenti altrimenti
il punto corrente rimane inalterato e N, la regione di fiducia (trust), è ridotta e il passo
di prova viene ripetuto.
Le questioni chiave nel definire una specifica trust-region per minimizzare f(x) sono
come scegliere e calcolare l ‘approssimazione q (definita al punto corrente x), come
scegliere e modificare la trust region N, e come risolvere accuratamente il
sottoproblema di trust region.
Nel metodo standard di trust region, l’approssimazione quadratica q è definita dai
primi due termini dell’approssimazione di Taylor da f a x; la regio N è usualmente
sferica o ellissoidale nella forma. Matematicamente il sottoproblema trust-region è
tipicamente dichiarato:
minI
(
+
J5<KL ℎL‖MH ‖ ≤ ∆P
Dove g è il gradiente di f al punto corrente x, H è la matrice Hessian(la matrice
simmetrica di derivata seconda), D è una matrice diagonale, ∆ è uno scalare positivo,
||.|| è la norma 2. Buoni algoritmi esiste per risolvere l’equazione sopra scritta; tali
algoritmi tipicamente risolvono la computazione ti un sistema caratteristico pieno e
un processo di Newton applicato a un equazione secolare.
1
1
−
=0
∆ ‖ ‖
Questi algoritmi trovano una soluzione accurata all’equazione. Qualche volta, essi
richiedono tempo proporzionale per alcune fattorizzazioni di H. Quindi per i
problemi su larga scala c’è bisogno di un approccio differente. Alcune
approssimazioni e strategie euristiche, basate sull’equazione precedente sono state
proposte in letteratura. L’approccio di ottimizzazione seguito da Optimization
Toolbox è di restringere il sottoproblema del trust-region in un sottospazio due dimensionale S. Una volta che il sottospazio è calcolato il lavoro per risolvere
l’equazione sopra descritta è banale anche se c’è bisogno di avere tutte le
informazioni sugli auto valori e auto vettori. Il lavoro dominante è ora spostato nella
determinazione del sottospazio.
Il sottospazio due dimensionale S è calcolato con l’aiuto di un processo del gradiene
coniugato precondizionato descritto di seguito. Il toolbox assegna S = <s1,s2>, dove
s1 è nella direzione del gradiente g , e s2 è una direzione di Newton approssimata, ad
esempio, una soluzione a
35
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
H * ( = -g
O una direzione di curvatura negativa,
∗ ( B0
( ∗
La filosofia dietro questa scelta di S è forzare la convergenza globale( attraverso la
direzione di steepest discent o direzione di curvatura negativa) e raggiungere una
convergenza locale ( con il passo di Newton , se esso esiste).
Un frame work per Optimization Toolbox per minimizzazione non vincolata usando
trust-region è ora facile da descrivere:
4. Formulare il sottoproblema trust-region due dimensionale.
5. Risolvere l’equazione sopra descritta per determinare il passo di
prova s.
6. Se f((x +s)) <=f(x)) allora x = x +s.
7. Aggiustare ∆.
Questi quattro passi sono ripetuti fino alla convegenza. La dimensione ∆ della trustregion è regolata in accord con le regole standard. In particolare , essa è decrementata
se il passo di prova non è accettato , ad esempio f(x + s) >= f(x).
5.2 Gradienti Coniugati Precondizionati
Una strada diffusa per risolvere grandi sistemi definiti positivi simmetrici di
equazioni lineari Hp = -g è il metodo dei Preconditioned Conjugate Gradients
(PCG). Questo approccio iterativo richiede l’abilità di calcolare il prodotto matrice –
vettore della forma H * v dove v è un vettore arbitrario. La matrice definita positiva
R è una matrice
simmetrica M è una precondizione per H. Cioè, M = R ( dove R
buon condizionata o una matrice con auto valori raggruppati (cluster)
Algoritmo
The Optimization Toolbox uses this PCG algorithm, which it refers to as
Algorithm PCG.
% Initializations
r = -g; p = zeros(n,1);
% Precondition
z = M\r; inner1 = r'*z; inner2 = 0; d = z;
% Conjugate gradient iteration
for k = 1:kmax
if k > 1
beta = inner1/inner2;
d = z + beta*d;
end
w = H*d; denom = d'*w;
if denom <= 0
p = d/norm(d); % Direction of negative/zero curvature
36
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
break % Exit if zero/negative curvature detected
else
alpha = inner1/denom;
p = p + alpha*d;
r = r - alpha*w;
end
z = M\r;
if norm(z) <= tol % Exit if Hp=-g solved within tolerance
break
end
inner2 = inner1;
inner1 = r'*z;
end
In un contesto di minimizzazione , puoi assumere che la matrice Hessiana H è
simmetrica. Tuttavia, H è garantita essere definita positiva solo nella vicinanza di una
forte minimizzatore. L’algoritmo PCG esiste quando una direzione di curvature
negative ( o zero) è incontrata, ad esempio, # # ≤ 0. L direzione dell’output del
PCG, p, è una direzione di curvatura negativa o un soluzione approssimata del
sistema di Newton Hp = -g. In entrambi i casi p è usato per aiutare a definire il
sottostazione due dimensionale usato nell’approccio trust-region.
5.3 Minimi quadrati non lineari
Un importante caso speciale per f(x) è il problema dei minimi quadrati non lineari
Dove F(x) è una funzione vettore – valutata con componente i di F(x) uguale a + .
Il metodo di base usato per risolvere questo problema è lo stesso come nel caso
generale descritto nella parte di Trust Region. Tuttavia la struttura del problema dei
minimi quadrati non lineari è sfruttata per migliorare l’efficienza. In particolare, un
direzione Gauss-Newton approssimata, ad esempio, una soluzione a s a
min‖>H *‖((
dove J è lo Jacobiano di F(x) , è usato a definire il sottospazio due dimensionale S. Le
derivate seconde della componente della funzione + (x) non sono usate.
In ogni iterazione il metodo dei gradienti coniugati precondizionati è usato per
risolvere approssimativamente l’equazione normale, ad esempio,
> >H
> *
Sebbene le equazioni normali non sono esplicitamente formate.
37
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
5.4 Minimi quadrati lineari
In questo caso la funzione da risolvere è
f(x) = ‖R + #‖((
(
L’algoritmo genera iterazioni convergenti fattibili, nel limite, ad una soluzione locale.
Ogni iterazione implica la soluzione approssimata di un sistema lineare grande (di
ordine n dove n è la lunghezza di x). Le matrici di iterazione hanno la struttura della
matrice C. In particolare, il metodo dei gradienti coniugati precondizionati è usato per
risolvere approssimativamente l’equazione normale, ad esempio,
R R = −R #
Sebbene l’equazione normale non è formata esplicitamente.
Il sottospazio del metodo trust-region è usato per determinare una direzione di
ricerca. Qualche volta, invece di restringere il passo ad un possibile passo riflesso,
come nel caso della minimizzazione non lineare, è condotto una linea di ricerca
riflessiva a tratti ad ogni iterazione, come nel caso quadratico. In definitiva, il sistema
lineare rappresenta un approccio di Newton catturando le condizioni di ottimalità di
primo ordine alla soluzione, risultando un tasso di convergenza forte locale.
6 My functions ( qualche funzione in dettaglio )
6.1
Minimizzazione non vincolata non lineare
Fminsearch
Scopo
Trova il minimo di una funzione non vincolata multi variabile
0+1
,
Dove x è un vettore e f(x) è una funzione che ritorna uno scalare.
Descrizione
38
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
[x,fval,exitflag,output] = fminsearch(fun,x0,options,P1,P2,…)
La funzione fminsearch trova un minimo di una funzione scalare di qualche
variabile, partendo da una stima iniziale. Questo è generalmente riferito
all’ottimizzazione non vincolata non lineare.
Comincia nel punto x0 e trova un minimo locale x della funzione descritta in
fun, x0 può essere uno scalare , un vettore, o una matrice.
Utilizzando options, minimizza con i parametri di ottimizzazione specificati
nella struttura options. Usa optimset per settare i parametri.
E’ possibile passare dei parametri da cui il problema è dipendente ,P1,P2,etc.
direttamente alla funzione fun.
Ritorna in fval il valore della funzione obbiettivo fun alla soluzione x.
Ritorna un valore exitflag che descrive la condizione di uscita di fminsearch.
> 0 La funzione converge ad una soluzione x
0
Il massimo numero di valutazioni di funzione o iterazioni è eccesso
< 0 La funzione non converge a nessuna soluzione
Ritorna una struttura di output che contiene informazioni circa l’ottimizzazione
• Iterations: numero di iterazioni fatte
• funcCount: numero di funzioni valutate
• algorithm : algoritmo usato
Algoritmi
Fminsearch usa il metodo di ricerca del simplesso. Questo è un metodo di
ricerca diretta che non usa gradienti numerici o analitici come fminunc.
Se n è la lunghezza di x, un simplesso in uno spazio n-dimensionale è
caratterizzato da n+1 vettori distinti che sono i suoi vertici. In uno spazio di
grandezza due , un simplesso è un triangolo; in spazio tre , è una piramide. Ad
ogni passo della ricerca, un nuovo punto dentro o vicino al simplesso corrente
è generato. Il valore della funzione nel nuovo punto è comparata con il valore
della funzione al vertice del simplesso e , usualmente, uno dei vertici è
rimpiazzato dal nuovo punto, dando un nuovo simplesso. Questo passo è
ripetuto fino a che il diametro del simplesso è meno della tolleranza
specificata.
39
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
fminsearch è generalmente meno efficiente rispetto fminunc per il problema di
ordine maggiore di due. Qualche volta , quando il problema è altamente
discontinuo, fminsearch potrebbe essere più robusto.
fminsearch spesso può gestire discontinuità, particolarmente se essa non
occorre vicino alla soluzione. fminsearch potrebbe solo dare una soluzione
locale.
fminsearch minimizza solo sui numeri reali, cioè, x deve consistere solo di
numeri reali e f(x) deve ritornare numeri reali. Quando x ha variabili
complesse, esse devono essere divisi in parti reali ed immaginarie.
Fminunc
Scopo
Trova il minimo di una funzione multi variabile non vincolata
0+1
,
Dove x è un vettore e f(x) è una funzione che ritorna uno scalare.
Descrizione
[x, fval, exitflag, output, grad, hessian]= fminunc(fun, x0, options, P1, P2,…);
Fminunc trova il minimo di una funzione scalare di diverse variabili, partendo
da una stima iniziale. Questo generalmente è riferito all’ ottimizzazione non
vincolata non lineare.
Tutti i parametri in input e output seguono la stessa descrizione di fminsearch
tranne per :
grad è il valore del gradiente di fun alla soluzione x;
hessian è il valore dell’Hessiano della funzione obbiettivo fun alla soluzione x.
Nota
fminunc non è preferito come scelta per la risoluzione di problemi che sono la
somma di quadrati, cioè, della forma:
min f(x)=
(
+
(
(
+
S
(
+T
40
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Invece si usa la funzione lsqnonlin, con cui si ottimizza problemi di questa
forma.
Per usare il metodo su larga-scala, devi prevedere il gradiente in fun( e settare
il parametro GradObj a ‘on’ usando optimset). Un errore è dato se il gradiente
non è previsto e il parametro LargeScale non è ‘off’.
Algoritmi
Di default fminunc sceglie l’algoritmo su larga-scala se l’utente fornisce il
gradiente in fun. Questo algoritmo è una sottospecie del metodo trust region e è
basato sul metodo di Newton riflessivo interiore. Ogni interazione implica una
soluzione approssimata di un sistema lineare largo usando il metodo di
precondizione dei gradienti coniugati
Fminunc, con il parametro LargeScale settato a off con optimset, usa il metodo
quasi-Newton BFGS con le procedure di ricerca di linea mixed-quadratic e
cubic line. Questo metodo quasi-Newton usa la formula BFGS per aggiornare
l’approssimazione della matrice Hessiana. Puoi selezionare la formula DFP,
con cui si approssima la matrice Hessiana inversa, settando il parametro
HessUpdate a ‘dfp’. Puoi selezionare il metodo steepest descent settando
HessUpdate a ‘steepdesc’, sebbene questo non è raccomandato.
La funzione da minimizzare deve essere continua. Fminunc può solo dare una
soluzione locale. fminunc minimizza solo su numeri reali , cioè, x deve
consistere di numeri reali e f(x) deve ritornare numeri reali. Quando x ha
variaibli complesse, esse si dividono in parti reali e immaginarie.
6.2
Minimi quadrati lineari e non lineari
Lsqlin
Scopo
Risolve il problema dei minimi quadrati
UVW ,(
‖R − #‖( 5<KL ℎL A*x<=b
Aeq * x =beq
Lb<=x<=ub
Dove C,A, e Aeq sono matrici e d, b, beq, lb, ub, e x sono vettori.
41
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Descrizione
[x, resnorm, residual, exitflag, output, lambda]= lsqlin(C, d, A, b, Aeq, beq, lb,
ub, x0, options, p1, p2, …);
Risolve un sistema lineare C*x=d nel senso dei minimi quadrati soggetto a
A* x <= b, dove C è una matrice m*n.
Aeq*x=beq è un addizionale vincolo di uguaglianza da soddisfare. Settare
A=[] e b=[] se non esiste la diseguaglianza.
Si definisce un lower e un upper bound sulle variabili designate in x così che la
soluzione è sempre compresa lb<= x <= ub. Settare Aeq=[] e beq=[] se non
esiste l’uguaglianza
Settare il punto di inizio in x0. Setta lb=[] e b=[] se non esistono limiti.
Minimizza con i parametri di ottimizzazione specificati attraverso la struttura
options. Usare optimset per settare questi parametri.
Si possono passare i parametri p1, p2 problema-dipendenti direttamente della
funzione multipla Jacobiana se essi esistono . Specifica la funzione multipla
Jacobiana usando il parametro di options JacobMult.
Ritorna il valore del quadrato norma 2 del residuo, norm(C*x-d)^2.
Ritorna residual C*x-d.
Ritorna il valore exitflag che descrive la condizione di uscita.
• > 0 La funzione converge alla soluzione x.
• 0
Il massimo numero di valutazioni di funzione o iterazione è stato
superato
• < 0 La funzione non converge a nessuna soluzione
Ritorna una struttura di output che contiene informazioni circa l’ottimizzazione
• Iterations
• Algorithm
• Cgiterations
scala)
• Firstorderopt
numero di iterazioni fatte
Algoritmo usato
numero di iterazioni PCG( solo algoritmi su larga
significato di ottimalità di primo ordine
42
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Ritorna una struttura lambda i cui campi contengono i moltiplicatori di Lagrange.
•
•
•
•
Lower
Upper
Ineqlin
Eqlin
lower bonds lb
upper bond ub
diseguaglianza lineare
uguaglianza lineare
Algoritmo
Quando il problema dato a lsqlin ha solo upper e lower bound; ad esempio, non sono
specificate diseguaglianze o uguaglianze lineari, e la matrice C ha almeno tante righe
quante sono le colonne, l’algoritmo di default è un metodo su larga scala. Questo
metodo è una sottospecie del metodo trust region basato sul metodo di Newton
interiore- riflessivo. Ogni iterazione comporta la soluzione approssimata di un
sistema lineare largo usando il metodo di precondizione dei gradienti
coniugati(PCG).
Lsqlin, con il parmetro LargeScale settato ad ‘off’ con optimset, o quando sono date
diseguaglianze o uguaglianze lineari, è basato su programmazione quadratica, il
quale usa un metodo di insieme attivo. Esso trova una possibile soluzione iniziale
risolvendo un problema di programmazione lineare.
Note
Il metodo su larga scala non permette che upper e lower bond siano uguali. Per
esempio if lb(2) = = ub(2), then lsqlin da errore.
Equal upper and lower bond not permitted in this large-scale method.
Use equality constraints and the medium-scale method instead.
A questo punto devi usare l’algoritmo su media scala per risolvere il problema di
uguaglianza di vincoli.
Per quanto riguarda l’ottimizzazione su media scala, se le matrici C,A, o Aeq sono
sparse, e la formulazione del problema non è risolvibile usando il metodo su larga
scala, lsqlin da errore e indica che le matrici siano convertite a pieno.
Warning:this problema formulation not yet available for sparse matrices.
Converting to full to solve.
Quando il problema non è fattibile, lsqlin da questo errore:
43
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Warning: The constraints are overly stringent;
There is no feasible solution;
In questo caso lsqlin, produce un risultato che minimizza la violazione dei vincoli del
caso pessimo.
Quando i vincoli di uguaglianza sono inconsistenti. Lsqlin da:
Warning: The equality constraints are overly stringent;
There is no feasible solution.
In questo momento, gli unici livelli di display, usando I parametri di Display in
options, sono ‘off’ e ‘ final’; output iterativo usando ‘iter’ non è disponibile.
Lsqnonlin
Scopo
Risolve problemi dei minimi quadrati non lineari (data-fitting non lineari).
0+1
,
X
Y=
(
+
(
(
+
(
S
+ ⋯+
0
(
+T
Dove L è una costante
Descrizione
Lsqnonlin risolve problemi dei minimi quadrati non lineari, includendo problemi di
data-fitting non lineari.
Piuttosto che risolvere il valore di f(x) (la somma dei quadrati), lsqnonlin richiede la
funzione user-defined per calcolare la funzione vector-valued.
F(x) =
(
S
Dopo , nei termine dei vettori, si può riformulare il problema di ottimizzazione come
0+1
1
||*
,2
||(( = ⅀
+
(
44
Tesina di Ottimizzazione, 2011/2012
Optimization toolbox
Data:
30/09/2012
Dove x è un vettore e F(x) è una funzione che ritorna un valore del vettore.
[x, resnorm, residual, exitflag, output, lambda, jacobian] = lsqnonlin
(fun,x0,lb,ub,options,P1,P2,…);
Jacobian ritorna lo Jacobiano di fun alla soluzione x;
Il resto dei valori di input e output seguono la descrizione di lsqlin.
Algorithm
Di default lsqnonlin sceglie un algoritmo su larga scala. Questo algoritmo è una
sottospecie del metodo trust-region e si basa sul metodo di Newton interioreriflessivo. Ogni iterazione riporta una soluzione approssimata di un sistema lineare
largo usando il metodo dei gradienti coniugati precondizionati (PCG).
Se vuoi settare il parametro ‘LargeScale’ a ‘off’ con optimset, lsqnonlin usa il
metodo di Levenberg-Marquardt con ricerca di linea. Alternativamente , puoi
selezionare il metodo di Gauss-Newton con ricerca di linea settando il parametro
LevembergMarqaurdt. Settando LevembergMarquardt (e LargeScale a ‘off’) si
selezione il metodo Gauss-Newton che è generalmente più veloce quando il residuo
||* ||(( è piccolo.
L’algoritmo di ricerca di linea di Default, ad esempio, il parametro LineSearchType
settato a ‘quadcubic’, è un metodo safeguarded quadratico misto e interpolazione e
estrapolazione polinomiale cubica. Puoi selezionare un metodo safeguarded
polinomiale cubico settando il parametro LineSearchType a ‘cubicpoly’. Questo
metodo generalmente richiede poche valutazioni di funzione ma molte valutazione di
gradiente. Allora , se i gradienti sono supportati e possono essere calcolati
velocemente, il metodo polinomiale cubico di ricerca di linea è preferibile.
La funzione da minimizzare deve essere continua, lsqnonlin può solo dare una
soluzione locale.
Gestisce solo varabili reali, quando x ha variabili complesse, le variabili devono
essere scisse in due parti reali e immaginarie.
45