Note - DISMA Dipartimento di Scienze Matematiche

Politecnico di Torino
Corso di Laurea in Matematica per le Scienze dell’Ingegneria
Dipartimento di Matematica
Seminari MAT+
Mercoledı̀ 19 marzo 2008
Numeri complessi: trigonometria con e senza la H
Marco Codegone
Sommario
Inquesto seminario desidero presentare i numeri complessi nelle loro varie forme e in particolare
nella forma esponenziale, per ricaverne alcune proprietà importanti riguardanti il modulo e l’argomento, le potenze e il logaritmo. Si presenterà poi l’estenzione delle funzioni trigonometriche
ai numeri complessi, mostrando come le formule della trigonometria sono riconducibili alle prorpietà dell’esponenziale complesso. In questo quadro le funzioni iperboliche godono di analoghe
propprietà.
1
Forma cartesiana
Il primo modo di presentare i numeri complessi z ∈ C è quello di identificarli a un coppia ordinata
di numeri reali:
z ∈ C ⇐⇒ z = {(x, y) ∈ R2 , x ∈ R, y ∈ R}
Quindi z ∈ C può essere identificato a un punto del piano o a un vettore del piano. Le operazioni
binarie di somma e prodotto di due numeri complessi z = (x, y) e w = (a, b) sono definite nel
modo segunete:
z + w = (x + a, y + b)
z · w = (xa − yb, xb + ya)
Lo zero complesso è il numero (0, 0) e l’unità complessa è il numero (1, 0). Si può provare che
C, con queste operazioni, è un campo. Nel campo complesso trova soluzione l’equazione:
z 2 + (1, 0) = (0, 0)
infatti il numero complesso z = (0, 1) è tale che
z 2 = (0, 1) · (0, 1) = (0 · 0 − 1 · 1, 0 · 1 + 1 · 0) = (−1, 0).
Si introduce inoltre il concetto di modulo |z| e di argomento arg z di un numero complesso
z = (x, y):
p
|z| = x2 + y 2
(1)
1
¡ ¢

arctan ¡ xy ¢




arctan ¡ xy ¢ + π



arctan xy − π
arg z =
π


2



− π2


non è definito
se
se
se
se
se
se
x>0
x<0
x<0
x=0
x=0
x=0
e
e
e
e
e
y
y
y
y
y
≥0
<0
>0
<0
= 0.
(2)
L’argomento cosı̀ definito è unico. Tuttavia si osserva facilmente che esso rappresenta un angolo
che la semiretta dell’asse delle x positive forma con la semiretta su cui giace il segmento che
congiunge l’origine degli assi con z. Dunque se noi aggiungiamo 2kπ, con k ∈ Z, ad arg z
otteniamo sempre lo stesso numero complesso.
2
Forma matriciale
Un altro modo di presentare i numeri complessi è quello di edentificarli alle matrici quadrate
2 × 2 di un opportuno tipo nel modo seguente:
µ
¶
x −y
z=
y x
con x ∈ R e y ∈ R. Le operazioni di somma e prodotto sono le oparazioni di somma e prodotto
di matrici. Siano:
µ
¶
µ
¶
x −y
a −b
z=
w=
y x
b a
si ha:
µ
¶ µ
¶ µ
¶
x −y
a −b
x + a −(y + b)
z+w =
+
=
y x
b a
y+b
x+a
µ
¶ µ
¶ µ
¶
x −y
a −b
x · a − y · b −(x · b + y · a)
z·w =
·
=
y x
b a
x·b+y·a
x·a−y·b
Lo zero complesso è la matrice
µ
0 0
0 0
¶
mentre l’unità complessa è la matrice:
µ
L’equazione:
µ
2
z +
1 0
0 1
ha la soluzione:
µ
z=
infatti:
1 0
0 1
µ
0 −1
1 0
¶
¶
.
µ
=
0 −1
1 0
0 0
0 0
¶
¶
¶ µ
¶ µ
¶
0 −1
−1 0
·
=
.
1 0
0 −1
2
Il modulo del numero complesso è dato dalla radice quadrata del determinante:
s
µ
¶ p
x −y
|z| = det
= x2 + y 2 .
y x
La corrispondenza tra la rappresentazione di C come punti del piano e quella sotto forma di
matrici è la seguente:
µ
¶
x −y
z = (x, y) ←→ z =
.
y x
3
Forma cartesiana con la i
Un modo molto comune di presentare un numero complesso z è quello di idendificarlo a una
coppia ordinata di numeri reali x e y secondo l’espressione x + i y. La somma e il prodotto di
due numeri complessi z = x + i y e w = a + i b è definita nel modo seguente:
z = (x + i y) + (a + i b) = (x + a) + i (y + b)
z = (x + i y) · (a + i b) = (x · a − y · b) + i (x · b + y · a)
Si osservi come in queste operazioni i è stato trattato come se fosse un versore e viene detto
unità immaginaria è gode della proprietà che:
i 2 = −1.
Lo zero complesso è il numero z = 0 + i 0 = 0 e l’unità complessa è il numero z = 1 + i 0 = 1.
Si può provare che C, con queste operazioni, è un campo. Nel campo complesso trova soluzione
l’equazione:
z2 + 1 = 0
infatti il numero complesso z = i è tale che
(0 + i ) · (0 + i ) = i · i = −1 + i 0 = −1.
La corrispondenza tra la rappresentazione di C come punti del piano, quella sotto forma di
matrici e quella con unità immaginaria è la seguente:
µ
¶
x −y
z = (x, y) ←→ z =
←→ z = x + i y.
y x
4
Forma polare trigonometrica
Un altro modo molto comune di presentare un numero complesso z = x + i y è quello di idendificare la sua parte reale x e la sua parte immaginaria y utilizzando le coordinate polari r = |z|
e θ = arg z come definite nelle formule (1) e (2):
z = r(cos θ + i sin θ)
si osservi che la coordinata θ non è unica, ma si ha anche:
z = r(cos(θ + 2kπ) + i sin(θ + 2kπ))
3
con
k∈Z
La somma di due numeri complessi z = r(cos θ + i sin θ) e w = ρ(cos φ + i sin φ) è definita con la
regola del parallelogramma e non precisiamo oltre i dettagli. E’ invece interessante approfondire
il prodotto di z = r(cos θ + i sin θ) e w = ρ(cos φ + i sin φ):
z = r(cos θ + i sin θ) · ρ(cos φ + i sin φ) =
= rρ ((cos θ · cos φ − sin θ · sin φ) + i (cos θ · sin φ + sin θ · cos φ))
Ora per le formule di somma e sottrazione della trigonometria si ha:
rρ (cos θ · cos φ − sin θ · sin φ) + i
|
{z
}
=
cos(θ + φ)
+i
(cos θ · sin φ + sin θ · cos φ) =
|
{z
}
sin(θ + φ)
dunque per fare il prodotto di due numeri complessi si moltiplicano i moduli e si sommano gli
argomenti. Si osserva dunque facilmente che se i numeri complessi hanno modulo unitario il
loro prodotto si trasforma in una somma degli argomenti. Questo fatto dà intuitivamente una
giustificazione alla formula di Eulero:
e i θ = cos θ + i sin θ
con
θ ∈ R.
(3)
Anzi possiamo dire che una volta accettata la formula di Eularo da essa seguono le formule di
somma e sottrazione della trigonometria:
e iθ · e iφ =
= (cos θ · cos φ − sin θ · sin φ) + i
{z
}
|
=
cos(θ + φ)
+i
i
(θ+φ)
= e
.
5
(cos θ · sin φ + sin θ · cos φ) =
|
{z
}
sin(θ + φ)
Forma esponenziale
Il modo per noi più interessante di esprimere un numero complesso z è quello di esprimerlo nella
sua forma esponenziale:
z = r e iθ
ove r è il modulo di z e θ è l’argomento di z come sono stati definiti nelle formule (1) e (2). La
corrispondenza tra la rappresentazione di C come punti del piano, quella sotto forma di matrici
e quella con unità immaginaria è la seguente:
µ
¶
x −y
z = (x, y)
←→ z =
←→
y x
←→ z = x + i y ←→ z = r(cos θ + i sin θ) ←→ z = r e i θ ,
ove i legami tra r e θ con x e y sono dati dalle formule (1) e (2) e dalle espressioni seguenti:
½
x = r cos θ
y = r sin θ.
4
6
Alcune proprietà del modulo e dell’argomento
La forma esponenziale complessa permette di ricavare in modo particolarmente semplice le
proprietà del modulo e dell’argomento.
Siano
z1 = ρ1 e i ϑ1 ,
z2 = ρ2 e i ϑ2 .
a)
Si ha:
z1 z2 = ρ1 e i ϑ1 ρ2 e i ϑ2 = ρ1 ρ2 e i (ϑ1 +ϑ2 )
e quindi:
|z1 z2 |
= |ρ1 ρ¡2 e i (ϑ1 +ϑ2 ) | ¢ = ρ1 ρ2 ,
arg z1 z2 = arg ρ1 ρ2 e i (ϑ1 +ϑ2 ) = ϑ1 + ϑ2 .
b)
Si ha:
z1
ρ1 e i ϑ1
ρ1 i (ϑ1 −ϑ2 )
=
=
e
,
i ϑ2
z2
ρ
ρ2 e
2
e quindi:
c)
¯ ¯
¯ z1 ¯
¯ z2 ¯
arg zz12
¯
¯
¯ρ
¯
ρ
= ¯ ρ12 e i (ϑ1 −ϑ2 ) ¯
= ρ12 ,
³
´
ρ
= arg ρ12 e i (ϑ1 −ϑ2 )
= ϑ1 − ϑ2 .
Osserviamo infine che la moltiplicazione per un esponenziale con all’esponente un immaginario puro provoca una rotazione:
¡
¢
arg z1 e i α = α + arg z1 .
In particolare la moltiplicazione per i provoca una rotazione di π/2:
arg ( i z1 ) =
π
+ arg z1 .
2
In modo analogo si osserva che che la moltiplicazione per i n provoca una rotazione di
nπ/2 e in particolare :
i 4n z = z,
i 4n−1 z = − i z,
i 4n−2 z = −z,
i 4n−3 z = i z.
Esempio 1 Si determinino il modulo e l’argomento del seguente numero complesso:
z=
Si ha:
2 + 2i
√ e i π/2 .
1+ i 3
√
√
|2 + 2 i | ¯¯ i π/2 ¯¯
4+4
2 2 √
|z| = ¯¯
= 2,
=
¯= √
√ ¯¯ ¯ e
2
1+3
¯1 + i 3¯
√ ¢
¡
arg z = arg (2 + 2 i ) − arg 1 + i 3 + π
=
2
√
π π π
= arctan 1 − arctan 3 + π
2 = 4−3+2
5
=
5
12 π .
7
Potenze e radici complesse
La forma esponenziale è la più naturale per esprimere le potenze e le radici dei numeri complessi.
Infatti è sufficiente utilizzare le proprietà dell’esponenziale. Se indichiamo z nella sua forma
esponenziale z = r e i θ si ha:
³
´n
z n = r e i θ = rn e i nθ
Si comprende che se anche si utilizzasse, per rappresentare lo stesso z, un angolo φ che differisce
da θ di un multiplo di 2π, il risultato non cambierebbe:
³
´n ³
´n ³
´n
z n = r e i φ = r e i θ+ i k 2π = r e i θ e i k 2π = rn e i nθ e i n k 2π = rn e i nθ · 1 = rn e i nθ .
Per le radici utilizziamo le stesse proprietà dell’esponenziale, ma trattandosi di potenze frazionarie il rappresentare z con arg z = θ o con un argomento φ che differiscce da θ di un multiplo
di 2π, porta a risultati differenti:
³
´1
³
´1
√
√
1
θ
2π
n
n
n
z = (z) n = r e i θ
= r e i θ+ i k 2π
= n r e i n+i k n .
Si hanno, cioè, n radici distinte, che stanno sulla circonferenza di raggio
che differisce di un multiplo di 2π
n .
8
√
n
r e con un argomento
Seni e coseni complessi
Sia α ∈ R; sommando alla formula di Eulero (3) la sua complessa coniugata, otteniamo
e i α = cos α + i sin α,
e − i α = cos α − i sin α,
e i α + e − i α = 2 cos α,
(4)
mentre sottraendo si ha
e i α − e − i α = 2 i sin α.
(5)
Dalle espressioni (4) e (5) si ricava:
cos α =
e iα + e−iα
,
2
(6)
sin α =
e
iα
−e
2i
−iα
.
I secondi membri delle espressioni (6) hanno significato anche quando α è complesso. Possiamo perciò definire per ogni z ∈ C
cos z =
e iz + e−iz
,
2
(7)
sin z =
e
iz
−e
2i
−iz
.
Si può facilmente dimostrare che, grazie a questa definizione, si possono estendere al campo
complesso molte proprietà delle funzioni trigonometriche reali, quali le formule di addizione, di
6
sottrazione, di duplicazione, le relazioni degli archi associati e cosı̀ via. Inoltre le funzioni sin z
e cos z sono periodiche di periodo 2π; verifichiamo questa affermazione per il coseno:
cos(z + 2kπ) =
=
e i z+2kπ i + e − i z−2kπ i
=
2
e i z e 2kπ i + e − i z e −2kπ i
= cos z.
2
Le funzioni trigonometriche complesse, a differenza di quelle reali, possono avere modulo
maggiore di uno, come è mostrato nel seguente esempio.
Esempio 2 Calcolare cos(2 i ).
cos(2 i ) =
e i (2 i ) + e − i (2 i )
e −2 + e 2
=
= cosh 2.
2
2
Si noti che il risultato è un numero reale più grande di uno. Mediante conti analoghi si
ottiene che
cos( i a) = cosh a,
a ∈ R;
per a → +∞ si ha che
cosh a−→ + ∞;
quindi, per valori grandi di a, si ottengono valori del coseno grandi quanto si vuole.
Nell’esempio precedente si è ottenuto un valore reale del coseno di un numero complesso; in
generale il seno o il coseno di un numero complesso è un numero complesso, il cui modulo può
essere più grande di uno.
9
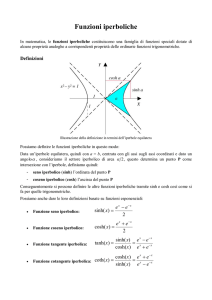
Seni e coseni iperbolici complessi
Richiamiamo la definizione di seno e di coseno iperbolico per un numero t reale:
cosh t =
e t + e −t
,
2
sinh t =
e t − e −t
.
2
(8)
Per t che tende all’infinito i seni e i coseni iperbolici tendono all’infinito in modo esponenziale;
si tratta di funzioni non limitate della variabile reale t. I secondi membri delle espressioni (8)
hanno significato anche per z complesso. Definiamo quindi:
cosh z =
e z + e −z
,
2
sinh z =
e z − e −z
.
2
Osserviamo che in ambito complesso vi è uno stretto legame tra le funzioni circolari e le
funzioni iperboliche:
sin i z
=
cos i z
=
sinh i z
=
cosh i z =
e i ( i z) − e − i ( i z)
2i
e i ( i z) + e − i ( i z)
2
e iz − e−iz
2
e iz + e−iz
2
−z
z
= − i e 2− e
−z
z
= e 2+ e
iz
e−iz
= i e −
2i
= cos z.
7
=
i sinh z,
= cosh z,
=
i sin z,
(9)
che possiamo riassumere nel seguente quadro:
sin i z
=
i sinh z
cos i z
= cosh z
sinh i z
=
(10)
i sin z
cosh i z = cos z
Le funzioni iperboliche complesse sono periodiche di periodo 2π i , vale a dire lungo direzioni
parallele all’asse immaginario. Per k ∈ Z si ha:
sinh z
= sinh(z + 2kπ i )
(11)
cosh z = cosh(z + 2kπ i )
Osserviamo che, mentre ez è sempre diverso da zero, sinh z e cosh z hanno infiniti zeri sull’asse
immaginario . Si ha:
sinh z = 0
=⇒
=⇒
=⇒
=⇒
e z − e −z
e 2z
e 2z
z
= 0
= 1
= e 2kπ i
= kπ i
=⇒
=⇒
=⇒
(12)
cosh z = 0 =⇒
=⇒
=⇒
=⇒
ez
+
e −z
= 0
e 2z = −1
e 2z = e i π+2kπ i
z = i π/2 + kπ i
=⇒
=⇒
=⇒
Con ragionamenti analoghi si può constatare che gli zeri del seno e del coseno (circolari) di
variabile complessa sono gli stessi del seno e del coseno di variabile reale:
sin z = 0
=⇒ z = kπ
cos z = 0 =⇒ z = π/2 + kπ
Osservazione.
Le funzioni di variabile complessa ez , e−z , sin z, cos z, sinh z e cosh z sono combinazioni lineari
le une delle altre; questo spiega perché hanno comportamenti analoghi lungo opportune direzioni
del piano complesso.
10
Logaritmo di un numero complesso
Se r, a ∈ R, il logaritmo (reale) si comporta nel modo seguente:
log (r e a ) = log r + log e a = log r + a log e = (log r) + a.
8
Definiamo il logaritmo complesso (che indichiamo ancora con il simbolo log) in modo che si
conservi questa proprietà; poniamo, per z 6= 0,
³
´
log z = log |z| e i arg z+2kπ i = log|z| + i arg z + 2kπ i ,
con k ∈ Z,
(13)
ove il logaritmo nell’ultimo membro è il logaritmo reale del numero reale positivo |z|.
Si osservi che esiste una analogia tra le radici complesse e i logaritmi complessi, nel senso che
entrambi non forniscono un unico valore. La radice n-esima di un numero complesso fornisce n
valori distinti, mentre il logaritmo complesso ne fornisce infiniti distinti.
Esempio 3 Calcolare il logaritmo complesso di
√
z = 1 − i 3.
Si ha:
³
³ π´
´
log z = log 2 e i (−π/3+2kπ) = log 2 + −
i + 2kπ i .
3
Si osservi che si sono ottenuti infiniti valori, tutti con parte reale uguale a log 2; i punti
corrispondenti stanno su una parallela all’asse immaginario.
Esempio 4 Calcoliamo il logaritmo complesso di i e di −1.
Si ha:
³
´
π
π
= log e i (π/2+2kπ) = log 1 + i + 2kπ i = i + 2kπ i ,
2
2
³
´
i π+2kπ i
log(−1) = log e
= log 1 + π i + 2kπ i = π i + 2kπ i .
log i
Si sono ottenuti, in entrambi i casi, infiniti valori che stanno sull’asse immaginario; nessuno
di essi è reale.
11
Esponenziali con base complessa
Utilizzando i logaritmi complessi si può definire l’esponenziale con base complessa. Se z, w ∈ C
si pone:
z w = e w log z = e w(log |z |+ i arg z+2kπ i )
con k ∈ Z.
Un esponenziale con base complessa ha quindi infiniti valori.
Esempio 5 Calcolare i i .
Dalla definizione che abbiamo introdotto si ha:
i i = e i log i = e i (π i /2+2kπ i ) = e −π/2−2kπ ;
possiamo osservare il fatto che, in questo esempio particolare, si sono ottenuti infiniti valori reali.
9
12
Proprietà delle funzioni circolari e iperboliche
Premettiamo un breve commento di nomenclatura. Le funzioni sin e cos sono dette funzioni
seno e coseno circolari perchè la formula fondamentale che le caratterizza è:
cos2 θ + sin2 θ = 1
(14)
e questa formula permette di dare una rappresentazione parametrica, con parametro θ ∈ [0, 2π),
della circonferenza di raggio r:
µ
¶
½
r cos θ
x = r cos θ
~γ (θ) =
⇐⇒
⇐⇒ x2 + y 2 = r2 .
r sin θ
y = r sin θ
Le funzioni sinh e cosh sono dette funzioni seno e coseno iperbolico perchè la formula fondamentale che le caratterizza è:
cosh2 t − sinh2 t = 1
(15)
e questa formula permette di dare una rappresentazione parametrica, con parametro t ∈ R,
dell’iperbole equilatera di semiasse r e con asintoti le rette y = ±x:
µ
¶
½
r cosh t
x = r cosh t
~γ (t) =
⇐⇒
⇐⇒ x2 − y 2 = r2 .
r sinh t
y = r sinh t
La formula (15) si dimostra facilmente come proprietà dell’esponenziale reale:
µ
¶
¶
µ
t
−t 2
t
−t 2
2
2
e
+
e
e
−
e
cosh t − sinh t =
−
=
2
2
=
e 2t + 2 + e −2t − e 2t + 2 − e −2t =
4
=
2 + 2 = 1,
4
mentre la formula (14) è conseguenza delle proprietà dell’esponenziale complesso:
µ
¶
¶
µ
iθ
−iθ 2
iθ
−iθ 2
e
+
e
e
−
e
2
2
cos θ + sin θ =
+
=
2
2i
=
e 2 i θ + 2 + e −2 i θ − e 2 i θ + 2 − e −2 i θ =
4
=
2 + 2 = 1.
4
Possiamo inoltre asserire che tutte le formule della trigonometria altro non sono che proprietà
dell’esponenziale complesso e quindi devono valere, per le relazioni (9), delle analoghe formule
per le funzioni iperboliche.
Formule di somma e sottrazione
Per le funzioni circolari si ha:
e i α · e i β = (cos α · cos β − sin α · sin β) + i
|
{z
}
k
k
e i (α+β) =
cos(α + β)
+i
10
(cos α · sin β + sin α · cos β) =
|
{z
}
k
sin(α + β)
mentre per quelle iperboliche:
e i i α · e i i β = (cos i α · cos i β − sin i α · sin i β) + i
= (cosh α · cosh β + sinh α · sinh β) −
|
{z
}
k
k
e i i (α+β)
=
cosh(α + β)
−
(cos i α · sin i β + sin i α · cos i β) =
(cosh α · sinh β + sinh α · cosh β) =
|
{z
}
k
sinh(α + β)
Abbiamo cosı̀ ottenuto le formule di somma e sottrazione:
cos(α ± β) = cos α · cos β ∓ sin α · sin β
(16)
sin(α ± β)
= sin α · cos β
± cos α · sin β
cosh(α ± β) = cosh α · cosh β ± sinh α · sinh β
(17)
sinh(α ± β)
= sinh α · cosh β
± cosh α · sinh β
Possiamo dunque riscrivere tutte le formule di trigonometria ricordando semplicemente che
cos i α = cosh α e sin i α = i sinh α.
Formule di duplicazione
Ponendo β = α nelle formule di somma e sottrazione si ottengono le formule di duplicazione:
cos 2α = cos2 α − sin2 α = 1 − 2 sin2 α = 2 cos2 α − 1
(18)
sin 2α
= 2 · sin α · cos α
cosh 2α = cosh2 α + sinh2 α = 1 + 2 sinh2 α = 2 cosh2 α − 1
(19)
sinh 2α
= 2 · sinh α · cosh α
Formule del cos2 e del sin2
Dalla formula di duplicazione del coseno si ricavano facilmente le seguenti formule:
cos2 α =
2
sin α
=
cosh2 α =
2
sinh α
=
1
2 (1
+ cos 2α)
1
2 (1
− cos 2α)
(20)
1
2 (cosh 2α
+ 1)
1
2 (cosh 2α
− 1)
Formule di bisezione
11
(21)
Dalle formule del cos2 e del sin2 , ponendo α/2 al posto di α e estraendo la radice quadrata, si
hanno le formule di bisezione:
cos
α
2
q
= ± 12 (1 + cos α)
sin
α
2
q
= ± 12 (1 − cos α)
cosh α2
sinh
α
2
q
=
1
2 (1
(22)
+ cosh α)
q
= ± 12 (cosh α − 1)
(23)
Formule di Werner
Sommando e sottraendo opportunamente le formule di somma e sottrazione si ottengono le
seguenti espressioni:
cos α cos β =
1
2 (cos(α
− β) + cos(α + β))
sin α sin β
=
1
2 (cos(α
− β) − cos(α + β))
sin α cos β
=
1
2 (sin(α
+ β) + sin(α − β))
cosh α cosh β =
1
2 (cosh(α
+ β) + cosh(α − β))
sinh α sinh β
=
1
2 (cosh(α
+ β) − cosh(α − β))
sinh α cosh β
=
1
2 (sinh(α
+ β) + sinh(α − β))
(24)
(25)
Formule di prostaferesi
Se si scrivono le formule di Werner con x al posto di α e y al posto di β e poi si opera la
sostituzione:
½
x+y =α
x−y =β
e quindi

 x=

y=
12
α+β
2
α−β
2
si ottengono facilmente le seguenti formule di prostaferesi:
α−β
cos α + cos β = 2 cos α+β
2 cos 2
α−β
cos α − cos β = −2 sin α+β
2 sin 2
α+β
2
cos
(26)
α−β
2
sin α + sin β
= 2 sin
sin α − sin β
α−β
= 2 cos α+β
2 sin 2
α−β
cosh α + cosh β = 2 cosh α+β
2 cosh 2
α−β
cosh α − cosh β = 2 sinh α+β
2 sinh 2
13
α+β
2
cosh
(27)
α−β
2
sinh α + sinh β
= 2 sinh
sinh α − sinh β
α−β
= 2 cosh α+β
2 sinh 2
Bibliografia
H.B. Dwight, Tables of Integrals and Other Mathematical Data, Macmillan, New York (1961).
M.R. Spiegel, Complex Variables, McGraw-Hill Book, New York (1964).
14
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Indice
−
−
−
−
−
−
−
−
−
−
−
−
−
−
Sommario
Forma cartesiana
Forma matriciale
Forma cartesiana con la i
Forma polare trigonometrica
Forma esponenziale
Alcune proprietà del modulo e dell0 argomento
Potenze e radici complesse
Seni e coseni complessi
Seni e coseni iperbolici complessi
Logaritmo di un numero complesso
Esponenziali con base complessa
Proprietà delle funzioni circolari e iperboliche
Bibliografia
Indice
13