Soluzione

Economia Politica 2 - MICROECONOMIA
ESERCITAZIONE 6
Testi esercitazione 21 Novembre 2002
SOLUZIONI
ESERCIZIO 1
Un monopolista fronteggia una curva di domanda di mercato: P = 100 – 4q
I suoi costi di breve periodo sono dati dalla funzione: CT = 20q
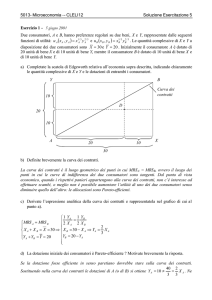
a) Disegnate la funzione di domanda, la curva MR e la curva MC.
P
Profitto di
monopolio
100
60

Perdita
secca di
monopolio
E


MC
20
RM
10
AR = domanda
20
q
25
b) Calcolate l’equilibrio del monopolista: quantità (q*) e prezzo (P*).
MC = MR,
dalla funzione di costo: MC = 20 (costante)
dalla funzione di domanda inversa: MR = 100 – 8q, da cui:
100 –8q = 20  80 = 8q  q* = 10, sostituisco nella funzione di domanda :
P = 100 –4q*  P* = 60
1
c) Calcolate e disegnate l’area del profitto (Π) di monopolio.
Π = R – C  (100q – 4q2) – 20q
Π(q*) = 1000 – 400 – 200 = 400, profitto di monopolio  coincide con il
rettangolo scuro nella figura (Area ).
Può essere alternativamente ricavato come: Π = AVΠ ·q* , profitto medio per la
quantità di equilibrio, dove AVΠ = AR – AC
(60 – 20) ·10  Π = 400.
d) Calcolate e disegnate la perdita secca di monopolio e motivatene l’esistenza.
Per calcolare la perdita secca di monopolio devo preventivamente calcolare quale
sarebbe la quantità prodotta in concorrenza perfetta: AR = MC = P
Qui: 100 –4q = 20  80 = 4q  q* = 20, quantità di equilibrio di concorrenza.
La perdita secca di monopolio è pari all’area del triangolo scuro (area ) e
discende dal fatto che a un prezzo superiore al MC, il prezzo di monopolio,
l’offerta scende: una parte di produzione non viene realizzata e non può essere
appropriata, in termini di surplus, né dal consumatore, né dal produttore.
Perdita = (60 – 20) ·(20 – 10) / 2 = 400/2 = 200
e) In che senso (ed eventualmente per chi) la discriminazione al prezzo del I ordine
(discriminazione perfetta) sarebbe preferibile?
La discriminazione perfetta prevede che ad ogni consumatore venga applicato
esattamente il proprio prezzo di riserva (la cifra massima che il consumatore è
disposto a pagare per consumare una unità di bene). In questo modo la
produzione cresce oltre la quantità di equilibrio di monopolio (q* = 10). Il
monopolista infatti non è costretto ad abbassare il prezzo su tutte le unità
inframarginali. La produzione cresce fino a q* = 20, quantità di equilibrio di
concorrenza perfetta.
I profitti del monopolista sono ora coincidenti col surplus totale dell’economia e
precisamente a Π = 20*80/2 = 800.
Il benessere complessivo della società cresce, perché viene meno la perdita secca
di monopolio precedentemente presente, il surplus del monopolista cresce (nel
caso in esame raddoppia) perché il suo profitto si accresce della precedente area
di perdita secca e del precedente surplus del consumatore. Quest’ultimo è l’unico
a peggiorare la propria posizione in termini di benessere, dal momento che il suo
surplus viene trasferito al monopolista. Ma in termini di efficienza, questa
situazione risulta preferibile rispetto al monopolista non discriminante.
Riassumendo, in equilibrio di monopolio:
surplus del consumatore = area ; surplus del produttore = area ; perdita secca
di benessere = area ; surplus dell’economia = +.
In presenza di discriminazione perfetta:
2
surplus del consumatore  si annulla; surplus del produttore = area ++;
perdita secca di benessere  si annulla; surplus dell’economia = ++.
Supponete ora che venga imposta una tassa sul monopolista, di aliquota t proporzionale alla
quantità prodotta, e che l’aliquota sia pari a: t = 8.
f) Calcolate il nuovo equilibrio del monopolista: quantità (q*) e prezzo (P*); calcolate
inoltre il profitto di monopolio (Π) e l’entrata fiscale (T) per l’amministrazione
finanziaria.
Π = R – C –tq
Π = 100q – 4q2 – 20q –8q = 72q –4q2, la massimizzazione impone che:
Π’ = 0  72 –8q = 0  q* = 9, produzione di equilibrio del monopolista dopo
l’introduzione della tassazione
P = 100 –4q* = 100 – 36  P* = 64
Π = (100q – 4q2) – 20q - 8q per q* = 9 dà Π = 324 (profitto del monopolista)
L’entrata tributaria complessiva è pari a T = t ·q* = 8 ·9 = 72
Il surplus del consumatore = 9*36/2=162
(si può notare come il surplus totale dell’economia si riduca a 324+72+162=558,
con una diminuzione dell’efficienza complessiva di 42 unità rispetto alla
situazione ante-imposta, che vedeva un surplus totale di 400+200=600).
ESERCIZIO 2
(Prova di Esame di Microeconomia del 3 Settembre 2001)
Un monopolista fronteggia la seguente curva di domanda P = a - bQ.
a)
Sapendo che i costi totali di produzione sono del tipo TC = cQ, si calcoli l’equilibrio
(prezzo, quantità e profitti).
b)
Si calcoli analiticamente e si mostri graficamente la perdita secca.
Soluzione:
a)
Il monopolista massimizza i profitti  = P*Q – TC, cioè in questo caso:
max  = (a – bQ)*Q – cQ,
la cui condizione di primo ordine d / dQ = a – bQ – bQ – c = 0.
Riscritta tale condizione equivale all’utilizzo della regola MR=MC, ovvero a-2bQ=c
3
(MR per funzione di domanda lineare è equivalente ad una retta con stessa intercetta
verticale della funzione di domanda e doppio coefficiente angolare).
Risolvendo per Q la precedente espressione troviamo la quantità di equilibrio per il
monopolista: QM = (a-c) / 2b.
Se sostituiamo la quantità d’equilibrio nella funzione di domanda otteniamo il prezzo di
equilibrio P M = a-b*(a-c) / 2b che, semplificata, fornisce P M =(a+c)/2.
Infine, i profitti del monopolista  = QM* P M – c* QM; sostituendo nell’espressione prezzo e
quantità d’equilibrio, otteniamo: [(a-c) / 2b]*[ (a+c)/2] – c*[(a-c) / 2b]. Dopo semplici
calcoli e semplificazioni, arriviamo a  = (a-c)2 / 4b.
b)
Dapprima illustriamo graficamente la situazione di monopolio con i valori trovati ed
evidenziamo sul grafico l’area corrispondente alla perdita secca:
P
PM
EM
MR
D
c
ECP
A
-2b
QM
-b
QCP
Q
Il triangolo EMAECP rappresenta graficamente la perdita secca.
Per calcolarne analiticamente l’ammontare, dobbiamo determinare il valore di QCP, intersecando
la curva di domanda con la curva (orizzontale) di costo marginale e risolvendo per la quantità.
Otteniamo a-bQ = c, da cui QCP=(a-c)/b.
L’area del triangolo EMAECP = {[(a-c)/b – (a-c)/2b] * [(a+c)/2 – c]} risulta, dopo pochi passaggi,
uguale a (a-c)2 / 8b.
4
ESERCIZIO 3
L’impresa Alfa, monopolista sul mercato, fronteggia la seguente curva di domanda: p = 360 – 4y,
dove p è il prezzo e y è la quantità prodotta. I costi dell’impresa sono dati dalla funzione: C = 2y2
a) Ottenete le funzioni dei ricavi marginali, dei costi medi e dei costi marginali del monopolista
MR = 360-8y
MC=4y
AC = 2y
b) Calcolate la quantità di equilibrio e il prezzo praticato dal monopolista.
MR=MC  360-8y = 4y  y* = 30
p* = 360- 120=240
c) Nel punto di equilibrio, l’elasticità è maggiore, minore o uguale a 1? Motivate la risposta senza
svolgere calcoli.
MR = p (1-1/). In equilibrio, MR=MC MR>0   >1
a) Calcolate il profitto di equilibrio del monopolista e rappresentate l’area del profitto sul grafico.
 = py - 2y2 = 240*30 - 2*302 = 7200-1800 = 5400 (area in grassetto)
In alternativa, differenza MR e MC, rappresentata dall’ area del triangolo ABO.
MC
AC
P
A
360
E
240

B
MR
D
O
y
30
5
b) Calcolate il surplus del consumatore e il surplus totale dell’economia nel punto di equilibrio.
Surplus consumatore = area compresa fra la curva di domanda e il prezzo di mercato =
[(360-240) 30] / 2 = 1800
Surplus complessivo = surplus produttore + surplus consumatore = 5400+1800 = 7200
f) Supponete ora che il monopolista possa attuare una discriminazione di prezzo del primo ordine.
Definite il concetto di discriminazione di prezzo del primo ordine. Quale sarebbe la quantità di
equilibrio in questo caso?
La discriminazione di prezzo di primo ordine è una pratica che consente all’impresa di vendere
ciascuna unità esattamente al prezzo a cui i consumatori sono disposti a pagarla.
P= MC  360-4y=4y y*=45
g) A seguito della discriminazione di prezzo il surplus del consumatore e il surplus totale
dell’economia aumentano, diminuiscono o rimangono costanti rispetto alla situazione descritta al
punto e)? Motivate le risposte senza svolgere calcoli.
Se il monopolista discrimina perferttamente, il surplus del consumatore è nullo (il consumatore
acquista ogni unità esattamente al prezzo a cui è disposto a pagarla). Il surplus dell’economia
aumenta con la discriminazione (raggiunge il massimo valore) e coincide con il surplus del
produttore.
6
ESERCIZIO 4
Una nota casa farmaceutica tedesca elabora un vaccino anti-influenzale, la cui assunzione determina
una copertura contro tutte le possibili variabili di questa malattia nell’arco dei dieci anni successivi
alla vaccinazione. Per tutta la durata del brevetto l’impresa farmaceutica può considerarsi
monopolista rispetto alla domanda di questo bene, dato che i comuni vaccini non garantiscono una
copertura superiore all’anno. L’impresa produce il farmaco in un unico impianto, che ha costi totali
di produzione pari a C(Y) = 100 + 8Y, mentre può scegliere di vendere il prodotto nel mercato
nazionale (in quantità yN ed applicando un prezzo PN) o all’estero (in quantità yE e prezzo PE), con
Y= yN+ yE.
Date le funzioni di domanda indiretta nel mercato nazionale yN(PN) = 400/(PN)2 e nel
a)
mercato estero yE(PE) = 1000/(PE)3, ricavate prezzi e quantità di equilibrio in entrambi i
mercati.
La condizione richiesta è simile a quella utilizzata per l’allocazione ottima della produzione. Se,
in quel caso, dovevamo uguagliare costi marginali differenti ad un’unica espressione del ricavo
marginale, adesso abbiamo un solo impianto che produce per due differenti mercati; cioè,
abbiamo uno stesso costo marginale da uguagliare ai ricavi marginali ottenuti da due diverse
funzioni di domanda.
Per prima cosa, quindi, dobbiamo calcolare le due funzioni inverse di domanda, da cui ricavare
le espressioni dei ricavi marginali.
Per il mercato nazionale abbiamo: (PN)2= 400 / yN, da cui PN = 20 / (yN)1/2
Calcoliamo i ricavi totali sul mercato nazionale TR N = PN * yN, = 20 / (yN)1/2 * yN, = 20(yN)1/2 e,
da qui, calcoliamo i ricavi marginali sul mercato nazionale MR N = d TR N / dyN, = 20*1/2 (yN) 1/2
= 10 / (yN) ½ .
Procediamo in maniera analoga per il mercato estero: (PE)3 =1000/yE, da cui PE=10 / (yN)1/3
Calcoliamo i ricavi totali sul mercato estero TR E = PE * yE, = 10 / (yE)1/3 * yE, = 10 (yE)2/3 e
calcoliamo i ricavi marginali sul mercato estero MR E = dTR E / dyE, = 10*2/3*(yE) -1/3
= 20 /[3 (yE)1/3 ].
I costi marginali risultano MC = dC(Y)/dY = 8.
Da MR N =MC abbiamo 10 / (yN) ½ = 8 da cui (yN) ½ =10/8 che, semplifiando ed elevando
entrambi i membri al quadrato, fornisce yN, = (5/4)2, cioè la quantità prodotta nel mercato
7
nazionale. Il prezzo praticato in questo mercato è ricavato sostituendo il valore numerico di
yN, nella funzione di domanda interna: PN = 20 / [(5/4)2] 1/2 = 20*4/5 = 16.
Da MR E =MC abbiamo 20 /[3 (yE)1/3 ] = 8 da cui (yE)
1/3
=20/3*8 che, semplificando ed
elevando entrambi i membri al cubo, fornisce yE, = (5/6)3
Come in precedenza, per trovare il prezzo applicato sui mercati esteri, bisogna sostituire il
valore numerico di yE nella relativa funzione di domanda: PE =10 / [(5/6) 3] 1/3 = 10*6/5 =
12.
b)
Verificate che il monopolista applica un prezzo più elevato nel mercato a domanda più
rigida.
Il secondo punto richiede di verificare la seguente relazione PN > PE  N < E.
Dobbiamo quindi calcolare i valori delle elasticità sul mercato nazionale ed estero,
utilizzando la consueta formula per il calcolo dell’elasticità (calcolo la derivata rispetto al
prezzo nella funzione di domanda ricavata al punto a e sostituisco i valori numerici di prezzi
e quantità relativi ai singoli mercati, anch’essi ottenuti come soluzione al primo punto).
N =
dy N PN
= 0,1953125*10,24 = 2.
dPN y N
E =
dy E PE
= 0,1447*20,736= 3.
dPE y E
Effettivamente il monopolista applica un prezzo più elevato nel mercato a domanda più
rigida.
8