ISOTOPI
Molti elementi nella tavola periodica non hanno massa atomica intera (es. Cl ha massa atomica =
35.45), questo è dovuto al fatto che vi sono nuclei con stesso numero di protoni (Z) ma diverso
numero di neutroni (N).
Quindi in natura possono esistere elementi stabili composti da uno stesso numero di protoni (Z)
ma un numero diverso di neutroni (N).
In geochimica gli ISOTOPI sono i
nuclidi più utilizzati.
Gli isotopi di un elemento
possono essere radioattivi o
stabili.
La massima parte degli elementi
in natura è costituita da miscele
di isotopi stabili.
Ne consegue che a parità di numero atomico, o protoni (Z), tali elementi differiscono per numero
di massa (A=N+Z): questi nuclidi di uno stesso elemento sono detti ISOTOPI (dal greco iso-topos
= eguale posto, nella tavola periodica, dato che si tratta di atomi con lo stesso nome), con eguale
Z ed A diverso (per esempio 11H, 21H; 31H oppure 126C, 136C, 146C).
Esistono in natura anche degli elementi diversi con uguale massa atomica o stesso numero di
neutroni:
ISOBARI (dal greco iso-baros = con lo stesso peso), con Z diverso, (perciò chimicamente
diversi) ed A uguale (4018Ar, 4019K, 4020Ca)
ISOTONI (con lo stesso numero di neutroni), cioè con A - Z uguale (per esempio 21H [2-1=1],
3 He [3-2=1]
2
ISOTOPI
Generalmente si usa rappresentare un determinato isotopo con il nome o il simbolo dell’
elemento di appartenenza e col numero di massa.
Per esempio per rappresentare i tre isotopi naturali dell’ossigeno si ricorre ai simboli:
A
Z
16
17 O
O,
8
8
e
18
8O
dove in alto è riportato il numero di massa A, ed in basso è indicato il numero atomico Z
(numero di protoni). Oppure:
16O, 17O
e 18O
dove in alto è indicato il numero di massa A ed il numero atomico Z è considerato implicitamente
uguale e noto.
In natura sono stati riconosciuti 290 differenti isotopi variamente distribuiti tra tutti gli elementi:
mentre pochi elementi sono presenti in natura con un solo isotopo, come il fluoro (F) e l’oro (Au),
la maggioranza sono presenti con vari isotopi, fino a dieci nel caso dello stagno (Sb).
Oltre agli isotopi naturali, vi sono isotopi artificiali prodotti attraverso opportune reazioni nucleari.
Altri elementi infine, quali i transuranici (Z>92), non individuati in natura in quantità apprezzabili,
sono noti soltanto attraverso i loro isotopi artificiali radioattivi.
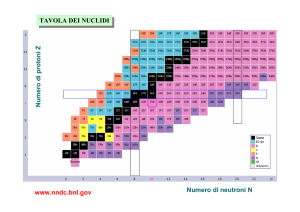
NUMERO DI MASSA (A=N+Z)
CURVA DI STABILITÀ DEI NUCLEI ATOMICI.
promezio Pm
Z=83 (Bi) Per nuclidi atomici leggeri la configurazione
nucleare risulta stabile quando N/Z = 1, cioè
il numero dei protoni = numero dei neutroni
(linea verde in figura).
Al crescere del numero dei protoni (Z) il
numero di neutroni (N) necessari a garantire
la stabilità del nuclide aumenta.
Nella figura sono riportati, in funzione di Z e
di A (=N+Z), tutti i nuclidi stabili cioè tutti
quelli riscontrati in natura.
Mancano perciò quelli artificiali e quelli
radioattivi; in particolare si può notare la
mancanza del nuclide con Z=43 (tecnezio Tc)
e con Z=61 (promezio Pm), che sono
artificiali, benché abbiano Z relativamente
basso (ma ambedue dispari).
tecnezio Tc
Il grafico si ferma a Z=83 (bismuto Bi),
poiché tutti i nuclidi con Z>83 sono instabili
e radioattivi, e molti di essi artificiali (Z>96).
NUMERO DI PROTONI (Z)
Z>83
ISOTOPI STABILI
Numero di PROTONI (Z)
Gli isotopi stabili sono quelli con massa atomica piccola, quindi gli isotopi di uno stesso elemento
avranno una differenza di massa atomica relativamente grande. Tra i più studiati vi sono
l’ossigeno, il carbonio, l’idrogeno, lo zolfo, l’azoto.
A
In figura sono riportati gli
isotopi di alcuni elementi
ordinati per numero di
neutroni e numero di
protoni.
Quelli
con
il
riquadro riempito di nero
sono quantitativamente più
abbondanti in natura.
Numero di NEUTRONI (N)
RADIOATTIVITÀ
La radioattività è una conseguenza dell’ instabilità di alcuni nuclei (con N/Z > 1 e Z ≥ 83). Un
nuclide instabile tende, emettendo radiazioni, a raggiungere la fascia di stabilità dei nuclei: in
pratica si passa da nuclidi ad alta massa atomica (A) e numero atomico (Z) a nuclidi di più bassa
massa e numero atomico.
Il decadimento radioattivo può avvenire attraverso vari tipi di processi, che sono sinteticamente
riassunti in tabella:
processo
particelle
coinvolte
variazione di numero
atomico Z (protoni)
variazione di massa atomica
A (protoni+ neutroni)
emissione α
nuclei di He
-2
-4
emissione β-
elettroni
+1
-
emissione β+
positroni
-1
-
emissione γ
radiazioni
-
-
cattura elettronica
elettroni
-1
-
I tipi di processi coinvolti nel decadimento radioattivo sono: i primi tre con emissione di particelle, il
quarto di radiazioni; il quinto non è un vero processo di decadimento, ma ne ha gli stessi effetti: è
dovuto alla cattura di un elettrone da parte del nucleo.
Gli isotopi radiogenici sono quegli elementi che si formano per decadimento
radioattivo (radioattività) naturale.
DECADIMENTI RADIOATTIVI
neutrone
protone
β-
v-
Emissione β-: vengono emessi una particella
carica negativa dal nucleo ed un antineutrino
(v-). La particella carica negativa, detta β- o
negatrone o elettrone nucleare, non è un
elettrone degli orbitali. Nel nucleo un
neutrone si trasforma in protone con aumento
di una unità per Z, mentre A resta costante. I
nuclidi che subiscono questo tipo di
decadimento sono tra gli altri:
3
1H
14
40
protone
neutrone
β+
v
6C
19K
3
2He
+ 0-1β- + v-
7N
+ 0-1β- + v-
14
40
20Ca
+ 0-1β- + v-
Emissione β+: vengono emessi positroni,
particelle con la stessa massa dell'elettrone
ma carica positiva (β+ ) e un neutrino (v); si ha
diminuzione di una unità per Z, aumenta N e
quindi A resta costante. Un esempio di nuclidi
che sono soggetti a decadimento β+ sono:
11
6C
11
5B
+ 01β+ + v
18
9F
18
8O
+ 01β+ + v
DECADIMENTI RADIOATTIVI
Emissione α: questo tipo di decadimento è
caratteristico dei nuclei più pesanti e vengono
emesse particelle α (nuclei 42He) ed energia
(Q), perciò si ha una diminuzione di 2 unità per
Z e di 4 per A. Quale esempio riportiamo:
210
84Po
206
82Pb
+ 42He + Q
232
90Th
228
88Ra
+ 42He + Q
235
92Pb
231
90Th
+ 42He + Q
238
92Po
234
90Th
+ 42He + Q
Emissione γ: vengono emesse non particelle
ma radiazioni altamente energetiche (più dei
raggi X). Tale decadimento è caratteristico dei
nuclei in uno stato eccitato ad esempio:
234
90Th*
234
90Th
+γ
In questa emissione non c'è alcuna variazione di
A né di Z;
Cattura elettronica: non è una emissione, ma ne ha gli stessi effetti: un elettrone viene catturato dal
nucleo e si lega con un protone; un protone si trasforma in neutrone perciò Z diminuisce di una unità ed
A resta costante. La cattura elettronica corrisponde alla reazione:
195
79Au
+ 01e
195
78Pt
FAMIGLIE RADIOATTIVE
Il nuclide prodotto durante un decadimento radioattivo può essere egli stesso radioattivo e
continuare a decadere fino ad una configurazione stabile. In tal caso il radionuclide di partenza
viene chiamato capostipite e i prodotti intermedi e finali sono raggruppati come famiglia
radioattiva. Le famiglie radioattive sono tre ed hanno come capostipite:
238U
(serie uranio
235U
(serie uranio-attinio) che termina con 207Pb,
232Th
radio) che termina con 206Pb,
(serie torio D) che termina con il 208Pb.
emissione α
232
90Th
208
82Pb
+ 642He + 4β
β-
235
92U
207
82Pb
+ 742He + 4β
β-
238
92U
206
82Pb
+ 842He + 6β
β-
Il piombo si presenta come una
miscela di quattro isotopi stabili:
204Pb (abbondanza: 1,4%), 206Pb
(24,1%), 207Pb (22,1%) e 208Pb
(52,4%).
Figura schema di decadimento 232Th (da Longinelli e Deganello).
GEOCHIMICA ISOTOPICA DELLE ROCCE E MINERALI
La geochimica degli isotopi radiogenici ha due utilizzazioni principali:
•
•
datazione delle rocce e minerali – GEOCRONOLOGIA
identificazione di processi geologici e sorgenti – GEOCHIMICA ISOTOPICA
L’utilizzo degli isotopi radiogenici si basa su due assiomi:
Il decadimento radioattivo è un processo indipendente dall’influenza di fattori
esterni quali temperatura e pressione (etc.);
Due isotopi di uno stesso elemento hanno comportamento chimico uguale, quindi
processi chimici non possono cambiare o frazionare il rapporto tra due isotopi dello
stesso elemento. I processi che consideriamo in geologia sono quelli che
intervengono tra minerale, fuso, vapore o soluzioni acquose.
Nei sistemi chimici pertinenti alla geologia, il comportamento chimico degli elementi è determinato
dal numero atomico Z (Potenziale Ionico).
Per cui isotopi di uno stesso elemento pur avendo masse diverse, hanno comportamento chimico
uguale.
In realtà i due assiomi non sono veri in assoluto, ma le influenze nei rapporti isotopici di uno
stesso elemento nei sistemi geologici sono trascurabili o misurabili.
Sistemi isotopici principali utilizzati per lo studio dei processi geologici e
sorgenti magmatiche: rapporti isotopici.
decadimento
87Rb
87Sr
rapporto isotopico
87Sr/86Sr
147Sm
143Nd
143Nd/144Nd
232Th
208Pb
208Pb/204Pb
235U
207Pb
238U
206Pb
207Pb/204Pb
206Pb/204Pb
176Lu
176Hf
176Hf /177Hf
187Re
187Os
187Os /186Os
radiogenico
Sr
Sr
stabile
I rapporti isotopici in un magma sono ereditati dalla roccia sorgente da cui il
magma è stato estratto. Tale rapporto rimane inalterato durante i successivi
processi di frazionamento che portano alla differenziazione del magma.
Questo perché la differenza di massa tra due isotopi dello stesso elemento è così piccola che i
processi (magmatici) controllati dagli equilibri cristallo-liquido non possono modificarli. Inoltre
due isotopi dello stesso elemento presentano stesso numero di protoni (Z) quindi stesso
numero di elettroni subiscono gli stessi processi chimici di ionizzazione (acquisto o perdita di
elettroni).
L’isotopo genitore ha compatibilità diversa rispetto all’isotopo figlio (radiogenico)
10000
#63
#64
#70
1000
sample/PM
100
10
1
0.1
0.01
RbBaTh U PbNbTa La Ce Pr Sr P Nd Zr HfSmEu Ti GdTbDy Y Ho ErTmYbLu Zn V Co Cr
Questo determina un arricchimento diverso e un diverso rapporto tra padre/figlio.
Queste differenze sono utili per ricostruire le evoluzioni dei magmi ma anche i
serbatoi da cui i magmi si formano.
Es. Rb è più abbondante nella crosta, quindi il
rapporto nelle rocce mantelliche.
87Sr/86Sr
nelle rocce crostali è > dello stesso
I rapporti isotopici in
un
magma
sono
ereditati dalla roccia
sorgente
Ogni
sorgente
magmatica ha la sua
impronta
isotopica
caratteristica
Mixing tra due sorgenti
magmatiche distinte può
essere riconosciuto (e
modellizzato)
Da Rollinson H.: Using
Geochemical data
RESERVOIR MANTELLICI
Zindler and Hart (1986) hanno individuato 5 composizioni isotopiche limite (end-members) nel
mantello da cui per mixing era possibile spiegare le composizioni isotopiche di tutti i magmi eruttati
lungo le dorsali oceaniche (MORB) e dalle Isole Oceaniche (OIB).
Diagrammi di Correlazione Isotopici
Esempio: confronto rapporti isotipici
Sr-Nd in zone di subduzione.
Gli isotopi vengono utilizzati per definire le sorgenti magmatiche ed i processi di
differenziazione magmatica, ma anche per studiare l’evoluzione del mantello, della crosta
terrestre e le sue componenti, sia i minerali che le rocce.
87Sr/86Sr 143Nd/144Nd 206Pb/204Pb 207Pb/204Pb 208Pb/204Pb
DMM
EM-1
EM-2
HIMU
FOZO1
0.70100
0.70530
0.70780
0.70285
0.70244
0.51300
0.51236
0.51258
0.51285
0.51314
17.200
17.650
19.000
22.000
19.340
15.400
15.470
15.680
15.850
15.560
Bell K., Castorina F., Rosatelli G., and Stoppa F. (2006). PLUME
ACTIVITY, MAGMATISM, AND THE GEODYNAMIC EVOLUTION
OF THE MEDITERRANEAN. Annales Geophysicae, 48, 891-905.
37.400
38.100
39.500
40.700
39.000
Isotopic composition of
MORB and OIBs endmembers.
GEOCHIMICA ISOTOPICA APPLICATA ALLA DATAZIONE DI ROCCE E MANUFATTI
Gli isotopi hanno una grande importanza nello studio sia dei processi naturali che dei materiali
organici ed inorganici.
Un impiego della geochimica isotopica è la datazione assoluta di materia organica ed
inorganica.
Inoltre gli isotopi possono essere utilizzati per tracciare le sorgenti dei minerali, manufatti e
materiali lapidei distribuiti nello spazio e nel tempo, anche durante la preistoria. Nelle opere di
restauro lo studio isotopico dei materiali lapidei è fondamentale per determinare le aree di
provenienza o di cava dei materiali stessi.
Luoghi di estrazione e commercializzazione
dell’ossidiana nel Neolitico. Per tali studi sono
stati utilizzati anche gli isotopi del Sr e Nd.
Gli isotopi sono utili anche per lo studio dell’atmosfera e dell’idrosfera, sia per determinare le
caratteristiche naturali sia per individuare inquinamenti e sorgenti inquinanti Es. δ18O vs δ15N.
Consideriamo 18O/16O vs 15N/14N
Figura 1 - individuazione delle diverse fonti dei nitrati in soluzione sulla base della loro composizione isotopica
(modificato da Clark e Fritz, 1997); Da http://www.iso4.it/nitrati.htm.
GEOCRONOLOGIA
La scoperta della radioattività ha determinato lo sviluppo di un
metodo attendibile per la determinazione dell’età assoluta di rocce e
minerali contenenti isotopi radioattivi: la datazione radiometrica.
L’attendibilità di tale metodo è dovuta al fatto che la velocità di
decadimento di un isotopo radioattivo è costante e indipendente da
qualsiasi fattore fisico o chimico.
Le datazioni si basano sulla determinazione dei rapporti di
concentrazione tra nuclide radioattivo progenitore e il nuclide
stabile prodotto da decadimento radioattivo, detto elemento figlio.
L’ETÀ
RADIOMETRICA
INDICA
L’INTERVALLO
DI
TEMPO
TRASCORSO DAL MOMENTO IN CUI IL SISTEMA CONSIDERATO, È
DIVENTATO UN SISTEMA CHIUSO PER UNO O PIÙ ELEMENTI PRESI
IN ESAME, FINO AL MOMENTO DELLA MISURA.
LA LEGGE DEL DECADIMENTO RADIOATTIVO
Qualsiasi decadimento radioattivo segue una legge che prevede una diminuzione esponenziale
nel tempo del numero di nuclei non ancora decaduti N(t), secondo la relazione:
[1]
Nt = N0 e-λλt
dove N0 è il numero di nuclei iniziali (t = 0 o tempo di chiusura del sistema)
λ è è la COSTANTE DI DECADIMENTO caratteristica di ogni
(indipendentemente dalla temperatura e dai legami chimici).
elemento
La costante di decadimento rappresenta la probabilità di decadimento di un nucleo
nell'unità di tempo; il suo inverso, τ, viene detto VITA MEDIA del nucleo.
Il tempo occorrente perché metà dei radionuclidi decada, cioè si abbia:
Nt = N0/2
è detto TEMPO DI DIMEZZAMENTO o periodo di semitrasformazione.
Esplicitando la funzione [1] per t, si ottiene:
t = - (1/λ
λ) ln (Nt/N0)
TEMPO DI DIMEZZAMENTO
Il tempo di dimezzamento ha un valore caratteristico per ogni isotopo radioattivo e ne esprime la
velocità di disintegrazione. Ad esempio, se partiamo da un grammo di isotopo radioattivo, dopo
che sarà trascorso un tempo pari al suo tempo di dimezzamento resterà di quell’isotopo solo
mezzo grammo; di questo mezzo grammo la metà (ossia un quarto di grammo) sarà decaduta
dopo che sarà trascorso un altro tempo pari al tempo di dimezzamento, e così via.
La velocità di decadimento è il numero di disintegrazioni spontanee che avvengono in un secondo
e viene chiamata ATTIVITÀ.
In tabella 1, sono riportati i principali sistemi isotopici utilizzati in geocronologia.
Tabella 1. Sistemi di decadimento radioattivo con tempi di dimezzamento lunghi
.
[Da W.M. White (Table 8.2, pag. 328)]
METODI GEOCRONOLOGICI
I metodi geocronologici più utilizzati in geologia e archeologia sono quelli basati su:
1. Scomparsa di un isotopo radioattivo genitore (es. 14C)
2. Accumulo di un isotopo radiogenico figlio (es. 40K/40Ar)
Determinando con opportune analisi la percentuale di un isotopo radioattivo (progenitore) ancora
presente e quella di isotopo stabile (figlio) già prodotto, si può risalire all’età del campione in
esame.
Tabella. Isotopi utilizzati per le datazioni di materiale organico ed inorganico
Elemento
progenitore
Tempo di dimezzamento
(in anni)
Elemento figlio
Materiali databili
14C
(Carbonio-14)
5730 ± 40
14N
(Azoto-14)
Materiali organici
40K
(Potassio-40)
1,25 miliardi (10x109)
40Ar
(Argon-40)
Muscovite, Biotite, Orneblenda,
K-Feldspato - Rocce ignee
(Stronzio-87)
Miche, K-Feldspato
metamorfiche
207Pb
(Piombo-207)
Zircone, Uraninite, Pechblenda
4,47 miliardi
206Pb
(Piombo-206)
Zircone, Uraninite, Pechblenda
13,9 miliardi
208Pb
(Piombo-208)
Rocce vulcaniche
87Rb
(Rubidio-87)
48,8 miliardi (10x109)
87Sr
235U
(Uranio-235)
707 milioni
238U
(Uranio-238)
232Th
(Torio-232)
-
Rocce
METODO DEL CARBONIO 14 (radiocarbonio)
Questo metodo si applica alla datazione di sostanza organica. Il metodo fu sviluppato da W.F.
Libby nel 1940 si basa sul principio che sia gli organismi animali che vegetali assorbono con il
metabolismo 146C che non viene reintegrato dopo la morte. Tale metodo è il più utilizzato in
Archeologia.
Con tale metodo si possono datare pitture rupestri, insediamenti umani, resti umani e animali,
tessuti...
METODO DEL CARBONIO 14 (radiocarbonio)
Il carbonio ha tre isotopi, due stabili: 126C e 136C, ed uno radiogenico, il 146C.
Il 146C si forma nell’alta atmosfera per reazione nucleare tra radiazione cosmica secondaria e
nuclidi di azoto presenti nell’atmosfera dalla reazione:
1
14
14
7N
+
1
0n
14
6C
+
7N
Reazioni di Spallazione.
La radiazione cosmica primaria e
secondaria fornisce neutroni che
impattando con il nucleo di un atomo
producono, nelle molecole gassose
in atmosfera, l’espulsione di un
protone che viene sostituito dallo
stesso neutrone. Si formerà un
atomo con una carica in meno ma
stesso peso atomico.
0n
14
1 H
1
6C
1 H
1
Il 14C è un isotopo instabile e decade in 14N con un tempo di dimezzamento di 5730 ± 40 anni :
14
14
6C
14
7N
+
0
-1
β-
6C
14
7N
0
-1β
METODO DEL CARBONIO (radiocarbonio)
Nell’ atmosfera gli atomi di 14C formano velocemente 14CO2 combinandosi con ossigeno. Tale
molecola, che ha comportamento chimico simile alle molecole 13CO2 e 12CO2, si distribuisce
velocemente ed in maniera omogenea nell’atmosfera, a causa dei venti e della rotazione
terrestre. Lo scambio tra atmosfera ed idrosfera fa entrare rapidamente 14CO2 nei cicli biologici.
La 14CO2 viene assorbita direttamente con la fotosintesi nelle piante, e indirettamente tramite
processi metabolici negli animali erbivori e quindi carnivori attraverso la catena alimentare. In tal
modo il 14C viene distribuito in maniera omogenea nella biosfera. Il livello di concentrazione di 14C
si mantiene costante nel tempo nella biosfera poiché eguaglia quello perduto per decadimento,
quindi anche il rapporto 14C/12C sarà costante.
Al
momento
della
morte
dell’organismo, sia pianta o animale,
l’assorbimento di 14C dall’ambiente
cessa.
Quindi dal momento della morte la
concentrazione di 14C decresce, nel
tempo, nei tessuti di quell’organismo
per decadimento: l’orologio inizia a
funzionare, indipendentemente dalle
condizioni ambientali (parametri fisici
e chimici).
DATAZIONE CON 14C
Nell’ipotesi che la concentrazione iniziale ed attività di 14C nel campione siano uguali a quelle
moderne, quindi che non siano variate nel tempo, e che non vi siano contaminazioni post-mortem
(impurezze radioattive o 14C prodotto da bombe termonucleari), è possibile datare il nostro
campione conoscendo la costante di decadimento (o disintegrazione) per il radio nuclide 14C.
Infatti basterà introdurre i valori appropriati all’equazione: t = -1/λ
λ [ ln (N0/N(t))] per conoscere l’età
del materiale organico oggetto di analisi.
La datazione con il metodo del
radiocarbonio si esegue misurando
con spettrometro di massa il rapporto
14C/12C
nel campione e in uno
standard di riferimento cioè in un
materiale organico vegetale cresciuto
in assenza di contaminazione (creato
nel 1950). In tal modo il rapporto N0/Nt
sarà uguale al rapporto di 14C/12C
misurato nello standard (N0) e nel
campione(Nt)
Grafico dei tempi di decadimento del Carbonio-14. Il metodo basato sul carbonio radioattivo viene
utilizzato per la datazione di materiale contenente carbonio di origine organica vecchio fino a
50.000 anni, cioè tra il Pleistocene Superiore e l’Olocene.
DATAZIONE CON 14C
Il metodo della datazione con 14C presuppone che non vi siano fluttuazioni del rapporto 14C/12C
nel tempo. In effetti però sono stati individuati vari eventi quali, la variazione della radiazione
solare, variazioni climatiche, variazioni del campo magnetico terrestre e l’attività antropica che
hanno determinato una variazione della concentrazione di 14C nell’atmosfera e di conseguenza
nella biosfera e idrosfera. Sono stati quindi individuati metodi correttivi che devono essere
utilizzati per la calibrazione dell’età ottenuta con il metodo del radiocarbonio. Tale calibrazione al
momento risulta efficace fino a circa 24.000 anni dal presente.
In figura è riportata la variazione del
rapporto 14C/12C in atmosfera negli
ultimi 1000 anni. Le cause
dell’effetto De Vries non sono
conosciute, ma le cause dell’effetto
Suess sono imputabili a diluizione
del rapporto 14C/12C a causa
dell’immissione in atmosfera di
molta CO2 da combustione di
prodotti petroliferi. Notare infatti che
l’effetto Suess inizia alla fine del
1800.
METODO DEL K/Ar (POTASSIO-ARGON)
Tale metodo geocronologico è basato sulla misura della quantità del nuclide figlio (40Ar)
prodotto dal decadimento del nuclide radiogenico padre (40K).
Il potassio (K) ha tre isotopi che si trovano in percentuali diverse ma costanti in natura:
41K (6.73%), 40K (0.011%), 39K (93.25%).
Ar atmosferico ha 3 isotopi (40Ar, 38Ar, 36Ar) ma 40Ar = 99,6% è prodotto dal decadimento di 40K.
Il 40K è radiogenico e decade in tre modi diversi trasformandosi in:
40K+ 0 e
40Ar
1a.
(cattura di un elettrone) – 11.2% di 40K
-1
40K
40Ar + 0 β+ (emissione di un positrone) – 0.001% di 40K (raro)
1b.
1
40
40
0
2a.
K
Ca + -1β- (emissione di un elettrone) – 88.8% di 40K
Le costanti dei due principali metodi di decadimento sono:
λ1a = 5.81 x 1011 y (y = anni)
λ2a = 4.96 x 1010 y
λ (complessiva) = 5.543 x 1010 y
t1/2 (tempo di dimezzamento) =
ln 2
5,543 x 10-10
= 1,25 x 109 y = 1,25 Miliardi
essendo la frazione di atomi di 40K che decadono in 40Ar uguale a [(λ
λ1a/ λ)40K ] ne consegue che:
40Ar = (λ
λ1a/ λ)40K (eλt -1)
Da cui
λ1a/ λ)+1]
t = - (1/λ
λ) ln [40Ar/40K (λ
che può essere calcolata misurando la concentrazione residua di
accumulato nel minerale stesso.
40K
nel minerale e
40Ar
METODO DEL Rb/Sr (RUBIDIO-STRONZIO)
In natura si trovano due isotopi del rubidio:
85 Rb che costituisce il 72.17% ed il 87 Rb che costituisce il 27.83%.
37
37
Il 8737Rb è radiogenico e decade secondo la reazione:
87
37Rb
87
38Sr
+ 0-1β-
con λ = 1.42 x 10-11 e t1/2 = 48.8 x 109 anni
Quindi:
87Sr
rad
= 87Rb (eλt -1)
Lo Sr si trova in natura in quattro isotopi:
84
38Sr,
86
38Sr,
87
38Sr,
88
38Sr
i cui rapporti reciproci di concentrazione variano al variare del decadimento di 87Rb.
Il raggio ionico dello Sr (=1.13 Å) è simile a quello del calcio (=0.99 Å) e generalmente i due
elementi sono vicarianti, quindi lo Sr si trova disperso in molti minerali (specialmente plagioclasio,
apatite, calcite, aragonite) oltre a formare minerali propri. Quindi molti minerali all’atto della
cristallizzazione già contengono 87Sr non formatosi dal decadimento radioattivo di 87Rb nel
sistema di studio.
Nel calcolo quindi dell’età radiometrica del minerale, con il metodo Rb-Sr bisogna considerare
la presenza di 87Sr naturale.
Quindi la legge del decadimento radioattivo si può scrivere come:
87Sr
tot
=87Sri + 87Rb (eλt-1)
Quindi la legge del decadimento radioattivo si può scrivere come:
87Sr
tot
=87Sri + 87Rb (eλt-1)
Dove 87Srtot è la quantità totale di 87Sr al momento della misura e 87Sri (iniziale) è la quantità di
87Sr al momento della chiusura del sistema considerato.
Lo Sr naturale è costituito da 4 isotopi e il loro rapporto di concentrazione reciproca è noto:
87Sr/86Sr noto. Questo in prima approssimazione perché tale rapporto evolve nel tempo a
i
causa del continuo decadimento di 87Rb.
Nel caso in cui il sistema è rimasto chiuso nel tempo intercorso dalla formazione del minerale al
tempo di misura, il rapporto 87Sr/86Sri (iniziale) può essere misurato in minerali del sistema
considerato, che non contengano Rb. Questi sono ad esempio apatite e Ca-plagioclasio
(anortite). Si può quindi utilizzare 86Sr come numeratore dell’equazione precedente che diventa:
[87Sr/86Sr](tot) =[87Sr/86Sr] (i) + [87Rb/86Sr] (eλt-1)
Si può quindi misurare con la spettrometria di massa sia 87Sr/86Sr (tot), [nel minerale da datare];
che 87Sr/86Sri [nel minerale che non contiene Rb]; che 87Rb/86Sr [nel minerale da datare], e
lasciando come incognita solo t.
Per cui:
t = 1/λ ln [
(87Sr/86Sr (tot)- 87Sr/86Sr (i))
(87Rb/86Sr)
+ 1]
Nel caso in cui il la quantità di 87Sri od il rapporto 87Sr/86Sr (i) non può essere determinato, per
esempio perché il nostro sistema:
1) ha subito variazioni chimico-fisiche conseguenti ad un evento metamorfico,
2) non sono presenti minerali che non contengono Rb
il rapporto 87Sr/86Sr (i) può essere ottenuto per via grafica.
Infatti si può assumere che, essendo il tempo di dimezzamento di
confrontato con l’età della Terra, si può considerare:
87Rb
molto elevato anche se
eλt -1 = λt
87Sr
Quindi la legge del decadimento radioattivo:
87Sr
si può scrivere come :
rad
rad
= 87Rb (eλt-1)
= 87Rb λt
inserendo lo 86Sr al denominatore e considerando che nel sistema vi sia 87Sri
87Sr/86Sr
(tot)
= (87Sr/86Sr (i)) + (87Rb/86Sr) λt
Questa è l’equazione di una retta avente come coefficiente angolare (87Rb/86Sr) λ.
87Sr/86Sr
(tot)
= (87Sr/86Sr (i)) + (87Rb/86Sr) λt
In funzione della diversa quantità di 87Rb presente nelle fasi minerali costituenti il campione al
momento della chiusura del sistema e, del rapporto iniziale di 87Sr/86Sri otterremo rette con
pendenze diverse. Quindi analizzando fasi diverse in una stessa roccia o rocce diverse con la
stessa età ma contenuti di 87Rb diversi, si otterranno: 1) 87Rb/86Sr che moltiplicato per λ =
coef.ang.; 2) 87Sr/86Sr intercetta sul diagramma. Con questi dati misurati potremo tracciare varie
rette. Queste si intersecheranno in un punto corrispondente all’età di chiusura del sistema e al
rapporto iniziale di 87Sr/86Sr prima degli incrementi di 87Sr dovuti al decadimento di 87Rb.
(87Rb/86Sr) λ
In figura è riportato un esempio di
determinazione
dell’età
t(i)
e
della
composizione isotopica dello 87Sr(i) in una
roccia.
Tale determinazione è basata sulle misurazioni
del rapporto 87Sr/86Sr effettuate sia sulla roccia
totale che sulle single fasi separate. In ascissa
sono riportate le età in milioni di anni, in
ordinata i rapporti 87Sr/86Sr iniziali e misurati.
Da notare che il 87Sr/86Sr(i) = 87Sr/86Sr misurato
nell’apatite che non contiene rubidio. La diversa
pendenza delle rette dipende dalla quantità
iniziale di 87Rb nelle diverse fasi che produrrà
una maggiore quantità di 87Sr dal decadimento
radioattivo.
Da Fornaseri, 1980; modificata.
METODI DEL U-Pb (URANIO-PIOMBO) e Th-Pb (TORIO-PIOMBO)
Si applica a rocce contenenti isotopi dell’uranio (o torio) e del piombo. In natura esistono 4 isotopi
stabili: 204Pb, 206Pb, 207Pb e 208Pb. Di essi solo il 204Pb non è prodotto da decadimento radioattivo.
Quindi in una data roccia o minerale, il 204Pb è presente in quantità costante nel tempo. La sua
presenza in un sistema ci avverte che una parte del piombo non è radiogenica.
Al momento della formazione della crosta terrestre tutti gli isotopi del piombo sono presenti in una
certa proporzione, ma con il passare del tempo i decadimenti di:
238U
206Pb, 235U
207Pb,
e 232Th
208Pb,
arricchiscono il materiale terrestre di isotopi del piombo con conseguente aumento dei rapporti
206Pb/204Pb, 207Pb/204Pb e 208Pb/204Pb.
Per questo motivo la composizioni isotopica del piombo è in continua evoluzione e presenta
differenti composizioni in ere geologiche diverse. In tabella vengono riportate le abbondanze
isotopiche attuali e quelle al tempo di formazione della Terra (4.5 Ga) ricavate dallo studio di
meteoriti con contenuto di uranio molto piccolo.
Tabella: confronto tra le percentuali relative al 204Pb
degli isotopi del piombo al momento della formazione
della Terra ed oggi.
204Pb
206Pb
207Pb
208Pb
Oggi
1%
17.2%
15.8%
37.4%
T4.5 Ga
1%
4%
4.4%
12%
Determinazioni geocronologiche che utilizzano il decadimento di 232Th, 235U e 238U possono dare
risultati soddisfacenti qualora non si verifichino perdite episodiche di Pb o guadagno di U nelle fasi
minerali in cui si effettuano le misure.
Le leggi di decadimento delle famiglie di U e Th sono:
206Pb
= 238U (eλ1t -1)
207Pb = 235U (eλ2t -1)
208Pb = 232Th (eλ3t -1)
con λ1 = 1.15 x 10-10 y-1
con λ2 = 9.84 x 10-10 y-1
con λ3 = 4.94 10-11 y-1
I minerali contenenti questi isotopi generalmente contengono il piombo naturale 204Pb, isotopo
non radiogenico, il quale è presente anche in minerali che non contengono U e Th. Analogamente
al caso di Rb-Sr si possono trasformare le leggi di decadimento con al denominatore il 204Pb.
Il primo membro delle equazioni è il valore del rapporto isotopico misurato, il membro con la
denotazione “i” rappresenta il valore iniziale, alla chiusura del sistema, mentre l’ultimo membro
U/Pb e Th/Pb è il rapporto isotopico misurato.
Utilizzando questa serie di equazioni si otterranno tre datazioni indipendenti dello stesso
campione che in teoria dovrebbero coincidere.
Per i materiali geologici quali rocce e minerali si utilizzano i metodi riportati in tabella.
Ogni metodo fornisce risultati più attendibili se utilizzato nell’intervallo temporale
visualizzato.
Metodi di Radiodatazione
intervallo di tempo in
prodotti del
tempo di
radionuclidi
anni valido per la
decadimento dimezzamento
datazione
87Rb
87Sr
4,8·1010
4,5·109÷1010
232Th
208Pb 4He
1,39·1010
4,5·109÷107
238U
206Pb 4He
4,5·109
4,5·109÷107
235U
207Pb 4He
7,1·108
4,5 · 109÷107
40K
40Ar
1,33·109
4,5·109÷104
14C
14N
5,73·103
max 40·103
Datazione con 87Sr/86Sr di rocce sedimentarie
I sedimenti marini carbonatici di origine biologica
(non alterati) possono essere datati sula base del
loro rapporto isotopico 87Sr/86Sr.
Tale tecnica utilizza la variazione del rapporto
87Sr/86Sr nell’acqua marina da cui i carbonati
biologici si originano. L’omogeneizzazione del
87Sr/86Sr nell’acqua marina è rapido ed il suo
valore è uguale in tutti i mari interconnessi. La
variazione di 87Sr/86Sr nel tempo è rappresentata
dalla curva di Mc Arthur.
METODO DELLE TRACCE DI FISSIONE
Il metodo geocronologico delle tracce di fissione è basato sul rilevamento dei danni provocati alle
strutture cristalline da parte delle disintegrazioni radioattive conseguenti alla fissione di 238U. Le
impronte dei danni sono messe in evidenza con opportuni procedimenti chimici e vengono contate
servendosi del microscopio ottico. Il rapporto tra il numero di tracce di fissione vecchie (cioè già
presenti nel campione) e di tracce di fissione nuove (ottenute sottoponendo il campione a un
bombardamento con quantità note di 238U) corrisponde al tempo trascorso da quando il minerale
subì un certo raffreddamento. L’ampiezza degli intervalli misurabili con questo metodo va da
300.000 a 300 milioni d’anni.
Tracce di fissione in apatite
METODO DELLE VARVE
Il metodo geocronologico delle varve si basa sul conto delle alternanze stagionali di sedimenti
che costituiscono i deposti in laghi periglaciali. Ciascuno strato o varva* è composto di un livello
chiaro e uno scuro. La coppia di livelli rappresenta l’intervallo di tempo di un anno. Quindi il
numero di varve in un deposito ne definisce il tempo di formazione. Con questo metodo, nei
depositi glaciali scandinavi ed americani sono state datate delle sequenze che risalgono fino a
15.000 anni fa.
Lago periglaciale
Sedimenti varvati lacustri
*varva [deriva dallo svedese varv, deposito, passato in inglese come varve. Il termine fu introdotto dal
geologo scandinavo De Geer nel 1912],
DENDROCRONOLOGIA
Il metodo geocronologico della dendrocronologia si
basa sulla misura degli anelli annuali di accrescimento
delle piante, siano esse fossilizzate o non. Inoltre è
possibile trarre indicazioni sulle variazioni climatiche
basandosi sul presupposto che i vasi conduttori delle
piante si modificano secondo la maggiore o minore
presenza di acqua.
In primavera, per lo schiudersi delle gemme, è necessario un maggior
apporto idrico e le pareti dei vasi sono pertanto più sottili al fine di
permettere un flusso maggiore. Ogni stagione vegetale determina
inoltre un accrescimento del diametro del fusto con la formazione di
nuovo tessuto. Nella sezione trasversale di un tronco appariranno
quindi degli anelli annuali, ciascuno formato da una parte più chiara e
larga corrispondente al legno primaverile, e da una più scura e
compatta corrispondente al legno estivo.
La dendrocronologia non è applicabile agli alberi che vivono in aree
senza variazioni stagionali, dove l’accrescimento è costante tutto
l’anno, e neppure alle dicotiledoni, come le palme, in cui
l’accrescimento non avviene secondo anelli concentrici. Per stabilire
l’età di un albero senza abbatterlo si effettua un carotaggio, si preleva
cioè un tassello di legno corrispondente al raggio del tronco. La
dendrocronologia permette la datazione solo di periodi relativamente
recenti, vista la durata limitata della vita di una pianta e la scarsità di
reperti fossili.