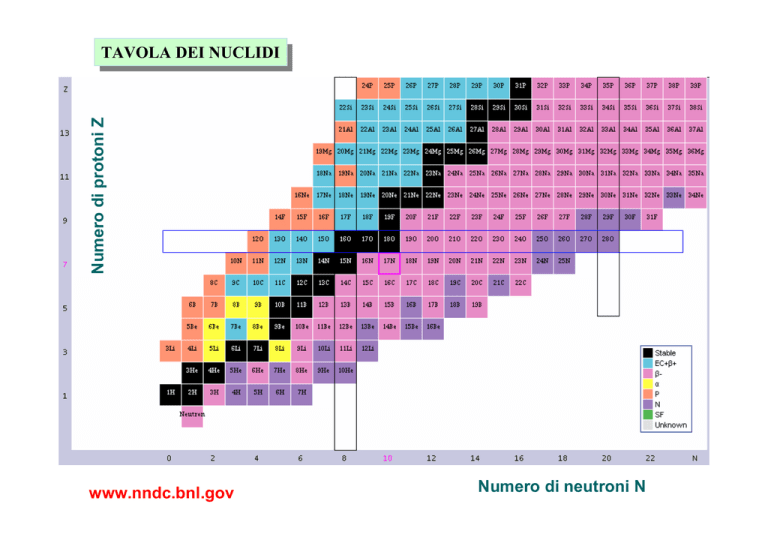
Numero di protoni Z
TAVOLA
TAVOLADEI
DEINUCLIDI
NUCLIDI
www.nndc.bnl.gov
Numero di neutroni N
TAVOLA
TAVOLADEI
DEINUCLIDI
NUCLIDI
www.nndc.bnl.gov
TAVOLA
TAVOLADEI
DEINUCLIDI
NUCLIDI
Con il termine nuclide si indicano tutti
gli isotopi conosciuti di elementi chimici
Numero di protoni Z
• Stabili:
279
• Instabili: ~ 5000
Con il termine radionuclide si indicano
tutti gli isotopi instabili che decadono emettendo
energia sotto forma di radiazioni (particelle e/o
radiazioni e.m.)
Numero di neutroni N
LA
LALEGGE
LEGGEDEL
DELDECADIMENTO
DECADIMENTORADIOATTIVO
RADIOATTIVO
L’istante esatto in cui un radionuclide decadrà non si può prevedere esattamente. Si può
tuttavia notare che il numero di decadimenti che avvengono in una sostanza radiaottiva rispetta
una legge statistica ben precisa.
Consideriamo una sostanza radioattiva contenente, ad un generico istante t, un numero N di
nuclei molto grande. Il numero di nuclei N che ci si aspetta che decadono in un intervallo t è
proporzionale all’intervallo di tempo e al numero N di nuclei presenti:
N N t
Il segno meno indica il fatto
che il numero di atomi
diminuisce nel tempo
è detta costante di decadimento, ha le dimensioni di un
inverso del tempo (s-1) e rappresenta una probabilità di
decadimento per unità di tempo, tanto maggiore è il suo
valore, tanto più alta è la probabilità di decadimento.
ESEMPIO:
Il valore della costante di
decadimento dipende in
modo critico dal
radionuclide considerato:
60Co
probabilità di 1/240 milioni di disintegrarsi in
un secondo ≈ 4 · 10-9 s-1
238U
probabilità di 1/(2·1017)
219Rn
probabilità di circa 1/6
≈ 5 · 10-18 s-1
≈ 0.17 s-1
Quanto maggiore è , tanto più elevata è la frequenza dei decadimenti
LA
LALEGGE
LEGGEDEL
DELDECADIMENTO
DECADIMENTORADIOATTIVO
RADIOATTIVO
dN N dt
1.5
N
1.4
1.3
N N0 e
Risolvendo l’equazione differenziale si ottiene la legge del
decadimento radioattivo:
t
dove si è indicato con N0 il numero di nuclei di cui
è costituito il campione radioattivo al tempo t=0:
1.2
1.1
N0
1.0
0.9
0.8
0.7
0.6
N0.5
0/2
1
vita media
0.4
N0/e
0.3
N0/4
0.2
0.1
0.0
0.0
0.5
T1/2
1.0
1.5
22.0T1/2
2.5
3.0
3.5
t4.0
Anche il valore del tempo di
dimezzamento (e vita media) dipende
ovviamente dal radionuclide considerato.
Esempio: a parità di elemento chimico:
219Th:
T1 2
ln 2
0.693
tempo di dimezzamento
tempo che deve trascorrere
affinché il numero di nuclei si
riduca della metà
T1/2 =10-6 secondi
232Th: T = 1010 anni
1/2
LA
LALEGGE
LEGGEDEL
DELDECADIMENTO
DECADIMENTORADIOATTIVO
RADIOATTIVO(dimostrazione)
(dimostrazione)
dN N dt
Separo le variabili
dN
dt
N
Integro ambo i membri
ln N t C
N e t C
C è una costante. Dalla definizione di logaritmo
Indicando con N0 il numero di nuclei di cui è costituito il
campione al tempo t=0 si ha:
N 0 e 0C e C
N e
t C
e e
C
Quindi:
t
N0 e
t
N N0 e
t
LA
LALEGGE
LEGGEDEL
DELDECADIMENTO
DECADIMENTORADIOATTIVO
RADIOATTIVO
Una grandezza che esprime la “velocità” di decadimento di
una data sostanza radioattiva è l’attività:
N
A
N
t
Essa esprime il numero di decadimenti in una unità di tempo.
Unità di misura nel S.I. Becquerel (Bq) 1 Bq equivale ad 1 disintegrazione al secondo
L’unità di misura originaria dell’attività, ormai “in disuso” è il Curie (Ci) 1 Ci = 3.7 × 1010 Bq
La legge di decadimento si può quindi esprimere anche in termini di attività:
1.5
A A0 e
t
A
1.4
1.3
1.2
1.1
A0
1.0
0.9
dove si è indicato con A0 l’attività
del campione al tempo t=0:
0.8
0.7
0.6
A00.5
/2
0.4
A0/e
0.3
A0/4
0.2
0.1
0.0
0.0
0.5
T1/2
1.0
1.5
22.0T1/2
2.5
3.0
3.5
t4.0
IL
ILTEMPO
TEMPODI
DIDIMEZZAMENTO
DIMEZZAMENTO
1
1
1
1
1
2
4
8 16
0
1
2
3
4
1
1
1
1
1
2
2
2
2
2
1
Trascorsi n tempi di dimezzamento, l’attività iniziale si è ridotta a:
2
n
CALCOLO
CALCOLODELL’ATTIVITA’
DELL’ATTIVITA’DI
DIUNA
UNASOSTANZA
SOSTANZARADIOATTIVA
RADIOATTIVA
Nota la massa m (grammi) di una sorgente radioattiva con costante di decadimento
, la sua attività è pari a:
m
A N NA
A
A è il numero di massa e NA il numero di Avogadro
ESEMPIO:
Calcolare l’attività di 1g di 226Ra sapendo che il tempo di dimezzamento è pari a 1600 anni.
Determinare inoltre il valore dell’attività dopo 3200 anni e dopo 2000 anni.
T12 1600 anni 5 1010 s
ln 2 m
AN
NA
T1/ 2 A
AN
0.693 1
23
10
6
.
02
10
3
.
7
10
Bq
10
5 10 226
Essendo il tempo di dimezzamento pari a 1600 anni, dopo 3200 anni (ossia dopo 2 tempi di
ln 2
dimezzamento) l’attività si sarà ridotta di un fattore 4:
2T1 / 2
A
T1 / 2
A(2 T1/ 2 ) A0 e
0 0.9 1010 Bq
4
L’attività dopo 2000 anni la si ricava dalla legge di decadimento:
A(2000 anni ) 3.6 1010 Bq e
ln 2
2000 anni
1600 anni
3.7 1010 Bq 0.42 1.6 1010 Bq
ESEMPI:
Calcolare l’attività di 40K in una banana, sapendo che essa contiene 525 mg di potassio.
(T1/2 del 40K =1.26 109 anni, percentuale isotopica 40K : 0.01%)
T12 1.26 109 anni 4 1016 s
AN
ln 2 m
NA
T1/ 2 A
m è la massa (in grammi) del solo 40K. E’ pari
allo 0.01% della massa totale di K
m 525 10 3 g
0.01
525 10 7 g
100
0.693 525 10 7
23
A
6
.
02
10
14 Bq
16
4 10
40
Nel corpo umano di un adulto vi sono circa 160 grammi di potassio, contenuti essenzialmente nelle
ossa. E’ quindi una sorgente naturale di 40K la cui attività è:
0.693 160 10 4 g
23
A
6
.
02
10
4000 Bq
16
4 10 s
40
ESEMPIO:
Un rivelatore di radiazione sta misurando un'attività di 2000 Bq. Sapendo che il campione
radioattivo è costituito da isotopi di 131I il cui tempo di dimezzamento è di 8 giorni, si chiede quale
era la sua attività 40 giorni fa. Si chiede inoltre quanto tempo occorre aspettare affinché l'attività si
riduca a 100 Bq.
t
A0 2000 e
A A0 e t A0 A e
ln 2
40
8
64000 Bq
In effetti 40 giorni corrispondono a 5 tempi di dimezzamento e si ritrova che:
1
A(5T1/ 2 ) A0
2
5
5
1
2000 Bq 64000 Bq
2
A
T1/ 2 A0
1 A0
A
t
ln
e ln t t ln t
A
ln 2 A
A0
A0
T1/ 2 A0
8
2000
t
ln
ln
35 giorni
ln 2 A ln 2 100












