Definizione di probabilità

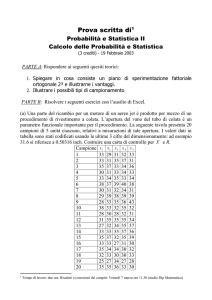
Considerato un esperimento (fenomeno
aleatorio): ad esempio, il lancio di un dado a
6 facce, indichiamo con Ω l’insieme di tutte
le uscite possibili: Ω ={1,2,3,4,5,6}
Si definisce evento ogni sottoinsieme di Ω.
I sottoinsiemi che contengono un solo
elemento si chiamano eventi elementari.
Esempio. {1} indica l’evento “esce 1”.
Ω indica l’evento certo e ∅ indica l’evento
impossibile.
Se E∩F=∅, si dice che i due eventi sono
incompatibili.
Si dice che un evento E si è verificato
quando l’esito della situazione aleatoria
(esperimento) che si considera
appartiene a E.
Quindi, l’evento “si verifica l’evento A
oppure l’evento B” si rappresenta con
A∪B.
Mentre l’evento “si verifica l’evento A e
l’evento B” si rappresenta con A∩B.
∨
1
2
3
L’insieme di tutte le possibili uscite
dell’esperimento si chiama anche spazio di
probabilità.
Decidiamo che
la probabilità dell’evento certo è 1, che
la probabilità è additiva rispetto ad eventi
incompatibili e
che la probabilità dell’evento impossibile è 0.
Allora se lo spazio di probabilità ha n
elementi (cioè, gli eventi elementari sono in
numero finito) e sono equiprobabili allora
4
Elencare gli elementi che appartengono ai
seguenti eventi:
•L’evento che si verifichi esattamente 0
degli eventi A e B
•L’evento che si verifichi esattamente 1
degli eventi A e B
•L’evento che si verifichi almeno 1 degli
eventi A e B
essendo A={1,2,3,4,5,6} e B={4,5,6,7,8,9}
Definizione di probabilità
necessariamente la probabilità di ciascun
evento elementare è uguale a 1/n.
Esempio:
Esperimento: lancio del dado equo
Spazio di probabilità: {1,2,3,4,5,6}
Eventi elementari equiprobabili:
P({1})= P({2})= ….=P({6})= 1/6
Poiché la probabilità è additiva sugli eventi
incompatibili, allora si ha
Nel caso di eventi elementari equiprobabili e
finiti è possibile dimostrare che ripetendo
l’esperimento un numero N molto grande di
volte il rapporto fE /N fra il numero di volte fE
in cui si è verificato l’evento E ed N,
approssima P(E), ovvero
fE/N→ P(E), quando N tende all’infinito.
P({1,3})= P({1}∪ {3})= 1/6+1/6=2/6=1/3
5
6
1
Assiomi di Kolmogorov
Ne segue che se disponiamo degli esiti di N
La probabilità è una funzione P definita su P(Ω)
a valori in [0,1] tale che valgano le seguenti
proprietà:
ripetizioni di un esperimento, la frequenza
relativa osservata dell’evento E può essere
1. P(Ω)=1,
2. se A e B sono due insiemi disgiunti, allora
P(A∪B)=P(A)+P(B), additività sugli insiemi
disgiunti.
usata come un’approssimazione della
probabilità P(E). Questa approssimazione è
chiamata probabilità empirica.
7
Proprietà
Ω viene chiamato spazio campionario o spazio di
8
probabilità o spazio campione.
Si noti che per un dato esperimento aleatorio,
possono essere definite molte misure di
1. P(¬A)=1-P(A),
2. P(∅)=0,
probabilità.
3. P(A \ B)=P(A)-P(B), se B ⊆ A,
Per “misura” o “distribuzione” di probabilità
4. se B ⊆ A, allora P(B) ≤ P(A),
intendiamo una regola che ci consenta di
5. P(A \ B)=P(A)-P(A ∩ B),
assegnare i valori di probabilità agli eventi
6. P(A∪B)= P(A)+ P(B)- P(A ∩ B).
elementari di uno spazio campione in maniera
9
Distribuzione uniforme
tale da soddisfare gli assiomi di Kolmogorov. 10
Nel caso del dado osserviamo che:
1
P( Ei ) = , ∀i = 1,6
6
Per uno spazio campione finito Ω, la più
più
importante distribuzione di probabilità
probabilità è la
distribuzione uniforme:
P(A)=⏐
P(A)=⏐A⏐/⏐Ω⏐,
⏐Ω⏐,
Dove ⏐A⏐= numero di elementi di A e ⏐Ω⏐=
⏐Ω⏐=
numero di elementi di Ω.
Quindi lo stesso valore viene assegnato a ogni
punto dello spazio campionario.
11
P( Ei ) ≥ 0, ∀i = 1,6
6
∑ P( Ei ) = 1
i=1
12
2
Lancio di 2 dadi
Evento:
Evento: ‘esce un numero dispari’
dispari’
Possibili esiti che appartengono all’
all’evento:
evento
Si lanciano due dadi equi a sei facce uno rosso e
uno bianco e si sommano i numeri risultanti
sulle facce superiori. Determinare lo spazio
degli eventi e calcolare la probabilità
probabilità che la
somma sia 5, e poi che la somma sia 12. Di tutte
le somme possibili qual è la più
più probabile?
L’evento è composto di 3 esiti.
Evento:
Evento: ‘esce il numero 2’
2’
Un solo esito possibile appartiene a questo
evento: è un evento elementare.
Ω = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1),
(2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3),
(3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5),
(4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1),
(6,2), (6,3), (6,4), (6,5), (6,6)}.
13
14
Esempio
Consideriamo l'esperimento costituito
dall'estrazione di una pallina da un’
un’urna
contenente 10 palline. Di queste, 5 sono
bianche, 3 rosse e 2 nere.
Definiamo 3 eventi complessi:
A =estrazione di una pallina bianca
B =estrazione di una pallina rossa
C =estrazione di una pallina nera.
Ciascuno di questi 3 eventi costituisce un
sottoinsieme dello spazio campione Ω.
15
3