L'enigma dei numeri primi
Bardonecchia 16-18 Dicembre 2016
Introduzione
I numeri primi:
●
sono un concetto semplice;
●
ruolo fondamentale nella vita di tutti i giorni;
●
stanno lasciando una lunga scia di congetture.
Introduzione
“Dio creò i primi 10 numeri, il resto è opera dell'uomo.”
Leopold Kronecker (1823-1891)
Introduzione
Introduzione
Introduzione
Sistemi di numerazione:
●
additivo;
●
posizionale.
Cosa sono i numeri primi
Teorema di divisibilità:
∀(a; b) ∈ NxN, b › 0 ∃! (q; r) ∈ NxN t.c. a = bq + r
con 0 ≤ r ‹ b.
I numeri q, r vengono detti rispettivamente quoziente
e resto della divisione di a per b.
Se r = 0 allora b divide a, cioè a è divisibile per b.
Cosa sono i numeri primi
Definizione di divisibilità:
Dati a, b ∈ Z (b≠0), si dice che b divide a, o che a
è divisibile per b, se ∃ c ∈ Z t.c. a=bc.
es. 4 divide 12 perché ∃ 3 t.c. 12=4·3
Cosa sono i numeri primi
I criteri di divisibilità:
●
per 2
deve essere pari;
●
per 4
le ultime due cifre devono essere un
multiplo di 4 oppure 00;
●
per 5
deve terminare per 5 o 0;
●
per 10 deve terminare per 0;
dim
Cosa sono i numeri primi
dim
I criteri di divisibilità:
●
per 3
la somma delle cifre deve essere un
multiplo di 3;
●
per 7
il numero che si ottiene sottraendo il
doppio dell'ultima cifra al numero senza
l'ultima cifra deve essere un multiplo di 7;
●
per 11 la differenza tra la somma delle cifre di
posto dispari e la somma delle cifre di
posto pari deve essere un multiplo di 11.
Cosa sono i numeri primi
Definizione di numero primo:
Un numero p ∈ N è primo se: p › 1 e se gli unici
divisori di p sono quelli banali (cioè 1 e p).
In altre parole:
p è primo ⇔ #Div(p) = 2.
Cosa sono i numeri primi
Crivello di Eratostene (273-194 a.C.)
Cosa sono i numeri primi
Crivello di Eratostene (273-194 a.C.)
Cosa sono i numeri primi
Crivello di Eratostene (273-194 a.C.)
Cosa sono i numeri primi
Crivello di Eratostene (273-194 a.C.)
Cosa sono i numeri primi
Crivello di Eratostene (273-194 a.C.)
Cosa sono i numeri primi
Crivello di Eratostene (273-194 a.C.)
Cosa sono i numeri primi
Come fare a decidere se un numero n è primo?
Algoritmo brutale:
●
●
●
dividiamo n per tutti i numeri m ∈ [2;n-1];
se ∀m la divisione non è possibile, allora n è
primo;
se ∃m per cui la divisione è possibile
(n = m·t; t ∈ N), allora n non è primo.
Cosa sono i numeri primi
Come fare a decidere se un numero n è primo?
Algoritmo meno brutale:
●
●
●
dividiamo n per tutti i numeri m ∈ [2;√n];
se ∀m la divisione non è possibile, allora n è
primo;
se ∃m per cui la divisione è possibile
(n = m·t; t ∈ N), allora n non è primo.
Cosa sono i numeri primi
Crivello geometrico
Cosa sono i numeri primi
dim
Teorema fondamentale dell'aritmetica
“Ogni numero n › 1 si scrive in modo unico come
un prodotto di numeri primi.”
In altri termini:
con i numeri primi si possono ottenere tutti gli altri
numeri; i numeri primi sono i "mattoni" dell’aritmetica.
Quanti sono i numeri primi
Teorema:
“I numeri primi sono infiniti.”
Dimostrazioni:
●
Euclide
per assurdo
●
Eulero
utilizza le serie
Quanti sono i numeri primi
Euclide (323-283 a.C.)
dim
Quanti sono i numeri primi
Come rappresentare una successione
●
●
an:
Forma analitica: permette di ricavare l'n-esimo
termine direttamente da n.
Forma ricorsiva:ricavo l'n-esimo termine
conoscendo i precedenti.
Quanti sono i numeri primi
Esempio: successione dei numeri pari
●
Forma analitica:
an = 2n
●
Forma ricorsiva:
a0 = 0
an = an-1 + 2
Quanti sono i numeri primi
Prova tu!
Rappresenta in modo
successioni di numeri:
ricorsivo
●
1, 3, 5, 7, 9, 11, 13, …
●
0, 3, 8, 15, 24, 35, 48, …
●
2/4, 5/7, 10/12, ...
le
seguenti
Quanti sono i numeri primi
Prova tu! soluzioni
Rappresenta in modo
successioni di numeri:
ricorsivo
●
1, 3, 5, 7, 9, 11, 13, …
2n+1
●
0, 3, 8, 15, 24, 35, 48, … n^2-1
●
2/4, 5/7, 10/12, …
le
seguenti
(n^2+1)/(n^2+3)
Quanti sono i numeri primi
Serie geometrica:
Lo strano parcheggio: un parcheggio ha le seguenti tariffe:
prima ora: 1 euro
seconda ora: 1/2 euro
terza ora: 1/4 euro
quarta ora: 1/8 euro
………ecc…………………...
Quanto dovrò pagare per lasciare parcheggiata l’auto per sempre?
Quanti sono i numeri primi
Leonhard Euler (1707-1783 d.C.)
dim
Quanti sono i numeri primi
Grandi lacune
Osserviamo i numeri primi fra i primi 100 numeri:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41,
43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Osserviamo i numeri primi da 100 a 200:
101, 103, 107, 109, 113, 119, 127, 131,
137, 139, 149, 151, 157, 163, 167, 173,
179, 181, 191, 193, 197, 199
Quanti sono i numeri primi
dim
Possono esserci lacune molto grandi, come, ad
esempio, cinquantamila numeri successivi fra i
quali non ci sia neppure un numero primo?
Quanti sono i numeri primi
Per secoli i matematici hanno dedicato il loro
tempo alla ricerca di una regola per descrivere i
numeri primi.
Ma se non si possono descrivere tutti, almeno
studiamo il comportamento di alcuni di essi.......
Quanti sono i numeri primi
Due numeri primi si dicono gemelli se differiscono
di due unità.
(p, p+2)
dove sia p che p+2 sono primi.
es. (3, 5), (17, 19), (71, 73), (281, 283)
Quanti sono i numeri primi
Congetture (da dimostrare):
●
“I numeri primi gemelli sono infiniti”
Euclide (300 a.C. ca.)
●
“Per ogni numero naturale k, esistono infinite
coppie di numeri primi che differiscano di 2k”
Alphonse De Polignac (1849)
Logaritmi e numeri primi
Logaritmi:
●
uno degli strumenti matematici più potenti;
●
nati come strumenti di calcolo (John Napier);
●
grazie a Gauss fondamentali nello studio dei
numeri primi.
Logaritmi e numeri primi
Napeir-Nepair-Nepier-Neper-Napare-Naper-...
John Napier (1550-1617)
Giovanni Nepero
Logaritmi e numeri primi
Logaritmi introdotti per semplificare i calcoli:
le moltiplicazioni diventano somme (di esponenti).
1.000 · 10.000 · 100.000 = 1.000.000.000.000= 1012 = 103+4+5
1.000 = 103
10.000 = 104
100.000 = 105
...
log = log10
log 1.000 = 3
log 10.000 = 4
log 100.000 = 5
e =2,71828 18284 59... ...
ln = loge
Logaritmi e numeri primi
progressione geometrica
x
log x
1 10 100 1.000 10.000 100.000 1.000.000
0 1
2
3
4
5
6
progressione aritmetica
progressione geometrica
x
log2 x
1
0
2
1
4
2
progressione aritmetica
8
3
16
4
32
5
64
6
Grafico e proprietà
Logaritmi e numeri primi
Definizione:
Il logaritmo in base a di b è quel numero al quale
dobbiamo elevare a per ottenere b.
loga b = c
⇔ ac = b
Logaritmi e numeri primi
Carl Friedrich Gauss (1777-1855)
Logaritmi e numeri primi
Numeri primi
minori di a (=∞) a/la
Logaritmi e numeri primi
Gauss:
●
non cerca la formula dei numeri primi;
●
studia la loro frequenza di apparizione;
●
introduce la funzione:
π(x)=quantità di numeri primi minori di x
Logaritmi e numeri primi
x
10
100
1.000
10.000
100.000
1.000.000
10.000.000
100.000.000
1.000.000.000
10.000.000.000
π(x)
4
25
168
1.229
9.592
78.498
664.579
5.761.455
50.847.534
455.052.512
Logaritmi e numeri primi
500000000
450000000
400000000
350000000
π(x)
300000000
250000000
200000000
150000000
100000000
50000000
0
10
100
1.000
10.000
1.000.000
100.000
x
10.000.000
100.000.000
10.000.000.000
1.000.000.000
Logaritmi e numeri primi
x
10
100
1.000
10.000
100.000
1.000.000
10.000.000
100.000.000
1.000.000.000
10.000.000.000
π(x)
4
25
168
1.229
9.592
78.498
664.579
5.761.455
50.847.534
455.052.512
π(x) / x
0,40000000
0,25000000
0,16800000
0,12290000
0,09592000
0,07849800
0,06645790
0,05761455
0,05084753
0,04550525
Logaritmi e numeri primi
0,45
0,4
0,35
0,3
π(x) / x
0,25
0,2
0,15
0,1
0,05
0
10
100
1.000
10.000
100.000
1.000.000
x
10.000.000
100.000.000
1.000.000.000 10.000.000.000
Logaritmi e numeri primi
x
10
100
1.000
10.000
100.000
1.000.000
10.000.000
100.000.000
1.000.000.000
10.000.000.000
Serie geometrica
π(x)
4
25
168
1.229
9.592
78.498
664.579
5.761.455
50.847.534
455.052.512
x / π(x)
2,5
4
6
8,1
10,4
12,7
15
17,4
19,2
22
Serie aritmetica
+2
Logaritmi e numeri primi
Congettura di Gauss:
x
Per valori grandi di x, il valore
si approssima
π(x)
bene con ln x.
x
π(x)
≈ ln x
cioè
π(x) ≈
x
ln x
Logaritmi e numeri primi
25
20
15
x / п(x)
ln x
10
5
0
10
100
1.000
10.000
100.000
1.000.000
x
10.000.000
100.000.000
10.000.000.000
1.000.000.000
Logaritmi e numeri primi
Quanti numeri primi ci sono tra 1 e 1000?
●
calcoliamo ln 1000;
●
invertiamo il numero ottenuto (1/x);
●
moltiplichiamo per 1000.
Si ottiene 144,76482... il numero esatto è 168!
Logaritmi e numeri primi
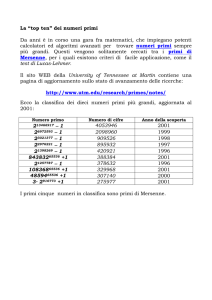
Numeri primi
minori di a (=∞) a/la
scriveva a 14 anni
Grandi matematici a confronto
Martin Mersenne (1588 - 1648)
Grandi matematici a confronto
dim
Numeri di Mersenne:
Mp = 2p -1
con p ∈ N, p primo
N.B. Non per ogni p primo risulta che Mp è primo.
Si può dimostrare che: Mp primo ⇒ p primo
Grandi matematici a confronto
Mersenne afferma che tra 2 e 2257, il numero Mp
è primo solo per i seguenti esponenti:
●
2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257
Nel 1947 si riuscì a completare la lista:
●
2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127
Grandi matematici a confronto
I primi dodici numeri primi di Mersenne sono:
M2 = 3
M7 = 127
M3 = 7
M5 = 31
M13 = 8191
M17 = 131071
M19 = 524287
M31 = 2147483647
M61 = 2305843009213693951
M89 = 618970019642690137449562111
M107 = 230584300921369391578010288127
M127= 170141183460469231731687303715884105727
Grandi matematici a confronto
●
●
●
●
i primi dodici numeri primi di Mersenne sono stati
scoperti prima del XX secolo;
i calcolatori elettronici hanno notevolmente
accelerato la scoperta dei primi di Mersenne;
alla fine del millennio i primi di Mersenne conosciuti
erano 38; oggi invece se ne conoscono 49.
il più grande numero primo conosciuto (a gennaio
2016) è M74207281. È stato calcolato da un
computer della University of Central Missouri, ha
più di 22 milioni di cifre.
Grandi matematici a confronto
Curiosità:
●
se scritti in base 2, tutti i numeri primi di Mersenne
sono rappresentati da stringhe di p cifre unitarie,
dove p è l'esponente primo di Mersenne.
310 = 112
710 = 1112
3110 = 111112
12710 = 11111112
819110 = 11111111111112
Grandi matematici a confronto
Pierre de Fermat (1601 - 1665)
Grandi matematici a confronto
dim
Piccolo teorema di Fermat:
se p è un numero primo, ed a è un intero positivo
qualunque, allora il numero
ap-a
è divisibile per p.
Cioè:
ap ≡ a (mod p)
Grandi matematici a confronto
Congettura di Goldbach:
“Tutti i numeri pari maggiori di 2 possono scriversi
come la somma di due numeri primi.”
...ancora da dimostrare!
Numeri primi e crittografia
“Tecnica di rappresentazione di un messaggio in una
forma tale che l’informazione in esso contenuta possa
essere recepita solo dal destinatario.”
Numeri primi e crittografia
Obiettivo: far arrivare messaggi a destinazione nel
modo più veloce, economico e sicuro possibile.
informazione confidenziale
trascurare economia e velocità
spedizione per segretezza
metodo
più
comune
mascherare il messaggio
Numeri primi e crittografia
La protezione dell'informazione ha origini antiche
Numeri primi e crittografia
●
●
●
le chiavi crittografiche sono diventate sempre più
lunghe;
i meccanismi per decifrare sempre più complessi;
Enigma ci insegna che il problema principale è la
trasmissione della chiave;
...e se la chiave fosse pubblica?
Numeri primi e crittografia
Cifrari RSA:
●
Alice e Bob scelgono un numero naturale n
●
Alice sceglie un numero a e Bob un numero b
●
Alice comunica a Bob il numero na
●
Bob comunica ad Alice il numero nb
●
Entrambi useranno nab come chiave
Numeri primi e crittografia
Sia n = ab, stimiamo il numero di tentativi per
scoprire a e b usando il teorema della radice
quadrata.
Sappiamo che un fattore (ad esempio a) soddisfa
allora vi sono approssimativamente
numeri primi da testare come divisori di n.
Numeri primi e crittografia
Se n ≈ 1050 (quindi un numero di 50 cifre) allora
e i tentativi sono
Per un computer capace di effettuare 1000
miliardi di test al secondo sono necessari più di
1.7 · 1011 secondi, ossia circa 5600 anni!
Numeri primi e crittografia
Prova di fattorizzazione con maple 9 su pentium
4, 2.60 Ghz.
Numeri primi e crittografia
Tempo di fattorizzazione T in funzione della
lunghezza l del numero:
T = 0.0005·e0.285l s
Dal risultato precedente per l = 300 (RSA) si
ottiene
T ≈ 1026 s che è maggiore dell'età dell’ Universo.
Numeri primi e crittografia
Funzione φ di Eulero:
per ogni intero positivo n, determina il numero degli
interi compresi tra 1 e n che sono coprimi con n.
Ad esempio φ(8) = 4 perché i numeri minori di 8
e primi con 8 sono 1, 3, 5, 7.
Numeri primi e crittografia
Teorema di Eulero ( teorema di Fermat-Eulero)
Se n è un intero positivo ed a è coprimo rispetto
ad n, allora:
aφ(n)≡1
(mod n)
Numeri primi e crittografia
Applicazione:
ricerca dell'ultima cifra di 7222 cioè di 7222 mod 10.
●
7 e 10 sono coprimi;
●
Φ(10) = 4;
●
per il teorema 74≡1 (mod 10);
●
Allora:
7222 = 74·55+2 = (74)55 · 72 = (1)55 · 49=49= 9
(mod 10)
Numeri primi e crittografia
Algoritmo RSA (1977 Rivest-Shamir-Adleman):
●
Si scelgono due numeri primi p e q e si calcola n = pq
●
Si calcola φ(n) = φ(pq) = φ(p)·φ(q)=(p-1)(q-1)
●
Si sceglie un valore e
●
Si calcola d tale che ed ≡1 mod φ(n)
‹
φ(n) coprimo con φ(n)
La coppia (e, n) costituisce la chiave pubblica, la
coppia (d, n) costituisce la chiave privata.
Numeri primi e crittografia
Numeri primi e crittografia
L'enigma dei numeri primi
Grazie per l'attenzione