caricato da
common.user11004
Choco-Math: Laboratorio Interattivo di Matematica

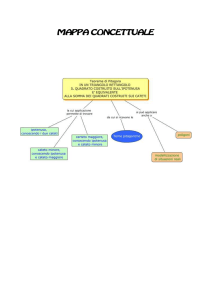
Choco-Math Introduzione Choco-Math è un piccolo laboratorio interattivo che utilizzando la cioccolata illustra in modo leggero e accattivante alcuni argomenti di matematica noti e meno noti. Il laboratorio introduce ai vari temi attraverso specifiche attività. Choco-Math è rivolto un pubblico vasto che va dal bambino all’adulto. Unici requisiti richiesti sono la curiosità scientifica e l’amore per la cioccolata. L’installazione utilizzerà in maniera preferenziale cioccolata proveniente dalla filiera del commercio equo e solidale. Elenco delle attività 1. 2. 3. 4. 5. 6. 7. Il Chomp e la teoria dei giochi. Il paradosso dell'area scomparsa: come creare cioccolata dal nulla. Terne pitagoriche. La serie armonica: la torre sporgente. Il teorema di Pick. Il problema della scacchiera mutilata. I numeri figurati Descrizione delle attività 1. Il Chomp e la teoria dei giochi Il Chomp [1] è la sfida tra due contendenti che devono, ad ogni mossa, mangiare almeno un quadratino di cioccolato. Chi mangia il quadratino avvelenato in basso a sinistra perde; vince quindi chi obbliga l’avversario a mangiare il veleno. La regola è che i giocatori hanno una bocca rettangolare: volendo mangiare un certo quadratino, il giocatore mangerà anche tutti quelli che si trovano più a destra e più in alto di esso. Per chiarire bene come funziona, proviamo a seguire una partita di Chomp. Il primo giocatore sceglie il quadratino che si trova nella terza colonna da destra e nella seconda riga dall’alto e mangia 6 quadratini. Il rettangolo del suo morso è quindi determinato dalla scelta del quadratino in basso a sinistra. Il secondo giocatore risponde con una mossa in cui mangia due soli quadratini: infatti sceglie il quadratino nella seconda riga dal basso e nella seconda colonna da destra, determinando così il “morso” rettangolare che è tratteggiato nella figura. Questo morso ha l’effetto pratico di togliere i due quadratini marcati in grigio perché il resto era già stato mangiato nella prima mossa. Il giocatore che aveva cominciato sceglie il quadratino appena sopra quello avvelenato, e si fa una scorpacciata di ben 7 quadratini: ma egli si accorge di avere in pratica regalato la vittoria all’avversario; e infatti, mangiando tutta la cioccolata “sana” dell’ultima riga, il secondo giocatore costringe l’avversario alla sconfitta. Il gioco del Chomp si presta ad interessanti analisi nell’ambito della teoria dei giochi [1] [2] [3]. Si dimostra ad esempio che esiste una strategia vincente per il primo giocatore ma solo in alcuni casi particolari è possibile descriverla. Il Chomp 1×n. Se la configurazione di partenza è una tavoletta 1×n come in figura è banale notare che il primo giocatore vince alla prima mossa Il Chomp 2×n. Se la configurazione di partenza è una tavoletta 2×n come in figura: la strategia del primo giocatore è togliere il quadretto in alto a destra raggiungendo una configurazione a “scalino”; ora, qualsiasi sia la risposta del secondo giocatore, alla terza mossa chi ha cominciato può sempre ricreare per il secondo giocatore la configurazione a “scalino”, per un Chomp più piccolo e così via, fino alla configurazione e a quella perdente: Il Chomp n×n. Se la configurazione di partenza è una tavoletta quadrata n×n , la strategia del primo giocatore consiste nel togliere il quadretto immediatamente sopra e a destra rispetto quello avvelenato: e poi proseguire “copiando” ogni volta la mossa del secondo giocatore (questa strategia prende il nome di “strategia simmetrica”). Attività Il visitatore verrà invitato a giocare a Chomp con tavolette formate da quadretti di cioccolata vera, o con modelli realizzati con materiali plastici, o ancora con apposite applicazioni per pc e tablet. L’animatore avrà quindi la possibilità di illustrare gli aspetti teorici legati alle strategie di gioco. 2. Il paradosso dell'area scomparsa: come creare cioccolata dal nulla Il paradosso dell'area scomparsa è un paradosso geometrico in cui la ridisposizione di una serie di tessere per semplice traslazione e rotazione sembra modificare la superficie totale delle tessere. Esistono diverse varianti di questo paradosso. Un esempio classico è il paradosso del cuneo. Le due figure sono composte dalle stesse tessere di uguale superficie, come si può constatare contando i quadrati della griglia. Due triangoli con base ed altezza identiche hanno la stessa area. Ci si trova nella situazione paradossale in cui la somma di quantità uguali dà risultati differenti. In realtà, le due figure non sono davvero triangoli, ma sembrano tali per un effetto ottico; la prima è, di fatto, un quadrilatero, e similmente la seconda (oltre al quadratino "vuoto"). Secondo Martin Gardner il rompicapo espresso in questa forma fu inventato nel 1953 da Paul Curry, un prestigiatore di New York City, universalmente noto per essere l'autore di uno dei più semplici e straordinari giochi di prestigio con le carte, il celebre Out of this world. Nonostante questo, il principio delle evanescenze geometriche è da tempo conosciuto. Il primo esempio di area che sparisce risale al 1566 e compare nel Libro d’Architettura Primo di Sebastiano Serlio (1475-1554), un architetto del Rinascimento. Mariano Tomatis ha utilizzato il paradosso dell’area scomparsa per creare l’illusione della creazione del cioccolato dal nulla [5] Si parte da una tavoletta di cioccolato, chiamiamola T, formata da 6 righe da 4 quadretti l’una. L’area totale è quindi di 24. Ora tagliamo la tavoletta, eliminiamo il quadretto e riassembliamo la tavoletta come indicato Otteniamo una nuova tavoletta che chiamiamo T’. Quelle che ci si aspetta è che l’area di T’ sia diminuita di 1 e valga quindi 23, in realtà, guardandola, sembra che l’area sia rimasta ancora 24. Ma questo non è vero! Se si osserva con attenzione, l’altezza di T’ è leggermente inferiore a quella di T. Questo accade perché la terza riga dal basso ha perso una superficie pari all’area del quadretto che abbiamo eliminato, e quindi ha area 3 e non più 4. Questa perdita si nota poco perché la superficie persa viene spalmata orizzontalmente. L’altezza della riga in questione è diminuita ma la larghezza è rimasta identica. Se chiamiamo h l’altezza della riga normale, e h’ quella della riga rimpicciolita in T’, vale la seguente relazione: h' 3 h 4 La riga “dimagrita” di T’ è alta il 25% in meno rispetto a prima. La nuova tavoletta T’ è larga come T, ha area 23, e la sua altezza vale 5 h + 3/4 h = 5,75 h, ovvero il 4% in meno. Attività Si mostrerà al visitatore come ottenere apparentemente (!) cioccolata dal nulla, svelando poi il trucco tramite una tavoletta di cioccolata formata da 3 righe da 10 quadretti. Si tratta di una variante del trucco di Tomatis nella quale la diminuzione di altezza della tavoletta è meno evidente. Nel nostro caso infatti la relazione tra l’altezza della riga normale h e quella della riga rimpicciolita h’ è: 9 h' h 10 E’ previsto anche l’analisi di diverse configurazioni utilizzando anche modelli di plastica e animazioni al computer con software di geometria dinamica 3. Terne pitagoriche ll teorema di Pitagora Il teorema di Pitagora afferma che: In ogni triangolo rettangolo il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti. In Algebra, il teorema di Pitagora si può esprimere così: Se a e b sono le lunghezze dei cateti di un triangolo rettangolo e c è la lunghezza dell'ipotenusa, si ha che: a2 + b2 = c2 Terne pitagoriche. Se tre numeri interi a, b e c verificano la relazione a2 + b2 = c2, si dice che formano una terna pitagorica. Ad esempio (3, 4, 5) e (5, 12, 13) sono due notissime terne pitagoriche, mentre non lo è (1, 1, 2) perché l'ultimo numero non è intero. Anche (6, 8, 10) è una terna pitagorica, ottenuta raddoppiando i termini della (3, 4, 5). Terne pitagoriche primitive e terne derivate. Le terne come la (3, 4, 5) sono dette terne primitive e quelle come la (6, 8, 10) sono dette derivate. Infatti, se (a, b, c) è una terna pitagorica, lo è anche (ka, kb, kc), con k numero intero positivo. Come si distinguono le terne primitive da quelle derivate? Semplice: se a e b sono primi fra loro allora la terna è primitiva, altrimenti è derivata. Alcune osservazioni, in ordine sparso In tutte le terne pitagoriche: - uno dei tre "lati" a, b, c è divisibile per 3 e un altro per 5 - il prodotto dei due "cateti" a×b è divisibile per 12 - il prodotto dei tre "lati" a×b×c è divisibile per 60 Nelle terne pitagoriche primitive: - uno dei due "cateti" a oppure b è pari e l'altro dispari, mentre l'"ipotenusa" c è sempre dispari - a, b sono primi fra loro Formula delle terne pitagoriche primitive Utilizzando le seguenti formule si possono ottenere tutte le terne pitagoriche primitive: a = m2 - n2 , b = 2mn con m e n primi tra loro e uno pari e l’altro dispari , c = m2 + n2 Attività Verrà presentato al visitatore un modello di cioccolata del teorema di Pitagora costruito utilizzando la terna pitagorica più piccola: 3-4-5 9 16 25 32 + 42 = 52 Successivamente si illustrano le proprietà delle terne pitagoriche 4. La serie armonica: la torre sporgente. All’inizio del suo libro “L’ossessione dei numeri primi” il matematico John Derbyshire presenta il seguente problema [7]. Dato un mazzo di 52 carte di lunghezza L facciamo scorrere la carta in cima senza muovere le altre. Quanto 1 possiamo sporgerla prima che essa cada? Ovviamente fino a L 2 Ripetiamo ora l’operazione muovendo insieme la prima e la seconda carta. Quanto possiamo sporgerle prima che esse cadano? Il trucco è quello di pensare le due carte come una singola unità. Il baricentro si trova ora a 1 1 metà del complesso delle due carte e quindi queste possono sporgere di L 2 4 1 1 1 Si può provare che per le prime tre carte la sporgenza massima è L 2 4 6 1 1 1 1 1 1 .. E in generale per le prime n carte si arriva all’espressione L 2n 2 4 6 8 10 Quest’ultima può essere riscritta così: 1 1 1 1 1L 1 .. 2 3 4 5 n2 1 Il termine tra parentesi è la somma dei primi n della successione armonica n Per il teorema di divergenza della “serie armonica” si ha: 1 1 1 1 1 lim 1 .. 2 3 4 5 n n Ne segue che la sporgenza del mazzo può essere grande a piacere (a patto di avere un numero sufficiente di carte) Attività Si sfiderà il visitatore a realizzare una torre di tavolette di cioccolata (che prendono ora il posto delle carte da gioco) che sporga lateralmente il più possibile . Si terrà nota dei record ottenuti aggiornandoli, premiando gli autori delle performances. La torre potrà essere realizzata anche attraverso una simulazione al computer mediante un’apposita applicazione. Al termine si farà presente il ruolo che gioca la serie armonica nella sfida e di come, a patto di utilizzare numero adeguato di tavolette, non ci sia limite alla sporgenza della torre. un 5. Il teorema di Pick. Nel suo lavoro del 1899 Geometriches zur Zahlenlehre (La geometria per la teoria dei numeri) il matematico austriaco Georg Alexander Pick (1859, 1942) nel “ .. tentativo di porre le basi della teoria dei numeri in modo nuovo e, fin dal principio, su basi geometriche…” dimostra un elegante e sorprendente teorema [8]. Dato un poligono P con i vertici a coordinate intere, indicati con: I : il numero di punti a coordinate intere interni al poligono F: il numero di punti a coordinate intere appartenenti alla frontiera di P l’area di P vale: Area(P) I 1 1 2 Esempio: Attività Il visitatore sarà invitato a verificare la correttezza del teorema di Pick su porzioni di tavolette di cioccolata vera o modelli in plastica, e con apposite animazioni al computer. 6. Il problema della scacchiera mutilata. Il problema di matematica ricreativa soprannominato ‘il problema della scacchiera mutilata’ nasce dalla domanda: “se si eliminano le due caselle bianche poste ai vertici di una scacchiera 8×8 è possibile ricoprire esattamente senza sovrapposizioni la superficie restante con 31 tessere del domino di dimensioni 1 e 2 volte il lato di una casella?” La risposta è no e lo si può provare con il seguente ragionamento [9]. Si parte dalla considerazione ovvia che ogni tessera posta sulla scacchiera copre sempre una casella nera e una casella bianca; ne segue che dopo aver utilizzato le prime 30 tessere sono state coperte 30 caselle nere e 30 caselle bianche: restano scoperte due caselle entrambe di colore nero (e quindi non adiacenti) che l’ultima tesserina non potrà mai ricoprire! Il ragionamento può essere applicato anche a scacchiere di forma rettangolare. Attività Si chiederà al visitatore di ricoprire una superficie composta da quadretti di cioccolata bianca e nera, disposti a scacchiera, con stecche di cioccolata formata da due quadretti. L’animatore spiegherà successivamente in quali casi il ricoprimento è possibile e in quali questo è irrealizzabile. 7. Numeri figurati. Numeri triangolari Consideriamo le seguenti figure formate da punti disposti in una struttura triangolare: … Possiamo valutare la quantità dei punti contandoli (i numeri ottenuti si dicono “numeri triangolari”), tuttavia tale metodo risulta poco efficiente quando i punti sono numerosi. Cerchiamo allora un metodo alternativo ad esempio mediante l’uso di una formula. A tale scopo vediamo cosa succede quando si sommano due triangoli uguali: come si vede si ottiene una struttura rettangolare nel quale il numero delle colonne e delle righe differiscono per una unità. Cioè: Tn + Tn = Rn,n+1 (dove Tn indica un numero triangolare che ha sull’ultima riga n oggetti e Rn,n+1 un figura rettangolare di oggetti con n righe e n+1 colonne) Il numero di punti del rettangolo si ottiene moltiplicando tra loro il numero di righe e quello delle colonne, quindi: Tn + Tn = Rn,n+1 = n(n+1) ma allora: Tn + Tn = n(n + 1) da cui: Tn = n(n 1) 2 Numeri quadrati Nella figura è rappresentato il numero quadrato 36. Si vede chiaramente che il quadrato può essere scomposto in figure come quelle che seguono (chiamate “gnomoni”): e siccome il numero di punti di tali figure non sono altro che i numeri dispari, si ottiene l’interessante proprietà: 1 + 3 + 5 + 7 + 9 + 11 = 36 Si può in effetti affermare che ogni numero quadrato è la somma dei primi numeri dispari. Attività Si guiderà il visitatore alla scoperta della formula per calcolare la quantità di oggetti disposti all’interno di figure triangolari Successivamente si mostrerà attraverso opportune configurazioni di oggetti (gli gnomoni) che la somma dei primi numeri dispari dà come risultato sempre un quadrato Risorse Il Chomp e la teoria dei giochi. Martin Gardner, Mathematical Games. Scientific American, Jan. 1973, pp.110-111. Emanuele Delucchi, Giovanni Gaiffi, Ludovico Pernazza, Giochi e percorsi matematici, Springer http://crf.uniroma2.it/wp-content/uploads/2010/04/Spunti-e-ricerche-intorno-al-gioco-del-chomp.pdf Il paradosso dell'area scomparsa: come creare cioccolata dal nulla. http://www.marianotomatis.it/blog.php?post=blog/20110728 Terne pitagoriche. http://utenti.quipo.it/base5/pitagora/ternepit.htm La serie armonica: la torre sporgente. John Derbyshire, L'ossessione dei numeri primi, Bollati Boringhieri Il teorema di Pick. http://crf.uniroma2.it/wp-content/uploads/2010/04/Geometria-e-teoria-dei-numeri-aggiornato.pdf Il problema della scacchiera mutilata. http://crf.uniroma2.it/wp-content/uploads/2010/04/Geometria-e-teoria-dei-numeri-aggiornato.pdf I numeri figurati php.math.unifi.it/convegnostoria/materiali/GiacardiNumeriFigurati.pdf http://areeweb.polito.it/didattica/polymath/htmlS/argoment/ParoleMate/Mag_09/ Aritmogeometria.htm Pannelli IL CHOMP Il Chomp è la sfida tra due contendenti che devono, ad ogni mossa, mangiare almeno un quadratino di cioccolato. Chi mangia il quadratino avvelenato in basso a sinistra perde; vince quindi chi obbliga l’avversario a mangiare il veleno. La regola è che i giocatori hanno una bocca rettangolare: volendo mangiare un certo quadratino, il giocatore mangerà anche tutti quelli che si trovano più a destra e più in alto di esso. 16 9 25 IL TEOREMA DI PITAGORA 32 + 42 = 52 https://www.liceo-orazio.gov.it http://www.eurochocolate.com http://crf.uniroma2.it/ CREARE CIOCCOLATO DAL NULLA E’ veramente possibile? Chiedilo alla matematica! LA FORMULA DI PICK Area = I P/2 1 https://www.liceo-orazio.gov.it http://www.eurochocolate.com http://crf.uniroma2.it/ BIMINI E’ possibile ricoprire tutti i quadretti con bimini di cioccolata? LA TORRE SPORGENTE Cadrà? Dalla matematica una risposta sorprendente! https://www.liceo-orazio.gov.it http://www.eurochocolate.com http://crf.uniroma2.it/ TRIANGOLI DI CIOCCOLATINI QUADRATI DI CIOCCOLATINI https://www.liceo-orazio.gov.it http://www.eurochocolate.com http://crf.uniroma2.it/