Il teorema di Pitagora conta oramai centinaia di dimostrazioni adatte alle più disparate
situazioni didattiche; recentemente è emerso che una delle dimostrazioni più apprezzate
da insegnanti e studenti è quella ad opera di Henry Perigal (1801-1898), un modesto
agente di cambio inglese con la passione per la matematica. Di famiglia povera, egli fu
molto orgoglioso del suo contributo allo scibile matematico, tanto da disporre che sulla sua
tomba venisse inciso un diagramma recante la sua dimostrazione (vedi figura).
E' grazie a Geogebra se oggi la dimostrazione di Perigal acquista una marcia in più
nell'efficacia didattica. Ne è la prova questa elegante versione animata, alla portata di
allievi di ogni grado e ordine scolastici.
http://www.geogebra.org/en/upload/files/italian/giovanna/Pitagora_Perigal.html
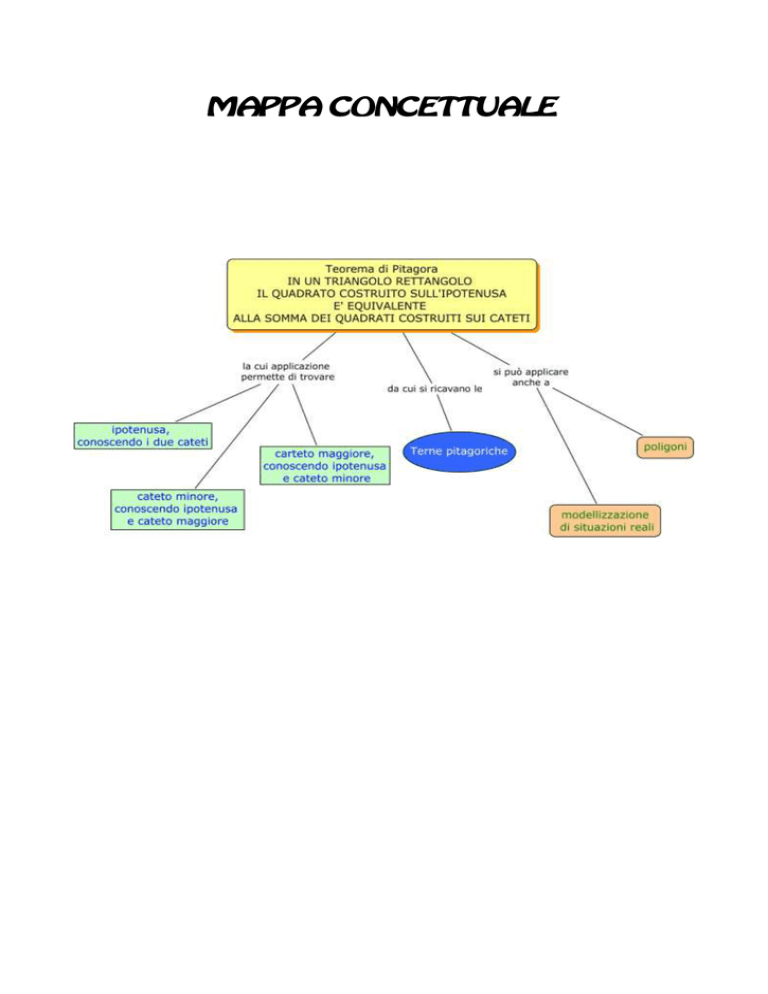
Con Geogebra è possibile realizzare semplicemente una costruzione come
la seguente e verificare la validità del Teorema di Pitagora
Chiamati i=ipotenusa, C=cateto maggiore e c=cateto minore, si ottengono le
seguenti relazioni:
1) i2=C2+c2 da cui estraendo la radice quadrata di entrambi i membri si ottiene:
i=√
2) C =i -c da cui estraendo la radice quadrata di entrambi i membri si ottiene:
2
2
2
C=√
3) c =i -C da cui estraendo la radice quadrata di entrambi i membri si ottiene:
2
2
2
c=√
LE TERNE PITAGORICHE
Gli antichi popoli Egiziani e Babilonesi conoscevano la relazione tra i lati di un
triangolo rettangolo espressa dal Teorema di Pitagora molto prima che il
matematico dimostrasse il teorema.
Sulle rive del Nilo, gli Egiziani utilizzavano una tecnica molto particolare per
delimitare gli appezzamenti dei terreni agricoli. Essi infatti avevano la necessità di
costruire degli angoli retti con pochi strumenti rudimentali. La tecnica consisteva nel
prendere una fune di una certa lunghezza, sulla quale si facevano tredici nodi a
intervalli regolari; poi si fissava a terra la fune con dei pioli infilando il primo piolo
nel punto d’incontro tra il primo e l’ultimo nodo; quindi fissavano i pioli 2 e 3
rispettivamente nel quarto e nell’ottavo nodo e, se la corda era ben tesa, in
corrispondenza del secondo piolo si otteneva un angolo retto.
Questi popoli antichi conoscevano delle terne di numeri che, pur non sapendo
perché, davano origine a dei triangoli rettangoli:
3, 4, 5
5, 12, 13
7, 24, 25
8, 15, 17
10, 24, 26
Una TERNA PITAGORICA è un insieme di tre numeri naturali corrispondenti alle
misure dei lati di un triangolo rettangolo e quindi legati tra loro dalla relazione
espressa dal Teorema di Pitagora.
Una terna pitagorica si dice primitiva quando è formata da numeri primi tra loro.
ES.
3, 4, 5 oppure 8, 15, 17
Una terna pitagorica si dice derivata quando si ottiene moltiplicando la terna
primitiva per uno stesso fattore diverso da zero.
ES. 12, 16, 20 (si ottiene da 3, 4, 5 moltiplicando per 4)
Pitagora riuscì a determinare una procedura per generare le terne pitagoriche a
partire da un numero n naturale:
c=d (n° dispari)
C=
i=
c=2p (n° pari)
C=p2-1
i= p2+1