Il teorema di Pitagora e le terne pitagoriche
a cura di Flavio Cimolin
(ultimo aggiornamento: 03/02/2003)
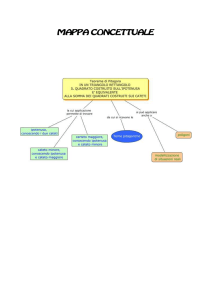
Ovvero... in un triangolo rettangolo la somma dei quadrati costruiti sui cateti è uguale al quadrato
costruito sull'ipotenusa.
E’ davvero superfluo spendere altre parole per questa formula basilare della geometria euclidea, che
recitano senza neanche pensarci anche gli studenti più pigri fin dalle scuole inferiori. Eppure nella
sua semplicità essa funge da base per innumerevoli applicazioni matematiche di ogni tipo (basti
pensare alla misura delle distanze nel piano cartesiano nonché in tutti i sistemi a più dimensioni, al
teorema fondamentale della trigonometria o al calcolo di numeri complessi).
Particolarmente interessante è un'altra formula strettamente legata a questa, tratta il problema delle
terne pitagoriche. Una terna pitagorica (a,b,c) è una tripletta di numeri interi che soddisfano
l'uguaglianza del teorema di Pitagora (ovvero per i quali esiste un triangolo rettangolo di lati interi
a,b,c). Il primo esempio è costituito da a=3, b=4, c=5, infatti 32 + 42 = 52.
Ebbene, si può dimostrare che tutte le terne pitagoriche possono essere generate dalle seguenti
formule:
2
2
• a=u -v
• b=2*u*v
2
2
• c=u +v
Dove u e v sono numeri naturali primi fra loro e non entrambi dispari.
La storia ha poi fatto sì che questo teorema conducesse ad una congettura molto forte, ovvero che
non esistono "terne pitagoriche" con l'esponente maggiore di 2. Questo problema va sotto il nome di
Ultimo Teorema di Fermat, e nonostante la sua semplicità, è stato dimostrato solo nel 1994.
http://www.matematicamente.it