Ponti di misura - 1
Ponti di misura
1 - Il ponte di Wheatstone
Schema generale
Il ponte di Wheatstone trova numerose applicazioni nel campo delle misure elettriche per la
determinazione di parametri resistivi.
Il suo impiego è particolarmente diffuso nel campo dei trasduttori che associano a una
variazione della grandezza fisica di interesse una variazione di resistenza.
Nel suo schema essenziale un ponte di Wheatstone è costituito da quattro resistenze collegate
come in Fig.1.1A, alimentate da un generatore di tensione costante E.
Fig.1.1 - Ponte di Wheatstone (A) e circuito equivalente di Thevenin (B).
Il ponte è detto in equilibrio quando la tensione a vuoto fra i punti A e B è nulla:
VAB = 0
⇒
⎧ I ' ' R1 = I ' R3
⎨
⎩ I ' ' R2 = I ' R4
⇒
R1 R3
=
=k
R2 R4
(1.1)
La condizione di equilibrio viene segnalata dal rivelatore di zero (null detector), tipicamente
un voltmetro ad alta sensibilità.
In tali condizioni, il ponte consente di determinare il valore di una delle quattro resistenze (ad
esempio R2), quando siano noti i valori delle altre tre.
In pratica si procede fissando, ad esempio, le resistenze R3 ed R4, in modo da ottenere un
idoneo rapporto k, quindi si varia la resistenza R1 finchè il ponte raggiunge l’equilibrio.
In tal modo il valore della resistenza incognita risulta R2 =R1/k.
In queste applicazioni, la resistenza R1 è variata con opportuni sistemi (resistori a decadi:
1000Ω, 100Ω, 10Ω, 1Ω, 0.1Ω, 0.01Ω ecc.) con i quali è possibile inserire resistenze note a
priori con elevata accuratezza.
L’impiego del ponte in condizioni di equilibrio è usuale nei sistemi da laboratorio o nelle
apparecchiature che realizzano il controllo automatico a microprocessore della procedura di
azzeramento.
© 2005, Nicola Locci
Complementi di Misure
Ponti di misura - 2
Il ponte sbilanciato
Negli impieghi con trasduttori, il ponte non viene utilizzato in condizioni di perfetto
equilibrio, bensì nell’intorno delle condizioni di equilibrio.
Si supponga pertanto che, rispetto alle condizioni di equilibrio la resistenza R2 nella Fig.1.1
subisca una piccola variazione δR, portandosi al valore:
R2′ = R2 + δR = R2 (1 + x)
posto
x=
δR
R2
(1.2)
Per il ponte di misura in tali condizioni risulta utile la rappresentazione con il circuito
equivalente secondo Thevenin, riportata in Fig.1.1B.
La tensione e la resistenza del generatore equivalente secondo Thevenin, visti dai punti A e B,
sono dati rispettivamente da:
V AB0 = V AD0 − VBD0 =
E
E
R2′ −
R4
R3 + R4
R1 + R2′
R0 = R1 R2′ + R3 R4
(1.3)
Per la valutazione della resistenza equivalente R0 è stata trascurata, per semplicità, la
resistenza interna della batteria.
Considerare il ponte nell’intorno dell’equilibrio significa ammettere che le variazioni di x
siano molto piccole (x<<1). La tensione a vuoto V AB0 può pertanto esprimersi nella forma:
E
E
R2 (1 + x) −
R4
R1 + R2 (1 + x)
R3 + R4
kx
kx
=E
≅E
[k + (1 + x)] (k + 1) (k + 1) 2
V AB0 =
(1.4)
Nell’espressione precedente si nota che, se le variazioni di x sono molto piccole (x<<1),
allora la tensione a vuoto V AB0 può approssimarsi con una funzione lineare in x.
Sensibilità del ponte
Definiamo la sensibilità del ponte intorno all’equilibrio come il rapporto fra la tensione in
uscita V AB0 e la corrispondente variazione del parametro x di interesse:
S=
V AB0
x
=E
k
k
≅E
[k + (1 + x)] (k + 1) (k + 1) 2
se ( x << 1)
(1.5)
Appare interessante determinare quando la sensibilità del ponte è massima, per un
funzionamento intorno all’equilibrio.
A tale scopo è sufficiente annullare la derivata della sensibilità S rispetto al parametro k.
Se trascuriamo x rispetto all’unità, si ottiene:
∂S
= 0 ⇒ k = 1 ⇒ R1 = R2
∂k
; R3 = R4
(1.6)
In tale ipotesi la tensione a vuoto del ponte è:
VAB0 ≅
E
E δR
x=
4
4 R2
(1.7)
e si ha la massima sensibilità.
© 2005, Nicola Locci
Complementi di Misure
Ponti di misura - 3
L’approssimazione introdotta nell’espressione della tensione di sbilanciamento è valida se,
come accade nella pratica, le variazioni δR risultano molto minori di R2 (x<<1). È opportuno
osservare che solo in tali ipotesi l’uscita del ponte può ritenersi lineare con δR.
Infine, per misurare la tensione VAB a vuoto, cioè senza che vi sia un effetto di carico
introdotto sul sistema dal voltmetro, è necessario l’impiego di un dispositivo di misura con
elevato valore dell’impedenza d’ingresso, tipicamente un amplificatore per strumentazione.
La condizione di massima sensibilità del ponte può essere ottenuta facendo le resistenze tutte
uguali, R1 = R2 = R3 = R4, con valore R pari a quello dell’elemento sensibile a riposo.
Compensazione delle connessioni
In certi casi, come quelli in cui il ponte viene utilizzato in un sistema di trasduzione con
variazioni resistive e qualora l’elemento sensibile risulti lontano dal ponte di misura, bisogna
considerare anche la resistenza Rc dei cavetti di collegamento (vedi Fig.1.2A).
Fig.1.2 - Compensazione dei collegamenti al ponte.
Per la corretta compensazione del ponte in condizioni di equilibrio (δR=0), il lato CA dello
schema di Fig.1.2A dovrebbe contenere una resistenza di valore R’=R+2Rc
Un affinamento dello schema di Fig.1.2A, che evita la necessità di determinare la resistenza
dei cavetti per poterne tener conto, può essere realizzato con la connessione a tre cavetti
(metodo Siemens, rappresentato in Fig.1.2B).
Con tale connessione si compensano, oltre alle resistenze proprie dei cavetti anche le loro
eventuali variazioni termiche, mentre il terzo cavetto che porta al voltmetro è ininfluente,
risultando una sonda praticamente non percorsa da corrente.
2 - Il rivelatore di sbilanciamento
Misura della tensione di sbilanciamento
Si consideri un ponte sbilanciato e supponiamo di prelevare la tensione fra i punti A e B,
dovuta alla variazione di resistenza δR, tramite un amplificatore per strumentazione (Fig.2.1).
Nei casi pratici la tensione E di alimentazione del ponte è riferita alla massa comune e risulta
pertanto importante analizzare il comportamento dello stadio differenziale nei riguardi della
tensione di modo comune. A tale scopo, per ciascun punto A e B del ponte si possono
determinare i generatori equivalenti di Thevenin, riferiti alla massa comune.
© 2005, Nicola Locci
Complementi di Misure
Ponti di misura - 4
Fig.2.1 - Ponte sbilanciato con amplificatore per strumentazione.
Questi sono rappresentati dalle tensioni a vuoto VA0 e VB0 e dalle resistenze equivalenti RA0 e
RB0 (Fig.2.1). Dall’analisi del circuito risulta, ponendo x=δR/R:
1+ x
E
( R + δR) = E
2 R + δR
2+ x
E
E
R=
=
2R
2
V A0 =
VB 0
1+ x
R( R + δR)
=R
2 R + δR
2+ x
R
=
2
R A0 =
RB 0
(2.1)
Si nota che, per piccoli valori di x (x<<1), la tensione di modo comune VC e la tensione
differenziale VD si possono approssimare rispettivamente a:
E
1
VC = (V A0 + VB 0 ) ≅
2
2
VD = (V A0 − VB 0 ) ≅
Ex
4
(2.2)
Le resistenze sugli ingressi dello stadio differenziale sono date rispettivamente dalle
resistenze RA0 ed RB0 e queste, in prima approssimazione, valgono entrambe R/2 (per x<<1).
Per la misura della tensione a vuoto fra i punti A e B del ponte sbilanciato, si preferisce un
amplificatore per strumentazione, in quanto presenta una reiezione del modo comune
normalmente migliore rispetto alle configurazioni semplicemente differenziali.
Un circuito per linearizzare il ponte
Si è detto che il ponte sbilanciato presenta una tensione d’uscita che non risulta lineare con la
variazione parametrica x, a meno che questa non risulti sufficientemente piccola.
Quando si è interessati a una linearizzazione dell’uscita del ponte di misura, si può ricorrere a
circuiti appositi, come quello rappresentato in Fig.2.3.
Fig.2.3 - Un circuito per linearizzare il ponte.
Indichiamo al solito x=δR/R. Considerando ideale il comportamento degli amplificatori
© 2005, Nicola Locci
Complementi di Misure
Ponti di misura - 5
operazionali e per effetto della massa virtuale in ingresso a OP1 e OP2, risulta:
E
R
V1 = −i2 R (1 + x) = − E (1 + x)
VA = VB = 0
i3 =
i1 =
E
= i2
R
(2.3)
Dall’esame del circuito si ottiene inoltre:
i4 = −
V1 E
= (1 + x)
R R
(2.4)
E
E E
i5 = i4 − i3 = (1 + x) − = x
R
R R
La tensione V2 in uscita dall’amplificatore operazionale OP2 risulta infine:
V2 = Ri5 = Ex
(2.5)
che mostra come si sia ottenuta la desiderata linearizzazione dell’uscita del ponte.
3 - Un esempio di applicazione dei circuiti a ponte
Gli estensimetri
Gli estensimetri (strain gauges) sono trasduttori che si basano sull’effetto piezoresistivo, ossia
la proprietà dei materiali di variare la propria resistenza elettrica con la deformazione.
Gli estensimetri più comuni sono metallici, costituiti da un sottilissimo filo conduttore
(diametro dell’ordine dei 50 μm) disposto come nello schema di Fig.3.1A e tenuto in
posizione da un sottile strato di resina. Sono realizzati con leghe come, ad esempio,
manganina (84% Cu, 12% Mn, 4% Ni) o costantana (60% Cu, 40% Ni).
Con sufficiente approssimazione e trascurando fenomeni secondari, si può ritenere che la
variazione relativa di resistenza (δR/R) sia proporzionale alla deformazione (ε = δl/l = strain):
δR
δl
= KG = KG ε
R
l
(3.1)
Il coefficiente di proporzionalità KG è detto gauge factor.
Per gli estensimetri realizzati con metalli, il gauge factor KG è dell’ordine di 2.
Fig.3.1 - Estensimetri: A) Schema; B) Applicazione.
Gli strain gauges sono commercialmente disponibili con diversi valori di resistenza; i più
© 2005, Nicola Locci
Complementi di Misure
Ponti di misura - 6
comuni sono di 120 Ω, 350 Ω e 1000 Ω.
Spesso vengono impiegati anche materiali semiconduttori, caratterizzati da una maggiore
variazione relativa della resistenza con la deformazione.
Un’applicazione degli estensimetri
Un impiego classico degli estensimetri si ha nel rilievo sperimentale della deformazione di
una struttura elastica, tipicamente metallica. Facendo riferimento alla Fig.3.1B, l’estensimetro
viene incollato con resine epossidiche sulla struttura soggetta a deformazione.
Nell’esempio in figura si tratta di un provino cilindrico, per esempio d’acciaio, di sezione A e
lunghezza utile L, sottoposto a uno forza F di trazione assiale. In conseguenza della
sollecitazione di trazione, il provino risulta sede di uno sforzo σ (forza per unità di area) e
subisce una deformazione ε corrispondente all’allungamento relativo δL/L. Naturalmente, la
deformazione δL/L dell’asta è uguale a quella δl/l dell’estensimetro ad esso solidale (si tratta
infatti di variazioni relative).
Pertanto, la sollecitazione di sforzo σ e la deformazione ε risultano rispettivamente:
σ=
F
A
ε=
δL δl
1 δR
= =
L
l KG R
(3.2)
Così, da una misura di variazione della resistenza δR è possibile risalire alla misura della
deformazione ε.
Queste considerazioni trovano un’interessante applicazione pratica nella determinazione del
diagramma sforzo-deformazione (σ-ε) che caratterizza la resistenza dei materiali (almeno
nella parte lineare). Lo sforzo σ si può determinare conoscendo la sezione A e misurando la
forza applicata F. La deformazione ε si misura da una variazione di resistenza δR.
Un andamento tipico del diagramma sforzo-deformazione per gli acciai è riportato in Fig.3.2B.
Il primo tratto di tale diagramma (σ-ε) rappresenta il campo di comportamento elastico,
caratterizzato dalla proporzionalità tra sforzi e deformazioni per mezzo del modulo di elasticità
EM caratteristico di ciascun materiale: σ = EM ε (legge di Hooke).
L’applicazione di uno sforzo in tale campo non lascia deformazioni permanenti nel materiale,
quando lo sforzo viene riportato a zero. Viceversa si hanno deformazioni residue permanenti
quando viene superato del limite di snervamento σsn e si riporta a zero lo sforzo.
Fig.3.2 - Estensimetri: A) Applicazione; B) Diagramma (σ-ε).
Naturalmente, oltre la zona di snervamento, le deformazioni irreversibili subite sia dal
provino che dall’estensimetro rendono quest’ultimo non più utilizzabile. Alla fine, al crescere
dello sforzo applicato e delle conseguenti deformazioni, il provino giunge al punto di rottura.
© 2005, Nicola Locci
Complementi di Misure
Ponti di misura - 7
Celle di carico
Un’altra applicazione tipica degli estensimetri si ha nella misura di forze.
Infatti, montando un estensimetro su una struttura metallica di cui sia noto il modulo di
elasticità EM e che abbia delle dimensioni note e lavori rigorosamente in campo elastico, si
può determinare la forza applicata dalle variazioni di resistenza δR, essendo:
F = σ A = EM ε A =
E M A δR
⋅
KG R
(3.3)
Quindi anche una forza F può essere determinata con una misura di resistenza δR.
Tale principio porta alla realizzazione delle cosiddette celle di carico: apparecchiature assai
diffuse e impiegate nella costruzione delle bilance elettroniche per la misura di forze.
Osserviamo infine che, nell’impiego pratico degli estensimetri, particolare cura deve essere
posta nel garantire che la struttura sotto sforzo trasmetta realmente le proprie deformazioni
all’estensimetro: pertanto l’incollaggio dovrà essere a regola d’arte, stabile nel tempo e con la
temperatura, sufficientemente elastico.
Ponte linearizzato
Quando il comportamento del ponte sbilanciato risulta eccessivamente non lineare,
compromettendo la qualità della misura, si provvede con tecniche di linearizzazione.
Un caso interessante, che consente un ottimo comportamento lineare del sistema di misura, si
presenta nella costruzione delle celle di carico. In tali dispositivi si impiega spesso una
struttura elastica in acciaio inox (vedi la Fig.3.3), realizzata con un’asta incastrata e inflessa.
In tal modo il carico della forza F determina, nella sezione dell’asta, uno stato di sforzo
simmetrico rispetto all’asse neutro.
Allora risulta conveniente disporre sull’asta due estensimetri identici e sottoporli a
sollecitazioni uguali ed opposte, per esempio di trazione e di compressione, corrispondenti
rispettivamente a (R+δR) e (R-δR).
Tali estensimetri saranno quindi inseriti su due lati adiacenti del ponte di misura (Fig.3.3A).
Fig.3.3 - Schemi con montaggio simmetrico, per linearizzare il ponte.
Indicando con x=δR/R la variazione relativa di resistenza, si verifica facilmente, con
riferimento alla Fig.3.3A, che la tensione a vuoto in uscita dal ponte risulta:
V AB0 = V AD0 − VBD0 =
E
E
E
R (1 + x) −
R= x
2R
2
R (1 + x) + R(1 − x)
(3.4)
Pertanto, oltre a realizzare la linearità fra tensione d’uscita e variazione di resistenza, si
© 2005, Nicola Locci
Complementi di Misure
Ponti di misura - 8
raddoppia anche la sensibilità del dispositivo.
Con riferimento invece alla disposizione full-bridge, rappresentata in Fig.3.3B, si raggiunge
una situazione ancora migliore, in quanto, mantenendo la linearità, si raddoppia ulteriormente
la sensibilità. Infatti:
V AB0 = V AD0 − VBD0 =
E
[ R (1 + x ) − R (1 − x )] = Ex
2R
(3.5)
Entrambe le soluzioni rappresentate in Fig.3.3 hanno inoltre il pregio di essere insensibili alle
variazioni di temperatura, se queste interessano in uguale misura tutti gli estensimetri.
Esempio
Supponiamo una struttura elastica sulla quale è incollato un estensimetro, che abbia una
deformazione ε = δL/L = 10-3.
Supponiamo inoltre che l’estensimetro abbia resistenza di 350 Ω e gauge factor KG pari a 2.
La variazione di resistenza dovuta alla deformazione risulta:
δR = R⋅ε⋅KG = 350Ω⋅10-3⋅2 = 0,7Ω; corrispondente a x = δR/R = 0,002 = 0,2%.
Per misurare tali variazioni si impieghi una struttura a ponte sbilanciato full-bridge costituita.
Se il ponte è alimentato con la tensione E = 10 V, allora la tensione a vuoto in uscita dalla
migliore configurazione del ponte (la più sensibile) è pari a: V AB0 = Ex = 10 ⋅ 0,002 = 20 mV .
4 - Considerazioni sull’approssimazione di linearità
Riprendiamo brevemente l’approssimazione di linearità, che viene spesso adottata per motivi
di semplicità. Questa approssimazione risulta tanto meno accettabile quanto più ci si allontana
dalla condizione di equilibrio e quindi al crescere della variazione parametrica x = δR/R.
Abbiamo già stabilito che le espressioni esatta e approssimata per la tensione Vm misurata in
uscita dal ponte sono:
R⎤
R ⋅ δR
⎡ R + δR
=E
=
Vm = V AD − VBD = E ⎢
−
⎥
2 R ⋅ (2 R + δR )
⎣ 2 R + δR 2 R ⎦
E
δR / R
E x
= ⋅
= ⋅
2 (2 + δR / R ) 2 2 + x
Vm ≅
E δR E
= x
4 R
4
(4.1)
(4.2)
avendo indicando con E è la tensione di alimentazione, e supponendo che tutte le resistenze
siano uguali e di valore R.
Di fatto, si misura sempre la tensione effettiva Vm e da questa dobbiamo risalire alla
variazione parametrica x = δR/R e poi alla grandezza di interesse.
Esaminiamo cosa comporta usare la relazione esatta oppure quella approssimata.
Esempio con un sensore di temperatura
Nei sistemi di trasduzione, la variazione resistiva δR è conseguenza di una corrispondente
variazione di un’altra grandezza fisica che ci interessa misurare.
Consideriamo come esempio un sensore di temperatura molto diffuso: la sonda al Platino
© 2005, Nicola Locci
Complementi di Misure
Ponti di misura - 9
PT100 (della quale si parlerà più diffusamente in un altro capitolo).
In questo caso, la variazione di resistenza δR del sensore è proporzionale alla temperatura T
da misurare con una semplice relazione del tipo: δR = RαT. Dove:
• R è la resistenza alla temperatura di 0°C, pari appunto a R = 100 Ω,
• T è la temperatura in °C,
• α è il coefficiente di variazione della resistenza del sensore che vale α = 0,004 Ω/(Ω⋅°C).
L’espressione esatta della variazione parametrica si ottiene dalla 4.1:
x (1 −
2Vm
4V
4Vm
)= m; x=
E
E
E − 2Vm
⇒ δR = R ⋅
4Vm
E − 2Vm
(4.3)
L’ espressione approssimata per la variazione parametrica si ottiene dalla 4.2:
x stima =
4Vm
E
⇒ δRstima = R ⋅
4Vm
E
(4.4)
Per quanto riguarda la temperatura, le espressioni esatta e approssimata sono:
T (°C) =
1 δR 1
1
4Vm
1
4Vm
= x= ⋅
=
⋅
α R α
α E − 2Vm 0,004 E − 2Vm
1 δRstima 1
1 4V
1
4V
= x stima = ⋅ m =
⋅ m
Tstima (°C) =
α R
α
α E
0,004 E
(4.5)
I valori numerici
Per valutare l’errore che si commette nell’impiego della relazione approssimata, consideriamo
un’applicazione in cui il range di temperatura sia fra –100 °C e +200 °C.
La condizione di equilibrio sia per T = 0 °C e la tensione di alimentazione sia E = 2 V.
Riportiamo i valori di interesse nella tabella seguente.
In particolare, la tensione Vm esposta nella tabella è quella realmente misurata con un
voltmetro (oppure determinata con l’espressione esatta).
T
x = δR/R = αT
Vm
(°C)
(-)
(mV)
-100
-0,40
-250,0
0
0
0
+100 +200
+0,40 +0,80
+166,7 +285,7
Tstima
(°C)
ΔT = (Tstima – T) (°C)
ΔT/T
(%)
-125,0
-25,0
-25,0
0
0
0
+83,3 +142,9
-16,7 -57,2
-16,7 -28,6
Si nota che l’errore relativo ΔT/T per la temperatura Tstima risulta molto elevato, soprattutto
agli estremi del range.
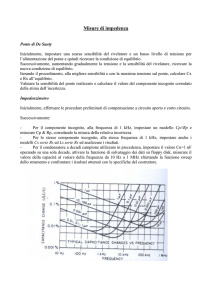
Nel grafico di Fig.4.1 si riporta, in funzione della variazione x = δR/R, l’andamento della
tensione Vm realmente misurabile (linea nera) e la sua approssimazione lineare (linea rossa).
A commento del grafico e della tabella, osserviamo che, alla temperatura effettiva di +100 °C,
si avrebbe una variazione parametrica x di +0,4 e il voltmetro segnerebbe +166,7 mV.
Deducendo la stima della temperatura da questa lettura di tensione, e impiegando la relazione
approssimata, si avrebbe una Tstima = +83,3 °C. Si commette un errore del 16,7% in difetto.
© 2005, Nicola Locci
Complementi di Misure
Tensione (mV)
Ponti di misura - 10
500
400
300
200
100
0
-100
-200
-300
-0,40
-0,20
0,00
0,20
0,40
0,60
0,80
x=δR/R
Fig.4.1 - Legame fra tensione misurata Vm e variazione parametrica x = δR/R.
© 2005, Nicola Locci
Complementi di Misure