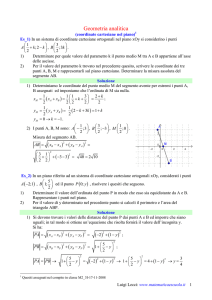
Esame di Circuiti Elettronici Analogici - 22 Marzo 2003
Vi
D1
R1
Vu
C
R2
Vi
D2
Vm
t
1. In condizioni stazionarie, per t < 0, essendo VI = 0, non ci sono generatori indipendenti di corrente
e di tensione quindi all’interno del circuito non circola corrente e le tensioni sono nulle. VU 0 = 0 ed
entrambi i diodi sono interdetti.
(a) Per t > 0 il diodo D1 si accende ed inizia a fluire corrente nel circuito. Tale corrente andrá a
caricare la capacitá C mentre il diodo D2 resta interdetto. L’equazione che regola il transitorio
U
é la seguente: VXR−V
= VRU2 + C dVdtU dove VX = VM − Vγ . Il transitorio si esaurisce quando
1
VU raggiunge un valore sufficiente ad accendere D2 ovvero quando VU = Vγ . La soluzione
−t
−t
γ
(1 − e τ ) = VM 2−Vγ (1 − e τ ) dove τ = RC
= RC
. La
dell’equazione risulta VU (t) = VMR−V
R2
2
2
R1 +R2
γ
, t = 4.92ns.
durata del transitorio si puó esprimere come t = −τ log VVMM−3V
−Vγ
R1 +R2
(b) Scrivere la netlist SPICE che consente di rispondere al quesito precedente.
VCC
RC
Vi
Q1
R
Vu
Q2
Q4
Q3
C
RE
VEE
2. Con riferimento al circuito in figura:
(a) Supponiamo che tutti i transistori lavorino in RND. In condizioni stazionarie e con Vu0 = 0V
β +1
u0
risulta: IC2 = VCCR−V
= 2.5mA, IE2 = F IC2 = 2.525mA, IB2 = IC2 = 25µA. Per il calcolo di
C
βF
βF
VEE +Vbe4
2
Ic4 occorre iterare la seguente equazione: −
= Ic4 (1 + ) con Vbe4 = VT log IIc4
. Si ricava
R
S
βF
che Ic4 = 2.44mA = Ic3 . Risulta che Ic3 + Ib2 = Ie1 , quindi Ie1 = 2.465mA. Vbe2 = VT log IIc2
=
S
714mV , mentre Ve2 = VEE + RE Ie2 = −2.475V . Quindi Vb2 = Ve2 + Vbe2 = −1.761V . Vbe1 =
β
VT log IIc1
con Ic1 = F Ie1 = 2.44mA da cui Vbe1 = 713mV . Infine Vi0 = Vb2 + Vbe1 = −1.048V .
S
βF +1
Verifica delle ipotesi. I = 2.44mA e V = V log Ic3 = 713mV . V = V + V = −4.287V ,
c3
be3
T
IS
b3
EE
be3
Vc3 = Vb2 = −1.761V , quindi Vbc3 = −2.526V < 0, Q3 in RND. Vb1 = Vi0 = −1.048V , Vc1 = VCC =
5V , quindi Vbc1 = −6.048V < 0, Q1 in RND. Vbc2 = Vb2 = −1.761V < 0, Q2 in RND.
βV
βV
(b) Si faccia riferimento al circuito in figura dove: rbe1 = I0 T = 1.02KΩ e rbe2 = I0 T = 1.00KΩ.
c1
c2
Lo specchio di corrente formato da Q4 e Q3 , poiché VA = ∞, presenta una resistenza di uscita
infinita e pertanto non influisce ai fini del calcolo della funzione di rete richiesta. Il transistore
Q1 é connesso a Collettore Comune mentre Q2 é connesso ad Emettitore Comune con resistenza
u (s) vb2 (s)
u (s)
= vvb2
dove vvb2
(s) vi (s)
(s)
βR
rappresenta il guadagno di tensione dell’emettitore comune Q2 e vale Av2 (s) = − r0IN 2C ,
con r
= r + (β + 1)R resistenza di ingresso di Q . vb2 (s) rappresenta il guadagno
di degenerazione sull’emettitore pari a RE . Av (s) =
IN 2
be2
0
vu (s)
vi (s)
E
2 vi (s)
(β0 +1)ZE
di tensione del collettore comune Q1 e vale Av1 (s) =
impedenza di carico di Q1 . Componendo si trova:
(c) Zi (s) = rbe1 + (β0 + 1)ZE = rbe1 + (β0 + 1)
IN 2
con ZE = sCrrIN
2 +1
β0 (β0 +1)RC
−
.
(1+sCrIN 2 )rbe1 +(β0 +1)rIN 2
rbe2 +(β0 +1)RE
.
1+sC[rbe2+(β0 +1)RE ]
R1
R2
Rx
−
V1
(β0 +1)ZE +rbe1
(s)
Av (s) = vvui (s)
=
+
R1
1
−
VU1
V2
+
VU
2
3. Con riferimento al circuito in figura:
(a) Punto di riposo. Si osserva che l’OPAMP1 + (Rx + R1 ) costituisce un amplificatore non
invertente pertanto V10 = 0 → VU 10 = 0. Si osserva che l’OPAMP2 + (R1 + R2 ) costituisce
un amplificatore non invertente poiché VU 10 = 0 pertanto V20 = 0 → VU 0 = 0.
(b) Poiché entrambi gli operazionali lavorano nella regione ad alto guadagno:
R2
R1
R1
2
2
2
), vu = v2 (1 + R
)− R
v = v2 (1 + R
) − v1 R
(1 + R
).
vu1 = v1 (1 + R
R1
R1 u1
R1
x
x
1
R2
R1
R2
vu = A1 v1 + A2 v2 dove A1 = − R1 (1 + Rx ) e A2 = 1 + R1 . Ac = 0 → A1 = −A2 .
Quindi Rx = R2 .
1
(c) Guadagno differenziale. vu1 = v1 (1 + R
). Per l’OPAMP2 risulta (v2 − v− )Ad2 = vu e
R2
vu −v−
v− −vu1
1
2
1
= R1 . Componendo risulta vu = R2R+R
v− − vu1 R
→ v− = v1 + R1R+R
vu .
R2
R1
1
2
R
Sostituendo: v2 − v1 −
Infine poiché Ad2 (s) =
R1
v
R1 +R2 u
Ad0
1+ ωs
0
=
vu
Ad2
da cui si ricava che
risulta Ad (s) = −
vu
v2 −v1
Ad0
R1
+1+ ωs
+R
1
2
0
Ad0 R
.
=
Ad2 (1+ R2 )
1
R
Ad2 +(1+ R2 )
1
.