vol1_blu_rec_16 1..8

Scheda
16
A Ripasso
Scheda per il recupero 16
Congruenza nei triangoli
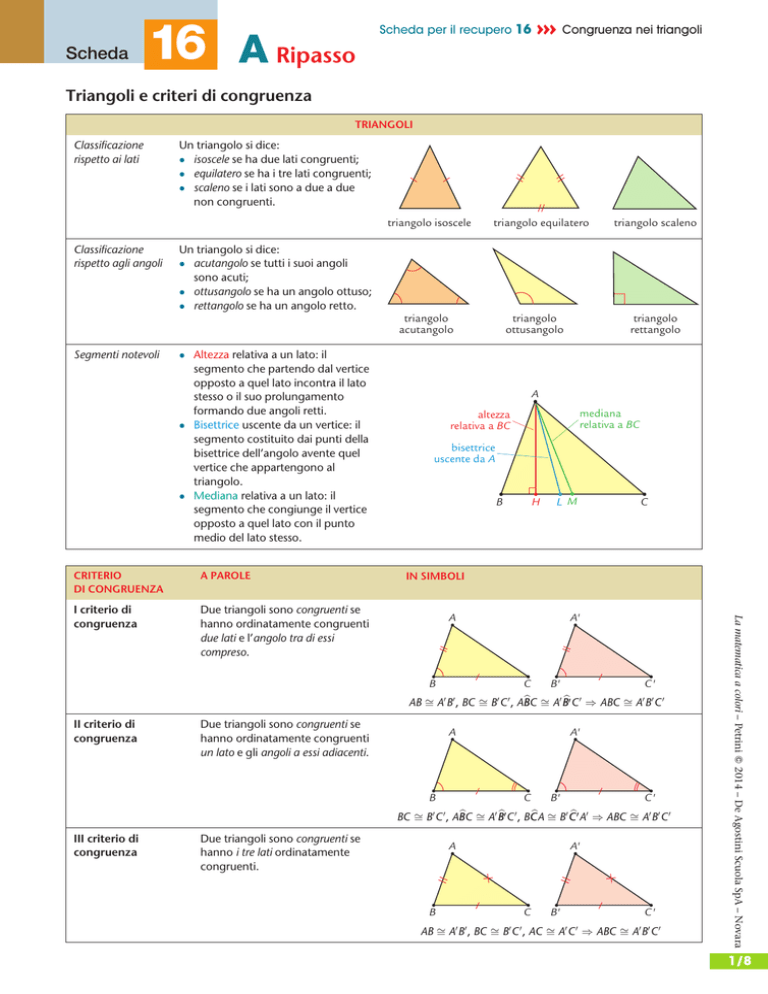
Triangoli e criteri di congruenza
TRIANGOLI
Classificazione
rispetto ai lati
Un triangolo si dice:
isoscele se ha due lati congruenti;
equilatero se ha i tre lati congruenti;
scaleno se i lati sono a due a due
non congruenti.
triangolo isoscele
Classificazione
rispetto agli angoli
triangolo equilatero
Un triangolo si dice:
acutangolo se tutti i suoi angoli
sono acuti;
ottusangolo se ha un angolo ottuso;
rettangolo se ha un angolo retto.
triangolo
ottusangolo
triangolo
acutangolo
Segmenti notevoli
triangolo scaleno
Altezza relativa a un lato: il
segmento che partendo dal vertice
opposto a quel lato incontra il lato
stesso o il suo prolungamento
formando due angoli retti.
Bisettrice uscente da un vertice: il
segmento costituito dai punti della
bisettrice dell’angolo avente quel
vertice che appartengono al
triangolo.
Mediana relativa a un lato: il
segmento che congiunge il vertice
opposto a quel lato con il punto
medio del lato stesso.
A PAROLE
I criterio di
congruenza
Due triangoli sono congruenti se
hanno ordinatamente congruenti
due lati e l’angolo tra di essi
compreso.
A
mediana
relativa a BC
altezza
relativa a BC
bisettrice
uscente da A
H
B
L M
C
IN SIMBOLI
A
A'
B
C
B'
C'
0
0
0
0
AB ffi A B , BC ffi B C , ABbC ffi A Bb C ) ABC ffi A B0 C 0
0 0
II criterio di
congruenza
Due triangoli sono congruenti se
hanno ordinatamente congruenti
un lato e gli angoli a essi adiacenti.
0
0
A
A'
B
C
B'
C'
BC ffi B 0 C 0 , ABbC ffi A0 Bb0 C 0 , BCbA ffi B 0 Cb0 A0 ) ABC ffi A0 B0 C 0
III criterio di
congruenza
Due triangoli sono congruenti se
hanno i tre lati ordinatamente
congruenti.
A
A'
B
C
0 0
0
0
B'
C'
0
0
0 0
AB ffi A B , BC ffi B C , AC ffi A C ) ABC ffi A B C 0
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
CRITERIO
DI CONGRUENZA
triangolo
rettangolo
1/8
Scheda
16
A Ripasso
Scheda per il recupero 16
Congruenza nei triangoli
Attenzione!
Negli enunciati dei tre criteri di congruenza è essenziale l’avverbio ordinatamente. Esso indica che i lati congruenti devono
essere opposti ad angoli congruenti e gli angoli congruenti a lati congruenti.
Proprietà dei triangoli isosceli
TEOREMI A PAROLE
TEOREMI IN SIMBOLI
A
In un triangolo isoscele (cioè avente due lati congruenti), gli
angoli adiacenti alla base sono congruenti.
AB ≅ AC ⇒ α ≅ β
β
α
B
C
A
Se in un triangolo due angoli sono congruenti, allora il
triangolo è isoscele e ha come base il lato adiacente agli
angoli congruenti.
α ≅ β ⇒ AB ≅ AC
β
α
B
C
A
AH altezza
⇒
In un triangolo isoscele, l’altezza relativa alla base è anche
mediana e bisettrice.
B
H
C
BH ≅ HC
BAH ≅ CAH
Disuguaglianze tra gli elementi di un triangolo
A PAROLE
Teorema
dell’angolo
esterno
Ogni angolo esterno di un triangolo
è maggiore di ciascuno degli angoli
interni a esso non adiacenti.
Relazioni fra gli
angoli e i lati
di un triangolo
Se in un triangolo due lati non sono
congruenti, allora anche gli angoli
opposti non sono congruenti e al
lato maggiore sta opposto l’angolo
maggiore.
Analogamente, se in un triangolo
due angoli non sono congruenti,
allora anche i lati opposti non sono
congruenti e all’angolo maggiore
sta opposto il lato maggiore.
Disuguaglianza
triangolare
Ogni lato di un triangolo è minore
della somma degli altri due
e maggiore della loro differenza
(la differenza, naturalmente, va
effettuata sottraendo dal lato
maggiore il lato minore).
IN SIMBOLI
α
γ
β
α
c
b
β
>
>
> ¼) a > b
a > b ¼) > γ
a
b
c
a
bc <a <bþc
ac <b<aþc
ab<c <aþb
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
TEOREMA
2/8
Scheda
16
Scheda per il recupero 16
B Verifica delle conoscenze
Congruenza nei triangoli
Vero o falso?
1
un triangolo è l’intersezione di tre semipiani
V
F
2
ogni triangolo è convesso
V
F
3
ogni triangolo scaleno è ottusangolo
V
F
4
ogni triangolo isoscele è acutangolo
V
F
5
ogni triangolo equilatero è anche isoscele
V
F
6
ogni triangolo isoscele è anche equilatero
V
F
7
due triangoli equilateri con un lato rispettivamente congruente sono congruenti
V
F
8
due triangoli rettangoli isosceli con le ipotenuse congruenti sono sempre congruenti
V
F
9
due triangoli con due angoli rispettivamente congruenti sono sempre congruenti
V
F
10 due triangoli rettangoli isosceli con un cateto rispettivamente congruente sono sempre congruenti
V
F
11 due triangoli rettangoli con un cateto rispettivamente congruente sono sempre congruenti
V
F
12 due triangoli rettangoli con i due cateti rispettivamente congruenti sono sempre congruenti
V
F
Test
13 Nei triangoli ABC e A0 B 0 C 0 , nella figura qui sotto, gli elementi contrassegnati con lo stesso simbolo sono congruen-
ti. Quale delle seguenti affermazioni è corretta?
A
A
I due triangoli sono congruenti in base al primo criterio di congruenza
B
I due triangoli sono congruenti in base al secondo criterio di congruenza
C
I due triangoli sono congruenti in base al terzo criterio di congruenza
D
I due triangoli possono non essere congruenti
B
A'
C
B'
C'
14 Nei triangoli ABC e A0 B0 C0 , nella figura qui sotto, gli elementi contrassegnati con lo stesso simbolo sono congruenti.
Quale delle seguenti affermazioni è corretta?
A
I due triangoli sono congruenti in base al primo criterio di congruenza
B
I due triangoli sono congruenti in base al secondo criterio di congruenza
C
I due triangoli sono congruenti in base al terzo criterio di congruenza
D
I due triangoli possono non essere congruenti
B
A'
C
B'
C'
15 Affinché due triangoli siano congruenti, avere un lato e gli angoli a esso adiacenti ordinatamente congruenti è una
condizione:
A
necessaria ma non sufficiente
B
sufficiente ma non necessaria
C
necessaria e sufficiente
D
né necessaria né sufficiente
16 Affinché due triangoli siano congruenti, avere gli angoli ordinatamente congruenti è una condizione:
A
necessaria ma non sufficiente
B
sufficiente ma non necessaria
C
necessaria e sufficiente
D
né necessaria né sufficiente
17 Affinché due triangoli siano congruenti, avere i lati ordinatamente congruenti è una condizione:
A
necessaria ma non sufficiente
B
sufficiente ma non necessaria
C
necessaria e sufficiente
D
né necessaria né sufficiente
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
A
3/8
Scheda
16
Scheda per il recupero 16
C Esercizi guidati
Congruenza nei triangoli
Negli esercizi 1-2-3, fai riferimento al seguente teorema: «sia APB un triangolo; prolunga BP, dalla parte di
P, di un segmento PD congruente a BP; prolunga AP, dalla parte di P, di un segmento PC congruente ad AP.
Dimostra che AB ffi CD e BC ffi AD».
1 Individua l’ipotesi e la tesi del teorema e contrassegna nella figura con uno stesso simbolo gli elementi che sono
congruenti per ipotesi:
D
C
IPOTESI:
..............................
TESI:
..............................
P
A
2
B
Completa le parti mancanti e indica con una crocetta le risposte corrette.
a. Nei due triangoli APD e BPC, per quale ragione risulta AP ffi ..... e DP ffi .....?
Per ipotesi
Perché somme di segmenti congruenti
Perché elementi corrispondenti in triangoli congruenti
b. Nei due triangoli APD e BPC, per quale ragione risulta APbD ffi CPbB?
Per ipotesi
Perché opposti al vertice
Perché elementi corrispondenti in triangoli congruenti
c. In base a quale criterio i due triangoli APD e BPC sono congruenti?
Primo criterio di congruenza
Secondo criterio di congruenza
Terzo criterio di congruenza
d. Dal punto c. segue che AD ffi ..... Per quale ragione?
Per ipotesi
Per i criteri di congruenza dei triangoli
Perché elementi corrispondenti in triangoli congruenti
f. Dal punto e. segue che AB ffi ..... Per quale ragione?
Per ipotesi
Per i criteri di congruenza dei triangoli
Perché elementi corrispondenti in triangoli congruenti
3 Scrivi in forma discorsiva la dimostrazione del teorema di cui nell’esercizio 1 hai espresso ipotesi e tesi, tenendo
conto dei passi suggeriti nell’esercizio precedente.
Negli esercizi 4-5-6, fai riferimento al teorema che ha come modello la figura qui sotto, l’ipotesi e la tesi qui
C
di seguito.
IPOTESI:
TESI:
bB ffi DC
bB, AC ffi BC e CM ffi CD
AM ffi MB, M C
b
b
CAM ffi CBD
D
A
4
M
B
Completa il seguente enunciato a parole del teorema corrispondente all’ipotesi e alla tesi indicate.
«Dato un triangolo ABC, ......................... sulla base AB, sia CM la .................................................. . Un triangolo BCD è tale che BC è la
bisettrice di ............... e .............................. . Dimostra che ..............................».
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
e. In base a quale criterio i due triangoli APB e CPD sono congruenti?
Primo criterio di congruenza
Secondo criterio di congruenza
Terzo criterio di congruenza
4/8
16
Scheda
5
Scheda per il recupero 16
C Esercizi guidati
Congruenza nei triangoli
Completa le parti mancanti e indica con una crocetta la risposta corretta.
a. In base a quale criterio i triangoli CMA e CMB sono congruenti?
Primo criterio di congruenza
Secondo criterio di congruenza
Terzo criterio di congruenza
Proprietà transitiva della congruenza
b. In base a quale criterio i triangoli CMB e CBD sono congruenti?
Primo criterio di congruenza
Secondo criterio di congruenza
Terzo criterio di congruenza
Proprietà transitiva della congruenza
c. Da a. e b. segue che il triangolo CMA è congruente al triangolo CBD. Per quale ragione?
Primo criterio di congruenza
Secondo criterio di congruenza
Terzo criterio di congruenza
Proprietà transitiva della congruenza
bM ffi :::::::::: Per quale ragione?
d. Dal punto c. segue che CA
Per ipotesi
Per i criteri di congruenza dei triangoli
Perché elementi corrispondenti in triangoli congruenti
6 Riscrivi la dimostrazione del teorema espresso nell’esercizio 4 in forma discorsiva, tenendo conto dei passi suggeriti
nell’esercizio precedente.
C
7 Fai riferimento alla figura qui a fianco (P è un punto interno al triangolo ABC).
a. Prolunga AP e indica con Q il suo punto d’intersezione con il lato BC.
bB. A quale
b. In base al teorema dell’angolo esterno, puoi affermare che APbB > AQ
triangolo è stato applicato il teorema?
APB
AQB
PQB
P
B
A
AQC
c. In base al teorema dell’angolo esterno applicato al triangolo AQC, puoi dire che:
bB? ..............................
d. In base a quanto dimostrato in b. e c., che cosa puoi concludere a proposito degli angoli APbB e AC
Negli esercizi 8-9, fai riferimento al seguente teorema: «Sia ACBC 0 un quadrilatero in cui AC ffi AC 0 e
BC ffi BC 0 . Dimostra che l’angolo esterno di vertice C è maggiore di ciascuno dei due angoli in cui la diagonale AB divide l’angolo C AbC 0 ».
8
IPOTESI:
TESI:
9
C
In riferimento alla figura qui a fianco, riscrivi in simboli l’ipotesi e la tesi del teorema.
e ...............
.................... e .............................................
....................
Completa la seguente dimostrazione guidata del teorema.
a. In base al teorema ................................... applicato al triangolo ......................... puoi dire che:
> ..........
b. I due triangoli ABC e ABC0 sono ............... per il .................... criterio di congruenza; in particolare:
..........
ffi
quindi è anche:
> ..........
A
β
γ
α
B
C'
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
bB > ..........
b B > .......... e AQ
AQ
5/8
16
Scheda
Scheda per il recupero 16
C Esercizi guidati
Congruenza nei triangoli
Negli esercizi 10-11, fai riferimento al teorema che ha come modello la figura sotto, l’ipotesi e la tesi riportate di seguito.
C
IPOTESI:
TESI:
bB < ABbC
CA
BC < PA þ PC
P
A
B
10 Completa il seguente enunciato a parole del teorema corrispondente all’ipotesi e alla tesi indicate.
«Sia ABC un triangolo e P un punto .................... al triangolo; dimostra che, se .............................., allora il segmento BC è minore
della somma delle .................... di P da ....................».
11 Completa la seguente dimostrazione guidata del teorema.
bB < ABbC, puoi dedurre che:
a. Dall’ipotesi CA
BC < ..........
b. Per la disuguaglianza triangolare applicata al triangolo APC, puoi dedurre che:
AC < ..........
c. Confrontando le due disuguaglianze, ottieni che:
BC < .......... < ..........
e quindi .............................. .
12 Completa la seguente tabella, in cui ti guidiamo a dimostrare un teorema.
Passi
bb, conduci la bisettrice r dell’angolo. Considera un punto P su tale
Dato un angolo aO
bisettrice e traccia due semirette, aventi origine in P, e giacenti in semipiani opposti rispetto
alla bisettrice, che formano con OP angoli congruenti. Indica con Q e R, rispettivamente, i
punti d’intersezione di tali semirette con a e b. Sia S un punto di OP; dimostra che RS ffi QS.
Figura
Q
a
S
O
P
r
b
Ipotesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::
Tesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::
Dimostrazione
I due triangoli OPQ e ::::::::::::::: hanno:
OP
in comune
::::::::::
ffi ::::::::::
per ipotesi
::::::::::
ffi ::::::::::
per ::::::::::
quindi sono congruenti per il ::::::::::::::::::::::::::::::. In particolare, PQ ffi :::::::::: .
I due triangoli PQS e ::::::::::::::: hanno:
PS
::::::::::
in comune
ffi ::::::::::
PQ ffi ::::::::::
per ipotesi
per la precedente dimostrazione
Pertanto sono congruenti per il ::::::::::::::::::::::::::::::::::::::::; in particolare RS ffi :::::::::: .
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
R
6/8
Scheda
16
Scheda per il recupero 16
C Esercizi guidati
Congruenza nei triangoli
13 Completa la seguente tabella, in cui ti guidiamo a dimostrare un teorema.
Passi
In un triangolo ABC, isoscele sulla base AB, traccia le mediane AM e BN. Indica con P il loro
punto d’intersezione e dimostra che il triangolo APB è isoscele sulla base AB.
Figura
C
N
Ipotesi
AC ffi ::::::::::
Tesi
AP ffi ::::::::::
AN ffi ::::::::::
P
M
A
B
BM ffi ::::::::::
fP g ¼ AM \ ::::::::::
I due triangoli ABN e ABM hanno:
Dimostrazione
AN ffi BM
in quanto ::::::::::::::::::::::::::::::::::::::::
AB
bB ffi CBbA
CA
in comune
perché :::::::::::::::::::::::::::::::::::::::::::::
Pertanto i due triangoli sono :::::::::::::::::::: per il ::::::::::::::::::::::::: .
bB ffi :::::::::::::::
In particolare M A
bB ffi ::::::::::::::: , quindi il triangolo APB è ::::::::::
Da quanto appena dimostrato, segue che P A
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::.
16
D Esercizi da svolgere
bC. Siano Q e R, rispettivamente, i punti appartenenti ad AB e ad
Dato un triangolo ABC, sia AP la bisettrice di BA
b
b
AC, tali che AP Q ffi AP R. Dimostra che AQ ffi AR.
1
Dato un triangolo ABC, isoscele sulla base BC, prolunga AB, dalla parte di A, di un segmento AE, e AC, dalla parte di
A, di un segmento AD, in modo che AD ffi AE. Dimostra che BD ffi EC.
2
Dato un triangolo ABC, isoscele sulla base AB, disegna, esternamente al triangolo ABC, un triangolo ABD, isoscele
sulla base AB. Considera un punto qualsiasi P sul segmento CD e dimostra che PA ffi PB.
3
4 Dimostra che il triangolo che si ottiene congiungendo i punti medi dei lati di un triangolo isoscele è anch’esso
isoscele.
5 Sia ABC un triangolo isoscele sulla base AB. Sul prolungamento di CA dalla parte di A considera un punto P e sul
prolungamento di CB dalla parte di B un punto Q, in modo che AP ffi BQ. Dimostra che AQ ffi BP.
6 Sia ABC un triangolo rettangolo di ipotenusa BC. Prolunga il cateto AB, dalla parte di A, di un segmento AP ffi AB e
b C.
l’ipotenusa BC, dalla parte di C, di un segmento CQ ffi BC. Dimostra che CPbQ ffi P Q
7
Dimostra che, in due triangoli congruenti, le due bisettrici relative a due angoli congruenti sono congruenti.
8 Sia ABC un triangolo isoscele sulla base AB. Indica con N e M, rispettivamente i punti medi di AC e BC. Considera
un punto P sull’altezza del triangolo relativa ad AB e dimostra che i due segmenti PN e PM sono congruenti.
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
Scheda
7/8
Scheda
16
Scheda per il recupero 16
D Esercizi da svolgere
Congruenza nei triangoli
In un triangolo ABC, isoscele sulla base AB, considera un punto P su AC e un punto Q su BC, in modo che
CP ffi CQ. Detto R il punto d’intersezione di BP e di AQ, dimostra, nell’ordine che:
9
a. il triangolo ABR è isoscele sulla base AB;
b. i triangoli ACR e BCR sono congruenti;
bB.
c. la semiretta CR è la bisettrice di AC
10 In un triangolo ABC, isoscele sulla base AB, traccia l’altezza CH. Considera un qualsiasi punto P su CH e dimostra
che PA ffi PB.
11 In riferimento alla figura qui sotto, rispondi alle seguenti domande.
a. Qual è l’ampiezza di ABbC?
b. Quale fra i tre lati del triangolo ABC ha lunghezza minima? Perché?
c. Quale fra i tre lati del triangolo ABC ha lunghezza massima? Perché?
C
55°
115°
60°
A
B
D
12 Può esistere un triangolo i cui lati sono lunghi 10 cm, 12 cm e 15 cm? E un triangolo i cui lati sono lunghi 7 cm,
11 cm e 3 cm? Giustifica le tue risposte.
13 Sia ABC un triangolo isoscele sulla base AB e P un punto interno a BC. Dimostra che PA > PB.
14 Sia ABCD un quadrilatero convesso. Dimostra che ciascun lato è minore della somma di tutti gli altri.
(Suggerimento: traccia una delle due diagonali di ABCD)
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
8/8