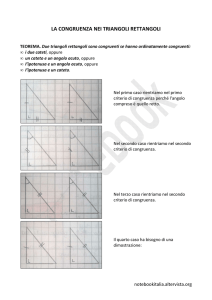
IL TERZO CRITERIO
DI CONGRUENZA DEI TRIANGOLI
Due triangoli sono congruenti se hanno i tre lati ordinatamente congruenti.
Hp
≅ ′′
≅ ≅ ′′
Th
≅ ′′′
Dimostrazione
Dal vertice B e nel semipiano opposto a quello del triangolo rispetto alla retta del lato ,
, su tale semiretta
tracciamo una semiretta che formi con un angolo congruente a ′
e tracciamo il segmento prendiamo un punto A′′′′ in modo che ′′ ≅ ′′
′′. Il triangolo
′′èè congruente al triangolo′′′
triangolo
per il primo criterio di congruenza.
Tracciamo il segmento ′′, si ha che:
≅ • poiché ′′ e ′′ ≅
≅ ′′ (proprietà
′′ allora transitiva della congruenza)
e ≅ • poiché ′′ ′′
≅ ′′
allora (proprietà
transitiva della congruenza).
I triangoli ′′e ′′
sono dunque
isosceli e quindi ′′ ≅ ′′ e
′′ ≅ ′′.
Allora ≅ ′′ perché somme di angoli uguali. Torniamo a considerare i triangoli
e ′′,, di essi sappiamo che:
notebookitalia.altervista.org
≅ ′′
≅ ′′
≅ ′′
Essi sono congruenti per il primo criterio di congruenza. In definitiva ≅ ′′,
′′ ≅ ′′′ per costruzione, quindi ≅ ′′′ per la proprietà transitiva, come
volevasi dimostrare.
notebookitalia.altervista.org