Facoltà di ECONOMIA – Università di Pavia – 15 Aprile 2009
Prova scritta di Analisi dei dati, Modalità C
• Riportare sul foglio nome, cognome, numero di matricola e modalità del
testo d’esame.
Problema 1 (8 PUNTI)
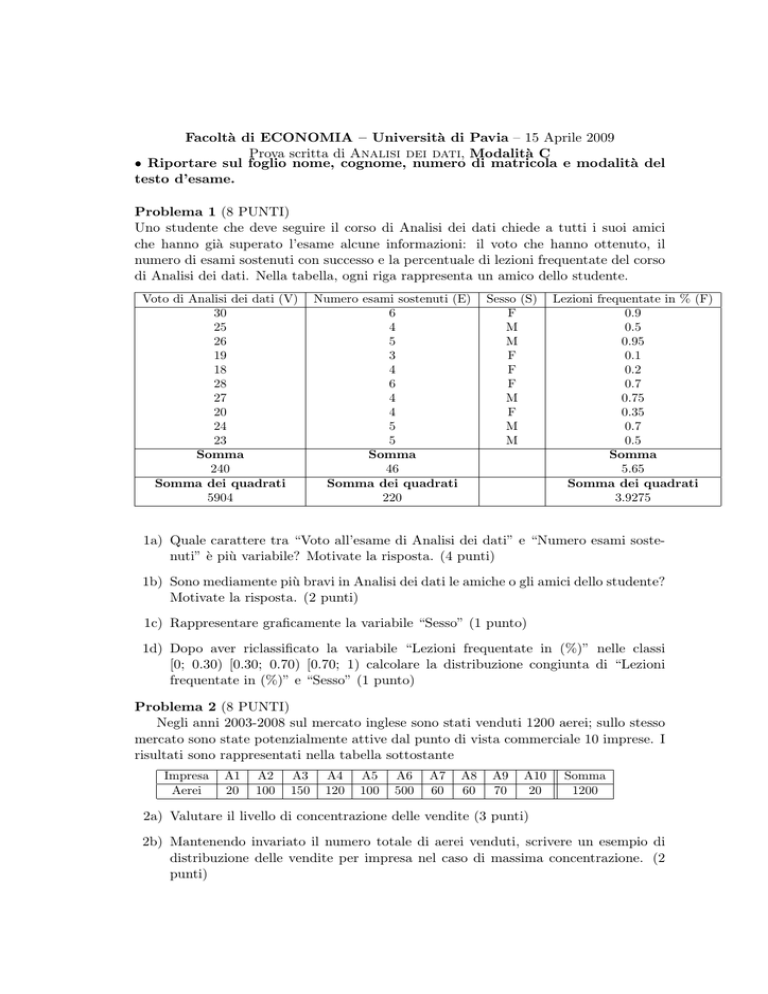
Uno studente che deve seguire il corso di Analisi dei dati chiede a tutti i suoi amici
che hanno già superato l’esame alcune informazioni: il voto che hanno ottenuto, il
numero di esami sostenuti con successo e la percentuale di lezioni frequentate del corso
di Analisi dei dati. Nella tabella, ogni riga rappresenta un amico dello studente.
Voto di Analisi dei dati (V)
30
25
26
19
18
28
27
20
24
23
Somma
240
Somma dei quadrati
5904
Numero esami sostenuti (E)
6
4
5
3
4
6
4
4
5
5
Somma
46
Somma dei quadrati
220
Sesso (S)
F
M
M
F
F
F
M
F
M
M
Lezioni frequentate in % (F)
0.9
0.5
0.95
0.1
0.2
0.7
0.75
0.35
0.7
0.5
Somma
5.65
Somma dei quadrati
3.9275
1a) Quale carattere tra “Voto all’esame di Analisi dei dati” e “Numero esami sostenuti” è più variabile? Motivate la risposta. (4 punti)
1b) Sono mediamente più bravi in Analisi dei dati le amiche o gli amici dello studente?
Motivate la risposta. (2 punti)
1c) Rappresentare graficamente la variabile “Sesso” (1 punto)
1d) Dopo aver riclassificato la variabile “Lezioni frequentate in (%)” nelle classi
[0; 0.30) [0.30; 0.70) [0.70; 1) calcolare la distribuzione congiunta di “Lezioni
frequentate in (%)” e “Sesso” (1 punto)
Problema 2 (8 PUNTI)
Negli anni 2003-2008 sul mercato inglese sono stati venduti 1200 aerei; sullo stesso
mercato sono state potenzialmente attive dal punto di vista commerciale 10 imprese. I
risultati sono rappresentati nella tabella sottostante
Impresa
Aerei
A1
20
A2
100
A3
150
A4
120
A5
100
A6
500
A7
60
A8
60
A9
70
A10
20
Somma
1200
2a) Valutare il livello di concentrazione delle vendite (3 punti)
2b) Mantenendo invariato il numero totale di aerei venduti, scrivere un esempio di
distribuzione delle vendite per impresa nel caso di massima concentrazione. (2
punti)
2c) Mostrare che
1
N
essendo µXY =
PN
i=1 [xi − µX ] [yi − µY ] =
PN Xi
Xi ×Yi
i=1
i=1 N
N , µX =
PN
µXY − µX µY ,
P
Yi
e µY = N
i=1 N . (3 punti)
Problema 3 (9 PUNTI)
3a) Due fratelli sono diventati titolari di un concessione ventennale. Sapendo che alla
loro età la probabilità di sopravvivere dopo 20 anni è pari a 0.80 e 0.70, calcolare,
supponendo che gli eventi siano indipendenti, la probabilità:
i) che sopravvivano entrambi dopo 20 anni;
ii) che sopravviva solo il secondo fratello (3 punti)
3b) Siano A e B due eventi tali che P (A ∪ B) = 0.7, P (A) = 0.5 e P (B) = 0.3.
Calcolare P (A|B), dire inoltre se i due eventi sono incompatibili. (3 punti)
3c) Enunciare il teorema di Bayes (3 punti)
Problema 4 (5 PUNTI)
La distribuzione dell’ammontare in euro speso da 100 individui che hanno trascorso
fuori casa le vacanze di Pasqua può essere reppresentata dal seguente box-plot
4a) La distribuzione è simmetrica? Stabilire se la media è più piccola o più grande
della mediana. Commentare il risultato (3 punti)
4b) Dire se sono presenti dati anomali (outliers). Motivare la risposta. (2 punti)
Facoltà di ECONOMIA – Università di Pavia – 15 Aprile 2009
Prova scritta di Analisi dei dati, Modalità D
• Riportare sul foglio nome, cognome, numero di matricola e modalità del
testo d’esame.
Problema 1 (8 PUNTI)
Una società che si occupa di ricerche di mercato ha effettuato, per un bar nelle vicinanze della facoltà di Scienze Politiche, un’indagine di customer satisfaction. Sono stati
intervistati 10 clienti dopo che hanno consumato il pranzo. La soddisfazione è espressa
in una scala numerica crescente che va da 1 a 10.
Soddisfazione (SO)
7
8
4
9
3
7
5
9
7
10
Somma
69
Somma dei quadrati
523
Sesso (S)
M
M
F
M
F
M
F
F
M
F
Frequenza di visita nell’ultimo mese (F)
6
7
2
5
5
7
8
3
2
6
Somma
51
Somma dei quadrati
301
Età (E)
19
21
18
19
19
22
20
25
21
20
Somma
204
Somma dei quadrati
4198
1a) Calcolare media e mediana di Soddisfazione ( 2 punti)
1b) Quale carattere tra Frequenza di visita nell’ultimo mese ed Età è più variabile?
Motivare la risposta. (4 punti)
1c) È vero che le ragazze che hanno risposto all’intervista sono mediamente più
soddisfatte degli intervistati di sesso maschile? Giustificate la risposta. (2 punti)
Problema 2 (8 PUNTI)
Negli anni 2003-2008 sul mercato europeo sono state vendute 250 navi da crociera;
sullo stesso mercato sono state potenzialmente attive dal punto di vista commerciale
10 imprese. I risultati sono rappresentati nella tabella sottostante
Impresa
Navi
A1
20
A2
10
A3
15
A4
10
A5
10
A6
50
A7
10
A8
40
A9
65
A10
20
Somma
250
2a) Valutare il livello di concentrazione delle vendite (3 punti)
2b) Mantenendo invariato il numero totale di navi vendute, scrivere un esempio di
distribuzione delle vendite per impresa nel caso di minima concentrazione (2
punti)
2c) Scrivere la definizione dell’indice di eterogeneita G0 , precisando attentamente le
quantità usate (3 punti).
Problema 3 (9 PUNTI)
3a) Due fratelli sono diventati titolari di un concessione ventennale. Sapendo che alla
loro età la probabilità di sopravvivere dopo 20 anni è pari a 0.70 e 0.60, calcolare,
supponendo che gli eventi siano indipendenti, la probabilità:
i) che nessuno dei due sopravviva dopo 20 anni;
ii) che sopravviva solo il primo fratello (3 punti)
3b) Siano A e B due eventi tali che P (A ∪ B) = 0.8, P (A) = 0.45 e P (B) = 0.4.
Calcolare P (B|A), dire inoltre se i due eventi sono indipendenti. (3 punti)
3c) Enunciare il teorema delle probabilità totali (3 punti)
Problema 4 (5 PUNTI)
La distribuzione dell’ammontare in euro speso da 100 individui che hanno trascorso
fuori casa le vacanze di Pasqua può essere rappresentata dal seguente box-plot
4a) La distribuzione è simmetrica? Stabilire se la media è più piccola o più grande
della mediana. Commentare il risultato (3 punti).
4b) Dire se sono presenti dati anomali (outliers). Motivare la risposta. (2 punti)