Attività progettuale 2
Titolo
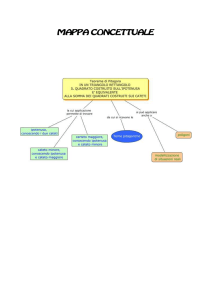
“Alla scoperta del teorema di Pitagora”
Parole chiave
Terna pitagorica; teorema
Competenze
chiave europee
Ø
Ø
Ø
Ø
Ø
Comunicazione nella madrelingua;
competenza matematica;
imparare a imparare;
competenze sociali e civiche;
spirito di iniziativa e intraprendenza.
Utenti destinatari
L’alunna F. B. (che presenta un disturbo evolutivo delle capacità
scolastiche non specificato - ICD- 10 F81.9 - soprattutto nelle
discipline logico-matematiche in soggetto borderline cognitivo)
e l’alunna F. N. (che presenta difficoltà nelle capacità
scolastiche in soggetto borderline cognitivo).
Classe
II A
Prerequisiti
disciplinari
Ø Conoscere le principali figure piane e le loro proprietà;
Ø conoscere i numeri reali;
Ø conoscere il concetto di estrazione di radice come
operatore inverso all’elevamento al quadrato;
Ø saper calcolare l’area di un quadrato;
Ø saper riconoscere figure equiscomponibili.
Obiettivi formativi
Ø Migliorare la capacità di osservazione e descrizione;
Ø migliorare le capacità di attenzione e concentrazione;
Ø promuovere l’autonomia nell’organizzazione del lavoro
da svolgere;
Ø promuovere un miglioramento nell’autostima;
Ø migliorare lo spirito di iniziativa nelle relazioni sociali.
Conoscenze/
Abilità
Ø Sviluppare la conoscenza della terna pitagorica;
Ø conoscere il teorema di Pitagora (formula diretta) e le sue
applicazioni al rettangolo;
Ø individuare una terna pitagorica;
Ø applicare le proprietà delle terne per individuare la misura
dell’ipotenusa, dati i due cateti (formula diretta);
Ø applicare il teorema di Pitagora ai triangoli rettangoli
individuabili nel rettangolo.
Competenze
Ø Risolvere semplici problemi applicando il teorema di
Pitagora.
Traguardi di
Ø Riconoscere e risolvere problemi in contesti diversi
competenze
valutando le informazioni e la loro coerenza;
Ø spiegare il procedimento seguito;
Ø rafforzare un atteggiamento positivo rispetto alla
matematica attraverso esperienze significative e capire
come gli strumenti matematici appresi siano utili in molte
situazioni per operare nella realtà.
Collegamenti
interdisciplinari
Ø Storia: gli antichi Egizi;
Ø tecnologia: costruzione geometrica del triangolo con
utilizzo degli strumenti.
Metodologia
Ø Brainstorming;
Ø lezione
interattiva
mediante
un
approccio
ludico/operativo con momenti che prevedono la visione di
brevi video, attività pragmatiche con agganci operativi;
Ø didattica laboratoriale;
Ø brevi momenti riepilogativi di lezione frontale;
Ø si promuoverà, inoltre, il cooperative learningche darà
spazio al dialogo e al confronto per far sì che le due
alunne gestiscano le diverse attività sintonizzandosi col
gruppo;
Ø riorganizzazione dei contenuti mediante immagini e
semplici mappeconcettuali procedurali;
Ø feedback per avere conferma di quanto ascoltato e letto;
Ø problem solving;
Ø learning by doing;
Ø peer education.
Strumenti
Ø
Ø
Ø
Ø
Ø
Ø
Ø
Ambiente di
lavoro
Ø Aula;
Ø aula trasformata in laboratorio;
Ø laboratorio informatico.
Svolgimento
dell’attività
Libro di testo (recupero);
computer;
schede semplificate;
mediatori iconici (immagini, video);
materiale manipolativo;
corda;
strumenti compensativi (calcolatrice, tavola numerica,
mappa della procedura della risoluzione dei problemi:
task analysis);
Ø mappa concettuale procedurale.
L’attività sarà svolta in due lezioni (da due ore ciascuna) così
suddivise:
Prima ora:
Ø 5 minuti: motivazione attraverso l’elicitazione delle
conoscenze pregresse (classificazione dei triangoli, diversi
tipi di angolo) e la stimolazione dell’expectancygrammar,
della capacità, cioè, di prevedere;
Ø 5 minuti: introduzione del nucleo tematico tramite la
visione insieme al resto della classe di un brevissimo
video: “Il teorema di Pitagora: la storia di una semplice
dimostrazione”, che propone un breve excursus storico e
mostra come, nella leggenda, Pitagora abbia maturato
l’idea del suo teorema osservando le piastrelle del
pavimento del palazzo del tiranno Policrate;
Ø 5 minuti: riflessione su quanto visto (comprensione
globale);
Ø 5 minuti: data la difficoltà dell’argomento si sceglie di
offrire un’esposizione multipla dei contenuti e si procede
con la lettura di alcune pagine del tredicesimo capitolo
(“Le cioccolate di Pitagora”) di “I magnifici diecil’avventura di un bambino nel mondo della matematica”
di Anna Cesaroli, che parte dalle terne pitagoriche per
spiegare il teorema attraverso la cioccolata;
Ø 10 minuti: la comprensione globale prosegue con
l’esplorazione delle parole chiave (terna pitagorica,
teorema), seguita dal disegno dei quadrati di cioccolata;
Ø 15 minuti: si realizza, poi, con il gruppo classe un
triangolo rettangolo con una corda;
Ø 15 minuti: esecuzione guidata di esercizi sulla terna
pitagorica.
Seconda ora:
Ø 5 minuti: A tutta la classe, suddivisa in gruppi da
quattro, si distribuisce una scheda che richiede di
costruire, dati dei numeri, delle terne pitagoriche. Le due
alunne vengono inserite in due gruppi diversi;
Ø 15 minuti: dopo aver presentato l’attività e i criteri di
valutazione della stessa, si parte. I quattro gruppi, stabiliti
i
ruoli
di
ciascun
membro,
si
cimentano
nell’individuazione delle cinque possibili terne; segue la
correzione dei lavori di gruppo e una riflessione
sull’operato;
Ø 5 minuti: visione del brevissimo video “Teorema di
Pitagora: dimostrazione con i chicchi di riso”, che,
attraverso l’immagine del riso che scorre da un quadrato
all’altro, dimostra in maniera molto semplice il teorema;
Ø 15 minuti: esplorazione analitica dell’enunciato del
teorema di Pitagora. Costruzione di una semplice mappa
procedurale che servirà da strumento compensativo nel
caso in cui le alunne non memorizzassero la formula;
Ø 20 minuti: risoluzione guidata di semplici problemi
diretti sulla relazione tra cateti e ipotenusa (mappa della
procedura di risoluzione dei problemi geometrici basata
sulla task analysis).
Terza ora:
Ø 10 minuti: correzione dei problemi assegnati a casa per
avere un feedback su quanto presentato;
Ø 10 minuti: ricerca dei triangoli rettangoli nella figura
piana del rettangolo e osservazione dell’ambiente
circostante;
Ø 40 minuti: risoluzione guidata di problemi applicati allo
spazio dell’aula i cui risultati possono essere controllati
attraverso strumenti di misurazione;
Quarta ora:
Ø 60 minuti: verifica sommativa (completamento di una
tabella; risoluzione di un problema con applicazione del
teorema di Pitagora).
Verifica
Ø La verifica scritta terrà conto dei tempi più lunghi e le
richieste saranno chiare e non plurime; sarà consentito, se
le alunne lo riterranno necessario, l’uso di mediatori
didattici (mappa procedurale, schemi, tabelle) e di
strumenti compensativi quali la calcolatrice, la tavola
numerica;
Ø rubrica valutativa.
Valutazione
Ø Come esplicitato nel PEI, il momento della valutazione
formativa sarà visto come incentivo al perseguimento
dell’obiettivo del massimo possibile sviluppo della
personalità; la valutazione sommativa sarà, invece,intesa
come valutazione complessiva dei progressi compiuti
dalle alunne in relazione sia ai traguardi considerati, che
al grado di maturazione globale della personalità.
Ø Gli alunni saranno, inoltre, coinvolti, in un’attività di
autovalutazione, esprimendo un giudizio motivato sul
loro lavoro.
Monitoraggio
Si attueranno attività di monitoraggio volte ad evidenziare i
punti di forza e di criticità delle attività svolte.
Percorsi di
miglioramento
Riorganizzazione dell’attività in prospettiva migliorativa
considerati i risultati del monitoraggio e delle verifiche.