Document

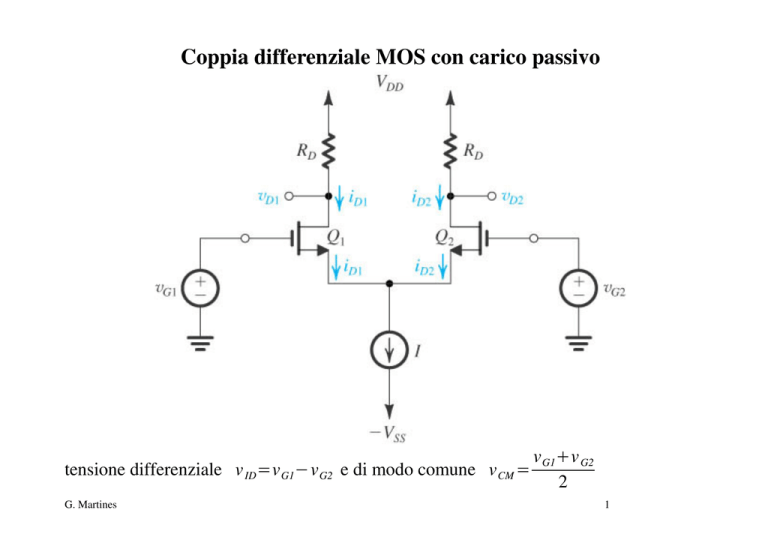
Coppia differenziale MOS con carico passivo
tensione differenziale v ID =v G1v G2
G. Martines
v G1+v G2
e di modo comune v CM =
2
1
Coppia differenziale MOS con carico passivo
Funzionamento con segnale di modo comune
I
vCM max = Vt + VDD − R D
2
vCM min = −VSS + VCS + Vt + VOV
con VCS tensione minima per il
corretto funzionamento del
generatore.
Nota: VOV rappresenta la tensione
di overdrive cioè
VOV = VGS − Vt
G. Martines
2
Coppia differenziale MOS con carico passivo
Funzionamento con segnale differenziale
v idmax =v GS1+v S =√ 2 V OV
G. Martines
Nell'ipotesi di transistori uguali.
Se vid = 0 allora vGS1= vGS2.
Se vid cresce, allora vS cresce e VGS2 deve
diminuire e quindi iD2 diminuisce di ∆I
mentre iD1 cresce di ∆I perché la somma è
I (costante).
Come conseguenza vD1 diminuisce di di
∆IRD e vD2 aumenta della stessa quantità
perché anche le RD sono uguali.
Il processo termina quando v S =V t
poiché iD2 si annulla e i D1= I .
Se si indica con VOV la tensione di
overdrive corrispondente a I/2 allora
v GS1=V t + √ 2 V OV e quindi
. Il circuito funziona come amplificatore per
√ 2 V OV ≤v id ≤ √ 2 V OV
3
Transcaratteristica
della coppia
differenziale MOS
Dalla espressione della
corrente in pinch-off si
ottiene
KN
√ i D1√ i D2= 2 v id
elevando al quadrato si può
introdurre I nella
espressione
Kn 2
2 √ i D1 i D2= I v
2 id
e quindi si può scrivere
√
√
( )
v /2
I
I v id
i D1 ,2= ±
1 id
2 V OV 2
V OV
G. Martines
2
che per
v id
≪V OV diviene
2
id =
I
V OV
v id
2
4
Transcaratteristica della coppia differenziale MOS
Il campo di linearità può essere aumentato aumentando la VOV ma questo implica
aumentare I e quindi diminuire il fattore di amplificazione µf ed il guadagno di tensione.
G. Martines
5
Guadagno differenziale
Il segnale differenziale viene applicato in modo bilanciato o
complementare.
VCM è la tensione continua che nasce dalla polarizzazione.
Circuito equivalente per il segnale con g m=
G. Martines
2I D
I
=
V OV V OV
6
Guadagno differenziale
v o1,2
gm RD
=∓
Per uscita single-ended
v id
2
v o2 v o1
per uscita differenziale Ad ≡
= g m RD
v id
Il metodo del mezzo circuito differenziale :
Un esempio di
calcolo:
Ad =g m ( R D / /r o )
Un esempio di
applicazione circuitale
G. Martines
7
Guadagno di modo comune
È zero se il generatore di corrente è ideale.
Altrimenti il circuito equivalente per il
segnale è:
Per effetto del segnale vicm nasce una corrente (2i) nel ramo del generatore di corrente.
G. Martines
8
Guadagno di modo comune
Per il calcolo si usa il mezzo circuito di
modo comune:
v o1 v o1
g m RD
R
=
=
≈ D
v icm v icm
1+ g m 2 R SS
2R SS
quindi per una uscita single-ended
RD
e CMRR=g m R SS
∣Acm∣≈
2R SS
Ma per l'uscita differenziale è Acm=0 .
Una dissimmetria sulle RD genera un
Acm non nullo anche se l'uscita è
differenziale:
∆ RD RD ∆ RD
∣Acm∣≈
=
2R SS 2R SS R D
( )
( )
RD ∆ g m
Analogamente per dissimmetria sulle gm ∣Acm∣≈
2R SS g m
G. Martines
9
Tensione di offset della coppia differenziale
In assenza di segnali applicati, la differenza nei valori
delle RD e delle correnti ID (a pari VGS , transistori non
identici hanno ID diverse) generano una tensione di
uscita differenziale
diversa da zero. Per
annullarla è necessario applicare una
tensione VOS che si
definisce tensione di
offset di ingresso
V
V OS = O
Ad
per il caso in esame si può scrivere:
√(
V OS =
G. Martines
)(
2
)
2
V OV ∆ R D
V ∆(W / L)
2
+ OV
+(∆V t )
2 RD
2 (W / L)
10
Esempio di coppia differenziale CMOS con carico attivo
il carico su ognuno dei rami è un generatore a
specchio di corrente che genera I/2. Generalmente
anche il generatore I è
uno specchio di corrente
e si usa la stessa
corrente di riferimento
per tutti i generatori.
Dall'analisi con il mezzo
circuito differenziale
Ad ≡
G. Martines
v od
=g m1 (r o1 / / r o3 )
v id
11
Esempio di coppia differenziale cascode
I transistori Q5 e Q7 costituiscono un generatore
di corrente cascode con il ramo della corrente di
riferimento qui non
disegnato (analogamente per Q6 e Q8).
I transistori Q1 e Q3
sono una configurazione cascode cioè
una CS in cascata
con una CG (analogamente per Q2 e
Q4). Essendo
Ron=( g m3 r o3 )r o1
Rop =( g m5 r o5 ) r o7
si ottiene la espressione del guadagno
Ad = g m1 ( Ron / / Rop )
G. Martines
12
Coppia differenziale CMOS single-ended con specchio di corrente
Principio di funzionamento:
in assenza
di segnale
Nell'ipotesi di transistori tutti uguali saranno uguali sia
le correnti che le tensioni e quindi V DS4=V DS3=V GS3 perchè Q3 è connesso a diodo.
La corrente di polarizzazione è uguale in tutti i transistori.
La corrente di uscita è nulla per il bilanciamento dei generatori di corrente.
G. Martines
13
Coppia differenziale CMOS single-ended con specchio di corrente
Principio di funzionamento:
circuito equivalente per un segnale
differenziale complementare
Trascurando le ro di tutti i transistori (tutti
identici per ipotesi) si ha
i= g m v id / 2
Per valutare l'equazione del guadagno di
tensione differenziale è però necessario
considerare le resistenze di uscita del modello a piccolo segnale dei transistori.
G. Martines
14
Coppia CMOS single-ended: Trans-conduttanza Gm in cortocircuito
dal modello equivalente per il segnale, separando i due rami:
v
g m1
v id
1
v g3 =g m1 id r o1 / / r o3 / /
quindi i o≈ g m4
ma essendo g m3=g m4 e
+ g m2
g m3
2
2
g m3
( )(
)
(
)
g m1=g m2 si conclude che G m≈ g m2 mentre senza lo specchio si ha G m≈g m2 /2
G. Martines
15
Coppia CMOS single-ended: Ro e guadagno differenziale Ad
Rin1 è quella di un CG realizzato con Q1:
r +1/ g m3 1
1
1
Rin1 = o1
≈
+
≈
1+ g m1 r o1 g m1 g m3 g m1 r o1 g m1
Ro2 è quella di un CG realizzato con Q2:
g m2
Ro2≈ r o2 (1+ g m2 Rin1 )≈r o2 (1+
)≈2r o2
g m1
essendo g m1=g m2 . Allora
v
2
1
1
1
i x =2i+ x =
+
vx=
+
vx
r o4 R o2 r o4
r o2 r o4
(
cioè
) (
)
Ro=r o2 / / r o4
Per il guadagno di tensione differenziale a vuoto si ottiene immediatamente:
A d =G m R o= g m2 (r o2 / / r o4 )
Nell'ipotesi ulteriore che r o2 =r o4 si riduce a
G. Martines
r o2 µ f
Ad = g m2 =
2
2
16
Coppia CMOS single-ended: Guadagno di modo comune Acm e CMRR
Dal circuito equivalente per il segnale di modo
comune si può dimostrare che:
vo
r o4
Acm≡
≈
v icm
2R SS (1+ g m3 r o3)
nelle ipotesi aggiuntive r o3 =r o4 e g m3 r o3 ≫1 :
1
Acm≈
2 g m3 RSS
Il rapporto di reiezione di modo comune allora vale:
∣A ∣
CMRR≡ d ≈ g m2 (r o2 / / r o4 )2 g m3 R SS
∣Acm∣
che ancora nelle ipotesi già dette diviene
2
CMRR≈ g m2 r o2 g m3 R SS ≈µ f .
G. Martines
17
G. Martines
18
Risposta in frequenza della coppia differenziale
Risposta per il segnale differenziale
C IN
G. Martines
Ad = g m (ro // RD )
1
fH =
2πC IN RS
= C gs + C gd [1 + g m (ro // R D )]
Risposta per il segnale di modo comune
 R  ∆R
ACM = − D  D
 2 RSS  R D
1
fZ =
2πC SS RSS
19
Risposta in frequenza della coppia differenziale
Risposta in frequenza del rapporto di reiezione di modo comune
G. Martines
20