Coppia differenziale con BJT e carico passivo

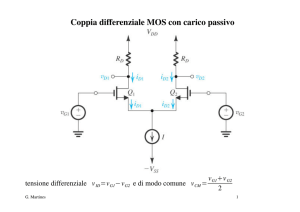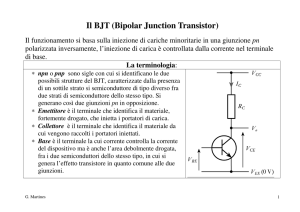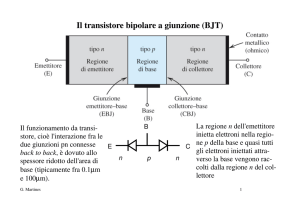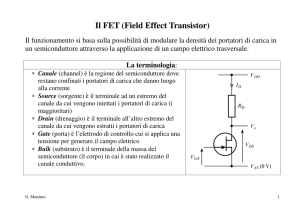
Coppia differenziale con BJT e carico passivo
tensione differenziale e di modo comune:
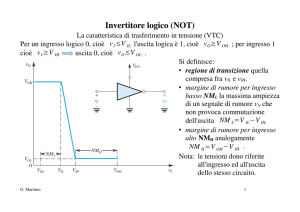
vd = vB1 − vB 2
G. Martines
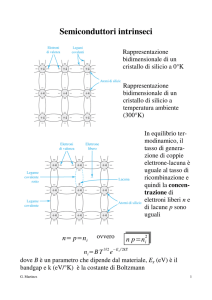
vCM =
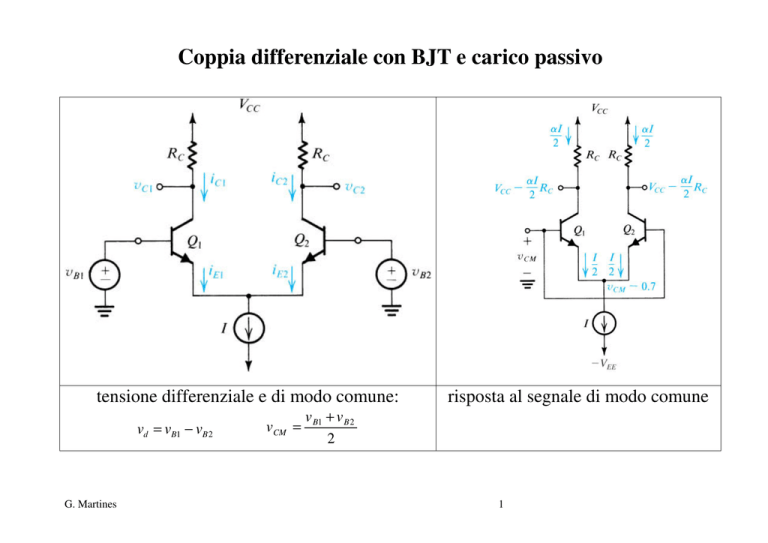
risposta al segnale di modo comune
v B1 + v B 2
2
1
Coppia differenziale con BJT e carico passivo
Saturazione dell’amplificatore per effetto del segnale differenziale (switch di corrente) e
escursione massima del segnale di uscita
G. Martines
2
Coppia differenziale con BJT e carico passivo
Risposta a piccolo segnale differenziale
G. Martines
3
Transcaratteristica di una coppia differenziale a BJT
Ipotesi: transistori identici
vBE
iC = I S e VT
iE = iC α
v BE = v B − v E I = I E1 + I E 2
poiché:
i

iE1  E 2 +1 = I
 i E1

ed
(v B 2 −v B1 )
iE 2
VT
=e
i E1
allora
I
i E1 =
(v B 2 −v B1 )
VT
1+ e
analogamente per iE2. Quindi
campo di funzionamento lineare limitato a ∆v B ≈ 4VT 1
approssimazione piccolo segnale valida con ∆v B < VT 2
1
infatti
iC1 =
− vd
1+ e
e 4 ≈ 54.6 e iC < 0.02αI
G. Martines
αI
4
VT
Analisi del funzionamento a piccolo segnale
Conviene esprimere le correnti di collettore con un equazione più comoda per la sostituzione del
termine esponenziale con il suo sviluppo in serie di potenze, moltiplicando numeratore e
vd
denominatore per il termine e
2VT
:
vd
iC1 =
αI
− vd
1+ e
αIe
=
VT
vd
e
2VT
2VT
− vd
+e
≈
αI 1 + vd 2V 

T

2
2VT
L’ultimo termine si è ottenuto sostituendo i termini esponenziali con il loro sviluppo in serie di
vd
potenze arrestato al primo termine e
2VT
= 1+
vd
2VT che vale per vd << 2VT. Allora si può
scrivere:
iC 1 ≈
αI
2
+
αI v d
2VT 2
= I C1 + ic1
iC 2 ≈
αI
2
−
αI v d
2VT 2
ed infine:
ic ≈
G. Martines
αI v d
2VT 2
= gm
vd
2
5
= I C 2 + ic 2
Analisi a piccolo segnale della coppia differenziale
G. Martines
6
Determinazione della resistenza differenziale di ingresso
G. Martines
7
Mezzo circuito equivalente di modo differenziale
Ipotesi: segnale applicato in modo complementare
G. Martines
8
Estensione delle prestazioni con RE
G. Martines
9
Effetti della reazione negativa generata dalle RE
sul guadagno e sulla impedenza di ingresso
G. Martines
10
Segnale di ingresso applicato in modo sbilanciato
G. Martines
11
Guadagno di tensione di modo comune
per uscita bilanciata
AC ≈ 0
Mezzo circuito equivalente di modo
comune
αRC
A
≈
−
per uscita sbilanciata C
2R
EE
αRC 
la formula esatta dal modello a piccolo segnale completo è AC ≈ − 2R
EE
G. Martines
12
 1
1
+
1 − 2 REE 

 βro αrµ


 .

Determinazione della resistenza di ingresso di modo comune
RiCM ≈
G. Martines
rµ
2
// (β + 1)REE // (β + 1)
ro
2
13
Tensione di offset della coppia differenziale
Per le dissimmetrie del circuito reale, si
rileva una tensione non nulla in uscita in
assenza di segnale di ingresso
G. Martines
La tensione di ingresso differenziale che
annulla la tensione di uscita dello
amplificatore, viene detta tensione di offset
riportata in ingresso
14
Effetti delle dissimmetrie sulla tensione di offset
Dissimmetria su RC:
definendo ∆RC = RC1 − RC 2 ed RC = (RC1 + RC 2 ) 2 si può scrivere
 ∆RC
α (I 2)∆RC
∆RC 
 αI 
VOS =
= VT 
VC1, 2 = VCC −   RC ±

e
quindi
Ad
2 
 2 
 RC \
Dissimmetria su IS:
definendo ∆I S = I S 1 − I S 2 ed I S = (I S 1 + I S 2 ) 2 si può scrivere
I  ∆I S 
 I  ∆I

I E1, 2 = 1 ±
VO = α   S RC
ed infine
2  2 I S  quindi
 2  IS
VOS



 ∆I S
= VT 
 IS



Poiché i due contributi sono incorrelati, per valutare correttamente la tensione di offset
 ∆R
VOS = VT  C
 RC \
G. Martines
2
  ∆I S
 + 
  IS



2
15
Correnti di polarizzazione e offset di corrente
I 2
I
I
=
=
B2
Se i transistori fossero identici lo sarebbero anche le correnti di base B1
β +1
∆β = β 1 − β 2
Considerando le differenze sui β e definendo
e β = (β 1 + β 2 ) 2
si può scrivere
I 2
I 1  ∆β 
1 m

I B1, 2 =
≈
β + 1 ± ∆β 2 2 β + 1 
β 
e quindi
 ∆β 
I 1  ∆β 

 = I B 

I OS =
2 β +1 β 
 β 
G. Martines
16
Coppia differenziale a BJT con carico attivo a specchio di corrente
G. Martines
17
Coppia differenziale a BJT con carico attivo a specchio di corrente
circuito equivalente a piccolo segnale per il calcolo di Gm
I
Gm = g m =
2VT
G. Martines
18
Coppia differenziale a BJT con carico attivo a specchio di corrente
circuito equivalente per il calcolo di Ro
La resistenza di carico complessiva
RO = ro 2 // ro 4
Il guadagno di tensione
differenziale:
Ad = Gm Ro
Nell’ipotesi di transistori con
eguale VA :
g r
1 VA
Ad = m o =
2
2 VT
G. Martines
19
Coppia differenziale a BJT con carico attivo a specchio di corrente
Determinazione del guadagno di modo comune
Assumendo
 1

v b3 = −i1 
// rπ 3 // ro3 // rπ 4 
 g m3

vicm
i1 ≈ i2 ≈
2 REE
e
vo = −(g m 4 vb3 − i2 )ro 4
nell’ipotesi di transistori uguali nello
specchio, si ottiene
2
r
rπ 3
r
Acm ≈ − o 4
≈ − o4
2 REE g m3 + 2
β 3 REE
rπ 3
ed infine
G. Martines
Ad
β 3 REE
CMRR =
≈ g m 2 (ro 2 // ro 4 )
Acm
ro 4
20
Coppia differenziale a BJT con carico attivo a specchio di corrente
Tensione di offset determinata dallo schema non simmetrico
Dalla dissimmetria e dall’errore nello
specchio di corrente nasce una tensione di
offset. Infatti:
2
αI
αI β P
∆i =
≈
2
2
βP
1+
βP
e quindi
VOS = −
G. Martines
αI β P
2V
∆i
=−
=− T
Gm
αI 2VT
βP
21
Coppia differenziale MOS con carico passivo
G. Martines
22
Coppia differenziale MOS con carico passivo
Funzionamento con segnale di modo comune
I
vCM max = Vt + VDD − RD
2
vCM min = −VSS + VCS + Vt + VOV
con VCS tensione minima per il
corretto funzionamento del
generatore.
Nota: VOV rappresenta la
tensione di overdrive cioè
VOV = VGS − Vt
G. Martines
23
Transcaratteristica della coppia differenziale MOS
In modo analogo a
quanto già visto per
la coppia con BJT, si
può dimostrare che
I vid
id =
VOV 2
vid
per 2 << VOV
G. Martines
24
Transcaratteristica della coppia differenziale MOS
Il campo di linearità può essere aumentato aumentando la VOV ma questo implica
aumentare I e quindi diminuire il fattore di amplificazione µf ed il guadagno di tensione.
Per il resto, la trattazione è analoga a quella già vista per la coppia con BJT.
G. Martines
25
Coppia differenziale CMOS con specchio di corrente
Le principali equazioni:
RO = ro 2 // ro 4
Ad = g m 2 (ro 2 // ro 4 )
g m ro µ f
Nell’ipotesi ro 2 = ro 4 si ha Ad = 2 = 2 .
Nell’ipotesi ro3 = ro 4 e g m3 ro3 >> 1 :
1
Acm ≈ −
2 g m3 RSS
CMRR = g m 2 (ro 2 // ro 4 )2 g m3 RSS
G. Martines
26
Risposta in frequenza della coppia differenziale
Per questa analisi si fa
riferimento ai due circuiti
equivalenti per il segnale
differenziale e di modo comune
G. Martines
27
Risposta in frequenza della coppia differenziale
Risposta per il segnale differenziale
C IN
G. Martines
Ad = g m (ro // RD )
1
fH =
2πC IN RS
= C gs + C gd [1+ g m (ro // RD )]
Risposta per il segnale di modo comune
 R  ∆R
ACM = − D  D
 2 RSS  RD
1
fZ =
2πC SS RSS
28
Risposta in frequenza della coppia differenziale
Risposta in frequenza del rapporto di reiezione di modo comune
G. Martines
29
Configurazione Darlington
G. Martines
30
Configurazione Cascode
G. Martines
31
Configurazione Cascode con BJT
G. Martines
32
G. Martines
33
G. Martines
34
Coppia differenziale con BJT in configurazione cascode
G. Martines
35